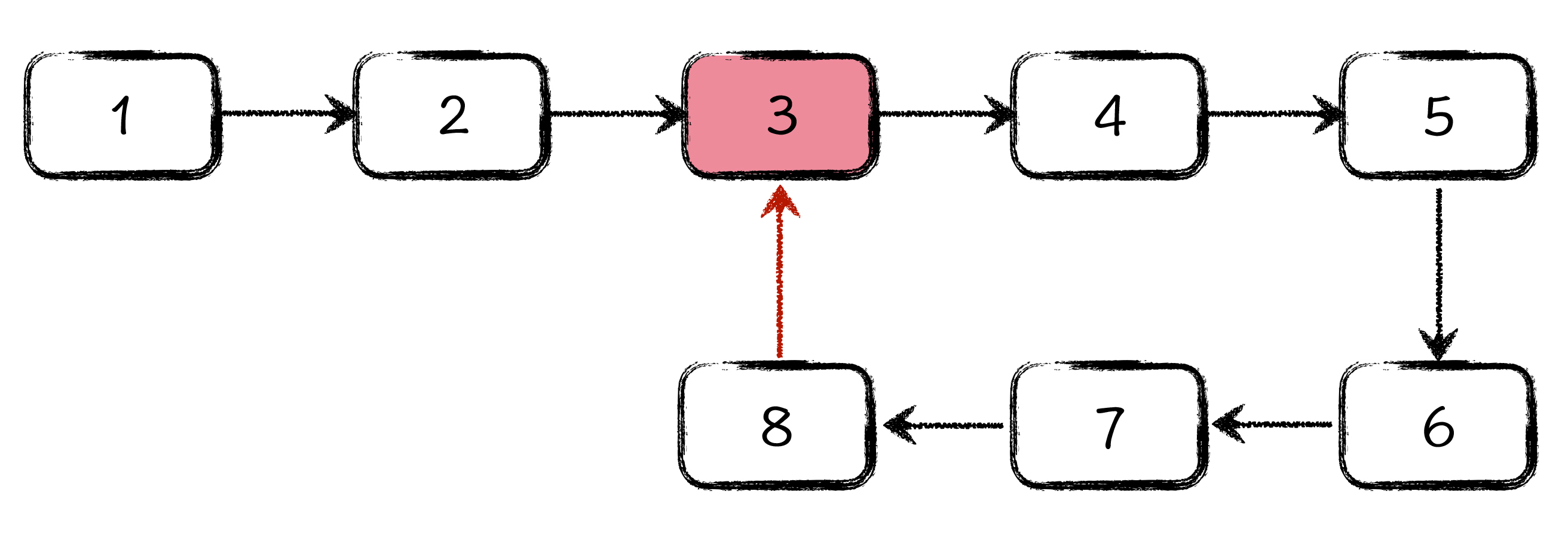
就如你所看到的,图中的8号节点,本应该是链表的最后一个节点,可它却指向了3号节点,这样就形成了一个以3、4、5、6、7、8号节点为循环状态的环形结构。当你使用指针遍历这个链表的时候,将会永无尽头。
你好,我是胡光,欢迎回来。
上节课,我们着重介绍了数据结构的学习方法,就是把数据结构分成两部分进行学习:结构定义和结构操作。其中,结构定义是定义数据结构的样子和性质,结构操作就是数据结构的相关功能,并且在操作过程中需要维护相关结构的性质。在这个基础上,我们详细讲了链表的基础结构。
我们经常听到,算法中最有价值的是“算法思维”,其实在数据结构中,最有价值的也是“数据结构思维”。今天呢,我们就看看链表这种具体的数据结构,如何变成一种思维层面的数据结构,辅助我们进行思考。
先来看一下今天这 10 分钟的任务吧。首先,我们定义一种数字名称,叫做“快乐数”。所谓快乐数就是经过有限次变换以后,等于 1 的数字。这个变换规则,给出一个非1的数字a ,把它的位数拎出来,求各个位数的平方和,得到一个数字b,如果数字b不是1,那就对数字b的每一位数再做平方和,得到数字c……经过不停的变换,确定最后能否得到 1。
例如,一开始的数字是19,经过变换规则 $1^2 + 9^2 = 82$,得到数字82;因为不是 1 ,所以接着做变换,就是 $8^2 + 2^2 = 68$,再做一次变换 $6^2 + 8^2 = 100$,最后一次做变换 $1^2 + 0^2 + 0^2 = 1$,得到了 1 以后,停止。
由于从 19 开始,通过有限次变换以后,能够到达数字 1,所以数字 19 是“快乐数”。在这个过程中,你应该明白,后面得到的82、68、100其实也是快乐数。所以今天我们要做的,就是给出一个正整数,你来判断这个数字是否是快乐数。
这个任务的难点,不在于判定哪些数字是快乐数,而在于如何判定一个数字不是快乐数。为什么这么说呢?因为不是快乐数,就说明原数字没有办法通过有限次变换,到达数字 1,那么经过多少次,才算是有限次呢?1 千次,1 万次还是10万次呢?你会发现,很难确定这个转换次数的上限。
你可能已经感觉到了这是一个有趣,但似乎又有点难度的任务。那就请你带着这份好奇和困惑,让我们用链表思维解决它!
先忘了上面这个任务,我们先从几个具体的例子,来学习链表相关的进阶操作。
我要带你学习的第一个链表相关的问题呢,就是如何判断一个链表中有环。链表中为什么会有环呢?通过上一节课的学习,我们知道单向链表的最后一个节点,原本应该指向一个叫做 NULL 的空地址,代表整个链表结束。可你有没有想过,如果链表的最后一个节点,指向的不是一个空地址,而是链表中的一个点,那是不是就形成了链表内部的一个环?如下图所示:

就如你所看到的,图中的8号节点,本应该是链表的最后一个节点,可它却指向了3号节点,这样就形成了一个以3、4、5、6、7、8号节点为循环状态的环形结构。当你使用指针遍历这个链表的时候,将会永无尽头。
那有没有什么办法,能够帮助我们判断在一个单向链表中,是否存在环呢?面对这个问题,你可能想要说,很简单啊,我只需要使用一个数组,记录出现过的节点信息,之后每次遍历到新节点,就判断这个节点是否在数组中有记录。如果有的话,说明链表中有环,如果遍历到了 NULL 地址,那就说明链表中无环。
上面这个方法看似可行,但数组会占用与链表等量的额外存储空间,并且效率太差了。假设链表有 n 个节点,当你经过第 1 个节点的时候,你需要在数组中查找 0 次;第 2 个节点的时候,需要在数组中查找 1 次;第 3 个节点需要查找 2 次。
依次类推,第 i 个节点,你需要在数组中查找 i - 1 次,可直到你遍历到第 n + 1个节点的时候,才会发现有重复。此时在数组中查找的总次数将会是 (n + 1) * n / 2 次,接近于 $n^2$ 次,这种时间复杂度,写作 $O(n^2)$。关于时间复杂度,简单来理解,它反映的其实是问题规模与运算次数之间的关系。
接下来呢,我们来假设一种场景,在操场上有两个运动员从跑道起点出发跑步,一个速度比较快,一个速度比较慢。同时操场的能见度特别低,他们根本不知道跑道是不是环形的,可过了一段时间以后,两个人就确定了这个跑道是否环形,他俩是怎么做到的?
你稍微想一想,就会明白这里面的道理:如果跑道是环形的,那么速度快的运动员,在足够的时间里,终究会从速度慢的人后面追上来了,形成两人相遇的情况。如果跑到不是环形的,那速度快的运动员会最先跑到终点,两人不会相遇!这就是今天我们要讲的链表判环的方法,叫做:快慢指针法。
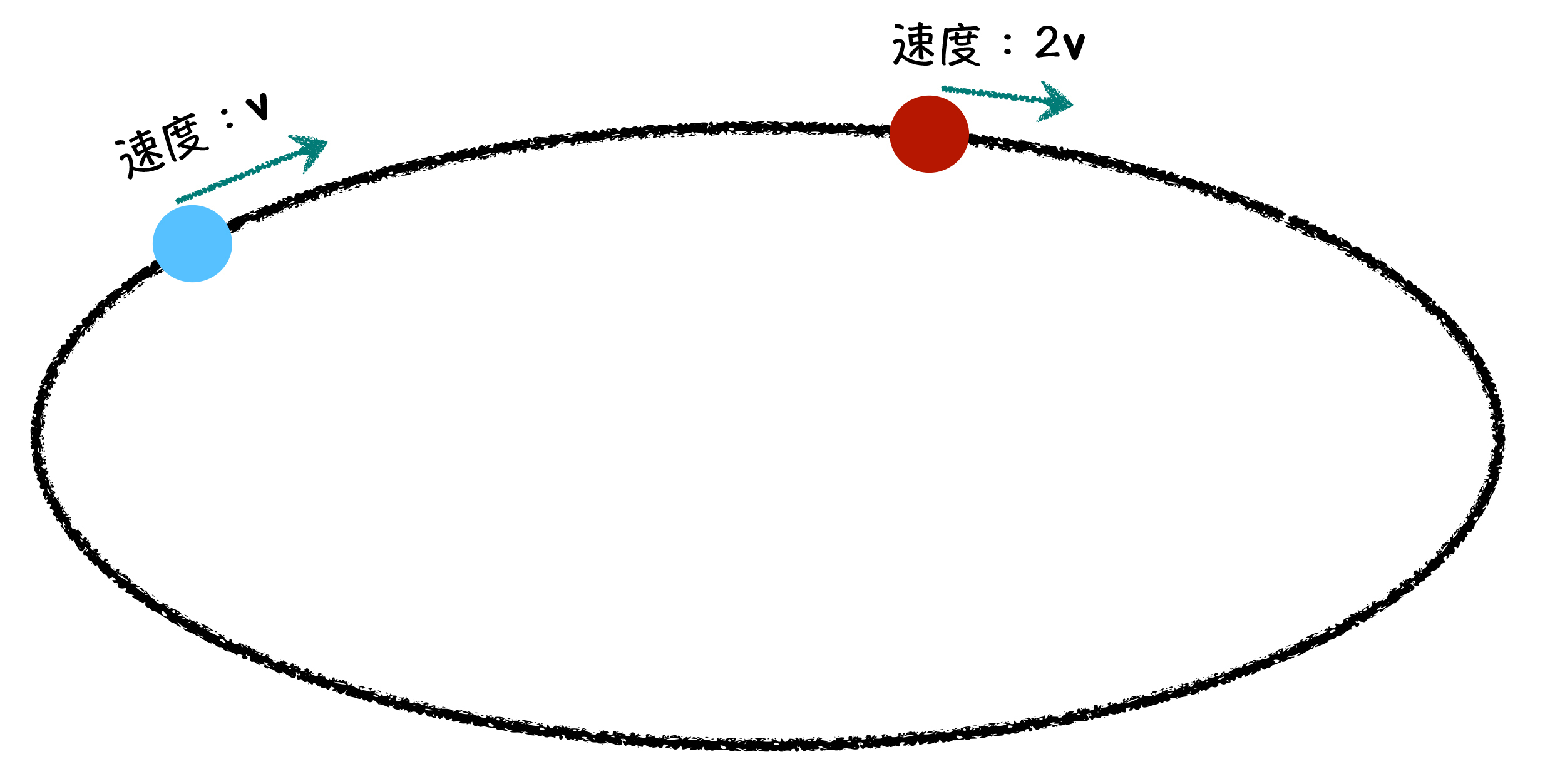
简单来说,就是我们把链表当成跑道,放上两个指针,一个指针每次走一步,另一个指针每次走两步,如果快的指针,先跑到了终点,说明链表中没有环,如果两个指针相遇了,则说明链表中有环。并且,我们很容易知道两个指针一定是在环内部相遇的。
如果把上述过程写成代码的话,如下所示:
int hasCycle(struct Node *head) {
if (head == NULL) return 0;
// p 是慢指针,q 是快指针
struct Node *p = head, *q = head;
// 每次循环,p 走1步,q 走2步
do {
p = p->next;
q = q->next;
if (q == NULL) return 0;
q = q->next;
} while (p != q && q);
return p == q;
}
代码比较简单,你可以自行阅读并学习。其中需要注意的是几个指针判空的语句,一定要保证指针非空的前提下,再用指针间接访问结构体字段,否则你的程序会瞬间崩溃。
前面讲了,如何判断链表有环。那么今天的“一起动手,搞事情”环节呢,我就给你留两个相关的子问题:
准备完了前面这些基础知识以后,你可能还是摸不着头绪,不知道如何解决快乐数判定问题。那你可要跟住节奏了,下面就要进入将链表数据结构提升成为思维的阶段了。
首先,我们知道,整型表示的最大值是${2}^{31} - 1$,大约是 20 亿左右。如果就在这个整型范围内解决快乐数判定的问题,我们可以得到哪些有用的结论呢?下面,让我们分析一下。
由本节开头的例子可知,从19开始,依次得到的是:82、68、100、1这些数字。也就是说,从一个数字开始,按照快乐数的计算规则,会得到一串数字序列。这其中就蕴含着链表重要的结构思维:从当前节点,唯一映射到下一个节点。快乐数序列中的数字,就是链表中的节点,如果当前数字确定了,下一个数字也就是确定了的,就像数字19,下一个肯定是数字82,这种映射规则,就是链表节点之间的指向关系。
最后,我们做一个思维映射,一切就豁然开朗了。所谓快乐数序列,最终的目标是能到 1,这个数字 1,其实就可以看成是链表中的空地址。这样,我们就把快乐数问题,用链表思维做了一番改造,并且这种改造,一点儿违和感都没有。当你把这个思考过程搞清楚后,恭喜你,在这个过程中,你正在将你自己看待问题的方式,变得更加结构化,更加计算机化。
接下来我们分析一下,这个快乐数链表,最长能有多长?这个问题其实比较好分析,主要是思考究竟哪个数字,按照快乐数的计算规则,得到的下一个数字是最大的,这个最大的数字是多少。
稍加思索,你就知道,如果在整型范围内解决快乐数问题的话,1999999999 这个数字,按照各位平方和来进行计算,得到的下一个数字应该是 $(9*9^2 + 1) = 730$,也就是说,这个快乐数链表中,节点数量绝对不会超过 731 个。一个不超过 731 个节点的链表,还总也走不到末尾,说明什么?说明这个链表中有环!
至此,你会发现,判断一个数字是否是快乐数,等价于判断链表中是否有环。剩下的台词,我就不和你抢了,舞台留给你来发挥吧,代码我就不替你写了。加油!我相信,你一定写得出来。
关于链表的内容,到这里就结束了。通过这两节,只是想让你记住一点:数据结构,不仅仅是计算机中的代码,更是我们思维的逻辑结构在计算机科学中的具体体现。
这种有趣的思维变换,才是算法和数据结构的真正魅力所在。有些技术的酷炫,是长在脸上的,让人一眼就能看到;而算法和数据结构的酷炫,从来都是那样的含蓄,那样的内敛,你只有深入到里面,才能感受到它的巨大魅力。我已经竭尽所能,试图将它的内在美描述出来,不知道你有没有 get 到,如果你没有 get 到,那一定是我的语言太过苍白,而不是算法数据结构没有魅力!
好了,今天先到这里了,我是胡光,我们下期见。