你好,我是胡光,欢迎回来。
上节课呢,我们学习了二分查找的基本思想,以及明确了二分答案所使用的问题模型,你会发现,正因为问题具有单调性,我们才可以使用二分查找算法对问题求解过程进行加速。
今天呢,我将带你学习一种性质有趣、简单且高效的数据结构,叫做:单调队列。学习这个数据结构的时候呢,我们还是要强调一下那句话:数据结构,就是定义一种性质,并且维护这种性质。
在正式开始学习之前呢,先来看一下今天这 10 分钟的任务吧。
滑动区间最大值,就是指在固定区间长度的前提下,在一个序列上,从前到后滑动这个区间窗口,每次窗口内部的最大值,就组成了滑动区间最大值。
例如,给你如下包含 8 个数字的序列,区间长度设置为 3:
[6 4 2] 10 3 8 5 9 -> 6
6 [4 2 10] 3 8 5 9 -> 10
6 4 [2 10 3] 8 5 9 -> 10
6 4 2 [10 3 8] 5 9 -> 10
6 4 2 10 [3 8 5] 9 -> 8
6 4 2 10 3 [8 5 9] -> 9
滑动区间从数字6开始出发,每次向右移动一个数字,同时把左边的一个数字丢出去,保持区间长度为3,最后移动到数字9停止。可以看到,这个序列共包含8个数字,所以最后形成的滑动区间最大值共有6个,依次是 6、10、10、10、8、9。
面对这个问题,你很容易采用 $O(nm)$ 的算法来完成,n 是区间长度,m 是窗口长度,就是枚举区间的终止位置,每次扫描区间内部,获得最大值。
而我今天要给你讲的这种方法,能让时间复杂度降低到 $O(n)$,你可以认为是对原序列扫描一遍,就能得到问题的答案。这究竟是什么样神奇的方法呢?带着这份好奇,我们开始今天的课程吧!
想要完成今天这个任务呢,你必须掌握今天我将要教给你的一种新的结构,就是:单调队列。
首先让我们来认识一下最简单的队列结构,举一个生活中最常见的例子:火车站排队买票,你应该都经历过吧?售票员坐在窗口里面,每次只能服务队列中排在最前面的那个人,每当有人买完票,都会从队列的头部离开,后面的人上前一步,接替离开的人向售票员购票,当有其他人想要来买票的时候,必须从队列的末尾开始排队。这种结构就是典型的队列结构。
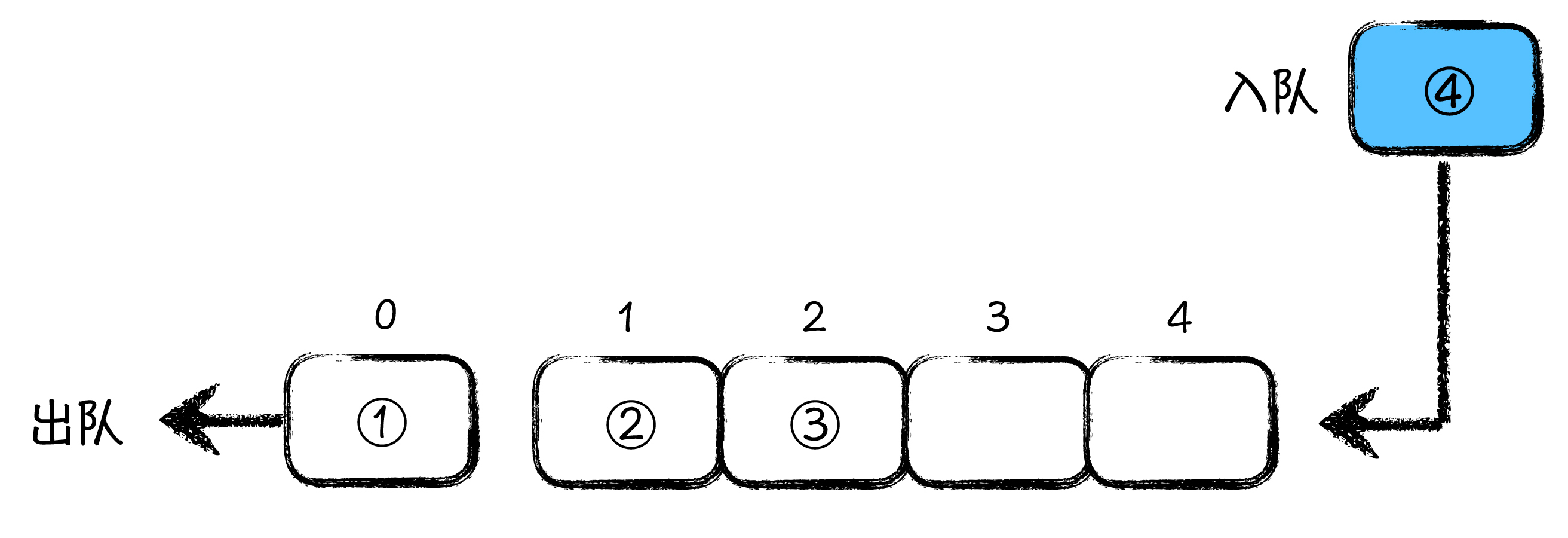
我们计算机中的队列,和买票的这个队列是一样的,先到先得,先入先出,每个元素都是从队列尾部入队,在头部被处理完后再出队。如下图所示:

如图所示,队列就像一个数组一样,每个元素从数组尾部进入数组,从头部出数组。这种结构很简单,你应该很容易理解它的工作顺序。任何事物,往往就是看起来越简单,想要掌握其真谛就越难。就像是我给你一把锤子,你知道这东西大概可以干什么,而我要是给你一块铁,你可能就懵了。其实队列就是这种表面简单,可作用却不简单的数据结构。
想要理解队列,你就必须理解一句话,叫做:计算机是很专注的。什么意思呢,我们回忆一下之前讲到的链表判环,作为人类的你和我,可以一眼就看出来链表中是否有环。而对于计算机程序来说,只有指针指向的地方,才是它能看得到的地方。所以,我们才费了很大的力气,为计算机设计了一个快慢指针的算法,来判断链表中是否有环。
实际上,当我们在实现程序的时候,我们不仅要把数据存储在计算机中,我们还要规定计算机处理这些数据的顺序。想一想,我们之前设计的所有的循环程序,不就是在规定计算机的处理顺序么?
而今天我们学习的这个队列,你可以把其中的元素,看成是计算机要处理的一个个的任务,那么队列结构,其实就是规定了这些任务的处理顺序,程序只从队列头部取任务,先到先处理,后到的任务,需要在队列后面排着,直到轮到它,这样就可以把计算机的专注与高效发挥到极致。
学习编程,与其说是将我们的思维转换成代码,不如说是将我们的思维,锻炼成计算机的思维。注意,计算机的处理逻辑,是有顺序的。今天,我们所说的队列,就代表了一种顺序。后面,我们还会介绍另外一种顺序的代表,就是“栈”,到时候我再详细讲解。
讲完了最简单的队列以后,下面就来让我们学习一种队列的升级产物:单调队列。在正式讲解单调队列之前,让我们来讲一个现实中的单调队列的例子。
假设你的学长张三,作为乒乓球体育生,很幸运地进了高中学校的校队。学校规定当前校队中,能力最强的人,才有可能代表学校去参加比赛。那么在校的这三年,张三都有机会代表学校参加国家赛。
高一的时候张三战斗力 85,比他能力强的有两个人,一个是高二的孔令辉,战斗力 93,一个是高三的刘国梁,战斗力 98。那么此时,能代表学校参加比赛的只有最高战力的刘国梁。

过了一年,张三上了高二,原高二的孔令辉上了高三,刘国梁毕业了,如果张三的战力比后面上来的新生要强,那么他再等一年,有可能在高三的时候代表学校参赛。然而这时作为高一乒乓球体育生的你也进入了校队,战斗力 88。悲剧出现了,因为只要你在学校,张三永远不可能参加国家赛了。

这个时候你欣喜若狂,因为再熬一年,如果新学弟战斗力没你高的话,你就能代表学校去参加国家赛了。很快一年又过去了,你终于熬到了高二,同时也迎来了一名新学弟张继科,战斗力 90。悲剧再次上演,你和张三一样,也失去了代表学校参赛的机会了,此时你的心情,是不是五味杂陈?

上面的几个校队名单呢,就是我们所谓的单调队列,如果把学生从高年级到低年级排列,随着时间的流逝,这本身就是一个队列结构,高年级的同学从队列头部毕业,低年级的同学从队列尾部进入。
而这个校队名单,记录的是最有可能代表学校参加比赛队员的名字。刘国梁毕业了,最有可能接班的是孔令辉,孔令辉毕业了,最有可能接班的是张三。而当你进入队列的那一刻,张三尽管比你入队早,但战力没你高,所以张三就永远失去了机会。后来张继科进入队列,你遭遇了和张三一样的悲剧。
如果你要是仔细观察校队名单,你会发现校队名单上,永远是按照能力值的从高到低,来记录学校里面的种子选手。这个名单,既有队列的样子,又有单调的性质,所以称为“单调队列”。
单调队列的作用,就是用来维护在队列处理顺序中的区间最大值。就像上面所说的校队名单,维护的就是区间长度为3时候的最大值。当一个新的元素入队的时候,它会把其前面违反单调性的元素,都从队列中踢掉,就像张继科的入学,把你踢出了校队名单,最终他成为了队列里的最大值。
让我们回到开始的求“滑动窗口最大值”的任务。其实,滑动窗口每次向后滑动一位,会有一个元素从队首出队,同时也会有一个元素从队尾入队,所以滑动窗口的过程,就遵照了我们所谓的队列处理顺序。
而这个任务,本身就是求区间最大值的,所以也符合了单调队列应用的场景:维护在队列处理顺序中的区间最大值。下面呢,我们就来看一下具体代码:
#define MAX_N 1000
int q[MAX_N + 5], head, tail;
void interval_max_number(int *a, int n, int m) {
head = tail = 0;
for (int i = 0; i < n; i++) {
// a[i] 入队,将违反单调性的从队列 q 中踢出
while (head < tail && a[q[tail - 1]] < a[i]) tail--;
q[tail++] = i; // i 入队
// 判断队列头部元素是否出了窗口范围
if (i - m == q[head]) head++;
// 输出区间内最大值
if (i + 1 >= m) {
printf("interval(%d, %d)", i - m + 1, i);
printf(" = %d\n", a[q[head]]);
}
}
return ;
}
如代码所示,interval_max_number 函数,传入三个参数,数组首地址 a,元素数量 n 以及 区间长度 m。代码中的 q 数组,后续的作用就是模拟单调队列,head 与 tail 代表了队列的头尾下标,这里我们采用左闭右开式的表示方法,也就是 head 和 tail 所指示的区间范围内,包含 head 所指位置,但不包含 tail 所指位置。
函数内部,依次处理数组中的每个元素,每次处理相应元素的时候,涉及到两个过程:
这样我们就可以保证,我们每次输出的,就都是滑动窗口内部的区间最大值了。
以上就是我们今天要学习的单调队列的内容,关于单调队列的知识,你在理解其处理过程的时候,更应该记住单调队列应用的场景:就是维护队列处理顺序中的区间最大值。
这个里面,需要重点强调一个队列处理顺序 。也就是说,如果你可以把一个问题的求解顺序,抽象成队列求解顺序,并且在这个过程中,你还需要维护区间最大值,那么翻出“单调队列”,准能帮助你大幅度提升处理速度!而单调队列,无论是入队,还是出队,操作完以后,一定要保证队列内部满足单调性,这就是开头我们说的:定义一种性质,并且维护这种性质。单调队列,维护的就是单调性。
最后,我们来简单说一下单调队列处理单个元素的平均时间复杂度为什么是 $O(1)$ 的。假设我们要处理 n 个元素,从整体上来看,每个元素会入队列 1 次,出队列最多也是 1 次,那么n 个元素的总操作次数不会超过 $2 \times n$ 次,平均到一个元素上就是 2 次,也就是常数次,记作 $O(1)$ 时间复杂度。由此得知,处理 n 个元素的总时间复杂度,就是 $O(n)$。
今天没有思考题,因为这节课的内容只是作为一个铺垫,下节课关于“栈”的知识才是重头戏。我也希望你对这节课的内容认真学习体会,可以的话,在留言区说说你的看法和思考。
好了,单调队列的知识,就讲到这里了,我是胡光,我们下期见。