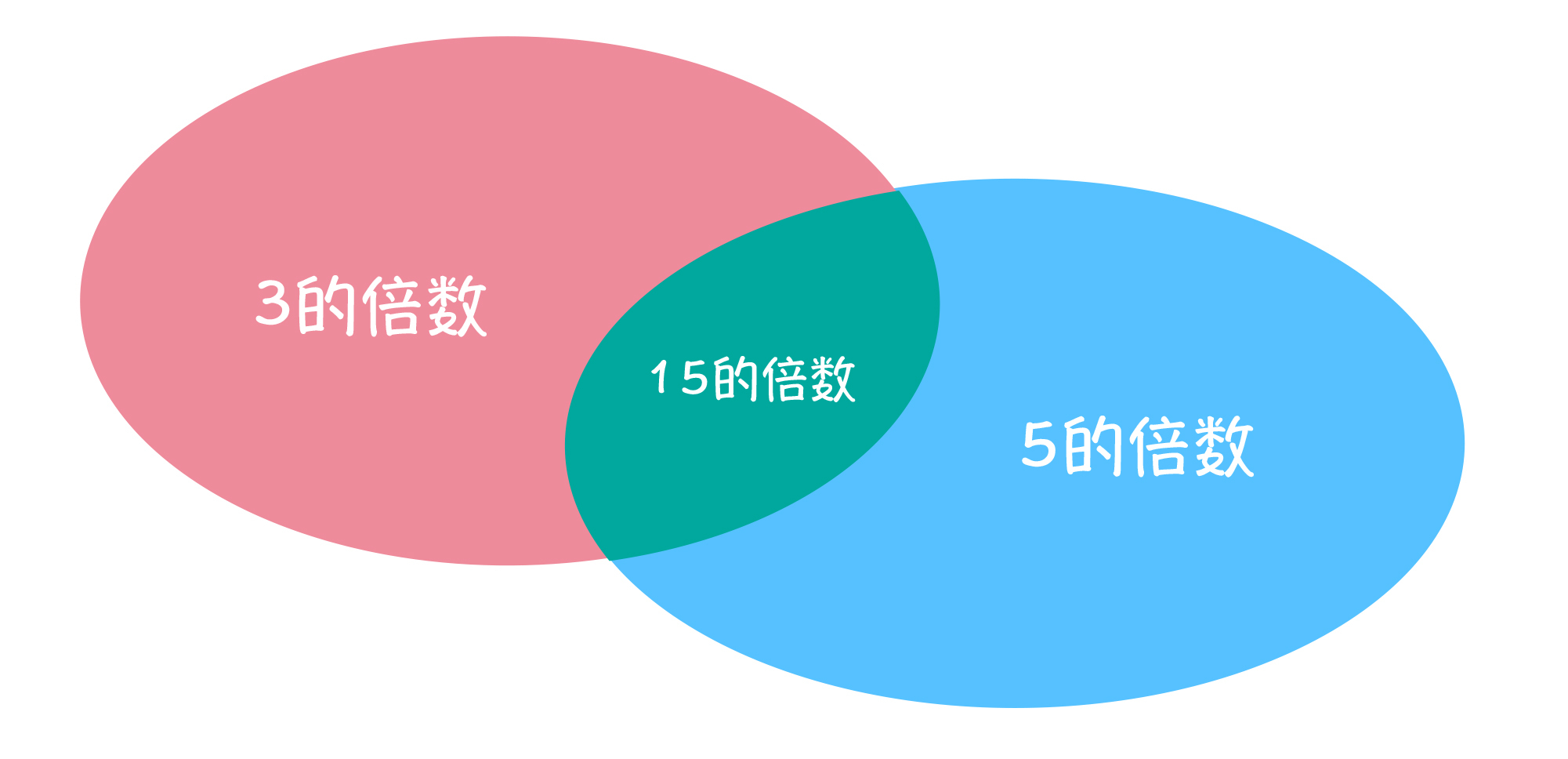
当时,我们提出了基于等差数列求和的一种做法,就是用 3 的倍数,加上 5 的倍数,然而我们发现,有一部分加多了,就又减掉了 15 的倍数,这样才是我们真正想要求的值。你仔细想一想,这种做法本质上,其实就是容斥原理的一种体现。
你好,我是胡光,欢迎回来。
上两节呢,我们学习了两个具有单调性的数据结构:单调队列和单调栈。其中,单调队列是用来维护滑动窗口内的区间最值的单调结构,单调栈是用来维护最近大于或小于关系的单调结构。这两种单调结构的均摊时间复杂度都是 $O(1)$,每个元素的操作次数最多是 2 次,足以看到这两种结构的高效。如果想彻底掌握这两种结构,我建议你在课下时间不断地练习。
从今天开始呢,我们将从数据结构,跳跃到算法的学习上。将要带你认识一类比较偏重于思维的算法,大类叫做递推算法,以及其中的一个重要的组成部分,动态规划类算法。
关于递推算法,在“语言基础篇”的第05讲《数组:一秒钟,定义1000个变量》中,我们其实就使用了递推算法的思想。如果你已经忘了的话,我建议你可以先回去看看,复习一下之前的内容,为今天的课程做好充足的准备。
咱们今天这10分钟的任务呢,和钱有关系。众所周知,在不计算小于 1 元钱的面额的前提下,我国的纸币系统中,曾经拥有如下面值:1元、2元、5元、10元、20元、50元 和 100元。假设,每一种面值的纸币,我们都有无限张,现在想用这些钱凑出1000元,请问你有多少种不同的方案?
这里说的不同方案,是不关注钱币之间的顺序的,例如要凑 7 元钱,可以是1元、5元、1元,也可以是1元、1元、5元,这两种方案我们视为同一种。
好了,面对这个问题,你要怎么解决呢?让我们开始今天的学习吧。
在讲今天的递推问题之前呢,先来和你解释一个与递推思维相关的数学原理:容斥原理。
我们知道,一般在计数问题中,为了保证计数准确,必须注意两个事情:一是没有重复,二是没有遗漏。保证没有遗漏,这一点比较好做到,就像对某片地区采取地毯式轰炸,只要炸弹足够多,你可以很容易地保证,没有任何一个被漏掉的地方。可你要保证任何一片土地都仅被轰炸一次,这就很难做到。计数类问题往往也是这样的,想要保证没有遗漏的计数,比较简单,可要是想保证没有重复的计数,可能就困难那么一点儿了。
容斥原理就是为了解决计数类问题中的重复问题,其基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排除出去,使得计算的结果既无遗漏又无重复。简单来说,就是在计算过程中,如果加多了,就把加多的部分减掉,如果发现又减多了,就再加回来一部分,一直到不多不少为止。
这么说,你可能还是有点儿懵。没关系,回想一下,我们之前在第13节课《程序设计原则:把计算过程交给计算机》中,提到的求1000以内,3或者5倍数的所有数字和的问题。
原问题解决方法如图所示:

当时,我们提出了基于等差数列求和的一种做法,就是用 3 的倍数,加上 5 的倍数,然而我们发现,有一部分加多了,就又减掉了 15 的倍数,这样才是我们真正想要求的值。你仔细想一想,这种做法本质上,其实就是容斥原理的一种体现。
关于理解容斥原理,你需要理解问题的集合思维,关于这点呢,我在下面还会带着你做详细的解释。
我们先从一个简单的问题开始,逐步熟悉容斥原理与递推算法。假设在一片草原上,莫名其妙来了一只外星兔子,这种外星兔子呢,第一个月的时候是幼体,第二个月成长为成体,从第三个月开始,成体兔子每个月都会产生出一只克隆体的幼体兔子,而且这种兔子不会衰老,一旦成体以后,就会一直生下去。按照这种情况,请你计算出第 n 个月,草原上有多少只兔子?
这里我给出了前6个月,草原上兔子数量的情况:
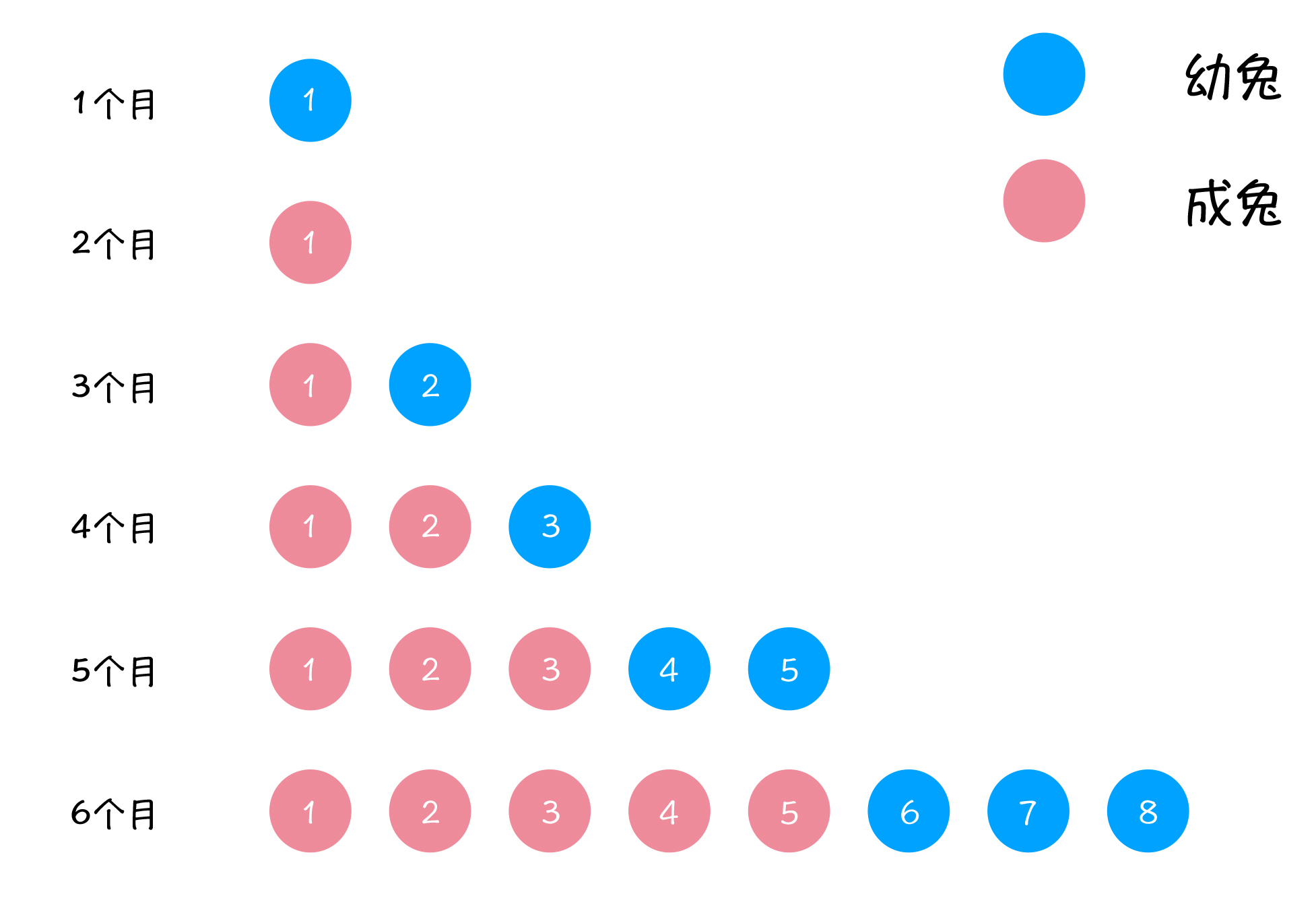
我们看到,从第1个月到第6个月,草原上兔子的数量分别是:1、1、2、3、5、8,我们主要来分析第6个月兔子的组成情况。
第6个月共有 8 只兔子,其中5 只成兔,3 只幼兔。可以看到,之所以有 5 只成兔,是因为上个月总共有5只兔子,毕竟根据兔子的成长周期,不管它们是否成年,到下个月都会成长为成兔,所以第6个月的成兔数量等于第5个月的兔子总数。
而第6个月的另外的3 只幼兔,是由第 5 个月的 3 只成兔产生的,根据前面的推论,我们知道第5个月的3只成兔,是源自第4个月的兔子总数。所以,第6个月的幼兔数量等于第4个月的兔子总数。
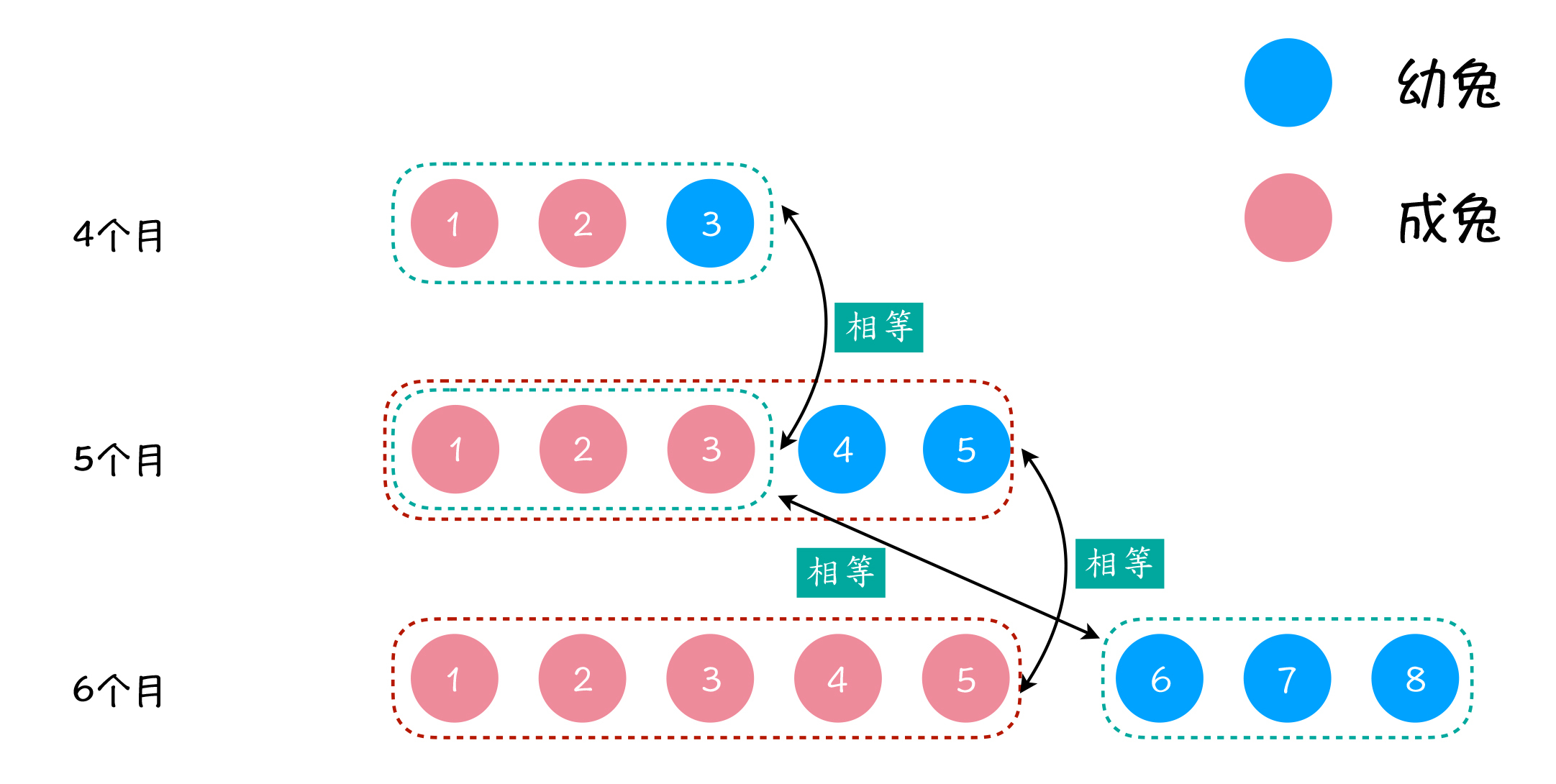
因此,我们可以得出这样的一个结论:从第3个月开始,第 n 个月的兔子总数,等于该月的成兔数量与幼兔数量之和,也就等于第 n - 1 个月的兔子数量与第n - 2个月的兔子数量之和。
在这个兔子繁殖问题中,我们把当前月份的兔子分成两类,一类是成年兔子,一类是幼年兔子。这种分类方法,就保证了我们对两类分别统计的时候,它们之间没有交集,也就不需要考虑容斥原理中剔除重复部分的过程了。
之后,我们重点分析本月的成年兔子数量、幼年兔子数量与之前的哪个量有关系,最终得到了一个只使用某个月兔子数量,对本月兔子数量进行表示的数学关系。这种使用序列中的前项的值,来计算当前项值的做法,就是我们今天要讲的递推算法。
那么这个算法具体如何求解呢?下面我们就来看看递推问题的求解过程。
递推问题,通常分成三步进行求解。第一步,确定递推状态,也叫做状态定义;第二步,推导递推公式;最后一步,程序设计与编写。
接下来,我将用前面的兔子繁殖问题为例,说明递推问题求解的前两个步骤。最后一步的程序设计与编写,将作为作业题,留给你来完成。
所谓确定递推状态,就是确定一个有明确含义的数学符号,这里重要的是这个明确含义,而非那个数学符号。
什么意思呢?就以兔子繁殖问题为例,当我们分析完问题以后,就可以定义出具有明确语义的数学符号,例如:f(n) 。如果我们仅仅列出这么一个数学符号,其实是没有多大意义的,可是当我们定义了它的语义,即 f(n) 代表第 n 个月兔子的数量,这才算是完成了状态定义。因为只有确定了状态定义,我们才能进行下一步的递推公式推导。
说到这里,在继续讲下面递推公式推导之前,你可能会有疑问了:这个状态定义中的数学符号虽然不重要,可一般是怎么确定出来的呢?
针对这类问题,那就不得不提到我的思考技巧了:我一般会把递推类问题,看成是初中的代数问题,先分析问题中的自变量和因变量。自变量,就是问题中那些不受控制的量,就像兔子繁殖问题中的月份。而因变量就是那些随自变量改变而改变的量,就像兔子繁殖问题中兔子的数量,是随着月份而改变的。
所以,我的技巧就是把和问题求解量相关的自变量,都作为数学符号中的参数,然后将相关问题求解量作为数学符号映射值的含义。就像我们刚刚所说的,f(n) 代表第 n 个月兔子的数量,在这个状态定义中,将问题求解量,也就是兔子数量,作为函数映射值的含义;而与问题求解量,即兔子数量相关的自变量只有一个,那就是月份,所以我们将月份作为函数的参数。
这样,我们就完成了状态定义。
接下来,就是递推问题求解的第二步了,推导递推公式。在推导递推公式的时候,这里需要用到前面我们定义的递推状态,并且,使用时一定要严格遵守递推状态的语义信息。
例如,在兔子繁殖问题中,如果你想用状态 f(n) 做公式推导的时候,那么 f(n - 1) 就代表了第 n - 1 个月兔子的数量,而 f(n - 2) 就代表第 n - 2 个月兔子的数量。这就是我刚刚所说的“要严格遵守递推状态的语义信息”的意思。
一般做递推公式推导的时候,我们主要思考的事情是,当前递推状态和前几项递推状态之间的关系。例如,在兔子繁殖问题中,当我们确定了递推状态 f(n) 以后,通过分析可以得到如下递推公式:
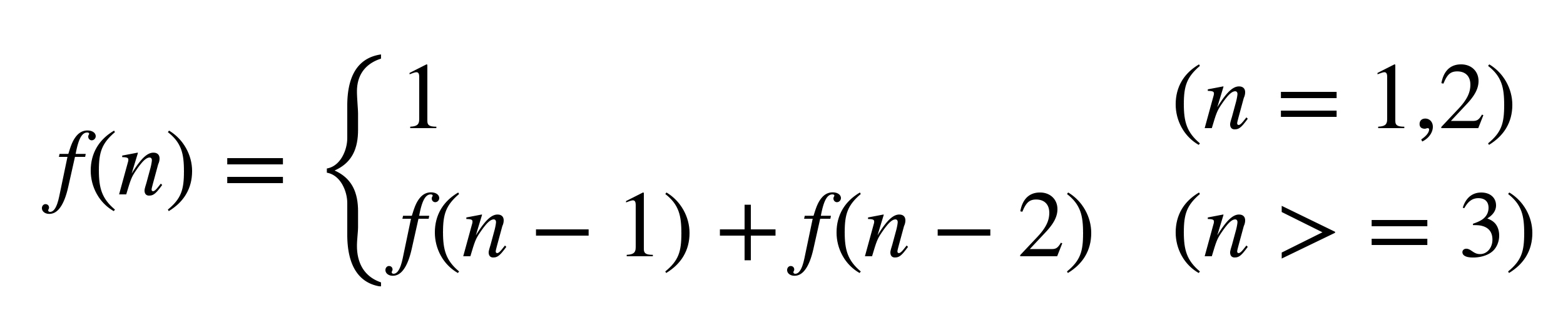
根据前面对兔子繁殖问题的分析,你应该很容易理解这个递推公式吧?就是前两个月(n=1,2),兔子的数量都是1只;到第三个月以及之后的月份(n>=3),本月的兔子数量等于上两个月的兔子数量之和。其中 f(n - 1) 等于本月中成兔的数量,f(n - 2) 实际代表的是 2 个月前的兔子数量,它也等于本月中幼兔的数量。套用集合的思想就是,成兔与幼兔这两部分互为补集,加在一起就正好等于全集。
细心的你肯定发现了,这个公式是不是在哪里见过?没错,在咱们的第12节课《数学归纳法:搞定循环与递归的钥匙》中,我们提到了菲波那契数列递推公式,就跟这个兔子繁殖公式一模一样。
请你来完成兔子繁殖问题的第三步:程序设计与编写。要求是用两种方式完成:
在你用递归实现了兔子繁殖问题的求解过程以后,我希望你可以计算下80个月后,兔子的数量。你的程序将发生一些奇奇怪怪的现象,试着自己去理解这个程序现象,并且想一想,如何解决出现的问题吧。
在这里呢,再跟你多说一句,在进行程序实践的时候,一定要注意总结我们之前讲过的数学归纳法和递推算法与程序之间的关系。
最后,让我们回到今天的任务,也就是用1元、2元、5元、10元、20元、50元和100元凑成1000元钱,总共有多少种方案。
第一步,让我们来确定递推状态。确定递推状态之前,我们需要分析清楚题目中的自变量与因变量。因变量比较好分析,就是方案总数,那这个方案总数都受什么影响呢?很明显,是钱币的种类和拼凑目标金额。也就是说,钱币种类发生变化,方案总数就会发生变化;同理,如果拼凑的目标金额发生变化,方案总数也一定会发生变化。所以,自变量是 2 个,钱币种类和拼凑的钱币数量。因变量是 1 个,就是方案总数。
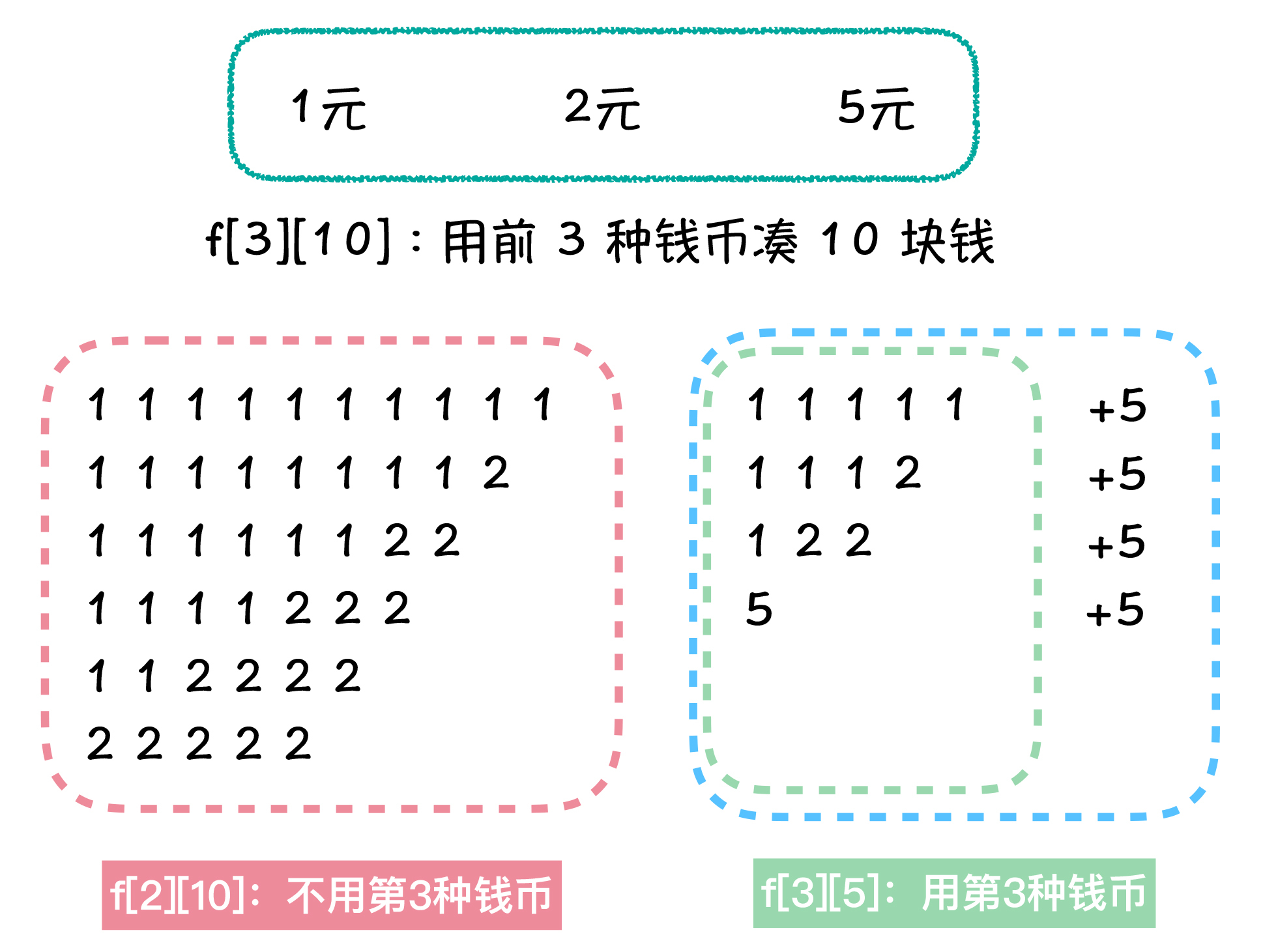
通过上面的分析,我们就可以列出状态定义:f(i, j) ,代表使用前 i 种钱币,拼凑 j 元钱的方案总数。例如,f[3][10] 就代表使用前3种钱币,也就是只使用1元、2元、5元,凑10元钱的方案总数。
第二步,就是用这个状态定义,进行递推公式推导,关键就是分析当前项与前几项的关系。核心思想其实就是容斥原理,也就是用某几项表示 f(i, j) ,如果发现这些表示 f(i, j) 的项之间存在交集,就将交集部分减去,如果减多了再加回来一些,直到正好表示 f(i, j) 为止。
好在这道题目还算是一道简单的递推问题,我们可以将 f(i, j) 划分成性质不同且互为补集的两部分。在 f(i, j) 所代表的所有方案中,一部分方案是使用了第 i 种钱币的,另外一部分方案中是没有使用第 i 种钱币的,我们就用这个性质,将 f(i, j) 表示成两项相加之和的形式。
例如,在用前三种钱币,拼凑 10 元钱的所有方案中,可以按照方案中是否使用第 3 种钱币,也就是是否使用了 5 元钱,将所有方案划分成两类。
其中一类方案不包含第 3 种钱币,也就是不用 5 元这个钱币,这些方案的数量,等价于使用前 2 种钱币拼凑 10 元钱的方案总数,也就是 f[2][10] 的值。另外一类方案中,使用了至少 1 张 5 块钱,那么我们可以在这些方案中,都拿掉一张 5 元钱,剩余的部分组成的方案数量,就等于 f[3][5],也就是用前 3 种钱币凑 5 元钱的方案总数。
这样我们就推导出了递推公式:f[3][10] = f[2][10] + f[3][5]。
回到我们的任务,就是在 f(i, j) 代表的所有方案中,没有使用第 i 种钱币,拼凑 j 元钱的方案数量,就是 f(i - 1, j),代表使用前 i - 1 种钱币拼凑 j 元钱的方案总数。剩下的使用了第 i 种钱币的方案中,由于都存在第 i 种钱币至少 1 张,假设第 i 种钱币的面额是 val[i],也就意味着,我们可以使用前 i 种钱币,凑 j - val[i] 的钱数,给第 i 种钱币留出一个位置,这么做所对应的方案总数就是 f(i, j - val[i])。
最终,我们推导出了递推公式:f(i, j) = f(i - 1, j) + f(i, j - val[i])。其中,边界条件是 f(1, k * val[1]) = 1,也就是用在只使用第 1 种钱币的条件下,想要凑第 1 种钱币的整数倍面额的方案总数都是 1。
至此,我们就完成了凑钱币问题的递推求解过程。最后,还剩一个程序实现,试着自己完成一下吧,加油!你可以的!
最后呢,我们来总结一下今天的内容,今天的内容主要想让你记住三点:
递推问题的求解过程,不是一朝一夕就能掌握的,今天的课程呢,只是让你拥有这种感觉,以及掌握求解递推问题的重要思考过程。我相信,只要你沿着今天讲的递推问题求解过程,去学习每一个递推问题,总有一天,你会对递推问题理解得更加透彻。
对于学有余力的小伙伴们,如果想更深入地了解一下容斥原理,可以通过学习莫比乌斯函数、狄利克雷卷积与莫比乌斯反演等内容,进一步感受一下这个思想所绽放出的光芒。
好了,关于递推的知识今天就讲到这里了,我是胡光,咱们下期见。
评论