我们把其中的 A 节点叫做“根节点”,B 和 C 是 A 节点的两个“子节点”,同理,E 和 F 是 C 节点的两个子节点,D 是 B 节点的子节点。如果更细致地划分,以 B 为根节点的子树,处于 A 节点的左侧,所以称为 A 节点的左子树,C 称为 A 节点的右子树。反过来,我们把 A 节点称为 B 和 C 节点的父节点,同时它也是 D、E、F 节点的祖先节点。以上就是二叉树中的一些基本概念了。
你好,我是胡光,欢迎来到“综合项目篇”的最后一节课。
这节课,我将带你完成一个富有挑战性的任务,就是一起开发一门“编程语言”。哈哈……我说开发一门编程语言当然是和你开玩笑,不过我们可以开发编程语言中的一小部分,那就是定义变量和基本的表达式运算功能。
三个月的时间,我们一起用 C 语言写了这么久的代码,我相信只要你坚持学习,不断拓展自己的编程能力,终有一天你可以开发出一门自己的编程语言。今天,我就带你打个头阵,从计算器程序开始。
我们将要实现的计算器程序也算是开发一个小项目,那么开发项目的第一步,就是对我们实现的功能进行设计,一般计算器功能如下:
这两个功能,看似简单,可实际要考虑的还很多,例如:变量是否有作用域的限制啊,合法变量名的规则,表达式中支持的运算符种类啊,每一种运算符的优先级,等等。这些需要考虑的细节,每一个都会给我们的项目增加一点点难度。
为了把难度控制在一个可以实现的范围,我们对计算器功能做进一步的细致描述,同时也是降低项目实现难度,重新修订的功能定义如下:
这里,我给你看一份符合上述规则的输入数据:
a = 3
b = a * 3 + 5
(a + 4) * (b + 5)
可以看到,第 1 行输入,定义了变量 a,同时给 a 变量赋值为 3;第 2 行,定义了变量 b,同时给 b 变量赋值为 a * 3 + 5 的值,也就是 14;第 3 行,是一行表达式,计算的是 (a + 4) * (b + 5) 的值,最后的结果应该等于 7 * 19 = 133。
针对这份输入数据,我们的计算器程序分别输出每行表达式对应的值,也就是:
3
14
133
清楚了计算器程序的功能以后,下面我就给你讲讲如何完成这个程序。
首先,你需要掌握二叉树的三种遍历方式,这是我们后续解决表达式求值问题的思维利器。在讲遍历方式之前,先来简单的看一下二叉树的基本结构。
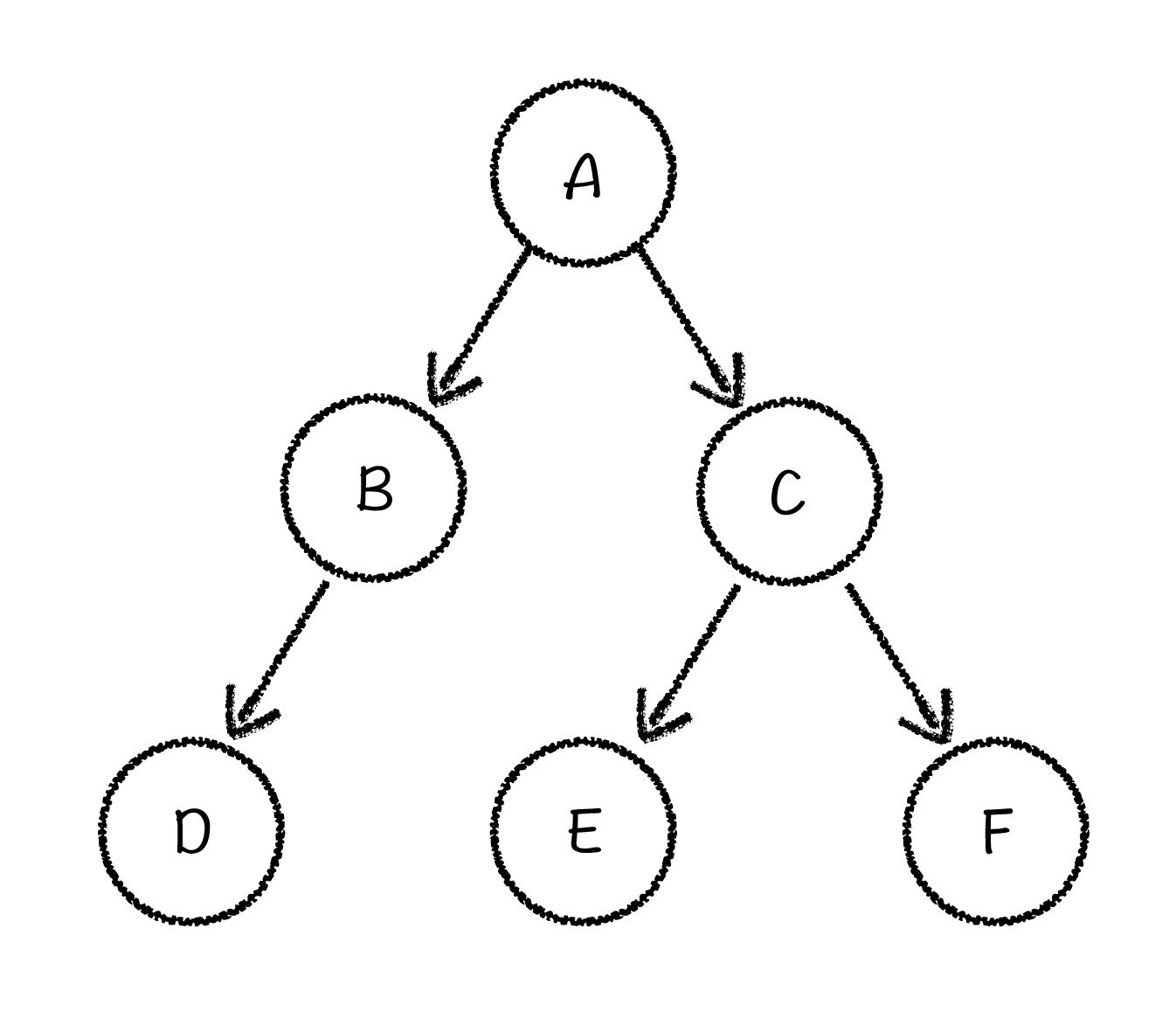
二叉树,就是每个节点下面最多有两个子节点的结构。如下图所示,就是一个二叉树结构:

我们把其中的 A 节点叫做“根节点”,B 和 C 是 A 节点的两个“子节点”,同理,E 和 F 是 C 节点的两个子节点,D 是 B 节点的子节点。如果更细致地划分,以 B 为根节点的子树,处于 A 节点的左侧,所以称为 A 节点的左子树,C 称为 A 节点的右子树。反过来,我们把 A 节点称为 B 和 C 节点的父节点,同时它也是 D、E、F 节点的祖先节点。以上就是二叉树中的一些基本概念了。
认识了二叉树的基本概念以后,我们接下来就来看看二叉树的三种遍历方式:前序遍历、中序遍历与后序遍历。

从图中可见,每一种遍历的方式,都是采用递归的定义方式。而所谓的前、中、后序遍历,其实说的是根节点的位置:根节点在左右子树遍历之前,那就是前序遍历;夹在左右子树中间,就是中序遍历;位于左右子树遍历之后,那就是后序遍历。
如果我们将图 1 中的二叉树结构,分别按照三种方式进行遍历,会得到如下所示的遍历结果:
前序遍历:A B D C E F
中序遍历:D B A E C F
后序遍历:D B E F C A
这里你一定要注意,在写某一种遍历结果的时候,一定是按照递归展开的方式。例如,在中序遍历中,我们是将根节点左子树所形成的中序遍历结果(D B),放在根节点 A 的左侧,然后是根节点 A,接着是根节点右子树的中序遍历结果(E C F)。所以最后,整棵树的中序遍历结果就是 D B A E C F。
介绍完了二叉树的基本概念及三种遍历方式后,我们接下来就要赋予这个二叉树结构一些实际的意义,让它能够帮助我们理解表达式求值的过程。
其实,任何一个四则混合运算的表达式,都能转换成相对应的二叉树,而原表达式的值,等于对应二叉树的后序遍历结果。例如,下图就是一个加法表达式和它所对应的表达式树:
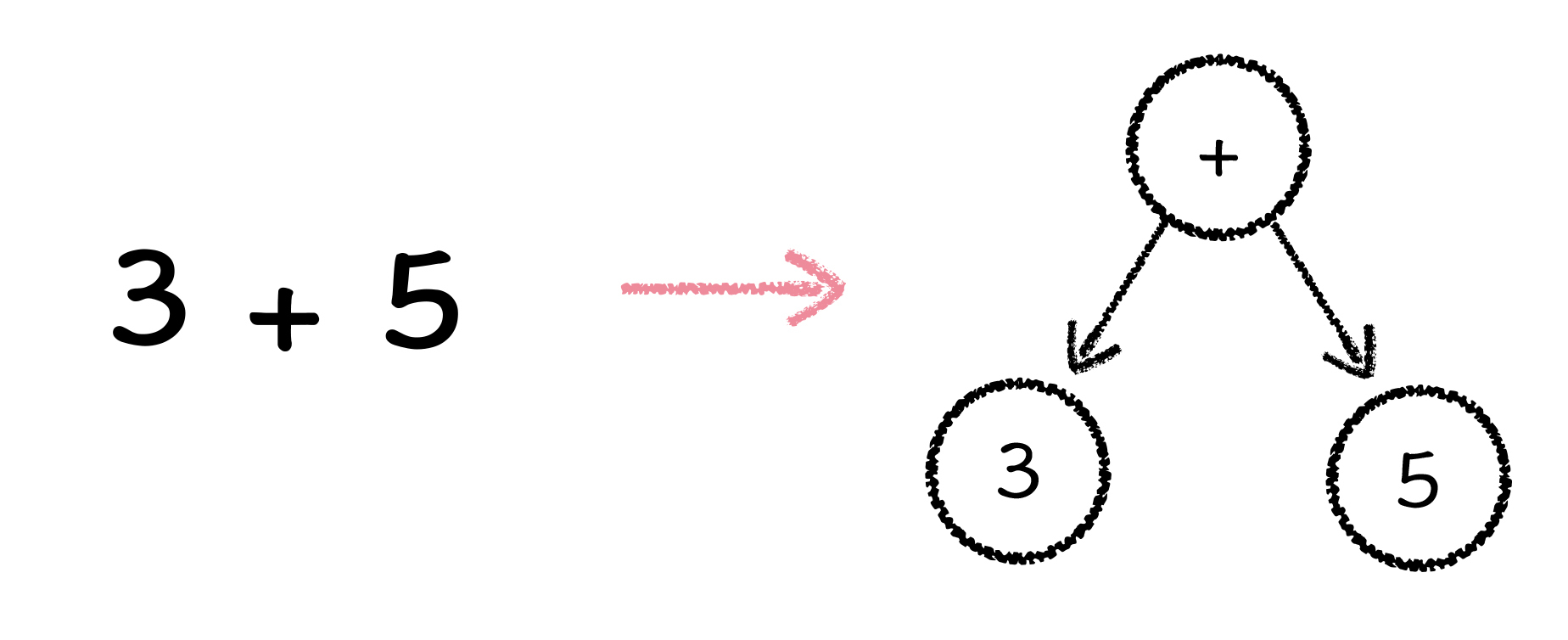
我们看到,在表达式树中,根节点就是运算符+(加号),加号的左子树是数字3,右子树是数字 5。根据刚刚所说的对应规则,在表达式树上,按照后序遍历的顺序,得到的就是表达式的值。图3中的表达式树,首先遍历得到左子树的数字3,再遍历得到右子树的数字 5,最后遍历到根节点的运算符+(加号),就将左右子树的值做加法,得到原表达式的结果 8。
下面,我们来看一个稍微复杂一点儿的表达式,以及它所对应的表达式树。
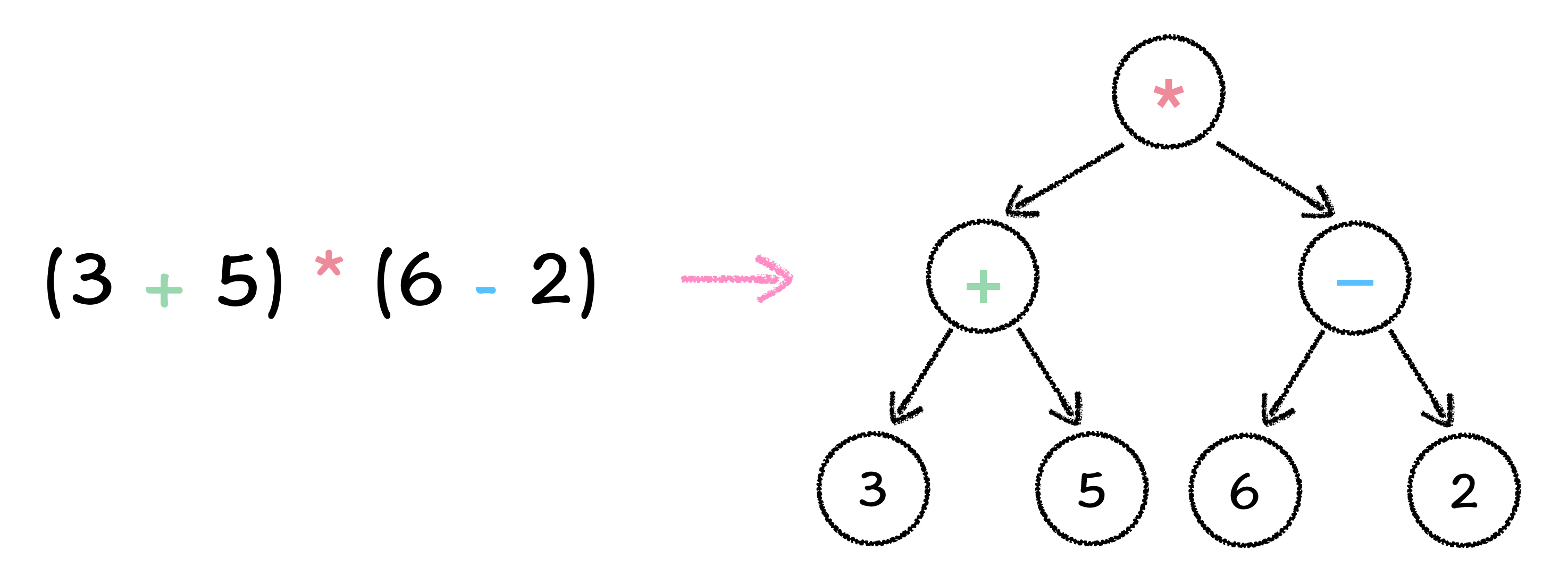
从图中可见,原表达式是(3 + 5) * (6 - 2),而其对应的表达式树中,已经没有了括号的影子。那括号的影响在表达式树上怎么体现呢?其实括号对表达式的影响,已经被表达式树转换成了等价的树形结构关系。这一点怎么理解呢,听我慢慢给你解释。
这里有个关键词,就是“顺序”。我们知道,表达式是按照计算顺序,得到计算结果的。表达式树,按照的是后序遍历方式,这本身也是规定了一种计算“顺序”。根据后序遍历规则,我们可以知道,表达式树的根节点所代表的运算,是原表达式中最后一个执行的运算。
我们回到示意图中具体示例来分析,图中表达式树的计算顺序应该是这样的:首先计算左子树所代表的 3 + 5 表达式的值,再计算右子树代表的 6 - 2表达式的值,最后根据根节点的乘法运算,计算得到左右子树的乘积值。
如此你会发现,表达式树的这种计算顺序,与原表达式添加了括号以后的计算顺序等价。
综上所述,我们可知,表达式树中越靠近根节点的运算符,优先级越低,而根节点代表了原表达式中,优先级最低的那个运算符。表达式中原有的括号,其实就是用来控制运算符之间的计算顺序的,这种计算顺序,对应的就是表达式树中的父子节点关系,这就是我们刚刚所说的,原表达式中的括号,被转换成了等价的树形结构关系的含义。
理解了表达式树以后,对于我们计算表达式的值,究竟有何作用呢?难道是在程序中,将读入的表达式字符串,转换成程序内的一棵表达式树结构么?
不知道你还记不记得,之前我们在讲链表结构的时候,提到链表不仅仅是一种程序中的结构,更重要的是它所体现出来的“链表思维”。其实今天我们学习的表达式树结构同样如此,我们不需要在程序中真正地建立一棵表达式树,而是利用表达式树去理解表达式计算的过程。
下面我们就来具体看看,如何利用这种思维,解决表达式计算问题。
我们知道,任何一个表达式,都对应一个等价的表达式树。而这个表达式树的根节点所对应的,就是原表达式中最后一个被计算的运算符。如果我们可以找到这个运算符在原表达式中的位置,那么这个运算符所的左边部分,对应的就是表达式树根节点的左子树,运算符的右边部分,对应的就是表达式树根节点的右子树。
我们用 String 代表原表达式字符串,op 代表整个表达式中最后一个被计算的运算符,L_String 是 op 运算符左边的字符串,R_String 就是右边的字符串。
假设,我们有一个函数 get_val(String),可以得到 String 所代表的表达式的值。那么关于 get_val(String),我们就可以得到如下递推关系:
get_val(String) = get_val(L_String) op get_val(R_String)
也就是当前表达式的值,等于左边表达式的值与右边表达式的值之间的运算结果。
这里我给你举个具体的例子,还是拿前面的那个乘法表达式来看:
get_val("(3+5)*(6-2)") = get_val("(3+5)") * get_val("(6-2)")
如果我们能确定,表达式字符串中最后一个被计算的运算符的位置,我们就可以把原表达式字符串分成两部分,进行递归求解。所以,找到最后一个被计算的运算符的位置,才是我们完成程序的关键。
到了这里,关于如何利用表达式树来解决表达式计算问题,我们就解释完了。
最后,我们就来看一下,确定运算符计算顺序的处理技巧。
怎么确定表达式中每一个运算符的计算顺序呢?其实我们可以通过给每个运算符赋予一个权重,权重越高,代表计算优先级越高。下面我就来说说这个权重是怎么设置。
根据四则混合运算的基础规则,我们可以给 +、-、*、/ 运算符设定一个基础权重,例如,+、- 权重是1,*、/ 权重是 2。
那括号呢?我们可以对括号里面的所有运算符,额外加上一个很大的权重。假设,运算符外有1 层括号,就额外增加权重 100。如果一个运算符被套在了两层括号里面,那它的权重就应该被额外加上 200。
按照这个规则,请你计算下面这个表达式中,每个运算符的权重:
((3 + 5) * 6) - 7 * 9 + 4
很简单,从左到右,运算符号依次是+、*、-、*、+,它们的运算符权重分别是 201、102、1、2、1。根据权重可知,最后一个被计算的运算符,应该是末尾权重为 1 的运算符,也就对应了表达式中最后一个+(加号)。根据这个加号所在位置,我们可以把表达式分成左右两部分,进行递归求解。
在实际编码过程中,我们可以记录一个值 temp,代表由括号产生的额外权重,当碰到左括号的时候,我们就给 temp 加上100,碰到右括号的时候,temp 就相应的减去 100。对于计算正常的 +、-、*、/ 运算符权重的时候,其权重值应该等于基础权重加上 temp 这个额外权重。
好了,整个程序的核心思路,我已经提供给你了,希望你能通过自己的思考,试着做出来。当然,如果你实在想不出来,可以参考文末我给出的参考代码。
至于如何定义变量,你可以先实现一个没有变量的表达式求值的程序,然后再将定义变量,作为一个新功能,加入到你的程序中。还记得我们之前讲的系统功能迭代过程吧?我们说:功能迭代,数据先行。对于定义变量这个功能的迭代,我们的实现过程也不例外,先思考清楚变量的值“如何存储,如何使用”,把这两个问题想明白了,功能也就开发完一半儿了。
最后,我们做一下课程小结。通过今天的课程,我希望你知道:
好了,今天的课程就到这里结束了。真的想跟你再说一次“我们下期见“,可送君千里,终有一别。初航我带你,远航靠自己,我是海贼胡船长,我们江湖再见。
参考代码
/*************************************************************************
> File Name: calc.cpp
> Author: hug
> Created Time: 五 3/27 22:13:04 2020
************************************************************************/
#include <stdio.h>
#include <string.h>
#define INF 0x3f3f3f3f
/*
* 计算表达式 str 从 l 到 r 位置的值
* */
int calc(const char *str, int l, int r) {
/*
* pos : 根节点运算符的位置,初始化为 -1
* priority : 根节点运算符的权重
* temp : 由括号产生的额外权重
* */
int pos = -1, priority = INF - 1, temp = 0;
for (int i = l; i <= r; i++) {
int cur_priority = INF;
switch (str[i]) {
case '(': temp += 100; break;
case ')': temp -= 100; break;
case '+':
case '-': cur_priority = 1 + temp;
case '*':
case '/': cur_priority = 2 + temp;
default: break;
}
/*
* cur_priority : 当前运算符的优先级
* 更新区间内最低优先级的运算符的位置
* */
if (cur_priority <= priority) {
pos = i;
priority = cur_priority;
}
}
/*
* 如果 pos == -1,说明这一段表达式中没有运算符
* 说明,这一段表达式中只有数字,也就是递归到了树的叶子结点
* */
if (pos == -1) {
int num = 0;
for (int i = l; i <= r; i++) {
if (str[i] < '0' || str[i] >= '9') continue;
num = num * 10 + (str[i] - '0');
}
return num;
}
/*
* 递归计算得到运算符左边及右边表达式的值
* 再根据当前运算符,得到当前表达式的值
* */
int a = calc(str, l, pos - 1);
int b = calc(str, pos + 1, r);
switch (str[pos]) {
case '+': return a + b;
case '-': return a - b;
case '*': return a * b;
case '/': return a / b;
}
return 0;
}
int get_val(const char *str) {
return calc(str, 0, strlen(str) - 1);
}
int main() {
char str[1000];
while (scanf("%[^\n]", str) != EOF) {
getchar();
printf("%s = %d\n", str, get_val(str));
}
return 0;
}