你好,我是卢誉声。
作为“初识动态规划”模块的第一节课,我会带着你一起从贪心算法开始了解整个知识体系的脉络。现实中,我们往往不愿意承认自己贪婪。事实上,贪婪是渴望而不知满足,它是人的一种基本驱动力。既然是基本驱动力,那它自然就不会太难。
所以你可能会说贪心算法很简单啊,但其实不然,这里面还真有不少门道值得我们说说。而且,它还跟动态规划问题有着千丝万缕的联系,能够帮助我们理解真正的动归问题。
接下来我们就从一个简单的算法问题开始探讨,那就是硬币找零。在开始前,我先提出一个问题:任何算法都有它的局限性,贪心算法也如此,那么贪心算法能解决哪些问题呢?
你不妨带着这个问题来学习下面的内容。
移动支付已经成为了我们日常生活当中的主流支付方式,无论是在便利店购买一瓶水,还是在超市或菜市场购买瓜果蔬菜等生活用品,无处不在的二维码让我们的支付操作变得异常便捷。
但在移动支付成为主流支付方式之前,我们常常需要面对一个简单问题,就是找零的问题。
虽然说硬币找零在日常生活中越来越少,但它仍然活跃在编程领域和面试问题当中,主要还是因为它极具代表性,也能多方面考察一个开发人员或面试者解决问题的能力。
既然如此,我们就先来看看这个算法问题的具体描述。
问题:给定n种不同面值的硬币,分别记为c[0], c[1], c[2], … c[n],同时还有一个总金额k,编写一个函数计算出最少需要几枚硬币凑出这个金额k?每种硬币的个数不限,且如果没有任何一种硬币组合能组成总金额时,返回 -1。
示例 1:
输入:c[0]=1, c[1]=2, c[2]=5, k=12
输出:3
解释:12 = 5 + 5 + 2
示例 2:
输入:c[0]=5, k=7
输出:-1
解释:只有一种面值为5的硬币,怎么都无法凑出总价值为7的零钱。
题目中有一个醒目的提示词,那就是“最少”。嗯,看起来这是一个求最值的问题,其实也好理解,如果题目不在这里设定这一条件,那么所求结果就不唯一了。
举个简单的例子,按照示例1的题设,有三种不同面值的硬币,分别为c1=1, c2=2, c3=5,在没有“最少”这一前提条件下你能罗列出几种不同的答案?我在这里随意列出几个:
解1:输出:5,因为 5 + 2 + 2 + 2 + 1 = 12。
解2:输出:6,因为 2 + 2 + 2 + 2 + 2 + 2 = 12。
解3:输出:12,因为 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 12。
所以,这是一个求最值的问题。那么求最值的核心问题是什么呢?嗯,无非就是穷举,显然,就是把所有可能的凑硬币方法都穷举出来,然后找找看最少需要多少枚硬币,那么最少的凑法,就是这道题目的答案。
在面试中,一般来说穷举从来都不是一个好方法。除非你要的结果就是所有的不同组合,而不是一个最值。但即便是求所有的不同组合,在计算的过程中也仍然会出现重复计算的问题,我们将这种现象称之为重叠子问题。
请你记住这个关键概念,它是动态规划当中的一个重要概念。但现在你只需要知道所谓重叠子问题就是:我们在罗列所有可能答案的过程中,可能存在重复计算的情况。我会在后续课程中与你深入探讨这个概念。
在尝试解决硬币找零问题前,我们先用较为严谨的定义来回顾一下贪心算法的概念。
所谓贪心算法,就是指它的每一步计算作出的都是在当前看起来最好的选择,也就是说它所作出的选择只是在某种意义上的局部最优选择,并不从整体最优考虑。在这里,我把这两种选择的思路称作局部最优解和整体最优解。
因此,我们可以得到贪心算法的基本思路:
现在让我们回到这个问题上来。
既然这道题问的是最少需要几枚硬币凑出金额k,那么是否可以尝试使用贪心的思想来解这个问题呢?从面值最大的硬币开始兑换,最后得出的硬币总数很有可能就是最少的。
这个想法不错,让我们一起来试一试。
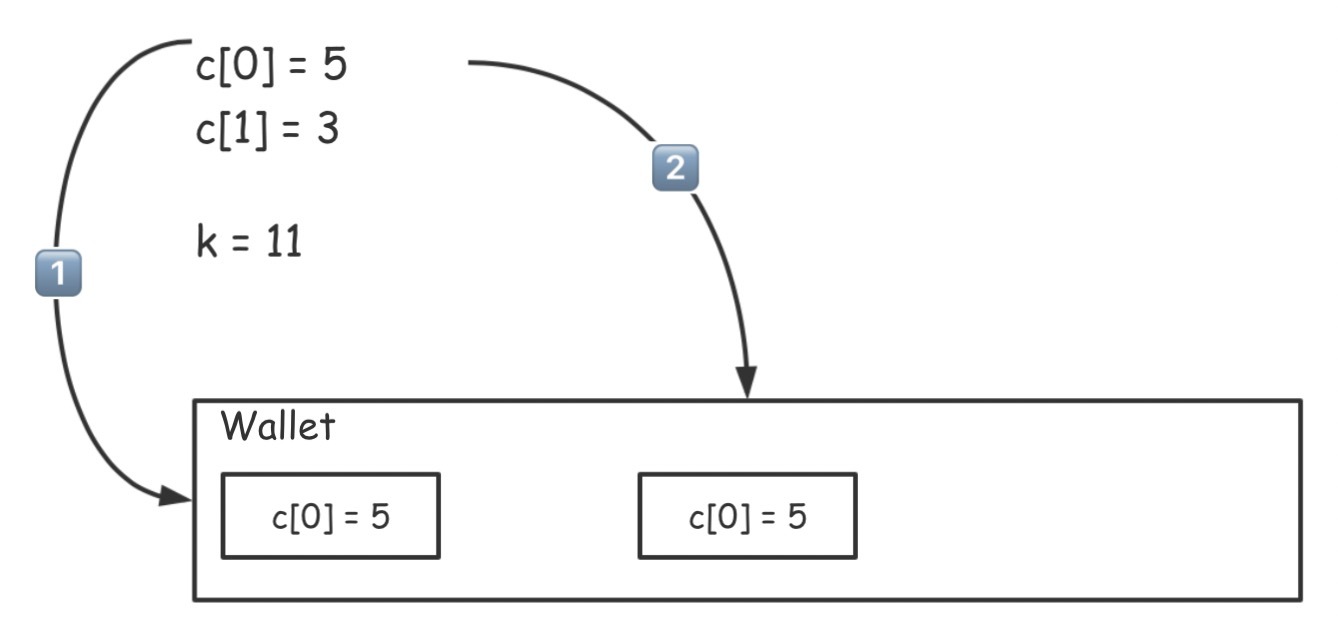
我用一个例子,带你看下整个贪心算法求解的过程,我们从 c[0]=5, c[1]=3 且k=11 的情况下寻求最少硬币数。按照“贪心原则”,我们先挑选面值最大的,即为5的硬币放入钱包。接着,还有6元待解(即11-5 = 6)。这时,我们再次“贪心”,放入5元面值的硬币。

这样来看,贪心算法其实不难吧。我在这里把代码贴出来,你可以结合代码再理解一下算法的执行步骤。
Java 实现:
int getMinCoinCountHelper(int total, int[] values, int valueCount) {
int rest = total;
int count = 0;
// 从大到小遍历所有面值
for (int i = 0; i < valueCount; ++ i) {
int currentCount = rest / values[i]; // 计算当前面值最多能用多少个
rest -= currentCount * values[i]; // 计算使用完当前面值后的余额
count += currentCount; // 增加当前面额用量
if (rest == 0) {
return count;
}
}
return -1; // 如果到这里说明无法凑出总价,返回-1
}
int getMinCoinCount() {
int[] values = { 5, 3 }; // 硬币面值
int total = 11; // 总价
return getMinCoinCountHelper(total, values, 2); // 输出结果
}
C++ 实现:
int GetMinCoinCountHelper(int total, int* values, int valueCount) {
int rest = total;
int count = 0;
// 从大到小遍历所有面值
for (int i = 0; i < valueCount; ++ i) {
int currentCount = rest / values[i]; // 计算当前面值最多能用多少个
rest -= currentCount * values[i]; // 计算使用完当前面值后的余额
count += currentCount; // 增加当前面额用量
if (rest == 0) {
return count;
}
}
return -1; // 如果到这里说明无法凑出总价,返回-1
}
int GetMinCoinCount() {
int values[] = { 5, 3 }; // 硬币面值
int total = 11; // 总价
return GetMinCoinCountHelper(total, values, 2); // 输出结果
}
这段代码就是简单地从最大的面值开始尝试,每次都会把当前面值的硬币尽量用光,然后才会尝试下一种面值的货币。
嗯。。。你有没有发现问题?那就是还剩1元零钱待找,但是我们只有c[0]=5, c[1]=3两种面值的硬币,怎么办?这个问题无解了,该返回-1了吗?显然不是。
我们把第2步放入的5元硬币取出,放入面值为3元的硬币试试看。这时,你就会发现,我们还剩3元零钱待找。
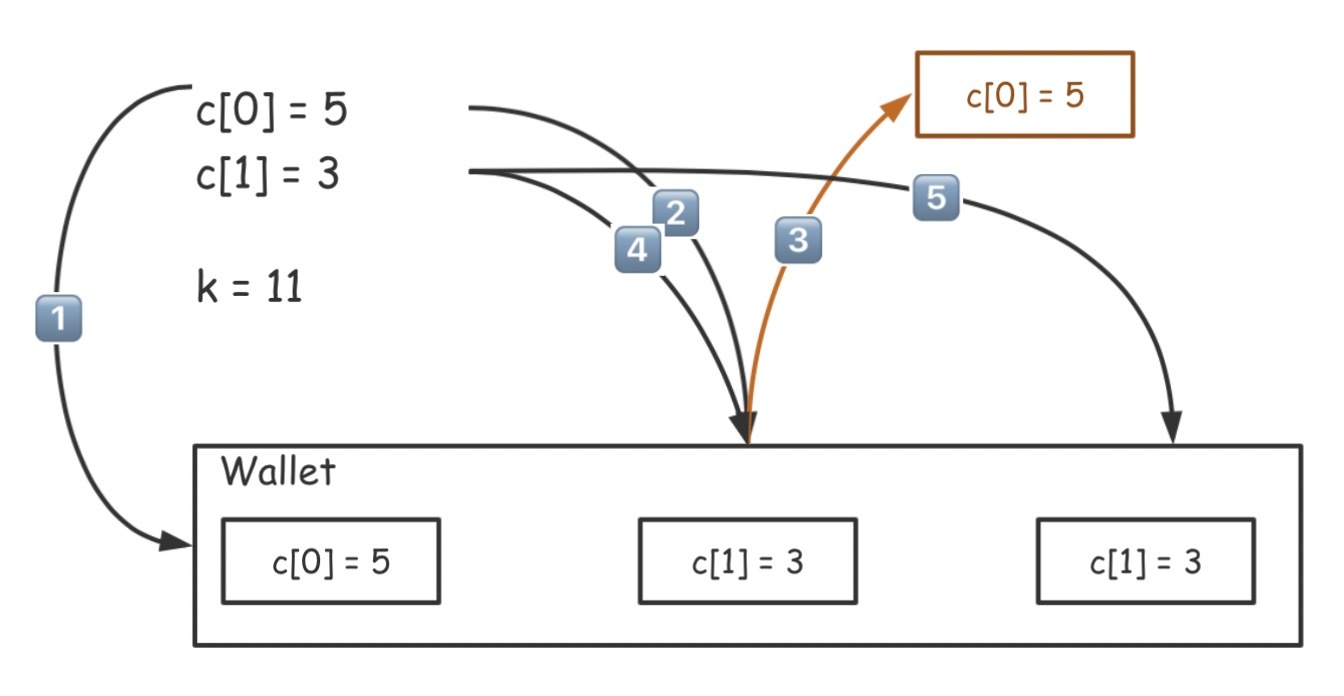
正好我们还有c[1]=3的硬币可以使用,因此解是c[0]=5, c[1]=3, c[1]=3,即最少使用三枚硬币凑出了k=11这个金额。
我们对贪心算法做了改进,引入了回溯来解决前面碰到的“过于贪心”的问题。同样地,我把改进后的代码贴在这,你可以再看看跟之前算法实现的区别。
Java 实现:
int getMinCoinCountOfValue(int total, int[] values, int valueIndex) {
int valueCount = values.length;
if (valueIndex == valueCount) { return Integer.MAX_VALUE; }
int minResult = Integer.MAX_VALUE;
int currentValue = values[valueIndex];
int maxCount = total / currentValue;
for (int count = maxCount; count >= 0; count --) {
int rest = total - count * currentValue;
// 如果rest为0,表示余额已除尽,组合完成
if (rest == 0) {
minResult = Math.min(minResult, count);
break;
}
// 否则尝试用剩余面值求当前余额的硬币总数
int restCount = getMinCoinCountOfValue(rest, values, valueIndex + 1);
// 如果后续没有可用组合
if (restCount == Integer.MAX_VALUE) {
// 如果当前面值已经为0,返回-1表示尝试失败
if (count == 0) { break; }
// 否则尝试把当前面值-1
continue;
}
minResult = Math.min(minResult, count + restCount);
}
return minResult;
}
int getMinCoinCountLoop(int total, int[] values, int k) {
int minCount = Integer.MAX_VALUE;
int valueCount = values.length;
if (k == valueCount) {
return Math.min(minCount, getMinCoinCountOfValue(total, values, 0));
}
for (int i = k; i <= valueCount - 1; i++) {
// k位置已经排列好
int t = values[k];
values[k] = values[i];
values[i]=t;
minCount = Math.min(minCount, getMinCoinCountLoop(total, values, k + 1)); // 考虑后一位
// 回溯
t = values[k];
values[k] = values[i];
values[i]=t;
}
return minCount;
}
int getMinCoinCountOfValue() {
int[] values = { 5, 3 }; // 硬币面值
int total = 11; // 总价
int minCoin = getMinCoinCountLoop(total, values, 0);
return (minCoin == Integer.MAX_VALUE) ? -1 : minCoin; // 输出答案
}
C++ 实现:
int GetMinCoinCountOfValue(int total, int* values, int valueIndex, int valueCount) {
if (valueIndex == valueCount) { return INT_MAX; }
int minResult = INT_MAX;
int currentValue = values[valueIndex];
int maxCount = total / currentValue;
for (int count = maxCount; count >= 0; count --) {
int rest = total - count * currentValue;
// 如果rest为0,表示余额已除尽,组合完成
if (rest == 0) {
minResult = min(minResult, count);
break;
}
// 否则尝试用剩余面值求当前余额的硬币总数
int restCount = GetMinCoinCountOfValue(rest, values, valueIndex + 1, valueCount);
// 如果后续没有可用组合
if (restCount == INT_MAX) {
// 如果当前面值已经为0,返回-1表示尝试失败
if (count == 0) { break; }
// 否则尝试把当前面值-1
continue;
}
minResult = min(minResult, count + restCount);
}
return minResult;
}
int GetMinCoinCountLoop(int total, int* values, int valueCount, int k) {
int minCount = INT_MAX;
if (k == valueCount) {
return min(minCount, GetMinCoinCountOfValue(total, values, 0, valueCount));
}
for (int i = k; i <= valueCount - 1; i++) {
// k位置已经排列好
int t = values[k];
values[k] = values[i];
values[i]=t;
minCount = min(minCount, GetMinCoinCountOfValue(total, values, 0, valueCount));
minCount = min(minCount, GetMinCoinCountLoop(total, values, valueCount, k + 1)); // 考虑后一位
// 回溯
t = values[k];
values[k] = values[i];
values[i]=t;
}
return minCount;
}
int GetMinCoinCountOfValue() {
int values[] = { 5, 3 }; // 硬币面值
int total = 11; // 总价
int minCoin = GetMinCoinCountLoop(total, values, 2, 0);
return (minCoin == INT_MAX) ? -1 : minCoin;
}
改进后的算法实现在之前的基础上增加上了一个回溯过程。简单地说就是多了一个递归,不断尝试用更少的当前面值来拼凑。只要有一个组合成功,我们就返回总数,如果所有组合都尝试失败,就返回-1。
嗯,这样就没问题了,对硬币找零问题来说,我们得到了理想的结果。
从上面这个例子我们可以看出,如果只是简单采用贪心的思路,那么到用完2个5元硬币的时候我们就已经黔驴技穷了——因为剩下的1元无论如何都没法用现在的硬币凑出来。这是什么问题导致的呢?
这就是贪心算法所谓的局部最优导致的问题,因为我们每一步都尽量多地使用面值最大的硬币,因为这样数量肯定最小,但是有的时候我们就进入了死胡同,就好比上面这个例子。
所谓局部最优,就是只考虑“当前”的最大利益,既不向前多看一步,也不向后多看一步,导致每次都只用当前阶段的最优解。
那么如果纯粹采用这种策略我们就永远无法达到整体最优,也就无法求得题目的答案了。至于能得到答案的情况那就是我们走狗屎运了。
虽然纯粹的贪心算法作用有限,但是这种求解局部最优的思路在方向上肯定是对的,毕竟所谓的整体最优肯定是从很多个局部最优中选择出来的,因此所有最优化问题的基础都是贪心算法。
回到前面的例子,我只不过是在贪心的基础上加入了失败后的回溯,稍微牺牲一点当前利益,仅仅是希望通过下一个硬币面值的局部最优达到最终可行的整体最优。
所有贪心的思路就是我们最优化求解的根本思想,所有的方法只不过是针对贪心思路的改进和优化而已。回溯解决的是正确性问题,而动态规划则是解决时间复杂度的问题。
贪心算法是求解整体最优的真正思路源头,这就是为什么我们要在课程的一开始就从贪心算法讲起。
硬币找零问题本质上是求最值问题。事实上,动态规划问题的一般形式就是求最值,而求最值的核心思想是穷举。这是因为只要我们能够找到所有可能的答案,从中挑选出最优的解就是算法问题的结果。
在没有优化的情况下,穷举从来就不算是一个好方法。所以我带你使用了贪心算法来解题,它是一种使用局部最优思想解题的算法(即从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的速度去求得更好的解,当达到算法中的某一步不能再继续前进时,算法停止)。
但是通过硬币找零问题,我们也发现了贪心算法本身的局限性:
我们往往需要使用回溯来优化贪心算法,否则就会导致算法失效。因此,在求解最值问题时,我们需要更好的方法来解。在后面课程讲到递归和穷举优化问题的时候,我会讲到解决最值问题的正确思路和方法:考虑整体最优的问题。
在递归问题中,回溯是一种经典的优化算法性能的方法。递归对动态规划来说也十分重要。你能否举出使用回溯算法来解的面试问题?并给出你的解。希望你能在课后提出问题,进行练习。
最后,欢迎留言和我分享你的思考,我会第一时间给你反馈。如果今天的内容对你有所启发,也欢迎把它分享给你身边的朋友,邀请他一起学习!
评论