你好,我是范学雷。
上一讲,我们列举了常见的单向散列函数,我们还知道了退役的、遗留的和现行的算法,通过对处理能力限制和算法的性能的讨论,我们对如何选择哈希算法有了更明确的认知。
还记得我们留了一个小尾巴吗?我们提到了“长度延展攻击”。“长度延展攻击”是怎么一回事?我们为什么要了解它?在单向散列函数的使用上,我们需要注意哪些安全问题?
这就是我们这一次要解决的事情。
我们先来看看什么是“长度延展”,这样会有利于你理解“长度延展攻击”。
现在,假设我们有两段数据,S和M,以及一个单向散列函数h。如果我们要把这两段数据合并起来,并且还要计算合并后的散列值,这就叫做单向散列函数的长度延展。
不过,问题来了,是S放在前面(h(S|M)),还是M放在前面(h(M|S))?既然,我们说,散列值是无法预测的,那么,数据编排的顺序有意义吗?
如果S和M都是公开的信息,顺序是不重要的。可如果S是机密信息,M是公开信息,这两段数据的排列顺序就至关重要了。如果机密信息放在了前面,就存在“长度延展攻击”的风险。
弄清楚了长度延展,长度延展攻击就很好理解了,就是说我们可以利用已知数据的散列值,计算原数据外加一段延展数据后的散列值。也就是说,如果我们知道了h(S|M),我们就可以计算h(S|M|N)。其中,数据N就是原数据追加的延展数据。
如果S和M都是公开的信息,能够计算延展数据的散列值也没什么紧要的。但是,如果S是机密数据,它的用途一般就和机密有点关系。比如说,因为没有人知道我拥有的机密数据S,所以,当我给定一段公开信息M后,只有我自己才能计算S和M的散列值。
通过验证S和M的散列值,我就知道一个给定散列值是我计算、派发出去的,还是别人伪造的。
比如下面的这段数据:
key_id=44fefa051fc1c61f5e76f27e620f51d5&perms=read&hash_sig=38d39516d896f879d403bd327a932d9e
其中,key_id表示机密数据的编号,perms表示操作权限,hash_sig是使用机密数据key对perms的签名。签名的计算,就是使用单向散列函数:
sig = h(key|perms)
由于使用了机密数据key,按照设想,这段数据只能由机密数据的持有者生成,然后分发出去,供授权的人使用。机密数据的持有者接收到这样的数据后,重新计算数据签名,然后对比请求数据里的签名。如果两个签名相同,就表示这是一个自己生成的、合法的授权,就可以授予请求数据所要求的权利。
不过,这个设计就存在“长度延展攻击”的风险。攻击者并不需要知道机密数据,就可以通过一个已知的URL,构造出一个新的合法的URL,从而获得不同的授权。
伪造的数据看起来像下面的样子:
key_id=44fefa051fc1c61f5e76f27e620f51d5&perms=read\0x80\0x00...\0x02&delete&hash_sig=a8e6b9704f1da6ae779ad481c4c165a3
在这段伪造的数据中,0x80到0x02之间的数据是数据块补齐数据,而且新添加了删除的权限,并且重新计算、替换了数据签名。
其中,数据签名需要使用机密数据,而攻击者并不知道机密数据,那么攻击者怎样伪造数据签名呢?要解决这个疑问,我们需要先看看单向散列函数的构造。
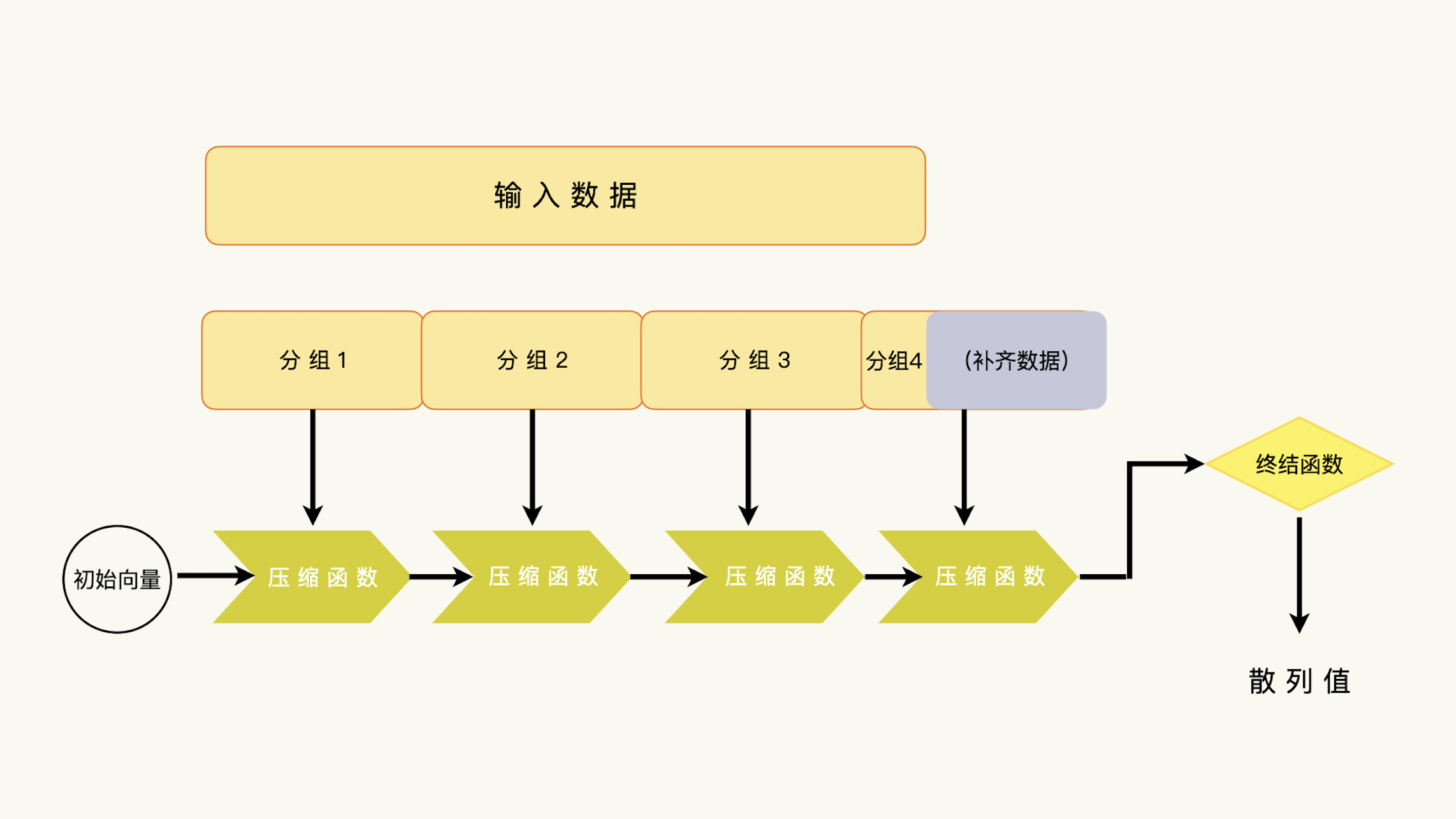
我们在上一讲简单地提到过,一起来重新回顾一下。一个典型的单向散列函数,应该由四个部分组成:数据分组、链接模式、压缩函数和终结函数。
我们之前着重说了数据分组,我们现在来看看其他的部分:

值得一提的是,在MD5,SHA-1,SHA-256和SHA-512的算法设计中,终结函数就是把压缩函数的输出向量排列成一个字节串。知道了字节串,我们也就知道了压缩函数的输出向量。
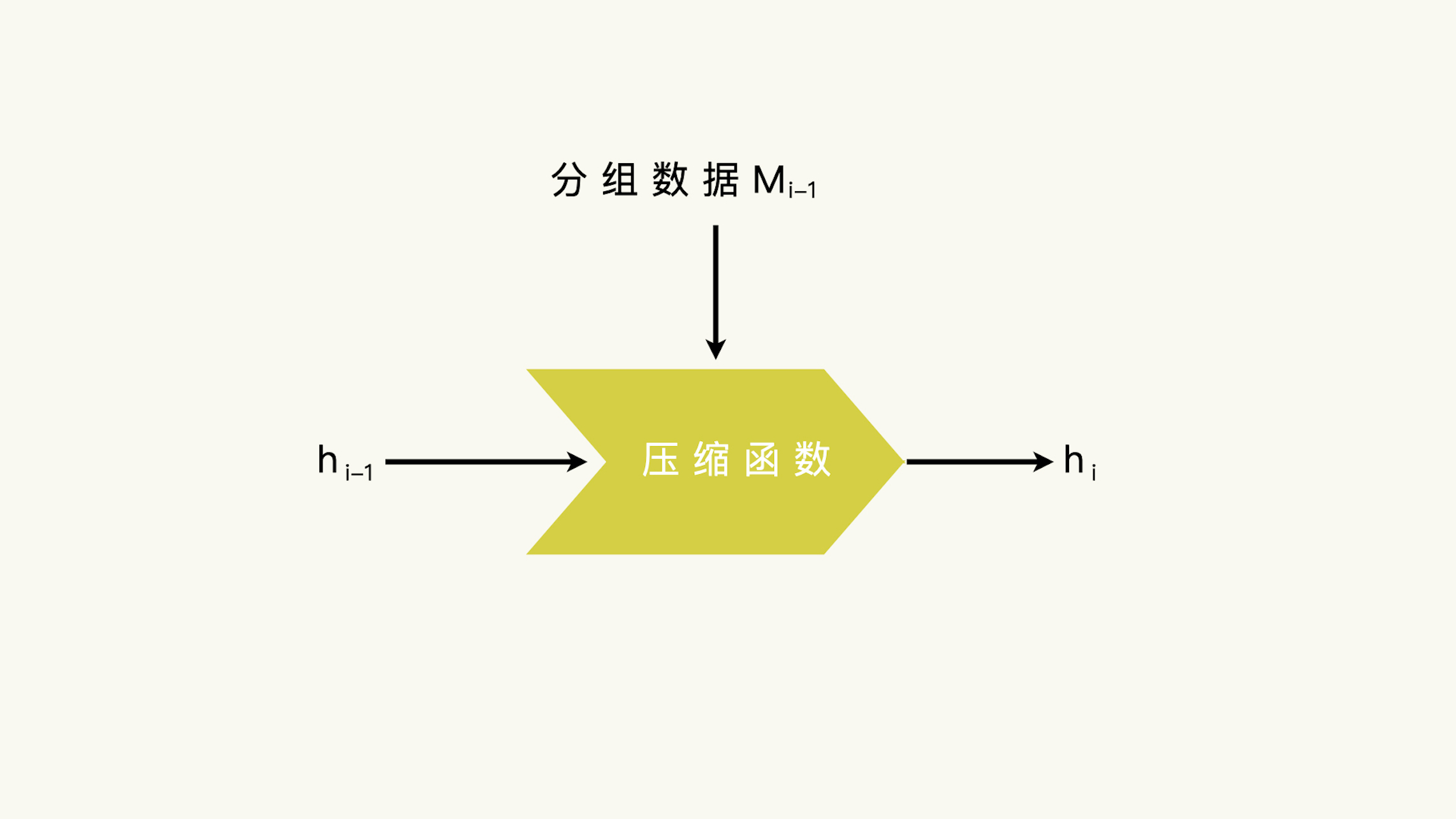
压缩函数接收一个数据分组和上一个压缩函数的运算结果。如果知道了上一个压缩函数的运算结果,我们就能够计算下一个分组数据的压缩函数运算结果。这里,就是出现安全漏洞的地方。
我们把原来的散列值作为压缩函数的一个输入,我们再按照数据补齐规范,去补齐原来数据到数据分组的整数倍,然后加入新的数据,我们就可以计算原数据和扩展数据的散列值了。
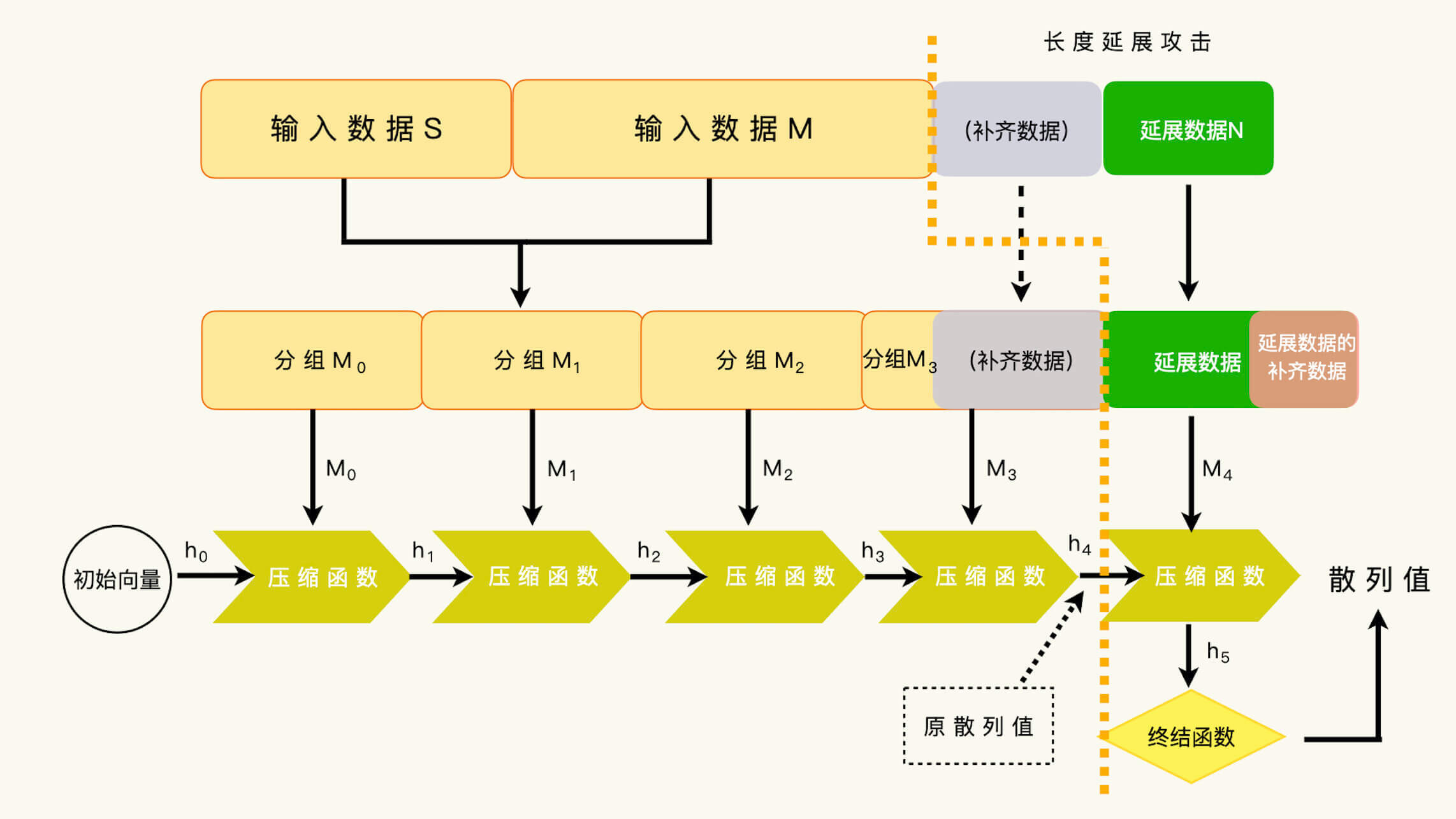
新的散列值的计算,不需要知道预先设想的机密数据。但是整个散列值的计算,又的确使用了机密数据。只不过,这个计算过程需要两个部分,第一部分由机密数据的持有者计算,第二部分是攻击者使用第一部分的结果,伪造了一个使用了机密数据的散列值。
但是,如果我们把数据编排顺序换一下,把公开信息M放在前面,机密信息S放在后面,长度延展攻击就不起作用了。这就是数据编排顺序对数据安全性的影响。
一个单向散列函数,只要使用了类似上述的压缩函数和链接模式,都是“长度延展攻击”的可疑对象。我们上一次提到的MD2、MD5、SHA-0、SHA-1、SHA-2,都有长度延展攻击的风险。其中,对于下列算法,长度延展攻击是完全有效的:
对于下列算法,长度延展攻击虽然不是完全有效,但是算法的安全级别显著降低了:
对于下列算法,长度延展攻击没有效果(包括所有的SHA-3算法):
上面这么长的列表,你是不是觉得好多,有点烦?其实,我们讨论长度延展攻击,目的不是让你记住上述的列表。
我们要从中学会、理解一个实用的经验:不要单纯使用单向散列函数来处理既包含机密信息、又包含公开信息的数据。即使我们把机密信息放在最后处理,这种使用方式也不省心。
如果我们需要使用机密数据产生数据的签名,我们应该使用设计好的、经过验证的算法,比如我们后面会讨论的消息验证码(Message Authentication Code)和基于单向散列函数的消息验证码(Hash-based Message Authentication Code)。
另外,如果需要设计算法,我们还要理解另外一个实用的原则:算法要皮实、耐用,不能有意无意地用错了就有安全漏洞。你看,SHA-1和SHA-2已经很简单、皮实了,用错了场景还是有严重的问题。相比之下,SHA-3同样简单,但是更皮实。
这和我们在《代码精进之路》的专栏里反复讨论的API要简单、直观、皮实,是一个道理。
既然我们不能单纯地使用单向散列函数处理混合了机密信息和公开信息的数据。那我们能不能单纯地使用机密信息,或者单纯地使用公开信息?回答这个问题,还要看具体的使用场景。
我们已经知道了,单向散列函数是密码学的核心。下面是一些典型的使用单向散列函数的场景:
还记得我们在之前,讨论过了怎么使用单向散列函数校验数据完整性。
输入:
1、数据D
2、原始数据的散列值H
3、计算散列值使用的散列函数
输出:
数据D是不是完整的?
运算:
1、使用散列函数计算数据D的散列值H';
2、对比数据的散列值H和计算获得的散列值,如果两个散列值相同,则数据D是完整的;否则,数据D是修改过的数据。
如果我们单纯地使用单向散列函数校验数据完整性,是要对比数据的散列值的。既然是对比,也就意味着有两个散列值。这时候,我们需要考虑的主要问题就是:给定的散列值有没有被更改?
散列值的计算是公开的,给定一段数据,谁都可以计算它的散列值。如果数据可以被修改,而且给定的散列值也是修改后的数据的散列值,这个数据完整性校验是没有意义的。
所以,单纯使用单向散列函数去校验数据的完整性,我们需要确保给定的散列值是不能被修改的,这就是这个使用场景的限制。
其余的单向散列函数的使用场景,我们后面还会接着讨论。
今天,我们讨论了单向散列函数的长度延展攻击,以及使用单向散列函数需要注意的事项,还列举了典型的单向散列函数使用场景。
通过今天的讨论,我们要:
另外,今天也是单向散列函数这一模块的最后一讲了。我们也来小结一下这一模块要注意的知识点,拉个清单。
在这一模块里,我们要掌握下面的基本概念和最佳实践:
好的,又到了留思考题的时间了。
今天的思考题是一个拓展题,你要自己去发现单向散列函数的更多适用场景。
我们一直强调,使用单向散列函数校验数据完整性,需要保证原始的散列值不能被更改。你能不能找到一些场景,可以让我们不用担心原始的散列值被更改,单纯使用单向散列函数就可以校验数据完整性?
除了我们上面列出来的一些场景,你能不能找出更多的单向散列函数使用场景?比如说,利用散列值长度固定的特点,利用碰撞困难的特点?
欢迎在留言区留言,记录、讨论你发现的新使用场景。
好的,今天就这样,我们下次再聊。