你好，我是范学雷。

上一讲，我们讨论了对称密钥分组算法的CBC链接模式，还提到了异或运算的好处，以及它的风险。但是，我们又留了一个小尾巴，异或运算是怎样带来麻烦的？它是怎么影响CBC链接模式的安全性的？我们又有什么有效的办法可以规避异或运算的风险？

这两次讨论，有点烧脑，我们姑且把它当做一次打怪升级的过程。如果弄清楚这些问题，你就可以更得心应手地使用分组算法，而且毫无疑问地超越了大部分人对对称密钥分组算法的理解。

鉴于这两次讨论的难度，我觉得最好的学习方式，就是拿上纸笔，跟着我的思路，自己画一画攻击的流程。学习一段内容，就画一画这一段的思路，扎扎实实把这一段理解下来。

其实，这也是我们学习、理解所有密码学算法攻击的一个办法。密码学算法的攻击，大部分都超乎想象，意想不到。读一段、画一段，理解一段，是一个实用的方法，也是我自己使用的方法。

好，你准备好了吗？我们开始了。

怎么利用解密端攻击？

还记得CBC模式吗？攻击者既可以攻击它的解密端，也可以攻击它的加密端。针对解密端的攻击，最常见的方式，就是给定密文数据，观测解密运算是成功还是失败。

那么，解密端是怎么知道解密是成功还是失败呢？到目前为止，在我们已经讨论过的密码学技术中，我们唯一能够利用的，就是数据补齐方案。我们先来看看，数据怎么补齐？

数据怎么补齐？

简单来说，CBC模式的补齐数据，就是一个数据分组缺失的数据的长度。比如，对于AES来说，数据分组是16个字节。如果一段数据只有15个字节，补齐的数据就是一个1；如果有14个字节，补齐的数据就是两个2；以此类推，如果只有一个字节，补齐的数据就是十五个15 。

不过，这个数据补齐方案有明显的缺陷。

当数据分组最后一个字节是1，解密端不太好判断这个字节到底是补齐数据，还是有效数据。所以，很多标准和协议使用最后一个数据分组的最后一个字节来标明补齐数据。

如果一段数据只有15个字节，补齐的数据就只有这个标识字节，数值为0，表示没有额外的补齐数据；如果有14个字节，标识字节为1，表示还有一个字节的额外补齐数据，额外的补齐数据的数值也是1；如果有13个字节，标识字节为2，表示还有两个字节额外补齐数据，额外的补齐数据的数值也是2；以此类推。

需要注意的是，如果一段数据有16个字节，也就是刚好一个数据分组大小，这时候，就需要一个全是补齐数据的数据分组，它的每一个字节都是15。

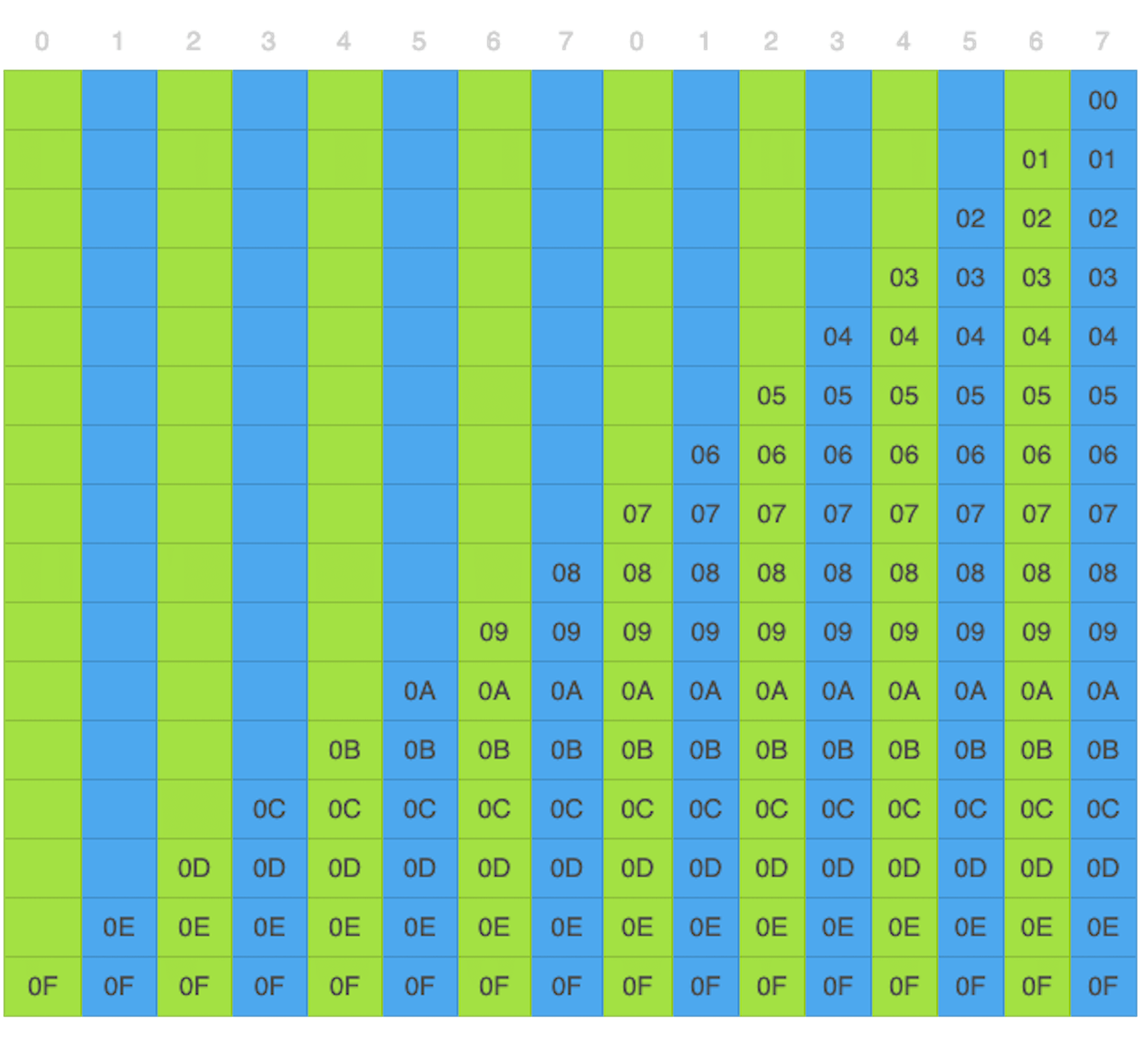
为了方便，下面的讨论中，我们都使用有标识字节的数据补齐方案，除非特别声明。

补齐怎么校验？

那你会不会有疑问，我们如何在解密端，判断一个数据分组中的数据是不是补齐数据？

可以检查最后的几位数字是不是相同。比如说，如果最后一位是2，但是倒数第二位和倒数第三位不是2，解密就失败了。失败的原因，可能是由于篡改的密文分组，或者是篡改的初始化向量，或者是篡改的密钥。不管哪种原因，都可能导致补齐数据的校验失败。

那我们怎么利用数据补齐方案展开攻击呢？

攻击怎么展开？

我们回顾一下CBC模式的解密过程。一个密文分组的解密，需要如下的输入数据：

• 上一次的密文分组Ci-1；
• 这一次的密文分组Ci；
• 加密和解密共享的密钥K。

这一次的密文分组Ci和密钥K，通过解密函数的运算，可以产生一个中间结果Ti，也就是解密函数运算的中间结果Ti；然后，解密函数运算结果Ti和上一次的密文分组进行异或运算，获得明文分组Pi，Pi = Ci-1 ^ Ti。

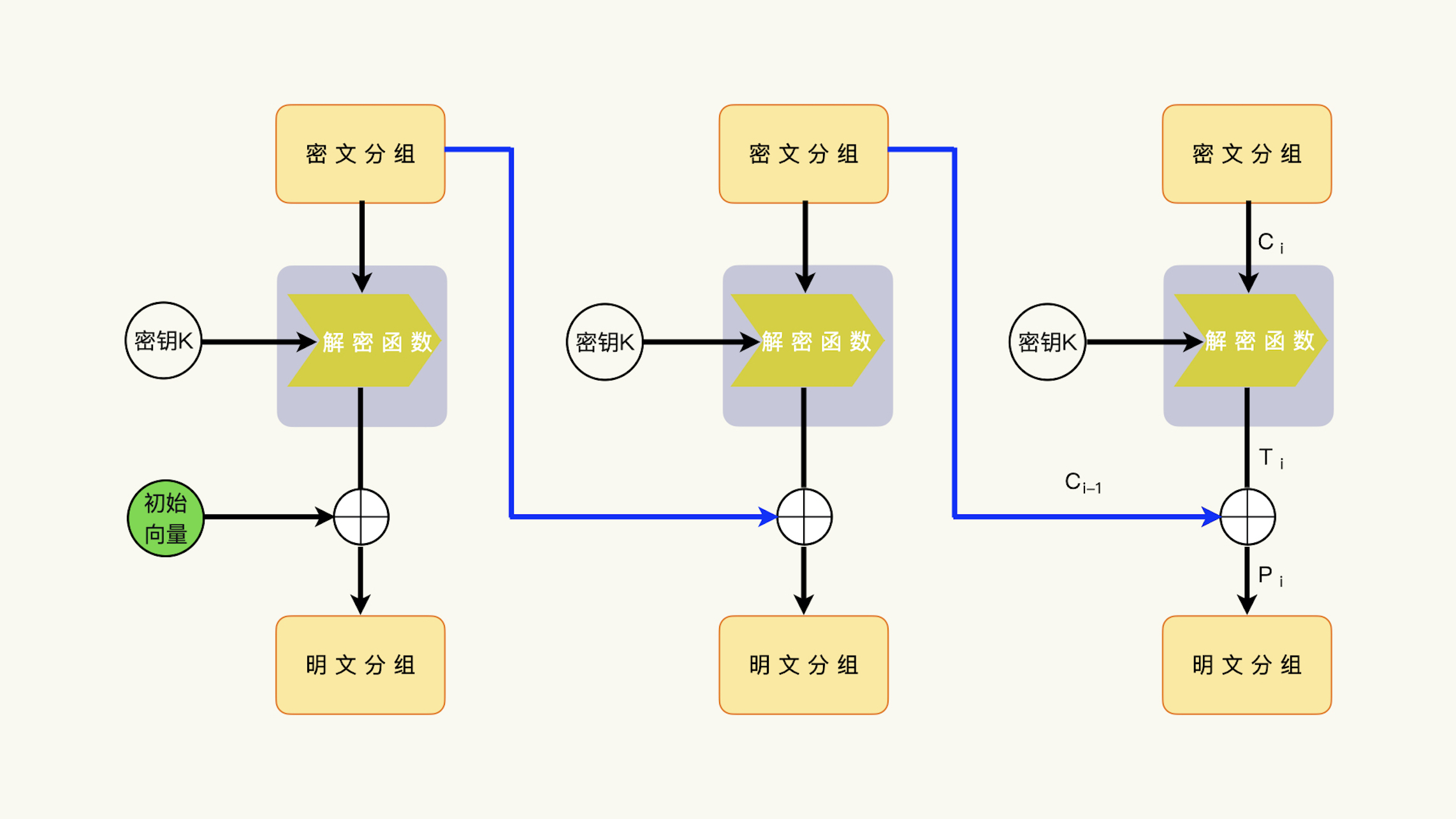
接下来，我们利用数据补齐方案的攻击，通过修改、构造最后一个密文分组Cn的前一个密文分组Cn-1，也就是倒数第二个密文分组，然后让解密端解密构造后的密文数据，观察修改了密文数据的解密能不能成功。

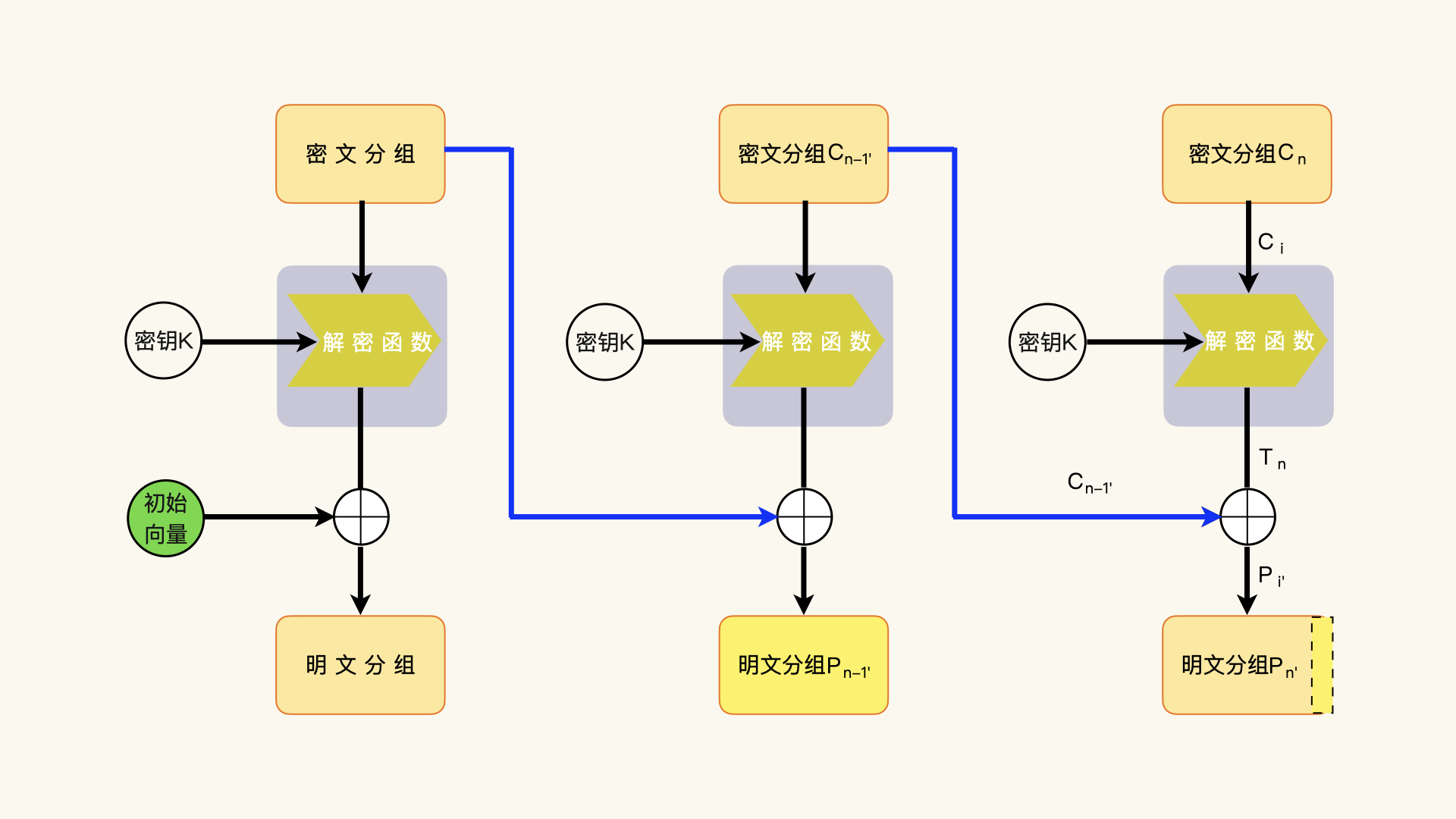
那倒数第二个密文分组该怎么构造呢？首先，修改该密文分组的最后一个字节，该字节可以从零开始。毫无疑问，解密端并不能正确解密该密文分组，得到的明文分组也不是期望的明文数据。

但是，正像我们前面讨论的，解密端并没有办法知道这一个密文分组解密失败。要判断解密是否成功，还需要判断最后一个明文分组的补齐数据是不是符合规范。

如果我们修改倒数第二个密文分组的最后一个字节，那么解密后的最后一个明文分组应该只有最后一个字节受到影响。如果这个解密后的字节是零，其他的数据会被解读为有效数据，这样就会通过补齐数据的校验。如果这个解密后的字节是其他数值，补齐数据的校验通过的概率就很小。实际的攻击过程，这么一点小小的概率也可以优化过滤掉。

如果解密后的这个字节不是零，那么，补齐数据的校验就会失败，解密端就会报错。观察解密端的行为，攻击者就能了解到，这个构造的字节没有通过解密过程。如果观察到失败，攻击者就会调节最后一个字节的数值，比如数值加一，然后再次让解密端尝试解密。

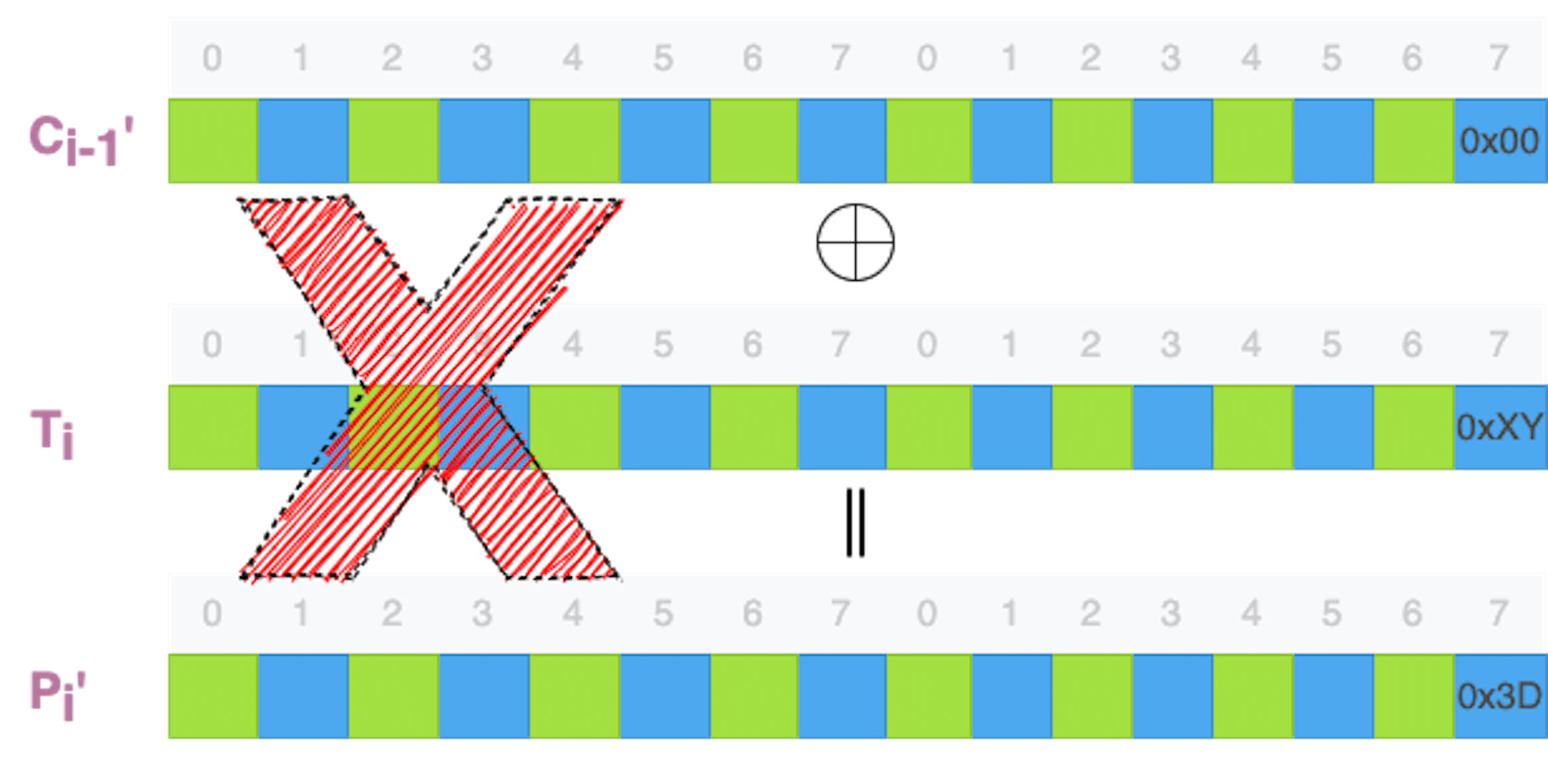
一个字节只有256种可能性，最多尝试255次，一定会有一次尝试，补齐数据是零。

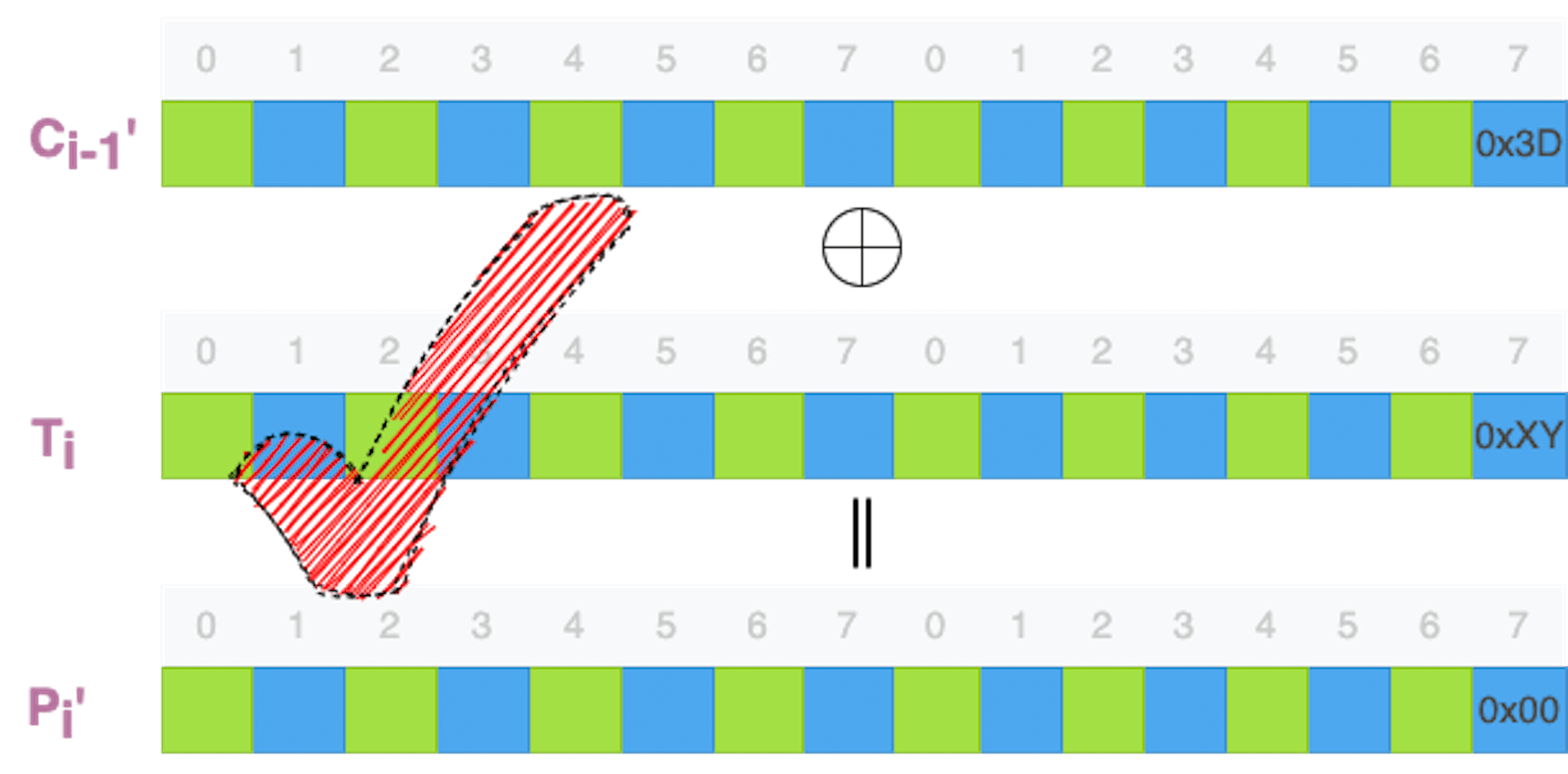
当攻击者观察到解密成功时，他能够掌握哪些数据呢？他能够直接得到的数据包括：

• 未修改密文分组的最后一个字节的数值（Cn-1[15]）；
• 修改后密文分组的最后一个字节的数值（Cn-1'[15]）；
• 解密端明文分组的最后一个字节的数值（Pn'[15]，也就是0x00）。

通过计算，他还可以得到解密函数的运算结果的一个字节：

• 解密函数运算结果的最后一个字节的数值（Tn[15]）。

由于明文字节（Pn'[15]）是密文字节（Cn-1'[15]）和解密函数运算中间结果字节（Tn[15]）的异或运算结果，那么知道了明文字节（Pn'[15]）和密文字节（Cn-1'[15]），使用异或运算的归零律和恒等律，计算出解密函数运算中间结果字节（Tn[15]）就是一件简单的事情了。

> Pn'[15] = Tn[15] ^ Cn-1'[15]

> =>

> Pn'[15] ^ Cn-1'[15] = Tn[15] ^ Cn-1'[15] ^ Cn-1'[15] = Tn[15]

既然知道了解密函数运算中间结果字节Tn[15]）和原始密文分组的字节，真正的明文字节也就被破解出来了。

> Pn[15] = Tn[15] ^ Cn-1[15]

你看，非常简单的运算，运算次数不多于255次，攻击者就破解了一位字节。接下来的目标，就是破解倒数第二位字节。

破解倒数第二位字节，要使用的补齐数据是一（0x01）。首先，既然攻击者已经知道了最后一个字节的明文、密文以及解密函数运算的中间结果，他就可以计算、修改上一次的密文分组的最后一个字节，使得解密后的明文分组的最后一个字节是一。

> Tn[15] ^ Cn-1'[15] = 0x01

> =>

> Tn[15] ^ Cn-1'[15] ^ Tn[15] = 0x01 ^ Tn[15]

> Cn-1'[15] = 0x01 ^ Tn[15]

这样，解密端就确认了最后一个字节是一，也就是补齐数据的标识字节是一。只要倒数第二个字节也是一，补齐数据的检验就通过了。倒数第二个字节破解方式和第一个字节的破解方式相同。

每个字节的破解，运算次数都不会多于255次。从倒数第一位开始，依次破解，直到第一个字节破解结束，总的计算量是255乘以字节数。对于AES而言，一个数据分组有16个字节，破解计算只需要255 * 16 = 4080次。

这么小的破解计算量，是没有什么安全性可说的。预测补齐数据的这一类破解方案，都可以叫做“补齐预言攻击”。2002年，塞尔吉·沃德奈（Serge Vaudenay）公布了补齐预言攻击。

有一些2002年之前制定的安全协议，不能很好地应对这种攻击方案。相应地，也有一些成功的破解方案。那么，2002年以后的年月呢？CBC模式该怎么规避补齐预言攻击？

有效的方式有两个。第一个方式，也是最有效的方式，就是和数据完整性校验的算法结合起来，而不是依赖补齐数据是否合法，来判断解密数据是不是有效。这种方式，我们讨论数据完整性校验算法的时候，还会再讨论。另外一种方式，就是在初始化向量上想办法。

初始化向量就用一次吗？

初始化向量，现在你应该很熟悉了，就是加密或者解密运算开始的时候使用的向量。这个变量不是就使用一次、改变一次而已吗？怎么还使用它来阻断补齐预言攻击呢？

如果这个变量就使用一次、改变一次，它的确起不到作用。我们要做的，就是要改变这种一次性使用的方式，变成多次使用的方式。是不是听起来有点难度？是有难度的。

如果加密端和解密端每次运算（一次运算可以包含多个数据分组）都重置初始化向量，并且使用不一样的初始化向量。只要使用了不一样的初始化向量，每一次运算的最后一个密文分组都是不同的。这样，就不能重复地使用这个密文分组反复运算，从而切断了补齐预言攻击的攻击路径。

稍微有点麻烦的是，解密端怎么才能判断每一次运算都使用了不同的初始化向量。这不是一个容易的事情。所以，如果仅仅依靠一次运算一个初始化向量的办法，也很难有成熟的解决方案。

一次运算一个初始化向量的办法，除了可以用来阻断补齐预言攻击之外，它还有一个很有吸引力的特点。不过，让我们下一次再接着讨论。

Take Away（今日收获）

今天，通过讨论怎么在CBC模式的解密端，利用数据补齐方案，来展开补齐预言攻击，我们知道了数据补齐方案可能存在的缺陷。

另外，我们还讨论了阻断补齐预言攻击的办法，那就是，每一次加密/解密计算，都使用初始化向量，而不是仅仅就使用一次初始化向量。

通过今天的讨论，我们要：

• 知道CBC模式存在补齐预言攻击；
• 知道使用不同初始化向量的来阻断补齐预言攻击。

思考题

今天的思考题，我们去看一看协议的设计。

在TLS 1.2的设计中，使用CBC模式加密的数据包是由一个明文的初始化向量和密文的加密数据组成的。明文的初始化向量和密文的加密数据，可以通过不安全的网络，传递给信息接收方。

第一个问题是：为什么我们可以传递明文的初始化向量？

第二个问题是，为什么要传递初始化向量？

另外，如果你仔细看下面的数据结构，就会注意到，在TLS 1.2的设计里，待加密的数据块，已经补齐到算法要求的数据块的整数倍了。这似乎也就意味着，上一个数据包和这一个数据包，以及这一个数据包和下一个数据包，都可以无缝地衔接，而不需要使用数据补齐，也不需要每次都使用一个初始化向量。

既然已经补齐了，为什么还要每一次加密都使用一个初始化向量？这是第三个问题。

理解了这三个问题，你就算学会使用CBC算法了。CBC算法要被扫进垃圾箱的主要原因，就是因为这个算法太难用对了，虽然它是用途最广泛的加密模式。如果你可以用对它，在很多场景，它还是能够再延续使用一段时间，等待你升级到更皮实的算法。

struct {
  opaque IV[SecurityParameters.record_iv_length];
  block-ciphered struct {
      opaque content[TLSCompressed.length];
      opaque MAC[SecurityParameters.mac_length];
      uint8 padding[GenericBlockCipher.padding_length];
      uint8 padding_length;
  };      
} GenericBlockCipher;

欢迎在留言区留言，记录、讨论你的理解和看法。

好的，今天就这样，我们下次再聊。