你好,我是范学雷。
到目前为止,你已经跟我一起走了很长的路了。不知道这一路上,你有了哪些心得和体会?对密码学是不是多了很多新的认知和想法?这一讲,我们继续上路,踏足密码学的世界。
前几讲,我们花了很长时间讨论了对称密钥的算法,以及使用对称密钥算法要注意哪些陷阱。但是,不知道你有没有注意到,一直有一个悬而未决的问题。
我们要使用对称密钥算法,总得有对称密钥吧。那么,对称密钥是从哪儿来的?这是我们这一次要讨论的问题。
对称密钥从哪里来的?在讨论这个问题之前,我们先要弄清楚另外一个问题。一个合格的对称密钥,应该满足什么样的条件呢?只有知道了需求,我们才能有解决的方案。
还记得我们之前提到过的AES-128和AES-256算法吗?
其中的128和256,指的是密钥的长度。也就是说,AES-128需要128位的密钥,AES-256需要256位的密钥。一般来说,一个对称密钥算法的密钥长度是固定的。这就是对称密钥的第一个要求:对称密钥的长度是由对称密钥算法确定的。
当然,这并不意味着一个对称密钥只能用于一个加密算法。一个对称密钥,一般可以用于任意一个对称密钥算法,只要这个对称密钥满足算法要求的密钥长度。比如一个256位的对称密钥,既可以用于AES-256,也可以用于ChaCha20。
可是,一个对称密钥用于两个不同算法,这不是我们推荐的用法。因为,我们要考虑算法破解的风险。如果一个算法被破解了,那么它使用的对称密钥可能也就被破解了。我们不希望一个算法的失败连累另一个算法要保护的数据。
所以,大部分的应用程序接口,都不会限制一个对称密钥只能用于一个算法。但是,我们要有意识地避免这种情况。比如说,如果一个对称密钥已经用于AES-256的加密计算了,就不要再把它用于ChaCha20或者其他的加密算法了。
说完了对称密钥的长度,我们来看对称密钥的强度。
有印象的话,你应该记得AES-128算法的安全强度是128位,AES-256算法的安全强度是256位。可是,如果没有高质量的对称密钥,这样的安全强度就没有意义。
举个例子,如果密钥只能是阿拉伯数字,那么128位的密钥就只有10^16种可能性。也就是,如果使用蛮力攻击的话,最多需要10^16次尝试,加密密钥就能够找到,加密数据就能够被破解。
如果我们把10^16转换成按位表示的安全强度,也不过就是53位的安全强度,这离128位的安全强度可相差太远了。所以,对称密钥的强度一定要和加密算法的强度匹配。比如说吧,AES-128算法需要128位的密钥,这个密钥就要有128位的强度。
对于任意给定的密钥,我们并不一定能够判断它的强度是不是足够。比如说,我们并不能判断“123456”是不是比“135246”强度更大。所以,当我们说密钥强度的时候,其实我们关注的还有产生密钥的机制。
首先,产生密钥的机制要有匹配的强度。如果产生密钥的机制只有128位的安全强度,它就不能提供256位安全强度的密钥。简单地说,攻击产生密钥的机制就可以了。
其次,密钥在它的长度上要均匀分布。也就是说,这个密钥的每一位是0还是1的概率都是50%。如果不能做到均匀分布,就会降低密钥的安全性。比如说,我们前面提到的阿拉伯数字的密钥,就是密钥没有做到均匀分布,导致安全强度降低的例子。
还有,密钥生成机制产生的密钥要随机。也就是说,下一个密钥要均匀分布,而且不可预测。如果下一个密钥不是随机的,那么下一个密钥的安全性就没有保障。如果上一个密钥是“123456”,下一个密钥是“123457”,只是简单地递增,那么这两个密钥都是不合格的密钥。
总结起来就是,一个合格的对称密钥,它的长度和强度要与对称密钥算法相匹配。
在第6讲,我们提到,密钥的保密性和算法的安全性是对称密钥算法安全的两个关键因素。
既然密钥需要保密,那当然也就意味着密钥有秘可保。没有秘密的密钥当然谈不上保密,不能保密的密钥也没法保护数据的机密性。总之,对称密钥要有秘密。
不过,需要注意的是,秘密也是有安全强度的。比如说,很多地方的民俗,有“猜有无”的酒令。猜的人猜测对方握紧的手里有没有东西。
对于出酒令的人来说,手里有没有东西,当然是一个秘密。但是这个秘密被猜中的几率是50%。如果换算成密码学的指标,也就是只有1位的安全强度。1位的安全强度,当然简单好玩,适合于饮酒助兴。可是只有1位的安全性,并不适合在计算机系统中保护我们的机密数据。
一个合格的对称密钥,要有足够的秘密,并且它的长度和强度要与对称密钥算法相匹配。
这三个需求看起来简单、直观,但是用起来很容易就掉进强度错配、无秘可保的坑里。好了,有了这三个需求,对称密钥从哪里来这个问题,我们就可以来一起讨论它了。
那么,对称密钥是从哪里来的呢?你可能觉得这个问题有点怪怪的,其实这个问题,换个说法,就是我们去哪里才能够找到长度和强度都符合要求的秘密?
先看秘密的来源,来源主要有两类:
对应地,也就是对称密钥的两种来源。
计算机用户持有的秘密,主要表现为只有该用户知道的秘密和只有该用户拥有的秘密两种。比如,我们能够记住的用户口令,是只有我们知道的秘密;我们的指纹,是只有我们拥有的信息。
遗憾的是,我们能够记住的密码很短,一般来说,满足不了对称密钥强度的需求;我们拥有的指纹、面容、虹膜信息,都可以复制,保守这样的秘密是一个极具挑战的任务。陌生的场合,我们摸一摸杯子,睁一睁眼睛,露一下面颊,这些所谓的秘密就都不再是秘密了。
我们拥有的生物特征不可靠,我们能够记住的又太少,那为什么指纹识别和用户密码还这么流行呢?主要原因是还是没有更好的、更简单的办法。
从我接触密码学开始,就已经有人喊口令要消亡了。二十多年了,口令依然活得有模有样,指纹/面部识别也越来越流行,尤其是需要身份认证的时候。
既然口令的强度不够,那如果一段加密数据,只有用户参与才能解密,那该怎么办呢?解决的办法就是分级:使用弱的口令来保护强的密钥,然后使用强的密钥来保护私密数据。
如果加密数据泄漏了,由于保护它的对称密钥有足够的强度,我们不用担心破解的问题。
而口令,主要用于身份认证和衍生密钥。身份认证和密钥衍生,都不是高频次的运算。 从口令推导出来的对称密钥也不保存、不长留。这些措施,都降低了口令破解带来的数据泄漏风险。

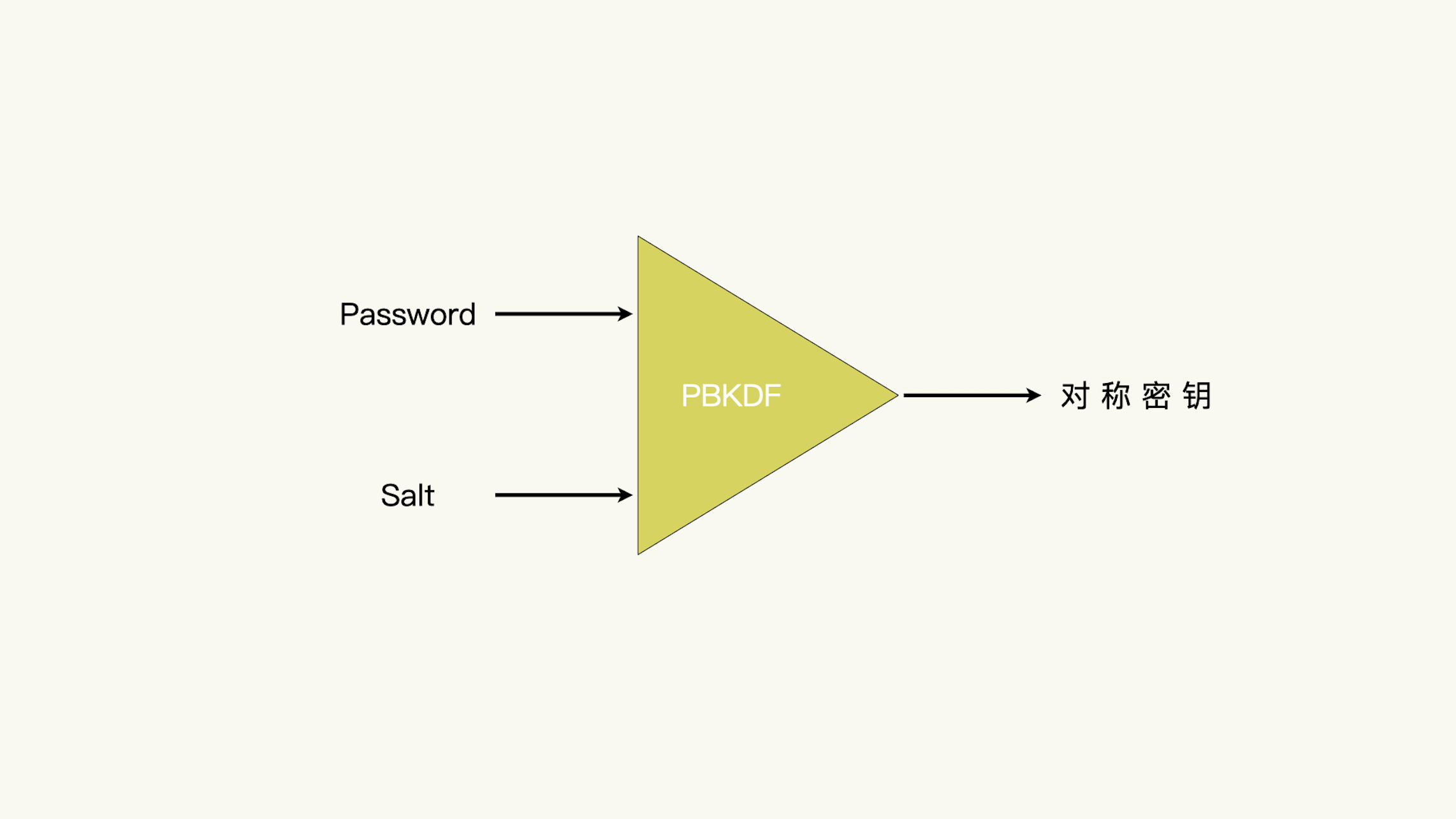
使用口令生成对称密钥的办法,通常成为“基于口令的密钥推导”。现在常用的基于口令的密钥推导算法是PBKDF2。我不在这里讲这个算法的细节了,你可以自己去找一找相关的规范。
不过,我们需要注意的是,由于口令的安全强度不够,很容易被破解,我们需要经常地变换口令,有些公司是强制性要求。如果口令变换了,从它衍生出来的对称密钥当然也就随着变换了。
如果我们直接使用衍生出来的对称密钥加密数据,每次的口令变化,都需要把已经加密的数据重新加密一遍。这可不是好事情!
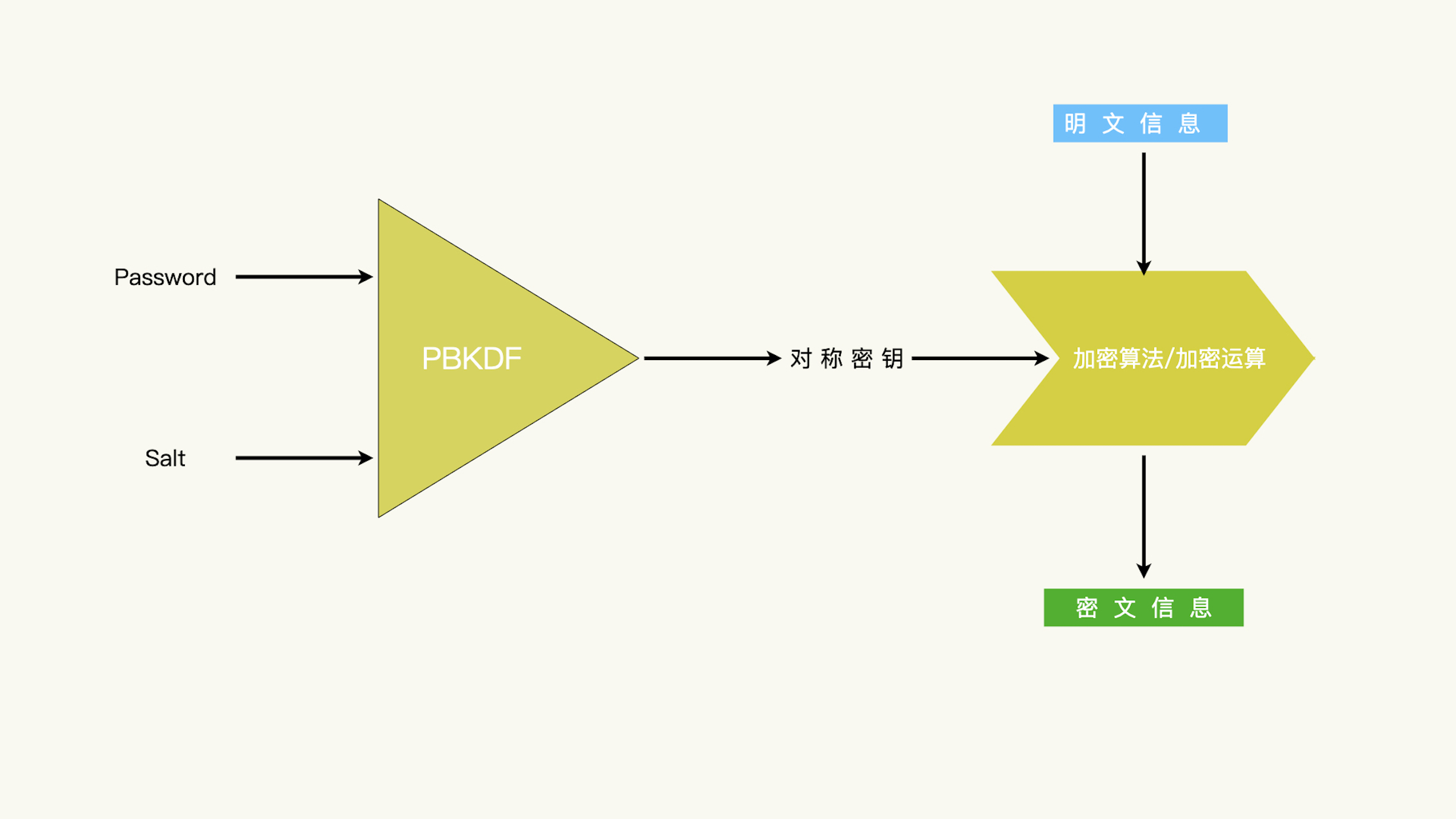
所以,通常地,我们也不推荐使用口令推导出来的密钥直接加密需要留存的数据。有什么办法克服这个障碍呢?解决这个问题,我们还要再添加一个环节。也就是使用推导出的密钥保护一个使用时间更长的密钥;而使用时间更长的密钥用来保护私密数据。
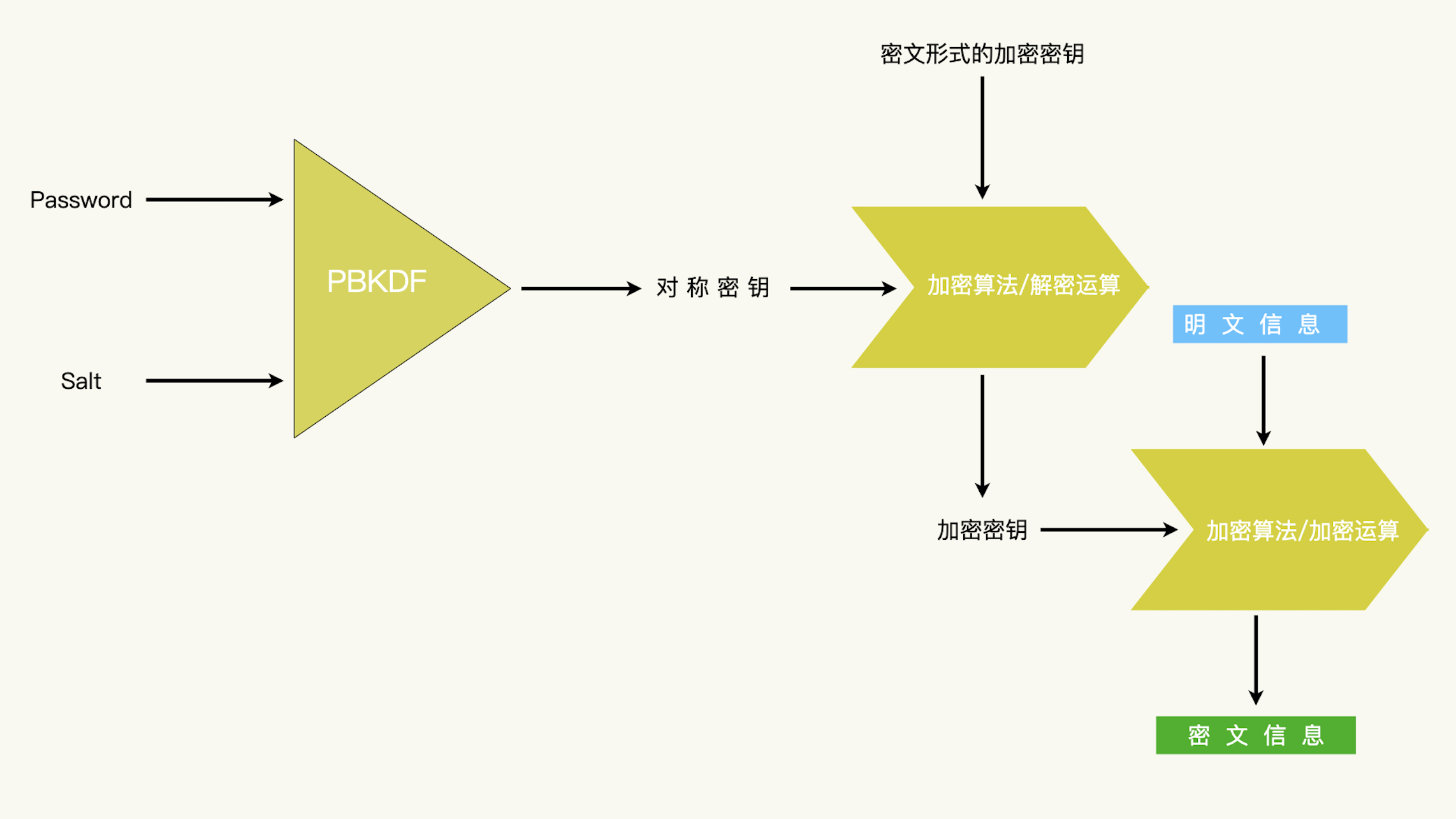
多了一个环节以后,如果口令发生变更,我们只需要重新加密留存的对称密钥就行了,而不需要改动已经加密了的数据。那么,这个使用时间更长的密钥是怎么来的呢?
这就需要我们讨论下一个秘密的来源了:计算机持有的秘密。
计算机持有的秘密,主要用的是我们上一节所讨论的随机数。
由于随机数是不可预测的,我们只要把随机数当做秘密信息来保护,就没有其他的人或者其他的计算机能够知道这个秘密。这样看起来,随机数能够完美地契合对称密钥的需求,无论是长度强度,还是保密要求。
需要一个对称密钥的时候,如果我们知道需要的长度、强度,找对强度匹配的随机数发生器,生成一个对应长度的随机数,就可以获得一个对称密钥了。这是一个看起来很简单、直观的办法。
但是,计算机持有的秘密也有一个缺陷,就是没法转换成我们人脑能够记住的东西。我们没有办法记住随机数,更没有办法记住从随机数衍生出来的对称密钥。既然我们没有办法,解密还需要对称密钥,那就需要计算机替我们记住它。
计算机该怎么管理对称密钥,怎么保守密钥秘密?这些问题也就一下子都冒出来了。
正像我们讨论过的一样,使用口令推导出的密钥可以保护使用时间更长的密钥,当然也包括使用随机数生成的密钥。不过这种保护方式,也有很大的局限性。这种局限性又在哪里呢?还有没有其他的方式?这些问题,我们下一次再讨论。
今天,我们讨论了一个合格的对称密钥应该满足什么条件,以及对称密钥的两个主要来源。
通过今天的讨论,我们要:
好的,又到了留思考题的时候了。
今天的思考题,我们稍微加大一点难度。不过也不用紧张,我相信只要你去反复撕扯这个问题,不管结论是什么,你都会有收获的。
我们反复强调过,我们能够记住的东西很少,我们能够记住的口令的安全强度也远远不够。那为什么从口令推导出来的密钥就能够更安全呢? 如果口令只有6位数字,猜中口令的可能性是10^6。
转换成按位表示的安全强度,也不过就是20位的强度。这样的安全强度我们应该担心吗?如果这样的担忧是合理的,我们应该怎么提高口令的安全性?如果使用从口令推导出来的密钥,需要注意哪些问题?
欢迎在留言区留言,分享你的经验。参与讨论的人越多,我们互相学习、互相启发,能够得到的就越多。
好的,今天就这样,我们下次再聊。
元旦快乐!
评论