下列代码是在《雷神之锤III竞技场》源代码中的一个函数（已经剥离了C语言预处理器的指令）。其实，最早在2002年（或2003年）时，这段平方根倒数速算法的代码就已经出现在Usenet与其他论坛上了，并且也在程序员圈子里引起了热烈的讨论。

我先把这段代码贴出来，具体如下：

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y  = number;
    i  = * ( long * ) &y; // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );  // what the fuck? 
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );  // 1st iteration 
    // 2nd iteration, this can be removed
    // y  = y * ( threehalfs - ( x2 * y * y ) ); 

    return y;
}

这段代码初读起来，我是完全不知所云，尤其是那个魔数0x5f3759df，根本不知道它是什么意思，所以，注释里也是 What the fuck。今天的这篇文章里，我主要就是想带你来了解一下这个函数中的代码究竟是怎样出来的。

其实，这个函数的作用是求平方根倒数，即$x^{-1/2}$，也就是下面这个算式：

$$\frac{1}{\sqrt{x}}$$

当然，它算的是近似值。只不过这个近似值的精度很高，而且计算成本比传统的浮点数运算平方根的算法低太多。在以前那个计算资源还不充分的年代，在一些3D游戏场景的计算机图形学中，要求取照明和投影的光照与反射效果，就经常需要计算平方根倒数，而且是大量的计算——对一个曲面上很多的点做平方根倒数的计算。也就是需要用到下面的这个算式，其中的x,y,z是3D坐标上的一个点的三个坐标值。

$$\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}$$

基本上来说，在一个3D游戏中，我们每秒钟都需要做上百万次平方根倒数运算。而在计算硬件还不成熟的时代，这些计算都需要软件来完成，计算速度非常慢。

我们要知道，在上世纪90年代，多数浮点数操作的速度更是远远滞后于整数操作。所以，这段代码所带来的作用是非常大的。

计算机的浮点数表示

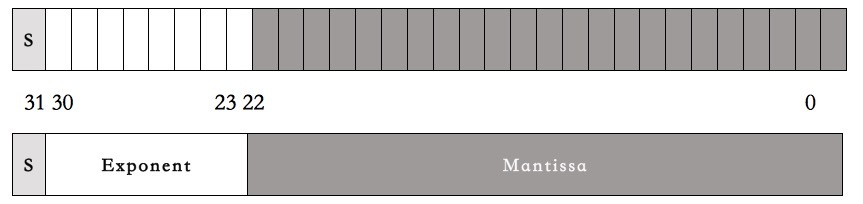
为了讲清楚这段代码，我们需要先了解一下计算机的浮点数表示法。在C语言中，计算机的浮点数表示用的是IEEE 754 标准，这个标准的表现形式其实就是把一个32bits分成三段。

第一段占1bit，表示符号位。代称为S（sign）。
第二段占8bits，表示指数。代称为E（Exponent）。
第三段占23bits，表示尾数。代称为M（Mantissa）。

如下图所示：

然后呢，一个小数的计算方式是下面这个算式：

$$(-1)^{S}\ast(1+\frac{M}{2^{23}})\ast 2^{(E-127)}$$

但是，这个算式基本上来说，完全就是让人一头雾水，摸不着门路。对于浮点数的解释基本上就是下面这张漫画里表现的样子。

下面，让我来试着解释一下浮点数的那三段表示什么意思。

第一段符号位。对于这一段，我相信应该没有人不能理解。
第二段指数位。什么叫指数？也就是说，对于任何数x，其都可以找到一个$n$，使得$2^{n}$<=x<=$2^{n+1}$。比如：对于3来说，因为 2 < 3 < 4，所以 n=1。而浮点数的这个指数为了要表示0.00x的小数，所以需要有负数，这8个bits本来可以表示0-255。为了表示负的，取值要放在 [-127,128] 这个区间中。这就是为什么我们在上面的公式中看到的 $2^{(E-127)}$这一项了。也就是说，$n = E-127$，如果$n=1$，那么$E$就是128了。
第三段尾数位。也就是小数位，但是这里叫偏移量可能好一些。这里的取值是从[ 0 - $2^{23}$]中。你可以认为，我们把一条线分成$2^{23}$个线段，也就是8388608个线段。也就是说，把$2^{n}$到$2^{n+1}$分成了8388608个线段。而存储的M值，就是从$2^n$到 x 要经过多少个段。这要计算一下，$2^{n}$到x的长度占$2^{n}$到$2^{n+1}$长度的比例是多少。

我估计你对第三段还是有点不懂，那么我们来举一个例子。比如说，对3.14这个小数。

是正数。所以，S = 0
$2^1$ < 3.14 <$2^2$。所以，n=1， n+127 = 128。所以，E=128。
(3.14 - 2) / (4 - 2) = 0.57，而$0.57*2^{23} = 4781506.56$，四舍五入，得到M = 4781507。因为有四舍五入，所以，产生了浮点数据的精度问题。

把S、E、M转成二进制，得到 3.14的二进制表示。

我们再用IEEE 754的那个算式来算一下：

$${(-1)}^0*({1+\frac{4781507}{2^{23}}})*2^{(128-127)}$$

$$1*(1+0.5700000524520874)*2$$
$$=3.1400001049041748046875$$

你看，浮点数的精度问题出现了。

我们再来看一个示例，小数 0.015。

是正数。所以，S = 0。
$2^{-7}< 0.015 < 2^{-6}$ 。所以，n=-7， n+127 = 120。所以，E=120。
$ (0.015 - 2^{-7}) / (2^{-6} - 2^{-7}) $ = $0.0071875/0.0078125=0.92$。而$0.92 * 2^{23} = 7717519.36$，四舍五入，得到 M = 7717519。

于是，我们得到0.015的二进制编码：

其中：

120 的二进制是01111000
7717519的二进制是11101011100001010001111

返回过来算一下：

$$(-1)^{0}\ast (1+\frac{7717519}{2^{23}})\ast 2^{(120-127)}$$

$$(1+0.919999957084656)*0.0078125$$
$$=0.014999999664724$$

你看，浮点数的精度问题又出现了。

我们来用C语言验证一下：

int main() {
    float x = 3.14;
    float y = 0.015;
    return 0;
}

在我的Mac上用lldb 工具 Debug 一下。

(lldb) frame variable
(float) x = 3.1400001
(float) y = 0.0149999997

(lldb) frame variable -f b
(float) x = 0b01000000010010001111010111000011
(float) y = 0b00111100011101011100001010001111

从结果上，完全验证了我们的方法。

好了，不知道你看懂了没有？我相信你应该看懂了。

简化浮点数公式

因为那个浮点数表示的公式有点复杂，我们简化一下：

$$(-1)^{S}\ast (1+\frac{M}{2^{23}})\ast 2^{(E-127)}$$

我们令，$m = (\frac{M}{2^{23}} )$，$e = (E-127)$。因为符号位在$y= x^{-\frac{1}{2}}$的两端都是0（正数），也就可以去掉，所以浮点数的算式简化为：

$$(1+m)\ast2^{e}$$

上面这个算式是从一个32bits二进制计算出一个浮点数。这个32bits的整型算式是：

$$M+E\ast2^{23}$$

比如，0.015的32bits的二进制是：00111100011101011100001010001111，也就是整型的：

$$7717519+120\ast 2^{23}$$
$$= 1014350479$$
$$= 0X3C75C28F$$

平方根倒数公式推导

下面，你会看到好多数学公式，但是请你不要怕，因为这些数学公式只需要高中数学就能看懂的。

我们来看一下，平方根数据公式：

$$y=\frac{1}{\sqrt[2]{x}}=x^{-\frac{1}{2}}$$

等式两边取以2为基数的对数，就有了：

$$\log_2(y) =-\frac{1}{2}\log_2(x)$$

因为我们实际上在算浮点数，所以将公式中的 x 和 y 分别用浮点数的那个浮点数的简化算式$ (1+ m)*2^e$替换掉。代入$\log()$公式中，我们也就有了下面的公式：

$$\log_{2} (1+m_y)+e_y$$
$$=-\frac{1}{2}(\log_2(1+m_x)+e_x)$$

因为有对数，这公式看着就很麻烦，似乎不能再简化了。但是，我们知道，所谓的$m_x$或是$m_y$，其实是个在0和1区间内的小数。在这种情况下，$\log_2 (1.x)$接近一条直线。

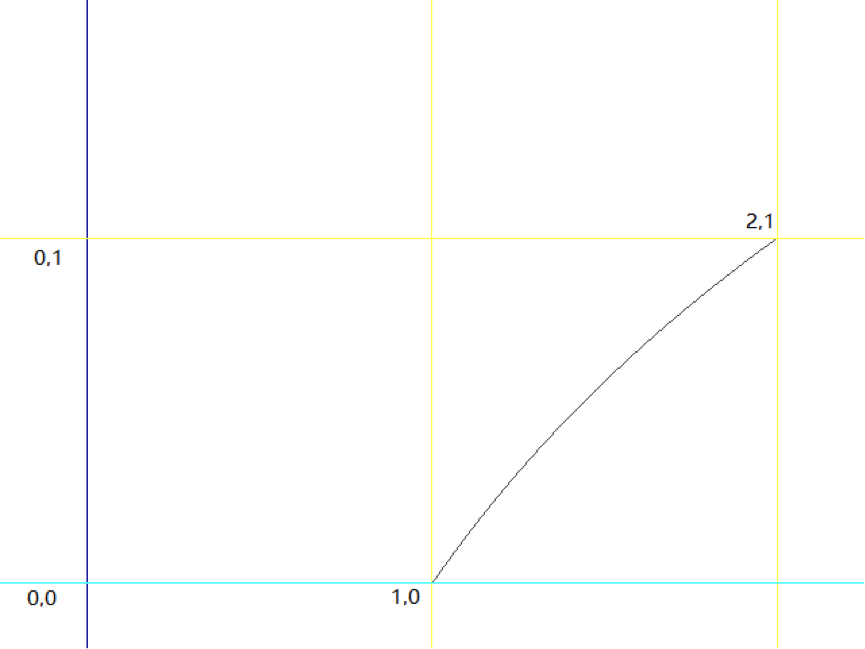
那么我们就可以使用一个直线方程来代替，也就是：

$$\log_{2}(1+m)\approx m+\sigma $$

于是，我们的公式就简化成了：

$$m_y+\sigma+e_y\approx-\frac{1}{2}(m_x+\sigma+e_x)$$

因为$m = (\frac{M}{2^{23}})$，$e = (E-127)$，代入公式，得到：

$$\frac{M_y}{2^{23}}+\sigma+E_y-127$$
$$\approx-\frac{1}{2}(\frac{M_x}{2^{23}}+\sigma+E_x-127)$$

移项整理一下，把 σ 和127 从左边，移到右边：

$$\frac{M_y}{2^{23}}+E_y\approx-\frac{1}{2}(\frac{M_x}{2^{23}}+E_x)-\frac{3}{2}(\sigma-127)$$

再把整个表达式乘以$2^{23}$，得到：

$${M_y}+E_y{2^{23}}$$
$$\approx-\frac{1}{2}(M_x+E_x{2^{23}})-\frac{3}{2}(\sigma-127){2^{23}}$$

可以看到一个常数：$-\frac{3}{2}(\sigma-127){2^{23}}$，把负号放进括号里，变成$\frac{3}{2}(127-\sigma){2^{23}}$，并可以用一个常量代数R来取代，于是得到公式：

$${M_y}+E_y{2^{23}}\approx R-\frac{1}{2}(M_x+E_x{2^{23}})$$

还记得我们前面那个“浮点数32bits二进制整型算式” $M+E* 2^{23}$吗？假设，浮点数x的32bits的整型公式是：$I_x= M_x+ E_x 2^{23}$，那么上面的公式就可以写成：

$$I_y\approx R-\frac{1}{2}I_x$$

代码分析

让我们回到文章的主题，那个平方根函数的代码。

首先是：

i  = * ( long * ) &y; // evil floating point bit level hacking

这行代码就是把一个浮点数的32bits的二进制转成整型。也就是，前面我们例子里说过的，3.14的32bits的二进制是：01000000010010001111010111000011，整型是：1078523331。即y = 3.14，i = 1078523331。

然后是：

i  = 0x5f3759df - ( i >> 1 );  // what the fuck?

这就是：

i  = 0x5f3759df - ( i / 2 );

也就是我们上面推导出来的那个公式：

$$I_y\approx R-\frac{1}{2}I_x$$

代码里的 R = 0x5f3759df。

我们又知道，R = $\frac{3}{2}(127-\sigma){2^{23}}$，把代码中的那个魔数代入，就可以计算出来：σ= 0.0450465 。这个数是个神奇的数字，这个数是怎么算出来的，现在还没人知道。不过，我们先往下看后面的代码：

    x2 = number * 0.5F;
    y  = * ( float * ) &i;
    y  = y * ( threehalfs - ( x2 * y * y ) );  // 1st iteration 
    // 2nd iteration, this can be removed
    // y  = y * ( threehalfs - ( x2 * y * y ) );

这段代码相当于下面这个公式：

$$I_{y’} = I_y(1.5-0.5 x I_y^2)$$

这个其实是“牛顿求根法”，这是一个为了找到一个 f(x)= 0 的根而用一种不断逼近的计算方式。请看下图：

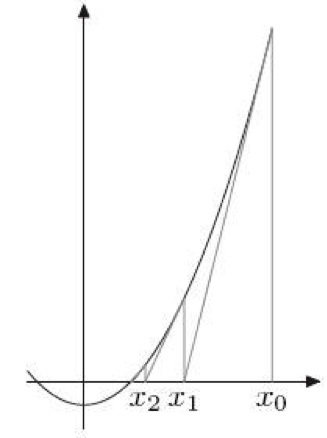
首先，初始值为X0，然后找到X0所对应的Y0（把X0代入公式得到Y0 = f(X0)），然后在（X0,Y0）这个点上做一个切线，得到与X轴交汇的X1。再用X1做一次上述的迭代，得到X2，就这样一直迭代下去，一直找到，y = 0时，x的值。

牛顿法的通用公式是：

$$x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}$$

于是，对于$y= \frac{1}{\sqrt{x}}$来说，对固定的x（常数），我们求y使得$\frac{1}{y^2}-x=0$，$f(y)= \frac{1}{y^2} -x$ , $f’(y)=\frac{-2}{y^3}$ 。注意：$f’(y)$是$f(y)$关于y的导数。

代入上述的牛顿法的通用公式后得到：

$$y_{n+1}=y_n-\frac{\frac{1}{y_n^2}-x}{\frac{-2}{y_n^3}}$$
$$=\frac{y_n(3-xy_n^2)}{2}=y_n(1.5-0.5xy_n^2)$$

正好就是我们上面的代码。

整个代码是，之前生成的整数操作产生首次近似值后，将首次近似值作为参数送入函数最后两句进行精化处理。代码中的两次迭代正是为了进一步提高结果的精度。但由于《雷神之锤III》的图形计算中并不需要太高的精度，所以代码中只进行了一次迭代，二次迭代的代码则被注释了。

计算机的浮点数表示

简化浮点数公式

平方根倒数公式推导

代码分析

相关历史