
你好,我是宫文学。
我们前面几节课,讲的都是编译器前端的功能。虽然,要实现完善的前端功能,我们要做的工作还有很多。不过,我们现在已经不“虚”了!因为我们已经把编译器前端部分的主要知识点都讲得差不多了,其他的我们可以慢慢完善。
所以,现在我们重新把精力放回到编译器后端功能和运行时上来,这部分的功能我们还有待加强。在第一部分起步篇中,为了尽量简化实现过程,我们的语言只支持了整数的运算,甚至都没区分整型的长度,统一使用了32位的整型。
但这在实用级的语言中可行不通,我们还需要在里面添加各种丰富的数据类型。所以,接下来,我们会花几节课的时间,丰富一下我们语言支持的数据类型。首先我们会添加一些内置的基础类型,比如浮点型、字符串和数组。之后,我们还要通过对面向对象编程特性,支持用户自定义自己的类型。
在这一节课,我们先来看一下如何让我们的语言支持浮点型数据。为实现这个目的,我们需要先了解CPU为了支持浮点数有哪些特别的设计,ABI方面又有一些什么规定,以及如何修改汇编代码生成逻辑。而且,为了正确地在汇编代码中表示浮点型字面量,你还会学到浮点数编码方面的国际标准。
首先,让我们了解一下CPU硬件和ABI对浮点数运算提供的支持。
我们先来回顾一下起步篇中关于整数运算的知识。已经有些日子没见到它们了,不知道你还记不记得?你可以和下面我们重点讲解的浮点数的处理模式对比着来看,看看它们有怎样的不同,这也能加强你对这些重点知识的记忆。
X86架构的CPU在64位模式下对整数运算的支持,最重要的就是这两个知识点:
另外,ABI也针对整数运算做了一些规定,比如:
那么,我们再来看看CPU对浮点数运算的支持是怎么样的。
其实,最早期的X86CPU只支持整数运算,并不支持浮点数运算。如果我们要进行浮点数运算,就要用整数运算来模拟。但是这样的话,浮点数运算的速度就会比较慢。
而现代CPU解决了这个问题,普遍从硬件层面进行浮点运算,所以编译器也要直接生成浮点运算的机器码,最大程度地发挥硬件的性能。
我们之前说过,一款CPU可能支持多个指令集。而某些指令集,就是用于支持浮点数计算的。在X86的历史上,CPU最早是通过一个协处理器来处理浮点数运算,这个协处理器叫做FPU(浮点处理单元),它采用的指令集叫做X87。后来这个协处理器就被整合到CPU中了。
再后来,为了提高对多媒体数据的处理能力,厂商往CPU里增加了新的指令集,叫做MMX指令集。MMX的具体含义,有人说是多媒体扩展(MultiMedia eXtension),有人说是矩阵数学扩展(Matrix Math eXtension)。不管缩写的含义是什么,MMX主要就是增强了对浮点数的处理能力,因为多媒体的处理主要就是浮点数运算。
并且,MMX还属于SIMD类型的指令集。SIMD(Single Instruction Multiple Data)是一条指令对多个数据完成加减乘数运算的意思,因此MMX指令能让CPU的处理效率更高。
MMX指令集后来又升级成为了SSE指令集,还形成了多个版本,每个版本都会增加一些新的指令和功能。最新的版本是SSE4.2。SSE是流式SIMD扩展(Streaming SIMD Extensions)的意思。到今天,X86计算机进行浮点数运算的时候,基本上都是采用SSE指令集,不再使用x87指令集,除非是使用那些特别早的型号的CPU。
不知道你还记不记得,我们之前提过,你可以查询自己电脑的CPU所支持的指令集。在macOS上,我用下面的命令就可以查到:
sysctl machdep.cpu.features machdep.cpu.leaf7_features
然后你会在命令行终端,得到关于CPU特性的信息。这些特性就对应着指令集。比如,出现在第一个的FPU,就对应着X87指令集。你也会从其中看到多个版本的SSE指令集。

如果你嫌上面的命令太长,那也可以使用一个短一点的命令。这个命令会打印出更多关于CPU的信息,比如CPU所支持的线程数,等等。其中也包括该CPU的指令集。
sysctl machdep.cpu
这里我插一个小知识点,不知道你会不会有这个疑惑,我们操作系统是怎么知道某CPU支持哪些指令集的呢?原来,X86架构的CPU提供了一个cpuid指令。你用这个指令就可以得到CPU类型、型号、制造商信息、商标信息、序列号、缓存,还有支持特性(也就是指令集)等一系列信息了。所以你看,要理解软件的功能,经常都需要底层硬件架构的知识。
好了,既然我们需要用到SSE指令集,那就需要了解一下SSE指令集的特点。并且,SSE其实不仅能处理浮点数,还能处理整数。不过现在我们主要关心与浮点数有关的特性。这些信息从哪里获得呢?当然是从Intel的手册。下面这些信息就来自于《Intel® 64 and IA-32 Architectures Software Developer’s Manual,Volume 1: Basic Architecture》,我给你稍微总结一下。
首先,我们看看SSE指令所使用的寄存器。
在64位模式下,SSE可以使用16个128位的寄存器,分别叫做xmm0~xmm15。
此外,SSE还会使用一个32位的MXCSR寄存器,用于保存浮点数运算时的控制信息和状态信息。比如,如果你做除法的时候,除数是0,那么就会触发一个异常。而MXCSR寄存器上的某个标志位会决定如何处理该异常:是采用内置的标准方法来处理呢,还是触发一个软件异常来处理。关于MXCSR的详细信息,你可以按需要查看一下手册。
第二,我们看一下SSE对数据类型的支持。
SSE指令支持32位的单精度数,也支持64位的双精度数。不过,单精度数和双精度数的格式,都遵循IEEE 754标准。
在SSE指令中,寄存器里可以只放一个浮点数,这个时候我们把它叫做标量(Scalar)。还可以把多个浮点数打包放在一个寄存器里,这种数据格式叫做打包格式( Packed Data Types),或者叫做向量格式。下图就显示了在一个128位寄存器里存放4个单精度浮点数的情况。

打包格式是用于SIMD类型的指令的,这样一条指令就能处理寄存器里的4个单精度浮点数的计算。不过,我们关注的还是对标量数据的处理,所以就先忽略向量数据处理的情况,有需要我们再补充。
第三,我们看看SSE指令的情况。
SSE对处理浮点数的指令,包括向量指令和标量指令。另外,在JavaScript中,number是以双精度数来表示的,所以我们的语言也就可以忽略与单精度浮点数有关的指令,直接关注双精度浮点数指令就好了。
我在下面这张表中,列出了SSE中与标量的、双精度浮点数处理有关的一些主要的指令:
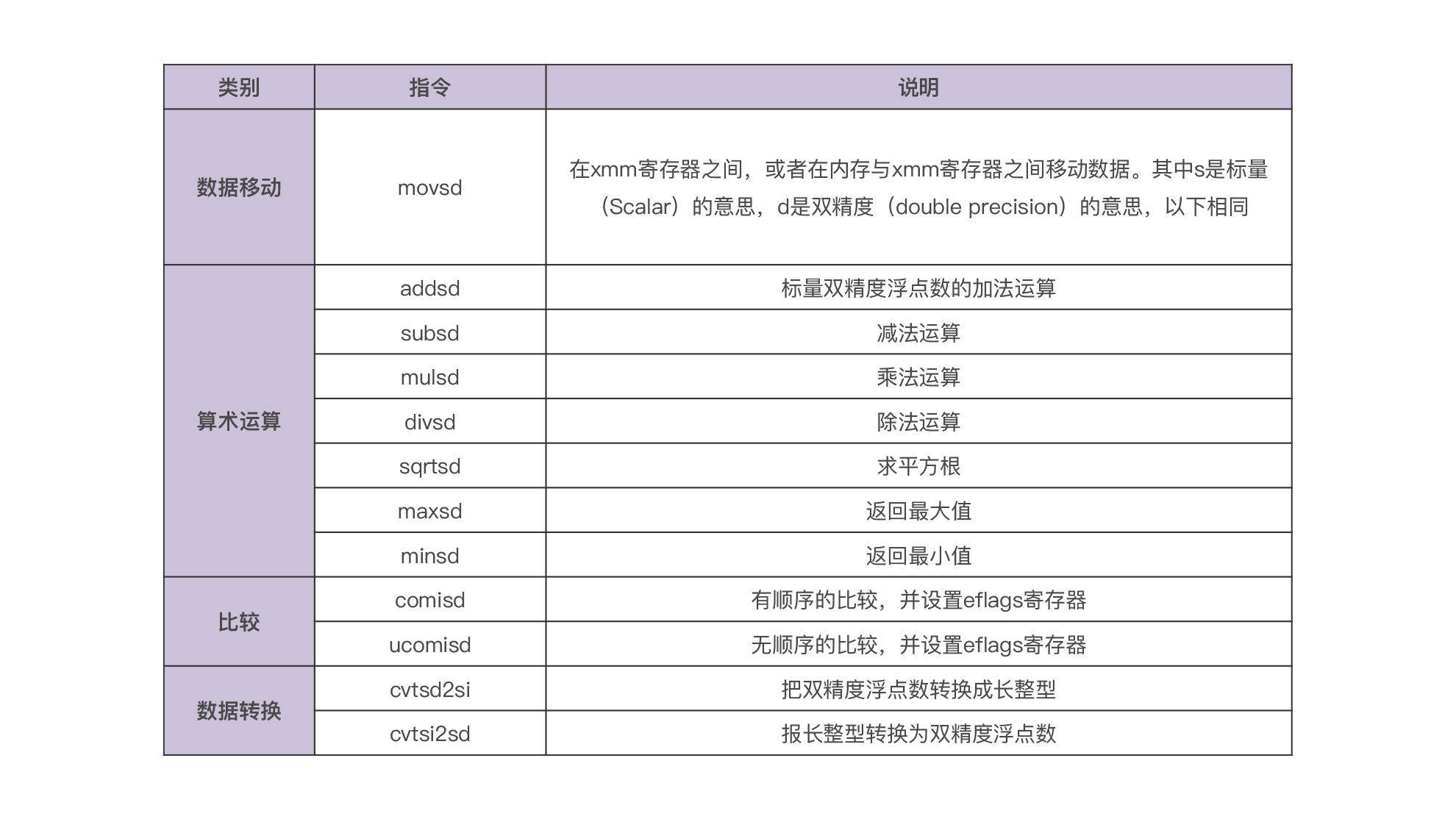
你能看到,其实这些指令数量也并不太多,很容易掌握。当然,SSE完整的指令还是不少的。SSE针对向量数据处理、整型数据处理都有单独的指令,还有一些指令是用于管理MXCSR寄存器的状态,以及对高速缓存进行管理的。如果你想了解这些,可以阅读Intel手册的第二卷:《Intel® 64 and IA-32 architectures software developer’s manual combined volumes 2A, 2B, 2C, and 2D: Instruction set reference, A- Z》
到此为止,我们初步了解了CPU硬件对浮点数计算的支持。接下来,我们还需要了解ABI方面的一些知识。
寻找ABI方面的知识,当然还是去看手册。下面的信息来自于《System V Application Binary Interface AMD64 Architecture Processor Supplement》,我也替你稍微梳理了一下重点。
首先我们要看参数传递。采用SSE指令集传递参数时,可以使用8个寄存器,从xmm0到xmm7。如果要传递的参数超过8个,也是通过栈传递。
再看看返回值。对于64位标量计算来说,我们用xmm0来传递返回值就可以了。
最后我们再看对寄存器的保护。SSE指令集用到的寄存器,都不需要跨函数调用保存。也就是说,Callee不需要保护这些寄存器中的值。
在了解了硬件对浮点数运算的支持和ABI方面的规定以后,我们就可以去动手修改我们语言中汇编代码的生成功能了。
其实,为浮点数运算和整数运算生成汇编代码的逻辑,整体上是差不多的。你只需要按照CPU架构和ABI的规定做一定的调整就可以了。这些调整主要包括:
第一,调整算法所生成的指令。
这个时候,算术运算的指令,已经从原来的addl和subl等整数运算指令,变成了addsd、subsd这些浮点数运算指令。数据移动的指令,也从原来的movl变成了movsd。其他指令也做了类似这样的调整。
第二,调整寄存器分配算法。
由于整数运算和浮点数运算使用的寄存器是不同的,所以我们可以针对两种运算分别运行寄存器分配算法来分配寄存器。
第三,调整栈桢维护逻辑。
为什么要调整这个呢?是这样,如果我们需要把双精度浮点数溢出到栈桢里保存,那它要占据8个字节。但是,原来的32位整数只需要占据4个字节呀。所以这个时候,计算维护栈桢的相关逻辑要调整了,包括计算栈桢大小,以及需要如何移动栈顶指针rsp等等都需要变动。
第四,调整函数调用逻辑。
在调用函数时,如果我们需要传递浮点数的参数,那要使用浮点数的寄存器,并且可以使用8个。超过了8个之后,是放到调用者的栈桢里。对于浮点型的返回值,也是放在浮点数寄存器xmm0里的。
但这里其实有一个隐藏的问题:如果一个函数既需要传递整型参数,又需要传递浮点型参数,那该怎么办呢?这是一个很有趣的技术点。不仅仅是传这两种参数,后面我们还需要传递字符串指针、对象指针,还有布尔值等等,其实这些在ABI手册里都有规定,你直接去查ABI手册就可以了。不过,目前我们还是先简化一下,我们规定函数的参数和返回值都必须是双精度型的,后面我们再去支持混合参数的场景。
做完这些调整以后,我们的汇编代码生成算法,基本上就能够支持浮点数运算了。具体的实现,你仍然可以去查看一下AsmGenerator和Lower的代码。
不过,除了上面这些调整以外,还有一个看似很小的技术点,但这个技术点涉及到浮点数运算的原理,所以我们有必要单独拿出来讲一讲。
编码标准这个小的技术点,涉及到我们如何在汇编代码里使用浮点型的常数,我们也叫它立即数。为什么这是一个问题呢?我们通过示例代码看一下。
我们把param_double.c代码,来编译成汇编代码看一下里面是如何使用浮点数常量的。
double foo(double p1, double p2, double p3, double p4, double p5, double p6, double p7, double p8, double p9, double p10);
double bar(){
return foo(1, 2, 3, 4, 5, 6.1, 7.2, 8.3, 9.4, 10.5);
}
param_double.c的代码很简单。里面首先有一个foo函数的签名,但并没有具体实现。然后在bar函数里传了10个参数给foo函数,这10个参数都是常数。有的参数是以整数格式提供的,但根据语言的设计,编译器会把它们强制转换为double。
然后我们用clang -S param_double.c -o param_double.s生成汇编代码。其中bar函数对应的汇编代码如下:
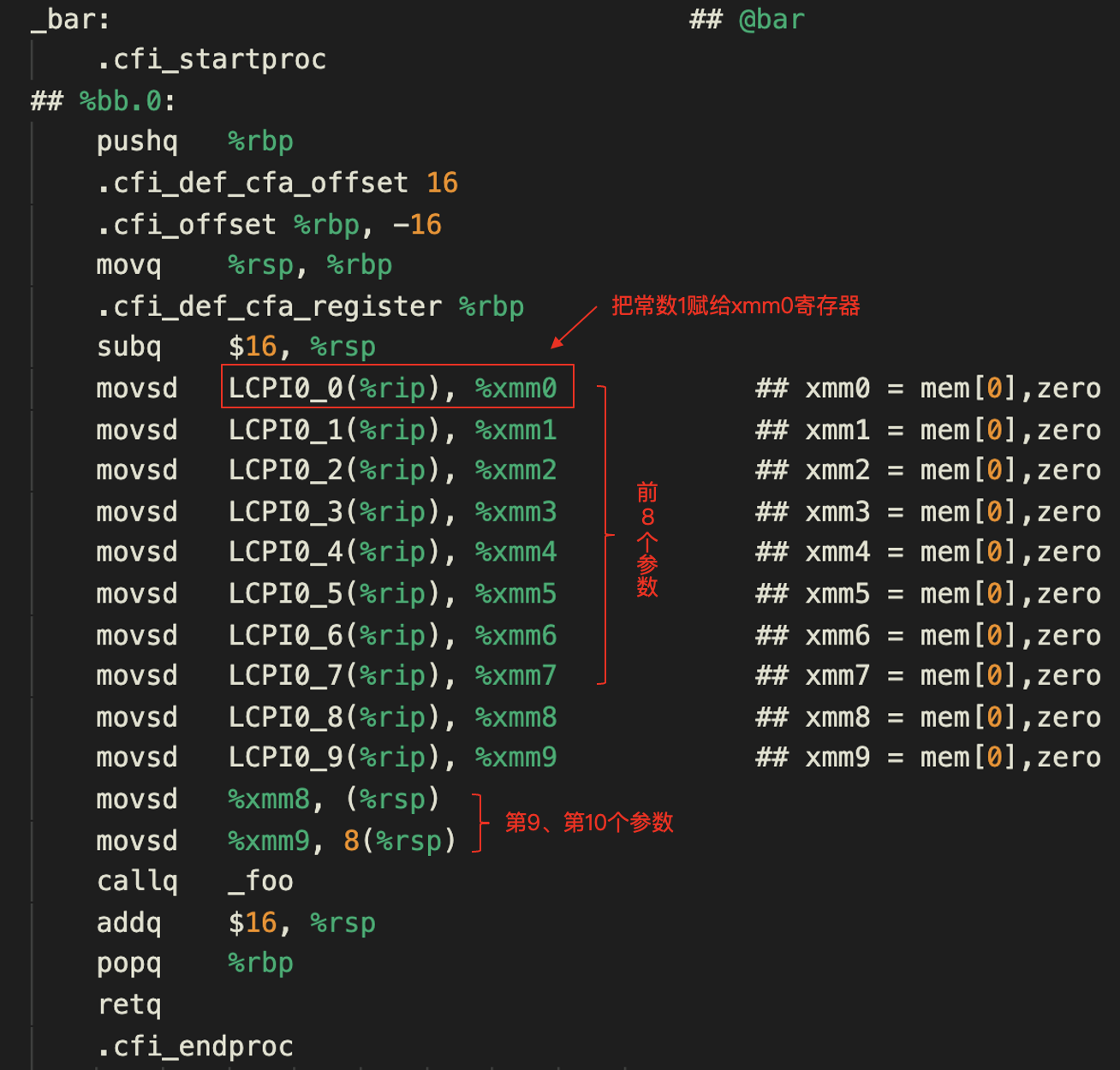
在这个汇编代码中,你会看到,在把常数赋值给寄存器的地方,用到的都是一个个的标签。比如,LCPI0_0(%rip)是第一个参数的标签,这个参数是常量1。这个标签可以被转化为一个文本段(也就是代码区)的一个地址。我们知道,%rip寄存器保存的是CPU下一条要执行的指令的地址,所以LCPI0_0(%rip)实际上记录的是常量的地址与下一条指令的地址的偏移量。通过下一条指令的地址,加上这个偏移量,就能找到常量1的存储位置。
我们再看看这个汇编代码文件的前半部分,你会看到一个文本段,用于放8字节的字面量。你可以参考下图。我在图上标注了一些必要的说明。
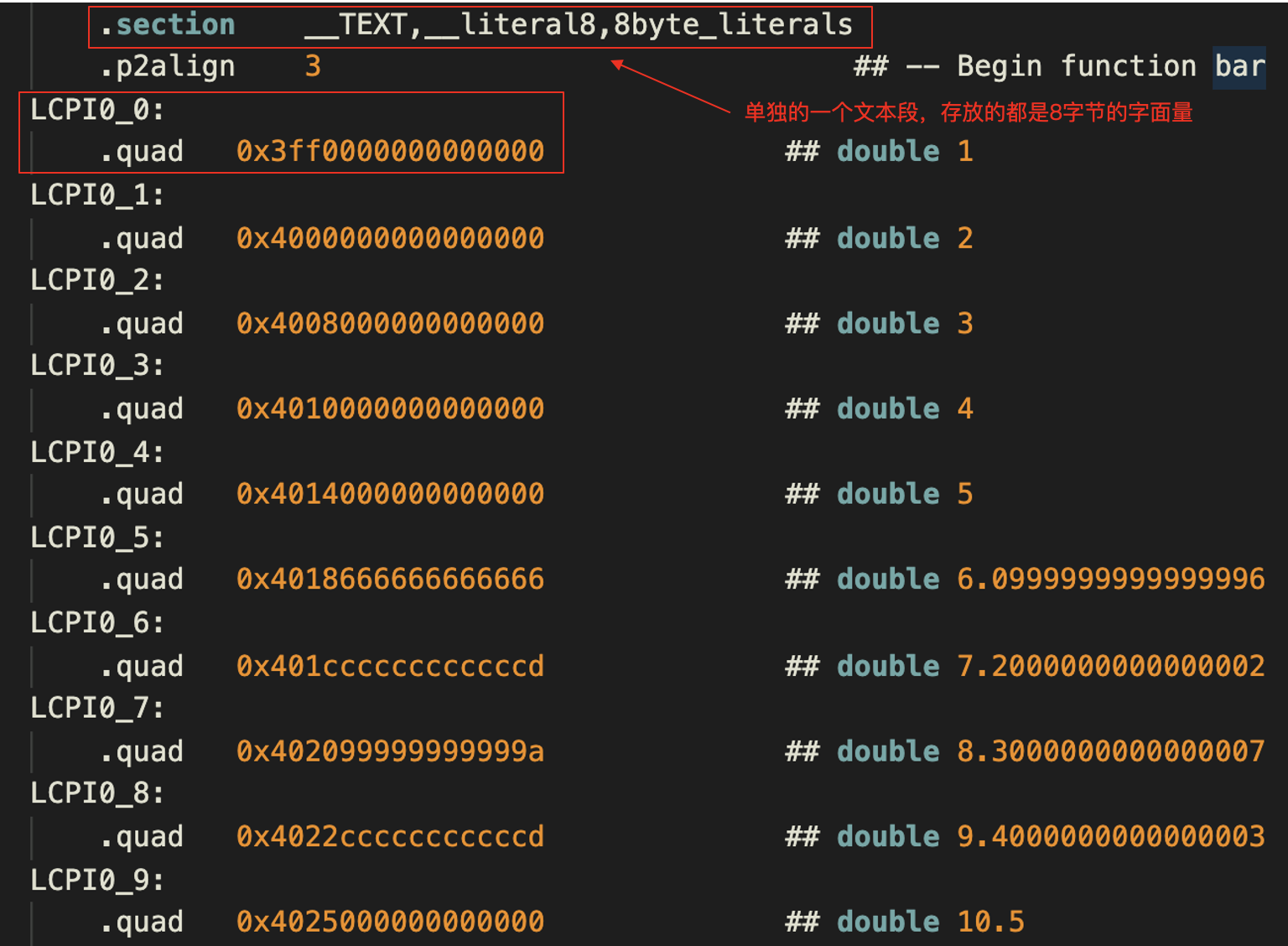
这里,.quad表示一个四个字的字面量。其中,每个字是2个字节、16位,所以加起来是8个字节、64位,正好是一个double型所需要的空间。
相信你也注意到了,在计算机里表示整数是比较简单的,基本上就是把10进制的数字转化为二进制就行了。顶多再加上一个符号位,表示正数和负数。但是要表达浮点数,就没有那么简单了。从汇编代码中你能看到,即使是1这个最简单的整数,表达成一个double型的字面量之后,也会显得很复杂。这个double值,如果我们用16进制整型格式显示,是0x3ff0000000000000。
并且,你也能看到,像1、2、3、4、5这5个整数,以及10.5这个小数,用double格式可以精确地表示出它们的数值。而对于6.1、7.2、8.3、9.4这几个小数,用double格式就只能近似地表达其值。它跟原始的值还有一点小小的误差,大约是小数点后16位的一个很小的值。这都是由浮点数的编码方式决定的。
现在问题就来了,在生成汇编代码的过程中,我们要把代码里的字面量转换成像0x3ff0000000000000(也就是1)、0x401ccccccccccccd(也就是7.2)这样的格式才可以。所以,你就必须了解浮点数的编码格式。
浮点数的编码,是在国际标准IEEE 754中规定的。对于双精度浮点数来说,它所占据64位被划分成了3段。一开头,是一个符号位,符号位是0,则表明这是个整数,如果是1,则表示负数。接下来是11位的指数位,最后是52位的有效数字位。这样加起来一共是64位。

那什么是指数位?什么是有效数字位?它们又是如何用来表示一个浮点数的呢?
原来,浮点数使用的是二进制的科学计数法来表示数字。也就是说,任何一个数字都可以表达成1.xxxxx乘以2的n次方的格式:
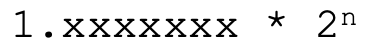
比如说,5这个数字,变成二进制格式是101,如果写成二进制的科学计数法,我们小数点前面只保留1位,就是:
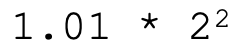
那具体编码的时候,是不是在有效数字区里存个101,在指数区存个10(也就是2)就行了呢?就像下图那样。
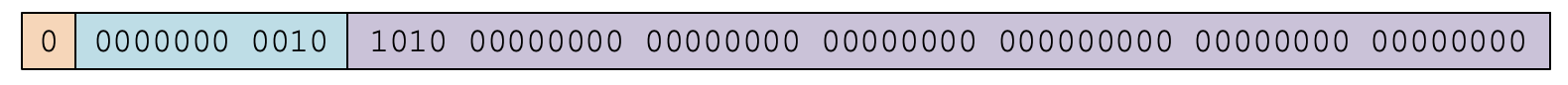
这是不行的。这里有两个地方需要调整,才能符合IEEE 754标准:
首先,我们要调整有效数字的存储。由于所有的有效数字的整数位都是1,所以我们从节约存储空间的角度看,这一位就没有必要存了。也就是说,101只存个01就行。
第二,我们要调整指数的存储。指数是可以有正有负的。比如0.05,写成二进制是0.00001100110011001100110011001100110011001100110011001101,写成科学计数法是:
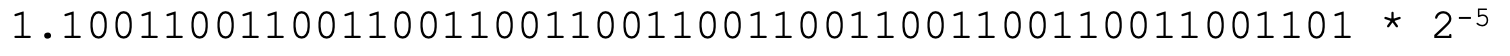
这个时候,指数位就是-5。
所以,为了能够表达指数是正数和负数的情况,IEEE754规定,要把指数加上一个常数,让所有的指数都变成正数来表达。因为2的11次方是2048,理论上指数位能够表达2048个指数值。但标准规定,当这11位都是1时,是用来表示特殊数字的:如果有效位数全为零,表示正负的无穷大(±Infinity);如果有效位不全为0,则表示NaN。
这样的话,我们就只能使用2047个指数了,其中整数1023个,负数1023个,指数0占一个。所以,我们把所有的指数都加上常数1023,就都变成正数了。而5的指数位就需要记录1023+2=1025,表达成二进制是10000000001,正好是11位,一前一后都是1,其他位是0。
好了,完成上面两个调整以后,字面量5的double格式就是:

这个数字如果表示成16进制,那就是0x4014000000000000,跟汇编代码里字面量5的数值是完全一致的。
好了,看到这里,我相信你已经掌握了双精度浮点型数字的存储方式了。掌握了原理以后,你可以自己写段代码来生成IEEE 754格式的浮点数。在课程的示例代码里,我用了一个第三方的node.js库(feross/ieee754)来把number的常数转换成用16进制的格式,就像汇编代码里的那些double常数一样。你需要用“npm install ieee754”命令来安装这个库。
好了,今天的内容就是这些。我们用了一节课的时间,讲解了支持浮点数运算的关键知识点。现在我们再来总结一下:
首先,对于每一个CPU架构来说,对浮点数运算都会有专门的支持。对于X86-64来说,我们主要使用SSE指令集进行浮点数运算。这个指令集中,标量浮点数运算的指令,跟我们前面学过的📄运算的指令,是很相似的,所以我们很容易接受。这个指令集会用到16个128位寄存器,我们做双精度浮点数的标量运算时,只会用到这些寄存器的低64位。在寄存器分配算法中,我们要针对处理浮点数和整数的指令,分别分配寄存器。
第二,我们也学习了ABI对于处理浮点数的不同规定。主要表现在参数传递和返回值上。参数传递可以使用xmm0~xmm7共8个寄存器,返回值可以使用xmm0寄存器。其他方面,比如栈桢格式方面,与之前我们学过的知识点没有什么区别。
最后,我们学习了浮点数的编码标准。根据IEEE 754标准,双精度浮点数使用1个符号位、11个指数位和52个有效数字位构成的。在这里,你最好能够了解如何手工计算出一个浮点数的存储格式,这会让你加深对这个知识点的理解。而且,我建议你不要忽略这个知识点。因为当你能对编码格式了然于胸的时候,会有助于你更顺畅地理解使用到浮点型字面量的汇编代码,也有助于你理解CPU是如何处理浮点数的。
到现在,我们的课程已经讲到了整型和双精度浮点型这两种数据类型,它们都得到了X86架构的CPU的支持。你能不能查一下,X86架构的CPU还支持哪些数据类型呢?处理这些数据类型的指令都有哪些?这些在Intel手册的第一卷都能查到。欢迎你在留言区分享你的发现。
欢迎你把这节课分享给更多感兴趣的朋友。我是宫文学,我们下节课见。
这节课涉及的代码都在asm_x86-64_d.ts中。这个代码文件是复制了asm_x86-64.ts,把它改成了支持double类型的版本。