你好,我是宫文学。
在前面两节课,我们分析了本地优化和全局优化的场景。我们发现,由于基于图IR的优点,也就是控制流和数据流之间耦合度比较低的这个特点,我们很多优化算法的实现都变得更简单了。
那么,对于过程间优化的场景,我们这个基于图IR是否也会带来类似的便利呢?
过程间优化(Inter-procedural Optimization)指的是跨越多个函数(或者叫做过程),对程序进行多方面的分析,包括过程间的控制流分析和数据流分析,从而找出可以优化的机会。
今天这节课,我们就来分析两种常用的过程间优化技术,也就是内联优化和全局的逃逸分析,让你能了解过程间优化的思路,也能明白如何基于我们的IR来实现这些优化。之后,我还会给你补充另一个优化技术方面的知识点,也就是规范化。
内联优化是最常见到的一个过程间优化场景,说的就是当一个函数调用一个子函数时,干脆把子函数的代码拷贝到调用者中,从而减少由于函数调用导致的开销。
特别是,如果调用者是在一个循环中调用子函数,那么由很多次循环累积而导致的性能开销是很大的。内联优化的优势在这时就会得到体现。
而在面向对象编程中,我们通常会写很多很简短的setter和getter方法,并且在程序里频繁调用。如果编译器能自动把这些短方法做内联优化,我们就可以放心大胆地写这些短方法,而不用担心由此导致的性能开销了。
现在我们就举一个非常简单的、可以做内联的例子看看。在这个示例中,inline函数是调用者,它调用了add函数。
//内联
function inline(x:number):number{
return add(x, x+1);
}
function add(x:number, y:number):number{
return x + y;
}
显然,在编译inline函数的时候,我们没必要额外多产生一次对add函数的调用,而是把add函数内联进来就行了,形成下面这些优化后的代码:
//内联
function inline(x:number):number{
return x + (x+1);
}
那要如何基于我们的IR实现内联优化呢?
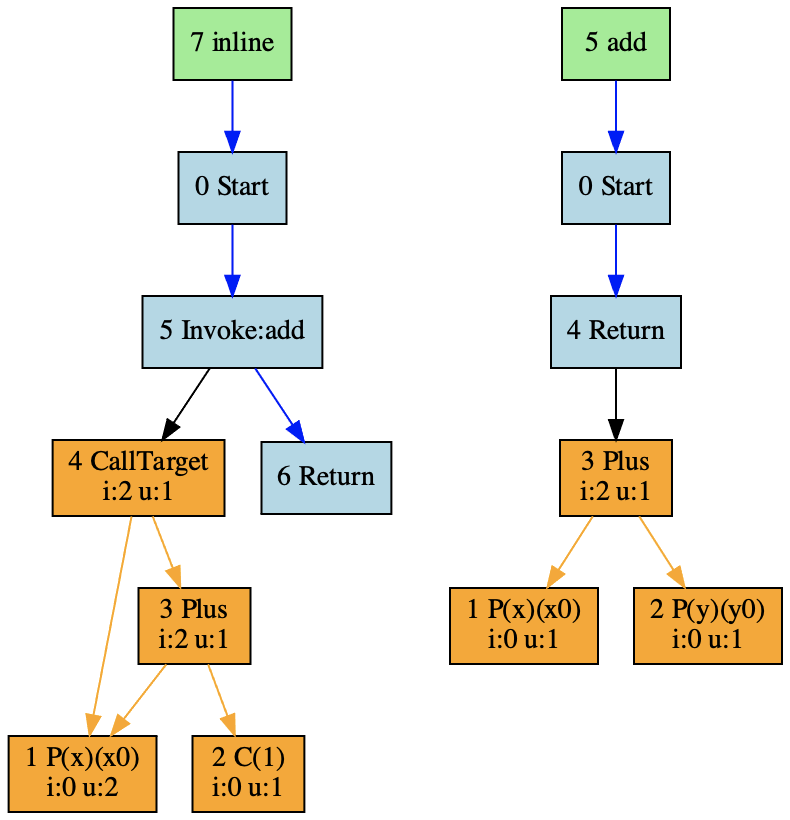
首先,我们还是看看在没有优化以前,inline和add两个函数的IR:

在inline函数的IR里,你能发现两个新的节点:一个是Invoke节点,代表函数调用的控制流;另一个是CallTarget节点,代表函数调用的数据流。
而内联优化就是要把这两个IR图合并,形成一个大的IR。如下图所示:
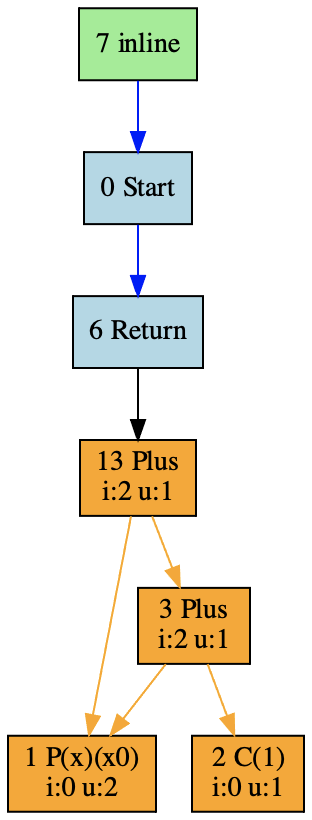
具体来说,要实现上面的合并,我们需要完成两个任务:
总的来说,整个算法都是去做节点的替换和重新连接,思路还是很清晰的。
我们之前说过,编译器在做了一种优化以后,经常可以给其他优化制造机会。在这里,内联优化不仅仅减少了函数调用导致的开销,它还会导致一些其他优化。比如说,我们在Inline函数里调用add函数的时候,传入两个参数x和-x,如下面的示例代码:
//内联
function inline2(x:number):number{
return add(x, -x);
}
function add(x:number, y:number):number{
return x + y;
}
那么内联之后,这里就相当于计算x+(-x)的值,那也能计算出一个常量0。至于如何把x+(-x)化简成0,我先留个悬念,你先自己思考一下,我们这节课后面会介绍到。
//内联
function inline(x:number):number{
return x + (-x); //常量0
}
再比如,我们在主函数里调用add的时候,传的参数是常量。那么内联以后,我们就可以进行常量传播和常量折叠的优化,在编译期就能计算出结果为5:
//内联
function inline2(x:number):number{
return add(2, 3);
}
function add(x:number, y:number):number{
return x + y;
}
当然了,内联优化是最常见的一种过程间优化。除了内联优化之外,过程间的逃逸分析也值得拿出来单独说一下。
对于像Java这样的面向对象语言来说,逃逸分析是经常被采用的技术。我在《编译原理实战课》的第15节,曾经专门讨论了Java JIT编译器中的逃逸分析技术。
简单来说,逃逸分析的目的,是分析一个对象的生命期有没有超过函数的生存期,从而进行一些优化。比如下面这段代码中,我们声明了一个Rectangle类,它有width和height的属性,并且有一个方法能够计算面积。然后在一个foo函数中,我们创建了一个Rectangle对象,并且为了调用它的area方法,计算出面积。
class Rectangle{
width:number;
height:number;
constructor(width:number, height:number){
this.width=width;
this.height = height;
}
area():number{
return this.width*this.height;
}
}
function foo(width:number, height:number){
let rect = new Rectangle(width, height);
return rect.area();
}
分析foo的代码,你会发现rect的生存期始终在foo函数之内。这个时候,我们说rect对象没有逃逸。当foo函数返回时,这个对象也就没有用了。因为这个特点,所以我们可以做三个方面的优化:
第一个优化是栈上内存分配。通常,我们是在堆里为对象申请内存的,然后在某个时机用垃圾回收程序来回收。但rect对象的生存期小于foo函数的生存期,也就是说,在foo函数返回以后,也不会有其他的程序来访问这个对象,所以这个对象所需要的内存,直接在栈上申请就行了。这样,当函数退出的时候,rect对象的内存也就直接被回收,不需要通过GC回收了,内存管理的性能就更高了。
第二个优化是标量替换。也就是把对象的属性拆散,变成width和height两个本地变量。这样,它们就可以被放到寄存器里,而不是非要通过内存来访问,从而提高了性能。
第三个优化是锁消除或者同步消除。在编写并发程序的时候,我们需要用锁来做线程的同步,从而避免多个线程同时访问某个对象而引起数据的混乱。而且,因为rect对象没有逃逸出函数体,也就是说它注定只能被一个线程访问,所以我们对rect对象的访问也就不需要做线程间的同步,这也就消除了由于同步而引起的性能开销。
好,上面就是对逃逸分析的概要介绍。逃逸分析可以基于单个函数或方法,也可以跨域多个函数来分析,从而做出优化。
比如,基于上面的例子,我又写了两个新的函数。其中函数biggerThan,能够接受两个Rectangle对象,并比较它们面积的大小。在bar函数里,我创建了两个Rectangle对象,并调用了biggerThan函数。
function bar(w1, h1, w2, h2):booelan{
let rect1 = new Rectangle(w1, h1);
let rect2 = new Rectangle(w2, h2);
return biggerThan(rect1, rect2);
}
function biggerThan(rect1:Rectangle, rect2:Rectangle):boolean{
return rect1.area()>rect2.area;
}
你用肉眼就可以看出,虽然rect1和rect2从bar函数传递了出去,传给了biggerThan函数,但它们并没有继续从biggerThan函数往外逃逸。所以,如果我们把这两个函数看做一个整体,那么rect1和rect2对象仍然是没有逃逸的。
所以呢,你仍然可以运用这个分析结果,来实现一些优化,比如说实现栈上内存分配和同步消除的优化。
那了解了逃逸分析的作用以后,我们如何基于当前的IR来实现逃逸分析呢?
经典的逃逸分析采用一种叫做连接图(Connection Graph)的算法。简单地说,就是分析出程序中对象之间的引用关系。整个分析算法是建立在这样一种直觉认知上的:基于一个连接图,也就是对象之间的引用关系图,如果 A 引用了 B,而 A 逃逸了,那么也就意味着B逃逸了。也就是说,逃逸是有传染性的。
而基于当前的IR,我们可以很方便地得到上面说的的连接图,有利于我们分析对象逃逸的情况。当然,单个的对象是很容易分析的。不过,即使是多个对象之间存在关联,也能够在数据流中体现出来。我们可以看下这个例子:
let person = new Person();
person.name = "Richard";
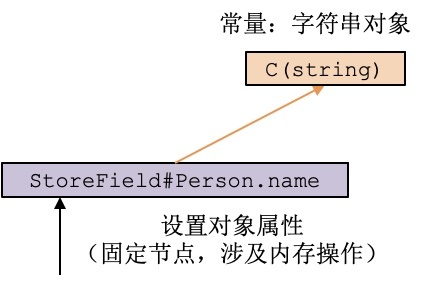
在这里,我们给person的name属性做了赋值。这样,person对象就跟一个string对象建立了关联。如果person对象逃逸到了函数或方法之外,那么该string对象也跟随着逃逸。反之,那么这两个对象都没有逃逸,那都可以在栈上申请内存。
表达上面两个对象之间关系的IR如下图。基于这个IR,我们就能得到对象之间的关联了:
好了,到目前为止,我们已经分析了基于IR在本地、全局和过程间做优化的一些场景。在实际的编译器中,我们还会实现很多的场景,比如把循环拉直,调整内循环和外循环,把用不到的分支去掉等等。但这些优化的本质,都是基于控制流和数据流的分析对IR图进行修改。你把握住这个关键点就行了。
最后,我再讲一个Java的JIT编译器Graal中经常见到的一种优化方法,作为这三节课的结尾,这个优化方法就是规范化。
在《编译原理实践课》中,我曾经对Graal编译器做过剖析。如果你跟踪Graal的编译过程,你会发现它的编译过程中会涉及100多个pass,也就是用各种算法对一个IR图处理了一百多遍。其中很多pass都是我们已经讲过的,比如死代码删除、逃逸分析,等等。但还有一个使用频率很高的优化方法,叫做Canonicalizer,也就是规范化。
那什么是规范化呢?规范化就是针对各种计算节点所做的化简操作。比如,对于减法运算,如果减法两边的Node是同一个节点,那我们就可以计算出常量0来:
let y = x - x; //规范化结果为0。
而对于加法运算,如果两个其中一个节点是另一个节点取负值,那也可以化简,结果为0。
let y = x + (-x); //规范化结果为0。
其他类似的规范化操作还包括:
刚才列出的这些,都属于加法和减法运算。类似的是,对于其他运算,我们也都可以进行化简或者变形。比如,对于a2或a4,规范化后会变成移位运算。
你也可以想象出来,上述规范化的操作,基于我们现在的IR,实现起来都不是很复杂,我们仍然只要对图中的节点进行模式的匹配和修改就行了。
总的来说,上述化简操作,属于算术化简和符号运算的范畴。比如,把1+ 2化简成3,这属于算术化简,基于算术运算的规则就行。而把(a - b) + b化简成a,这就属于符号运算的范畴,也就是说,运算的对象不再是具体的数字,而是像代数里的一个个变量。
符号运算是从编译原理衍生出来的一项技术。一些数学软件包,具备基于符号进行运算的能力。比如,你输入一个复杂的公式,它能够把它化简成一个简单的公式。或者你输入一个命题,它能给你推理,并证明该命题是真还是假。
我自己特别关注的是对关系运算和逻辑运算的化简,比如(!a || !b)会被化简成!(a&&b),a || false会被化简成a,a || true会被化简成ture,等等。我对它们比较关注的原因,是想把它们借鉴进类型运算中。比如,变量a的类型声明为string|null,如果再加上一个条件if(a),那么if块中,a的类型就会被窄化成string:
let a: string|null;
//some code
if(a){
//现在a的类型肯定是string。
}
之前我们也学习了类型窄化,目前,在我们这门课中实现的类型窄化的算法,都是采用集合运算的规则进行处理的。如果我们在这里面加入符号运算,那么我们再进行类型窄化就会变得更简单。我会在开源版本的PlayScript中再进行算法的迭代,你感兴趣的话可以继续关注。
这节课的内容就是这些了。在这节课里,我通过内联优化和过程间的逃逸分析,让你建立对过程间优化的直观认识。对于这节课的重点,我们再重新回顾一下:
首先,内联优化的实质是把两个函数的IR拼接在一起,把形参节点替换成实参节点。内联优化通常还会为其他优化创造出机会。
第二,逃逸分析的作用在于,一旦我们确定出某个对象并没有逃逸,那么就可以实现栈上内存分配、标量替换和同步消除的优化。通过跨越多个函数进行分析,我们可以发现出更多的对象是没有逃逸的,从而可以做更多优化。逃逸分析也可以基于IR图来进行。
最后,除了过程间优化,我在这节课还补充了一个规范化方面的知识点。规范化主要是针对各种运算节点,实现符号化简和代数化简。其中的符号运算方面的技术,值得我们关注,它会帮助我们更好地进行类型的处理。
关于基于IR做中端优化,我们就介绍这些。下一节课,我们将介绍如何把这些IR做Lower处理,并最终生成汇编代码。在这个过程中,我们仍然需要用到一些优化技术。
在讲解中端优化的内容中,我们发现,受益于基于图的IR的优点,实现很多优化算法都变得更简单了。但是,事物往往是平衡的,有一方面的优点,往往就会带来另一方面的缺点。那么你能不能分析一下,这种基于图的IR,会让哪些操作反而变得更复杂呢?
欢迎你基于对图这种数据结构的认识来发表一下观点。这种分析,会让你从更高的高度来审视对数据结构设计的取舍。
欢迎你把这节课分享给更多感兴趣的朋友。我是宫文学,我们下节课见。