不管你有没有剁过手,你对“看了这个商品的还看了”这样的推荐形式一定不陌生。无论是猫还是狗,或者是其他电商网站,这样的推荐产品可以说是推荐系统的标配了。
类似的还有,如点评标记类网站的“喜欢了这部电影的还喜欢了”,社交媒体网站的“关注了这个人还关注了”,这些都只是文案类似,动词不同而已。
这样的推荐形式背后都是来自一个古老的推荐算法,叫做基于物品的协同过滤,通常也被叫作Item-Based,因为后者更容易搜索到相关的文章,所以被更多地提及。
如果做推荐系统不知道“基于物品的协同过滤”,那等同于做程序员不懂得冒泡排序。这个朴素的算法,就像是乔峰大战聚贤庄所用的“太祖长拳”一样,简单直接有效,读过高中就懂,用得好也能够战倒绝大多数的武林豪杰。今天,我就来和你聊聊这个朴素的算法。
基于物品的协同过滤算法诞生于1998年,是由亚马逊首先提出的,并在2001年由其发明者发表了相应的论文( Item-Based Collaborative Filtering Recommendation Algorithms )。
这篇论文在Google学术上引用数已近7000,并且在WWW2016大会上被授予了“时间检验奖”,颁奖词是:“这篇杰出的论文深深地影响了实际应用”。历经了15年后仍然在发光发热,这个奖它显然受之无愧。
虽然今天各家公司都在使用这个算法,好像它是一个公共资源一样,然而并不是这样,亚马逊早在1998年,也就是论文发表的三年前就申请了专利。
讲完了算法的八卦,开始说正事了。
在基于物品的协同过滤出现之前,信息过滤系统最常使用的是基于用户的协同过滤。基于用户的协同过滤首先计算相似用户,然后再根据相似用户的喜好推荐物品,这个算法有这么几个问题:
和基于用户的不同,基于物品的协同过滤首先计算相似物品,然后再根据用户消费过、或者正在消费的物品为其推荐相似的,基于物品的算法怎么就解决了上面这些问题呢?
首先,物品的数量,或者严格的说,可以推荐的物品数量往往少于用户数量;所以一般计算物品之间的相似度就不会成为瓶颈。
其次,物品之间的相似度比较静态,它们变化的速度没有用户的口味变化快;所以完全解耦了用户兴趣迁移这个问题。
最后,物品对应的消费者数量较大,对于计算物品之间的相似度稀疏度是好过计算用户之间相似度的。
根据我在上一篇文章中所说,协同过滤最最依赖的是用户物品的关系矩阵,基于物品的协同过滤算法也不能例外,它的基本步骤是这样的:
前面较为笼统地说要计算物品之间的相似度,现在详细说说这块。从用户物品关系矩阵中得到的物品向量长什么样子呢?我来给你描述一下:
接下来就是如何两两计算物品的相似度了,一般选择余弦相似度,当然还有其他的相似度计算法方法也可以。计算公式如下:
$$sim(i,j) = \frac{\sum_{k=1}^{n}{R_{ik} * R_{jk}}} { \sqrt{\sum_{k=1}^{n}{R_{ik}^{2}}} \sqrt{\sum_{k=1}^{n}{R_{jk}^{2}}}}$$
用文字解释一下这个公式:
分母是计算两个物品向量的长度,求元素值的平方和再开方。分子是两个向量的点积,相同位置的元素值相乘再求和。
很简单,因为这个公式出自中学数学课本,所以我刚才说读过高中就懂。
这个公式的物理意义就是计算两个向量的夹角余弦值,相似度为1时,对应角度是0,好比时如胶似漆,相似度为0时,对应角度为90度,毫不相干,互为路人甲。
看上去计算量很大,貌似每一个求和的复杂度都是和向量维度、也就是用户数量一样的。但是别忘了,前面我说过他们都是稀疏向量,也就是向量中绝大多数值都是0,求和时不用算,点积时更不用算,甚至求点积时只用管两个物品的公共用户,只是少许几个乘积而已。
物品之间的相似度计算是这个算法最可以改进的地方。通常的改进方向有下面两种。
1. 物品中心化。把矩阵中的分数,减去的是物品分数的均值;先计算每一个物品收到评分的均值,然后再把物品向量中的分数减去对应物品的均值。这样做的目的是什么呢?去掉物品中铁杆粉丝群体的非理性因素,例如一个流量明星的电影,其脑残粉可能会集体去打高分,那么用物品的均值来中心化就有一定的抑制作用。
2. 用户中心化。把矩阵中的分数,减去对应用户分数的均值;先计算每一个用户的评分均值,然后把他打过的所有分数都减去这个均值。
这样做的目的又是什么呢?每个人标准不一样,有的标准严苛,有的宽松,所以减去用户的均值可以在一定程度上仅仅保留了偏好,去掉了主观成分。
上面提到的相似度计算方法,不只是适用于评分类矩阵,也适用于行为矩阵。所谓行为矩阵,即矩阵元素为0或者1的布尔值,也就是在前面的专栏中讲过的隐式反馈。隐式反馈取值特殊,有一些基于物品的改进推荐算法无法应用,比如著名的Slope One算法。
在得到物品相似度之后,接下来就是为用户推荐他可能会感兴趣的物品了,基于物品的协同过滤,有两种应用场景。
第一种属于TopK推荐,形式上也常常属于类似“猜你喜欢”这样的。
出发方式是当用户访问首页时,汇总和“用户已经消费过的物品相似”的物品,按照汇总后分数从高到低推出。汇总的公式是这样的:
$$\hat{R_{ui}} = \frac{\sum_{j=1}^{m}{sim(i,j)* R_{uj}}}{\sum_{j=1}^{m}{sim(i,j)}}$$
这个公式描述一下,核心思想就和基于用户的推荐算法一样,用相似度加权汇总。
要预测一个用户u对一个物品i的分数,遍历用户u评分过的所有物品,假如一共有m个,每一个物品和待计算物品i的相似度乘以用户的评分,这样加权求和后,除以所有这些相似度总和,就得到了一个加权平均评分,作为用户u对物品i的分数预测。
和基于物品的推荐一样,我们在计算时不必对所有物品都计算一边,只需要按照用户评分过的物品,逐一取出和它们相似的物品出来就可以了。
这个过程都是离线完成后,去掉那些用户已经消费过的,保留分数最高的k个结果存储。当用户访问首页时,直接查询出来即可。
第二种属于相关推荐,也就是我们今天专栏题目所指的场景。
这类推荐不需要提前合并计算,当用户访问一个物品的详情页面时,或者完成一个物品消费的结果面,直接获取这个物品的相似物品推荐,就是“看了又看”或者“买了又买”的推荐结果了。
经典的基于物品推荐,相似度矩阵计算无法实时更新,整个过程都是离线计算的,而且还有另一个问题,相似度计算时没有考虑相似度的置信问题。例如,两个物品,他们都被同一个用户喜欢了,且只被这一个用户喜欢了,那么余弦相似度计算的结果是1,这个1在最后汇总计算推荐分数时,对结果的影响却最大。
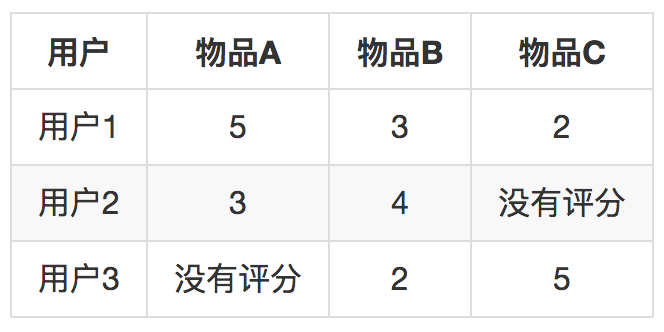
Slope One算法针对这些问题有很好的改进。在2005年首次问世,Slope One算法专门针对评分矩阵,不适用于行为矩阵。Slope One算法计算的不是物品之间的相似度,而是计算的物品之间的距离,相似度的反面。举个例子就一目了然,下面是一个简单的评分矩阵:

这个矩阵反应了这些事实:用户1给物品A、B、C都评分了,分别是5,3,2;用户2给物品A、B评分了,分别是3、4;用户3给物品B、C评分了,分别是2、5。现在首先来两两计算物品之间的差距:
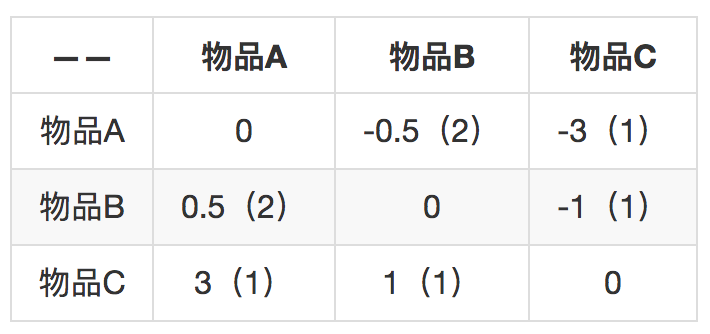
括号里表示两个物品的共同用户数量,代表两个物品差距的置信程度。比如物品A和物品B之间的差距是0.5,共同用户数是2,反之,物品B和物品A的差距是-0.5,共同用户数还是2。知道这个差距后,就可以用一个物品去预测另一个物品的评分。
如果只知道用户3给物品B的评分是2,那么预测用户3给物品A的评分呢就是2.5,因为从物品B到物品A的差距是0.5。
在此基础上继续推进,如果知道用户给多个物品评分了,怎么汇总这些分数呢?
方法是把单个预测的分数按照共同用户数加权求平均。比如现在知道用户3不但给物品B评分为2,还给物品C评分为5,物品B对物品A的预测是2.5分,刚才计算过了,物品C给物品A的预测是8分,再加权平均。
$$ \frac{8*1 + 2.5 * 2 }{(1+2)} = 4.33 $$
就得到了推荐分数为4.33分。是不是很简单?
今天我们在基于用户的协同过滤基础上介绍了比较常见的一个算法:基于物品的协同过滤。这个方法常常在电商网站上见到,“买了又买”“看了又看”这样的相关推荐,都是由这个推荐算法产生。
最后我们介绍了一个改良版的基于物品推荐算法Slope One。这里也留下了一个问题给你:为什么说Slope One可以做到在线更新呢?欢迎留言讨论。

评论