
你好,我是建元。
前面几节课,我们讲了实时音频前处理中的降噪算法。从这节课开始,我们将会看看语音交互或者说音频通信领域的另一项不可或缺的技术:声学回声消除(Acoustic Echo Cancellation, 简称AEC)。
回声消除算法在实时音频互动链路中和很多其它模块以及硬件都会有耦合。这节课我们主要看看实时音频互动链路中回声是如何产生的以及回声消除算法的基本原理。
需要注意的是,这节课涉及到的公式比较多。不过不用担心,只要你理解了原理,就很容易能明白公式的含义,从而能够记住公式的定义。
回声是如何产生的呢?我们可以通过下面的图来看一下,这是一个出现回声的经典场景。

图1中B端的人在说话,说话的声音会被B端的麦克风采集。麦克风采集到的语音信号转为数字信号后经过网络传输到A端,在A端的扬声器会把收到的语音信号转成声波播放出来,同时A端的麦克风又会把扬声器的声音采集回来,通过网络又传回给了B端。这时B端的人就会听到自己发出去的声音,我们把这个声音就叫做回声。
在音频实时互动的场景里,回声会严重影响通话体验,自己的声音不断被打断,而且对端的声音可能会和回声混在一起,这样会显著降低语音的可懂度。那么相对地,AEC的任务就是为了消除这个回声。在AB端互通的时候,我们需要使用AEC,在A端把麦克风采集到的信号中和B端相关的声音去掉,只保留A端的音源的声音发给B端。
那么是不是把A端麦克风采集到的信号减去A端扬声器中的信号就能把回声消除了呢?我们先来看看A端的回声消除的基本原理,再回过头来解答这个问题。
在近端接收到的远端的声音信号我们把它叫做参考信号$x(n)$。在经过扬声器播放、空气传播、房间墙体反射、麦克风采集后,参考信号不可避免地会产生很多变化。我们把这个变化用数学的方式来表达就叫做回声路径的传递函数,一般记作$f$。那么近端麦克风采集的回声信号$echo(n)$可以用公式1来表示:
$$echo(n)=f(x(n)) \text{ 公式1}$$
近端除了回声信号还有近端自己的声音,比如近端人说话的声音。那么近端麦克风收到的信号$z(n)$其实是近端声音$y(n)$和回声信号之和,如公式2所示:
$$z(n)=echo(n)+y(n)\text{ 公式2}$$
而回声消除算法的目的就是通过算法估计出回声路径的传递函数$f$,我们把算法估计出的传递函数定义为$f’$,那么经过回声消除后得到的近端信号$z’(n)$为公式3所示:
$$z’(n)=z(n)-f’(x(n))\text{ 公式3}$$
将公式1和公式2代入公式3,我们可以得到公式4:
$$z’(n)=f(x(n))-f’(x(n))+y(n)\text{ 公式4}$$
我们看到如果估计的传递函数$f’$和真实的传递函数$f$是一致的,那么回声就被完美消除了。但在真实的场景中传递函数的估计是一件比较困难的事情。
这是因为AEC算法需要面对复杂的、时变的声学环境。比如,扬声器和麦克风的播放失真、采集失真会给声学信号带来很多非线性的变化,并且设备、系统调度的不稳定可能造成回声和远端接收信号的延迟抖动。同时诸如房间的混响、设备所处位置的变化,都会带来回声路径的变化。
因此,AEC算法必须能够快速地自适应地去估算出这些回声路径的变化。如果估计不准,就会导致回声泄漏或者近端声音被压制,甚至造成丢字、卡顿等现象,从而严重影响实时音频互动的质量。所以回到之前的问题,我们知道回声消除是做减法,但又不是直接相减就能解决。
那么我们是如何让算法自动快速地进行回声消除呢?AEC技术经过半个多世纪的发展,在不断的实践中已经摸索出一套以自适应滤波为基础的回声消除方法。自适应滤波的核心思想就是用实时更新的滤波器的系数来模拟真实场景的回声路径,然后结合远端信号来估计出回声信号,再从近端采集的混合信号中减去估计的回声,从而达到消除回声的目的。
接下来我们就先来看看自适应滤波的基本原理。
在一个相对稳定的声学环境中,回声路径中的延迟和房间的混响、音量大小的变化其实都可以看作是对远端信号做了一系列的线性变化。这种线性变化我们可以用一个线性离散的FIR线性滤波器来表示,公式1就变成了公式5:
$$echo’(n)=\sum_{k=0}^{\infty}{w_{k}}x(n-k),n=1,2,3,…\text{ 公式5}$$
其中$w_{k}$代表第$k$个滤波器系数。如果在近端除了回声信号没有别的声音的时候,那么其实接收到的信号就是回声信号,即$z(n)=echo(n)$。这种情况我们一般叫做“单讲”。在这种情况下,我们的回声估计误差$e(n)$可用公式6表示:
$$e(n)=echo(n)-echo’(n)\text{ 公式6}$$
你还记得之前降噪讲到过的降噪算法第三招中的维纳滤波么?其实维纳滤波就是以估计误差e(n)的最小平方作为最优解的线性滤波器。也就是通过计算最小均方差(Mean Square Error,简称MSE)来求取滤波器系数$\mathbf{W}$($w_{k}\in \mathbf{W}$)。公式7为求解最小MSE的代价函数。
$$\mathbf{J}=\mathbf{E}[e^{2}(n)]\text{ 公式7}$$
我们知道想要让函数值最小,其实就是让函数的全微分等于0。其求解过程可以用维纳-霍夫方程来表示:
$$\mathbf{W}=\mathbf{R}^{-1}\mathbf{P}\text{ 公式8}$$
其中,$\mathbf R$是参考信号$x(n)$序列的相关矩阵,$\mathbf{P}$是参考信号和回声信号$echo(n)$的互相关矢量。这样滤波器的系数似乎就可以得到了。但是你试想一下,假设音频的采样率是48kHz,如果只取1秒的信号来求解,那么$\mathbf R$矩阵的维度就是48000乘以48000。
显然要实时求一个这么大的矩阵的逆矩阵,算力是不可能支持实时计算的。我们把这种直接求得的解叫做维纳解,虽然它是最准确的,但是计算量过于庞大,而且当回声路径变化的时候我们需要重新计算维纳解。所以很显然维纳解并不适合在实时音频互动中使用。
那么有什么办法能实时求解滤波器系数呢?其实自适应滤波器的核心思想是在面对回声路径不断变化的场景,比如移动电话等时,我们可以使用梯度下降法来迭代的计算滤波器系数。
在计算代价函数的时候我们让$\mathbf{W}$系数朝着梯度相反的方向或者说朝着减少代价函数的方向移动。随着迭代次数的增加,$\mathbf{W}$会逐渐的向维纳解收敛。这样当回声路径发生变化的时候,$\mathbf{W}$就会重新收敛,从而我们就可以实时的追踪回声路径的变化了。
那么这个迭代计算具体是怎么实现的呢?下面我们就通过两个算法来看一下迭代计算的过程。
最小均方算法LMS(Least Mean Square)是最早提出,也是最基础的自适应滤波方法。它的基本原理可以表示为公式9:
$$\mathbf{W}(n+1)=\mathbf{W}(n)+\mu \mathbf{X}(n)\mathbf{e}(n)\text{ 公式9}$$
其中,$\mathbf{W}(n)$代表第n次迭代时的滤波器的系数向量,$\mathbf{X}(n)$是第n次迭代的输入向量,$\mathbf{e}(n)$是第n次迭代的误差,$\mu$是步长因子。我们可以看到步长因子$\mu$决定了滤波器系数的收敛速度,且$\mu$越大收敛越快。
最小均方算法的梯度下降是随机的,随着迭代次数的增加它会不断逼近维纳解。但是我们看到公式9里梯度下降也会受到输入向量$\mathbf{X}(n)$大小的影响。也就是说,如果远端信号音量比较小,那这时系数向量的收敛速度会变得很慢;反过来,$\mathbf{X}(n)$很大的时候会导致梯度放大,从而系数向量的收敛变快。
那么怎么解决这个音量变化带来的收敛波动问题呢?
其实我们可以通过$\mathbf{X}(n)$的大小来动态调节步长因子,这样就可以把$\mathbf{X}(n)$进行归一化。这就是NLMS算法的由来。NLMS算法的迭代步骤如公式10、11所示:
$$\mathbf{W}(n+1)=\mathbf{W}(n)+\mu(n) \mathbf{X}(n)\mathbf{e}(n)\text{ 公式10}$$
$$\mu(n)=\frac{\tilde{\mu}}{||\mathbf{X}(n)||^2+\delta}\text{ 公式11}$$
其中,$\tilde{\mu}$是一个常量,取值范围在0~2,$\delta$为一个大于0的常数,主要是为了防止$\mathbf{X}(n)$过小导致的梯度爆炸。NLMS相对于LMS通过归一化的方式提升了算法的收敛速度。目前NLMS算法已经成为AEC算法中最常用的算法之一。
那么只有NLMS是不是就足够了呢?其实这里面还有三个很重要的问题没有解决。下面我就来简单介绍一下这三个问题。
第一个问题是回声延迟。公式9~11中$\mathbf{X}(n)$是一段有限长度的输入信号,这个长度也就是我们常说的滤波器的感知长度。如果实际回声信号的传递路径很长,比如有很大的延迟和混响,那么我们就需要用一个很长的$\mathbf{X}(n)$作为输入才能估计出回声信号的传递函数。然而一个感知长度很大的滤波器需要的算力也会随之增加,这样就会对AEC的实时性造成挑战。
为了解决这个问题,最先想到的就是把延迟进行单独计算。我们可以看到假设回声信号的延迟为$dn$,那么在公式5里延迟的表示就是$w_{k}=0\text{,}k\in[0,dn-1]$。如果我们能够把延迟估计出来,那么权重为0的系数就不需要放到NLMS里去估计了,那么整体的算力就可以降下来。同时有了延迟估计,NLMS只需要估计后面非0部分的权重,从而收敛速度也可以变快。
延迟估计的方法也比较简单,其实就是移动远端信号的起始位置,然后和回声信号计算互相关性,并找到互相关最大的位置。这个位置就是我们要的延迟。
第二个问题是双讲。前面讲维纳滤波的时候讲到了“单讲”。所谓“双讲”,就是远端和近端同时说话或者说两侧都有明显的声音。那在这个时候麦克风采集的信号除了回声还有混入了近端的声音。又NLMS是依赖于回声信号来进行估计的,而这时如果用麦克风采集的信号作为回声信号,就会导致滤波器无法收敛到正确的位置,从而产生回声泄漏或近端声音被损伤。
因此,我们一般会利用远端和近端信号先做一个简单的判断,此时是单讲还是双讲状态。如果是单讲,那么滤波器系数照常迭代更新;如果是双讲,则需要通过调节步长因子等方法停止或者减缓滤波器的更新。双讲检测的方法主要是结合能量和远、近端信号的相干性来做一个判断。如果远端和近端能量都比较高但是相干性却不强,那么就说明远端和近端都有声音,也就是双讲的状态。
这里你可以思考一下,我们在现实生活中可能经常会碰到的一个现象:如果和对方打网络电话的时候,我们从一个房间走到另一个房间,比如从会议室走到走廊,对面反馈说听到了回声。
这其实就和AEC的双讲时的策略有关,如果你和对端同时说话恰巧在此刻你换了个地方,也就是回声路径发生了改变。但由于是双讲的状态,滤波器没有及时更新,这时候就会漏回声。所以双讲检测可以防止滤波器发散。但这其实也并不是一个完美的解决方案,可能还会导致回声泄漏。只是这种双讲时,恰巧换房间的情况不是那么常见,所以双讲检测依然是回声策略中常见的调整依据。
第三个问题是我们看到NLMS等算法中实际上估计的是一个线性的滤波器。但是我们之前有讲到扬声器、麦克风等都可能会导致一些非线性的变换。那么这时线性滤波器可能就无法处理了。一般来说一些廉价或者说声学特性比较差的设备导致的非线性失真比较多,所以出现回声的概率也更大。
在实时音频互动刚开始的时候,其实大部分厂商都还是只有线性的回声消除。但现在我们一般会在线性回声处理之后再集联一个非线性处理,来解决这些线形处理后的残留回声。非线性建模需要兼顾不同设备、环境是一件很有挑战的事情。
除了传统算法,最近几年也有很多通过机器学习的方式来解决非线性的方案,并起到了比较好的效果。究其复杂性,非线性这块我们将会在下一讲中再继续展开来聊聊。
好的,我们这里总结一下。由于采集和播放设备的耦合,在实时音频互动领域,回声消除是实时音频链路中重要的一环。常见的回声消除流程包括双讲检测、延迟估计、线性回声消除、非线性回声消除等步骤。这里可以用一个流程图(图2)来总结一下,帮助你整体理解AEC的算法过程。
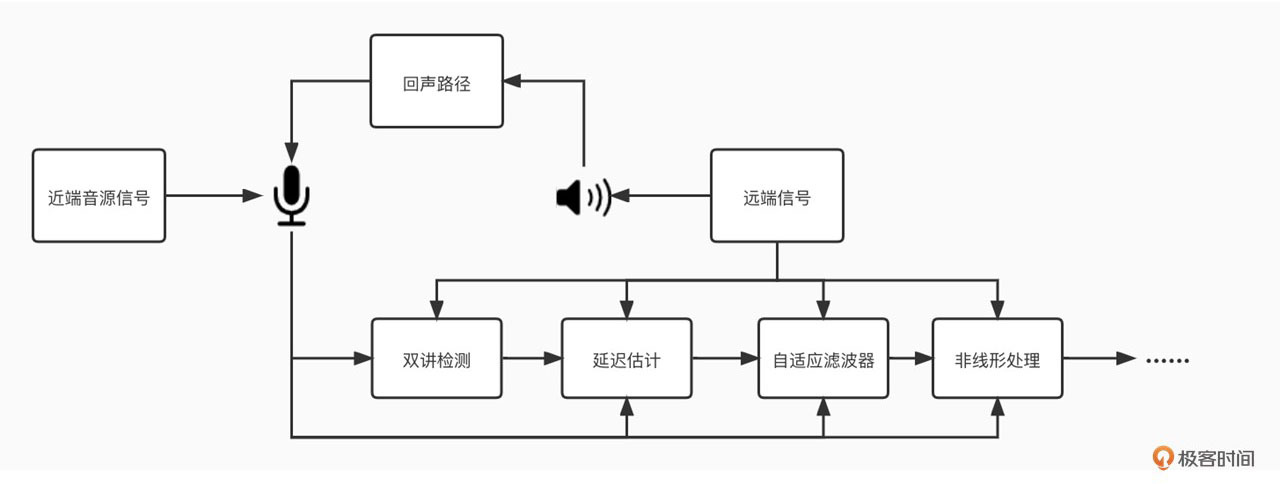
回声消除发展了几十年,依然还是一个比较热门的研究领域。究其原因还是因为它的复杂性,设备、环境、工程部署的实时性甚至是其它的音频模块都可能会对回声消除的效果产生影响。我们一般把回声消除模块放在紧挨着音频采集模块的位置。也就是说,做完了AEC再做降噪、增益调整等其它的音频模块。这样可以尽量减少音频处理对回声路径的复杂性的增加。
回声消除算法其实是在已知一个音源信号的条件下,在多音源混合的音频中消除这一音源。所以有的时候回声消除也被用来做一些音源分离的事情。比如一首歌你已经有伴奏的情况下,对人声和伴奏混合在一起的歌曲,用回声消除就可以提取到清唱(也就是没有伴奏的纯人声)。
有的时候设备或者App在使用过程中还是会频繁地出现回声泄漏,但是带上耳机似乎大部分回声问题就可以解决,这背后的原理是什么呢?
你可以把你的答案和疑惑写下来,分享到留言区,与我一起讨论。我们下节课再见。