你好,我是李江。
在前面几节课里面我们对视频编码的原理、帧内编码和帧间编码都做了详细的介绍。我们知道,通过帧内编码可以去除空间冗余,通过帧间编码可以去除时间冗余,而为了分离图像块的高频和低频信息从而去除视觉冗余,我们需要做DCT变换和量化。
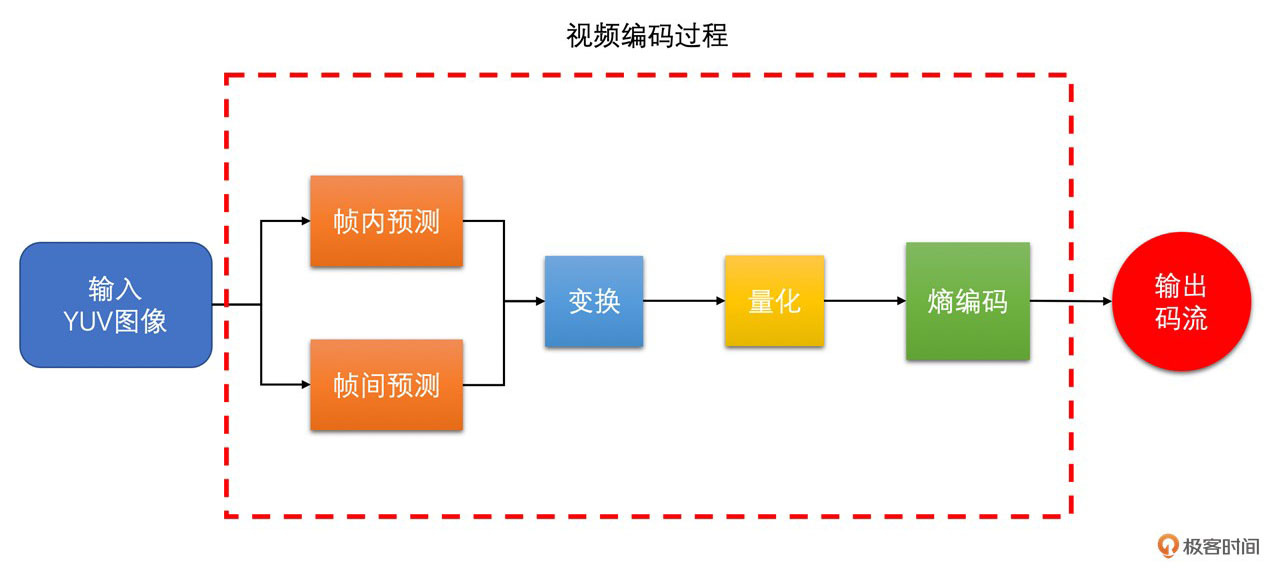
为了让你更透彻地了解视频编码中的DCT变换和量化的原理,在这节课里面,我们会对DCT变换和量化的过程做一个深入的探讨。通过下图你可以很清楚地看到视频编码的过程,并且能够更直观地感受DCT变换和量化在整个视频编码过程中的重要性。

由于DCT变换和量化过程是一个跟数学比较相关的过程,且大多数是数学计算。因此今天的课程中数学公式和计算过程相对会多一些。但是总体来说难度不是很大。
下面我们就先来讨论一下常规的视频编码中的DCT变换和量化,看看它是怎么去除一部分高频信息来达到去除视觉冗余的。并且,由于H264中用到的DCT变换和量化跟常规的DCT变换和量化有一些区别,其主要在于H264使用整数变换代替常规的DCT变换,并将DCT变换中的一部分计算整合到量化中,从而减少浮点运算漂移问题。因此,我们还会对H264中的DCT变换和量化做一下介绍,最后对比一下H264中的变换和量化与常规的变换和量化的区别。
通过前面的学习,我们知道DCT变换和量化的目的是去除视觉冗余。接下来让我们看一下常规视频编码中DCT变换和量化是如何实现这一目的的。
DCT变换,就是离散余弦变换。它能够将空域的信号(对于图像来说,空域就是你平时看到的图像)转换到频域(对于图像来说,就是将图像做完DCT变换之后的数据)上表示,并能够比较好的去除相关性。其主要用于视频压缩领域。现在常用的视频压缩算法中基本上都有DCT变换。
在视频编码原理那节课中我们也讲过,图片经过DCT变换之后,低频信息集中在左上角,而高频信息则分散在其它的位置。通常情况下,图片的高频信息多但是幅值比较小。高频信息主要描述图片的边缘信息。
由于人眼的视觉敏感度是有限的,有的时候我们去除了一部分高频信息之后,人眼看上去感觉区别并不大。因此,我们可以先将图片DCT变换到频域,然后再去除一些高频信息。这样我们就可以减少信息量,从而达到压缩的目的。
DCT变换本身是无损的,同时也是可逆的。我们可以通过DCT变换将图片从空域转换到频域,也可以通过DCT反变换将图片从频域转回到空域。下面我们来看一下DCT变换的公式。
一维DCT变换公式如下,其中f(i)是指第i个样点的信号值,N代表信号样点的总个数。

二维DCT变换公式如下,其中f(i, j)是指第(i, j)位置的样点的信号值,N代表信号样点的总个数。

一般在编码标准中图像是进行二维DCT变换的,因为图像是个二维信号。但是实际上在代码里面我们经常将二维DCT变换转换成两个一维DCT变换来进行。
在视频压缩中,DCT变换是在帧内预测和帧间预测之后进行的。也就是说,DCT变换其实是对残差块做的。我们在编码时会将图像划分成一个个宏块,而宏块又可以划分成一个个子块。那DCT变换是在宏块上进行还是在子块上进行呢?
其实,通常情况下DCT变换是在4x4的子块上进行的(也可以在8x8子块上进行,但是只有在扩展profile才支持,由于原理是一样的,因此这里不再展开讨论),即便预测时并没有对宏块再做划分。也就是说,不管宏块有没有被划分到4x4的子块,我们在做DCT变换时,都是在一个个4x4块上进行的。如下图所示:

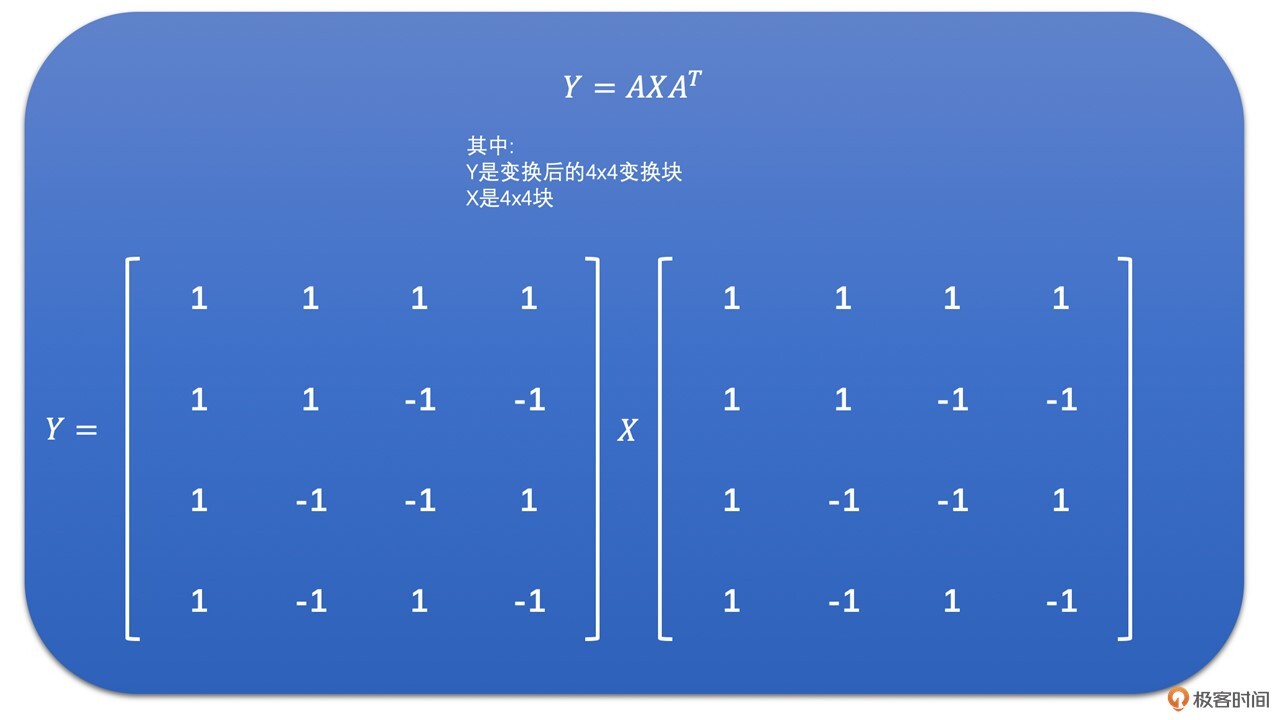
好了,如果我们将上面的DCT变换公式用在4x4的变换块上,则4x4的DCT变换就可以通过下面的4x4的矩阵乘法来表示了。
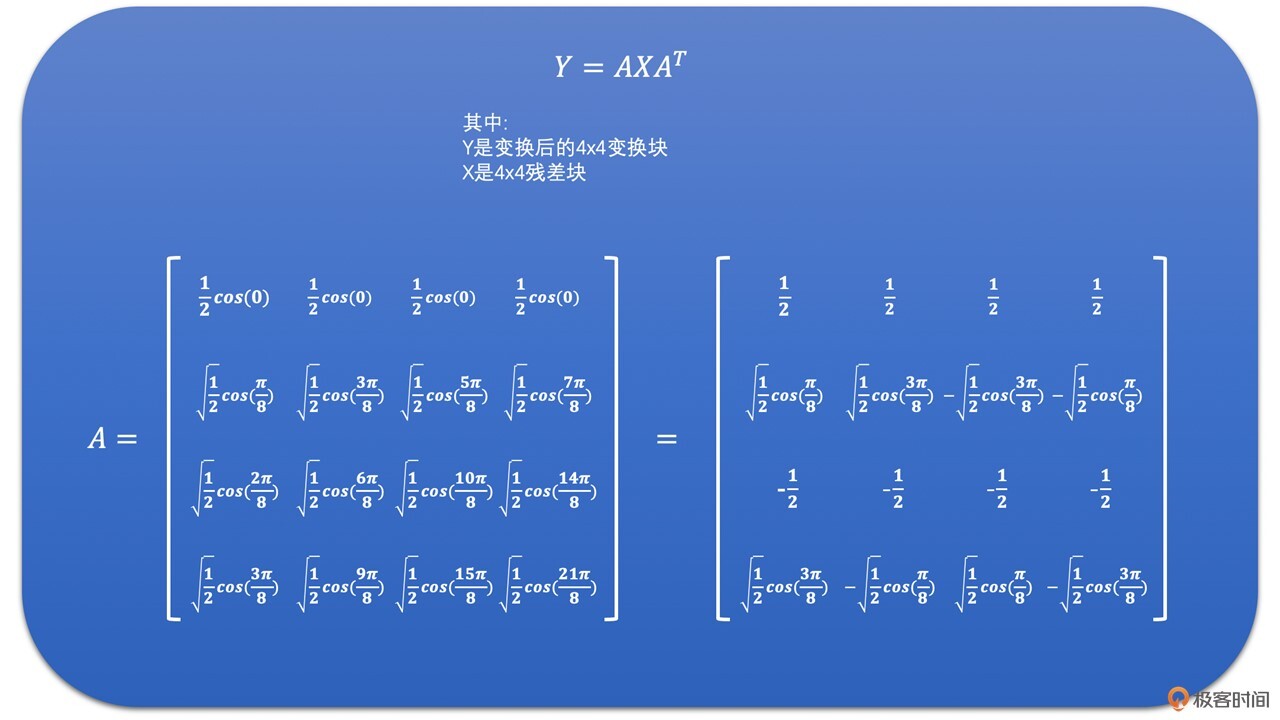
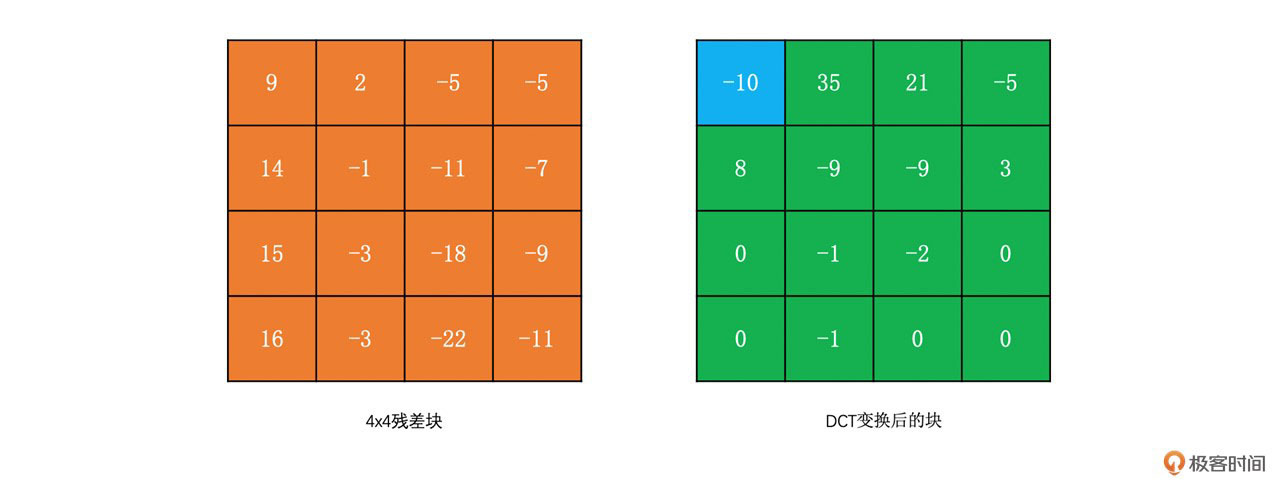
为了让你更好地理解DCT变换,我们通过下面的例子来看一下4x4的残差块的DCT变换结果。我们称左上角的系数为DC系数,而其它系数为AC系数。
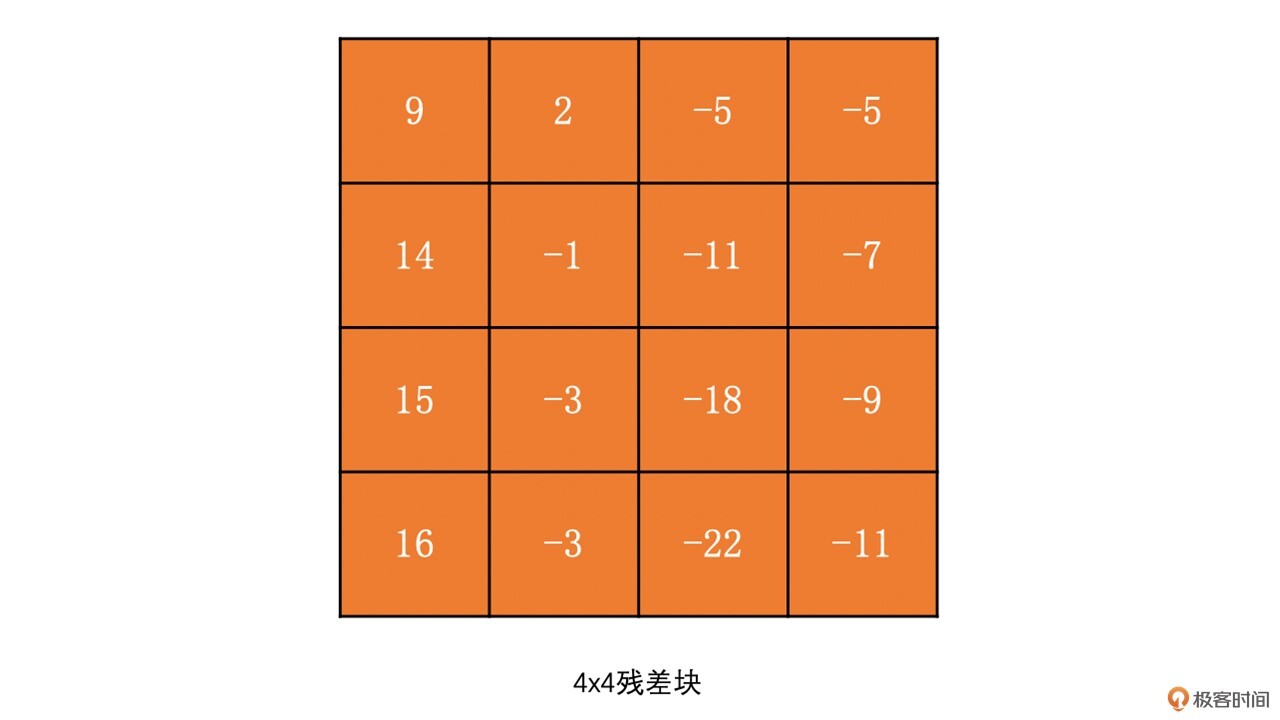
对这个4x4的残差块运用公式,可得:
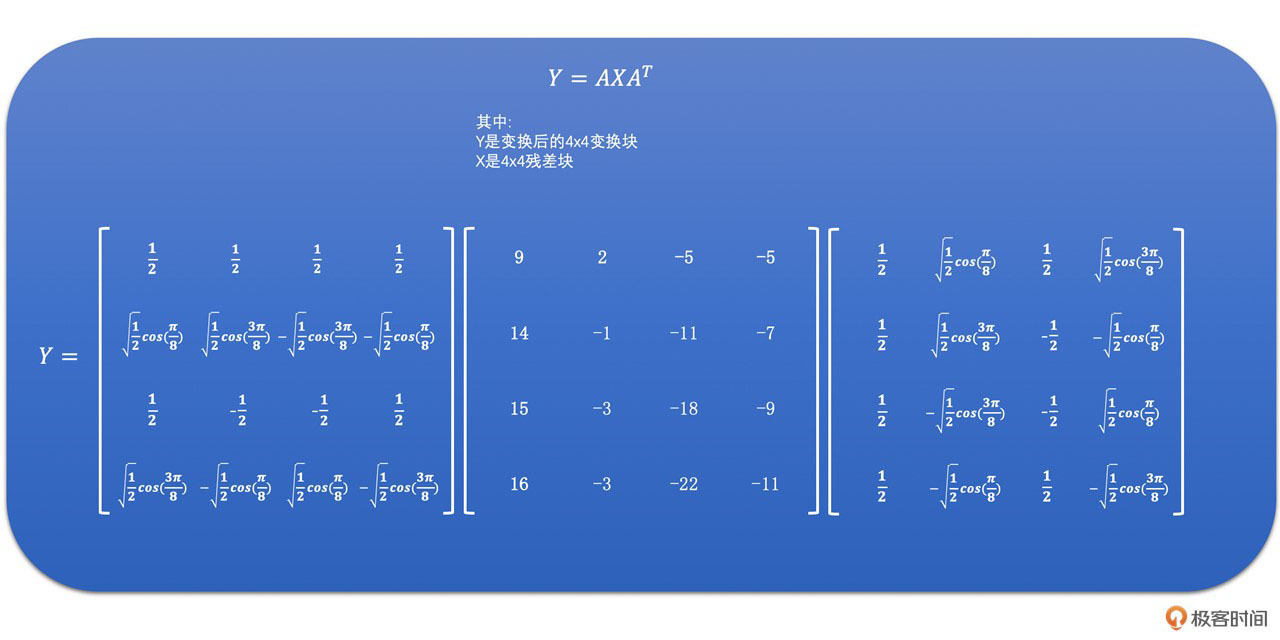
我们可以得到下面的图:
从上面DCT变换的公式和矩阵表示方式中,我们可以看到,DCT变换的计算过程中涉及到了cos函数。那也就是说计算的过程中一定涉及到了浮点运算。而浮点运算计算速度比较慢。那有没有什么运算可以将图像块比较快速的转换到频域呢?答案肯定是有的。前面我们其实已经讲到过,那就是Hadamard变换,也叫哈达玛变换。
在视频编码过程中,Hadamard变换也经常会用到。前面我们在帧内预测的率失真优化的模式选择里就讲到过,Hadamard变换可以代替DCT变换将残差块快速转换到频域,以便用来估计一下当前块编码之后的大小。
其实在H264的亮度16x16帧内预测块和色度8x8预测块中也会使用到Hadamard变换。稍后我们会在H264中的DCT变换和量化部分对它进行简单介绍。下面我们先来看一下Hadamard变换的矩阵表示形式。
你是不是可以看到,Hadamard变换是没有浮点运算的?因此其计算速度很快,并且也能够将图像块从空域变换到频域。因此,我们可以用它一定程度上粗略的代替DCT变换,从而用来简化运算。
好了,现在我们知道了如何通过DCT变换和Hadamard变换将残差块从空域转换到频域。接下来我们看看在常规视频编码中量化是如何做到通过去除一部分高频信息来最终达到去除视觉冗余的。
前面我们讲了,我们将图像块变换到频域之后,AC系数比较多,但是一般幅值比较小。并且,我们可以去除一些AC系数,达到压缩图像的目的,同时人眼看起来差距不大。这个去除AC系数的操作是什么呢?很明显就是量化了。
其实量化的操作并不是针对AC系数去做的,DC系数也同样会做量化,只是通常情况下,DC系数比较大,从而量化后变换为0的概率比AC系数要小。量化操作其实非常简单,就是除法操作。计算公式如下:

在量化过程中,最重要的就是QStep(用户一般接触到的是QP,两者可以查表转换)。
其中,在H264中QP和QStep之间的转换表格如下:
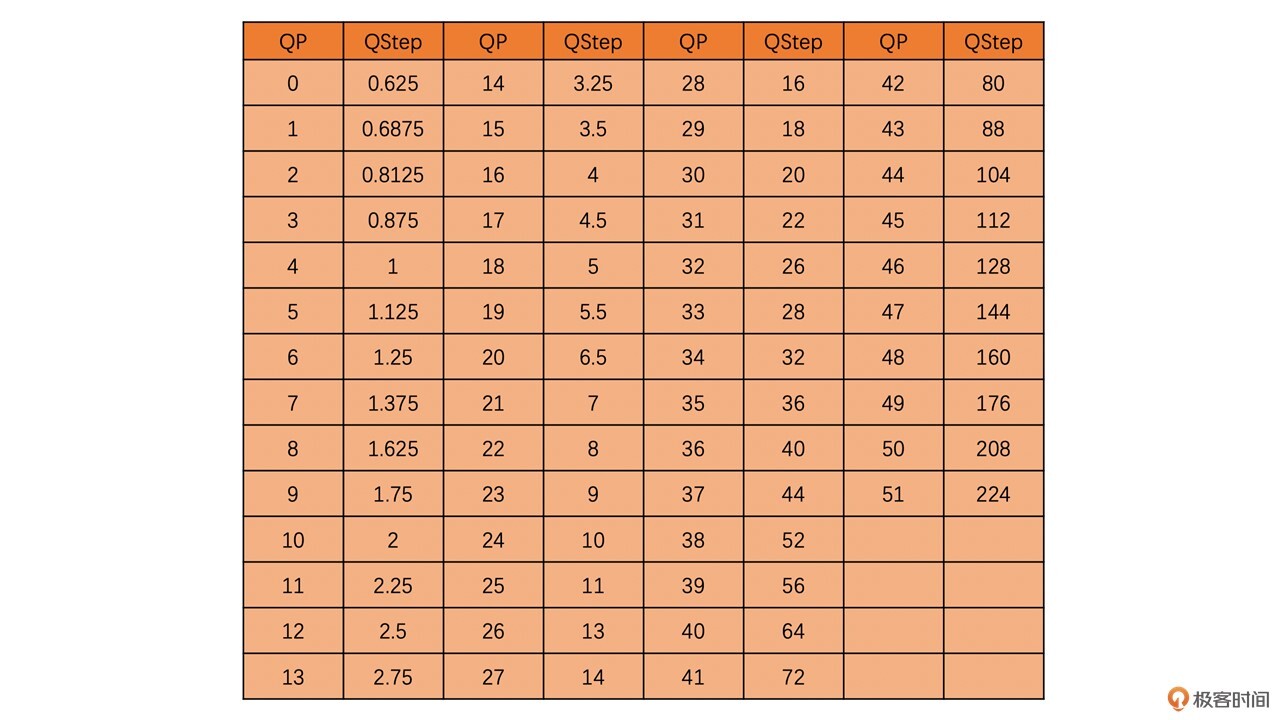
通常QStep值越大,DC系数和AC系数被量化成0的概率也就越大,从而压缩程度就越大,但是丢失的信息也就越多。这个值太大了会造成视频出现一个个块状的效应,且严重的时候看起来像马赛克一样;这个值比较小的话,压缩程度也会比较小,从而图像失真就会比较小,但是压缩之后的码流大小就会比较大。
我们通过一个例子来看一下量化的结果。
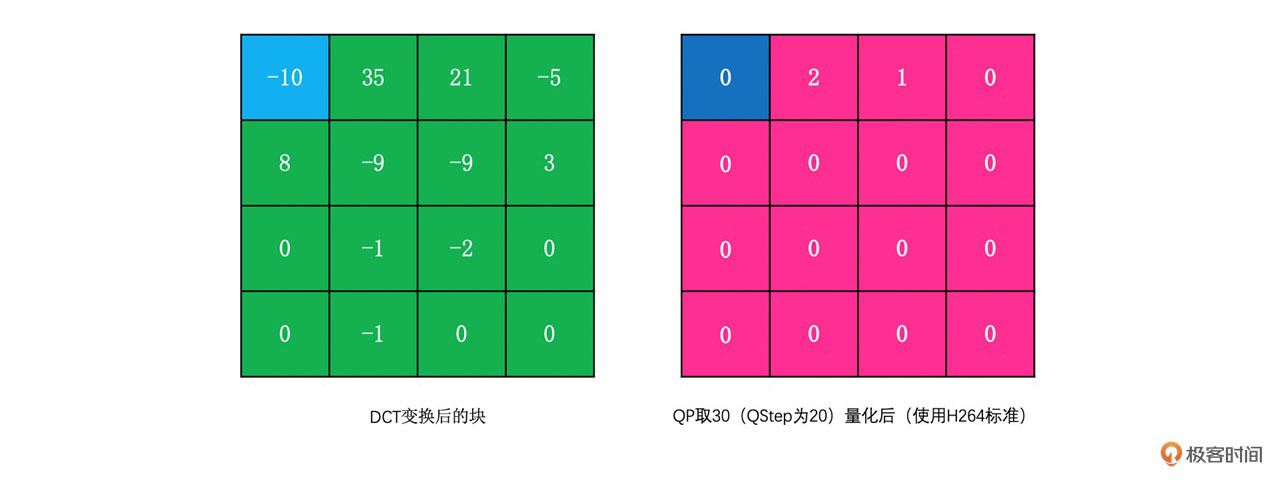
这就是常规的变换和量化的计算过程。实际上H264里面的变换和量化是这样的吗?原理上是的,但是实际计算过程变了。因为DCT变换过程中涉及到浮点运算,在不同机器上解码会因为精度问题产生漂移导致误差。同样,量化过程有除法运算,大多数时候其结果还是浮点型的数字,在不同机器上解码也会有误差。
H264为了减少这种浮点型运算漂移带来的误差,将DCT变换改成了整数变换,DCT变换中的浮点运算和量化过程合并,这样就只有一次浮点运算过程,以此来减少不同机器上浮点运算产生的误差。下面我们来看看H264中的变换和量化。
我们知道常规的DCT变换的矩阵计算方式如下:
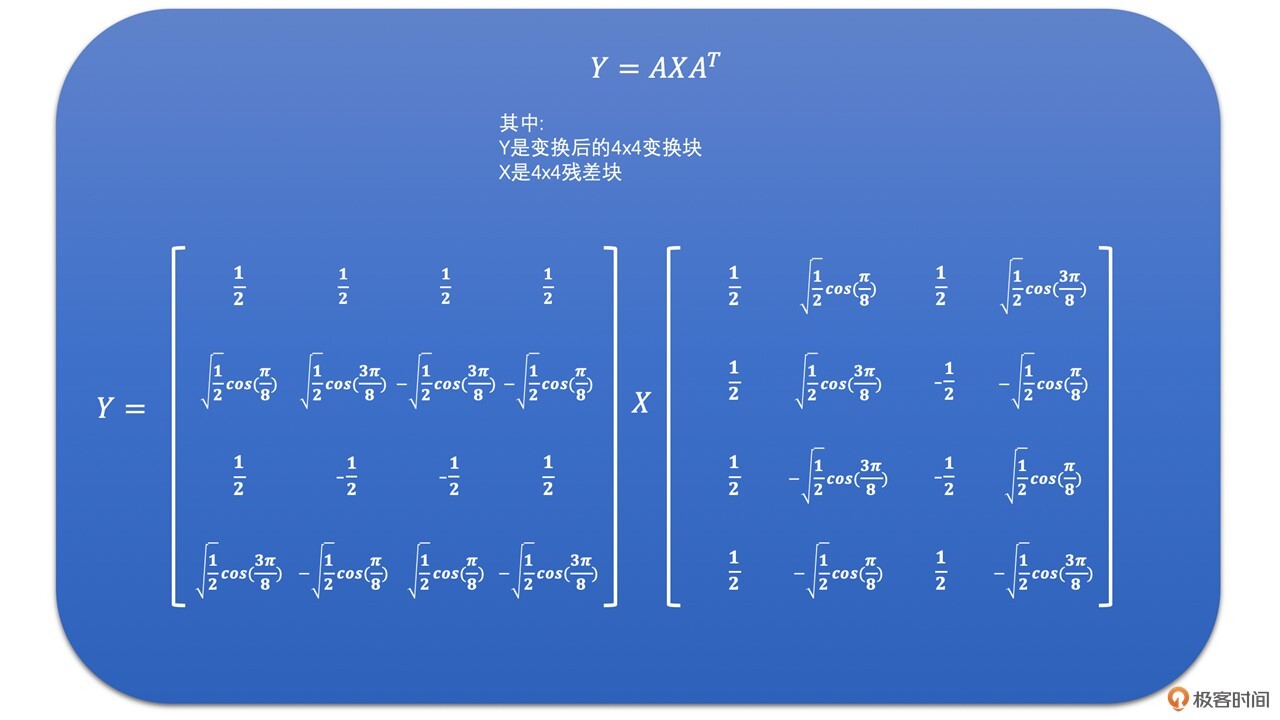
而在H264中,我们通过下面的推导过程,将DCT变换一步步修改为整数变换。最后H264中的DCT变换就变成了整数变换。其矩阵的计算方式如下:
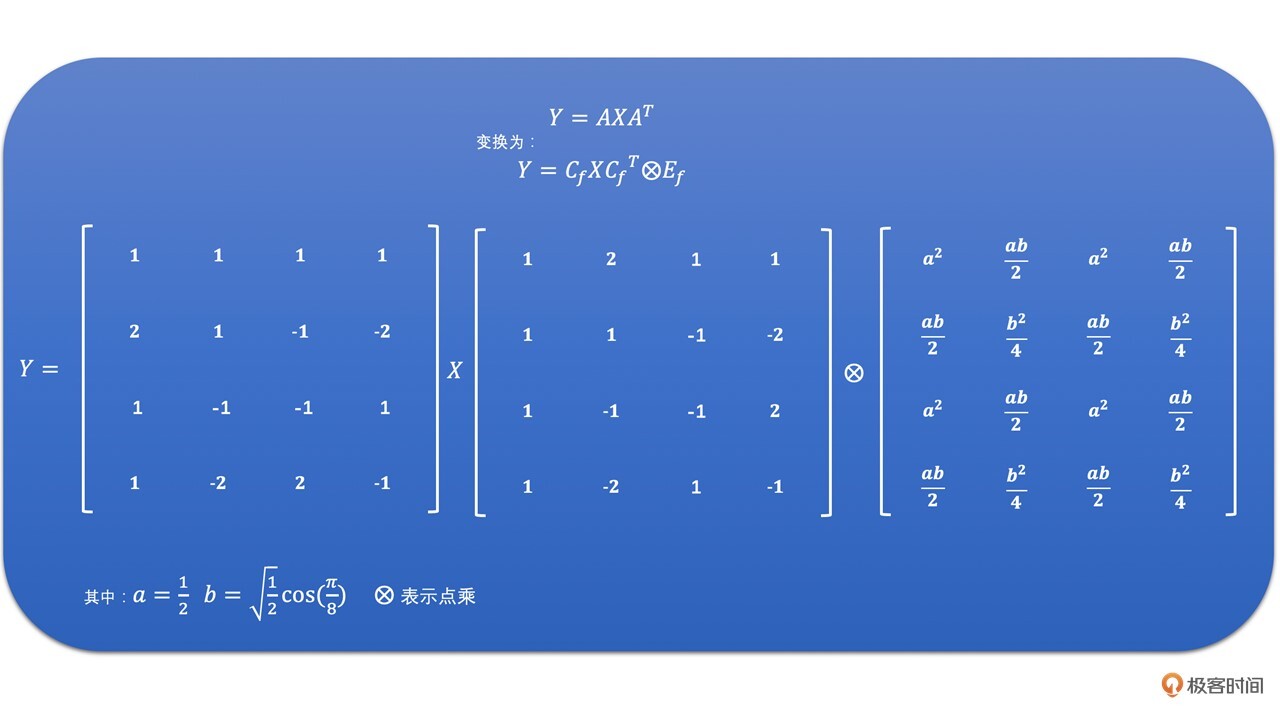
我们将点乘左边的部分取出来,就是H264中的整数变换了。公式如下:
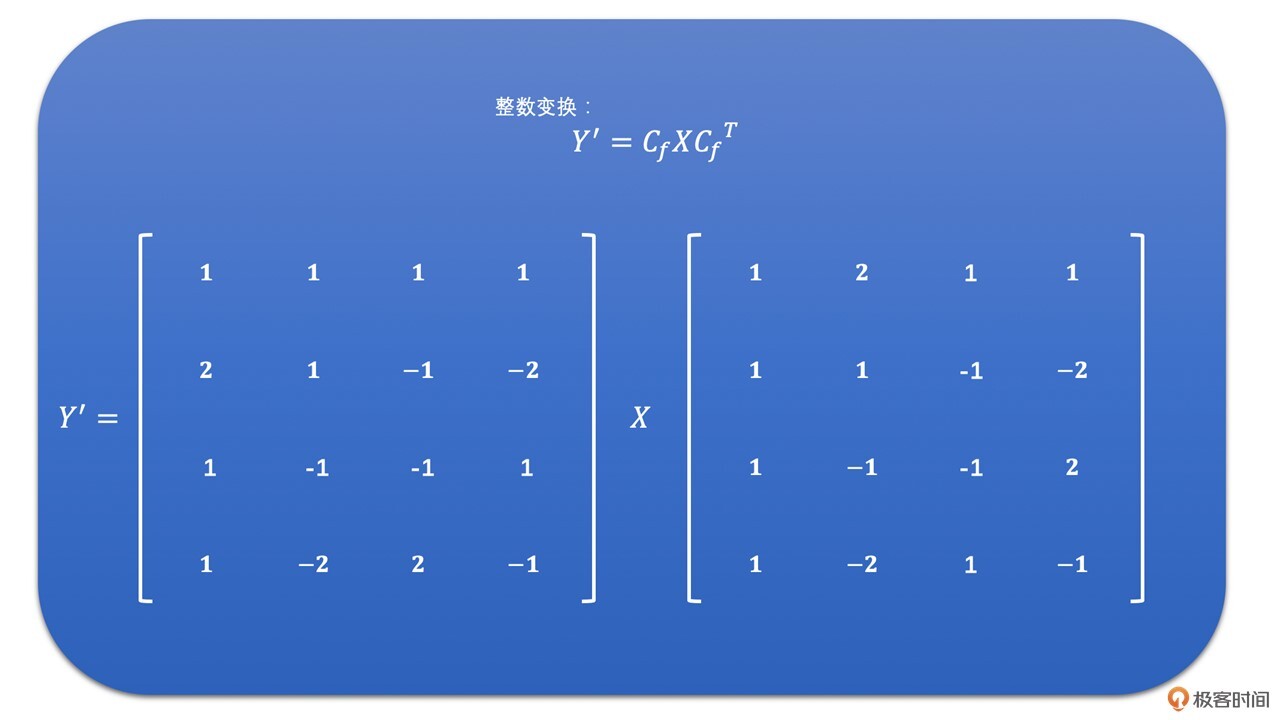
我们同样使用上面DCT变换的例子来做一下整数变换。其结果如下:
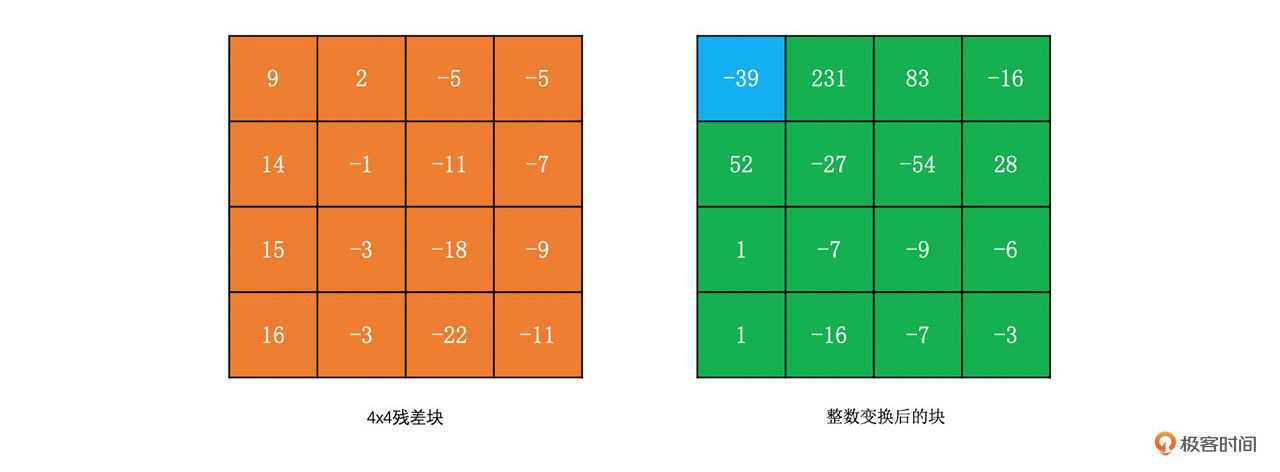
在前面整数变换里,DCT变换中的点乘部分被拿出来了,这一部分的计算被合并到了H264的量化过程中。因此H264的量化过程如下所示:

其中,MF我们一般都是通过表格查询得到。表格如下。其中,对于QP大于5的情况,使用QP = QP % 6进行查询。
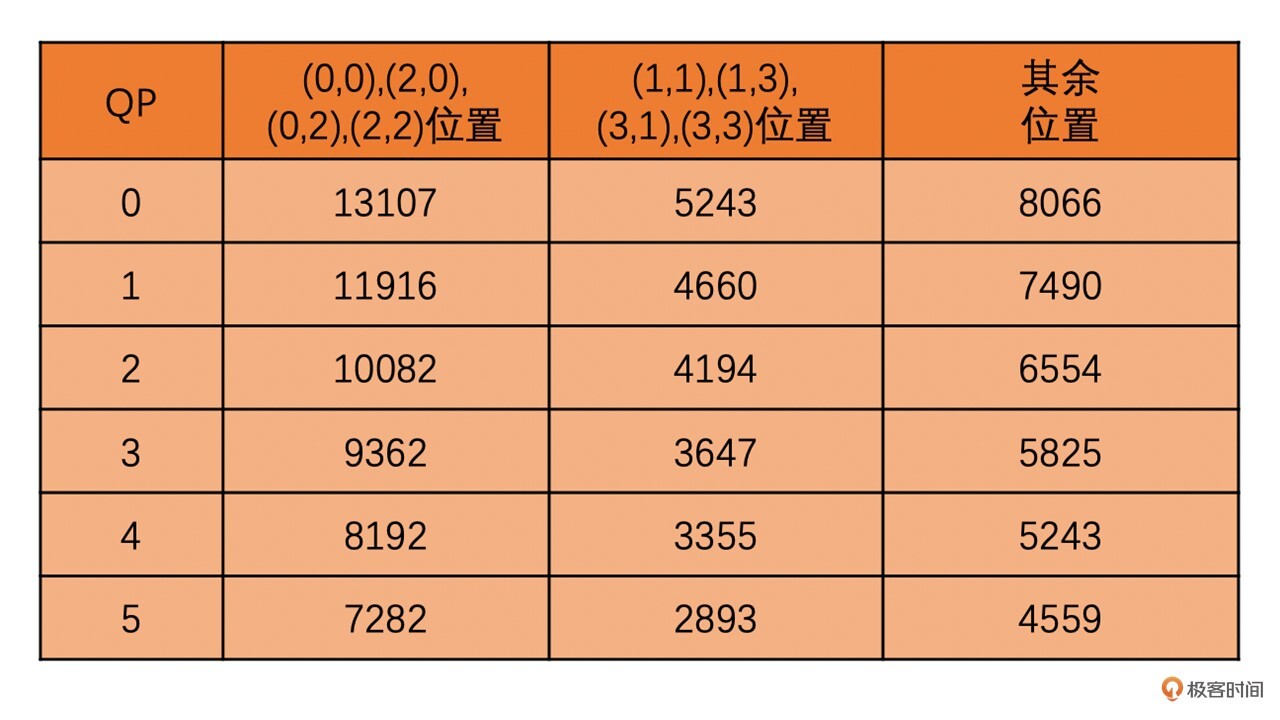
同样,上面整数变换之后,我们用H264的量化公式对其进行量化后得到的结果如下:
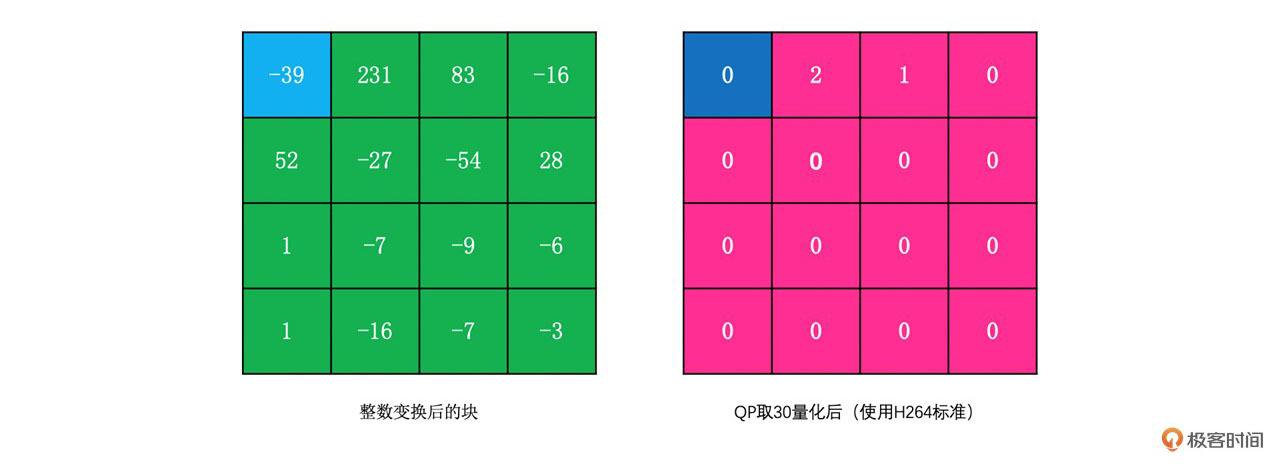
我们可以看到虽然H264的DCT变换和量化过程跟常规的DCT变换和量化不一样,但是最后量化的结果其实还是一样的。这也是符合预期的。毕竟它们的“目的地”还是一样的,只是“走的路”稍微有些不同而已。
好了,这就是H264中的DCT变换和量化的基本原理。接下来我们来看看H264各模式块的DCT变换和量化过程具体是怎么样的。
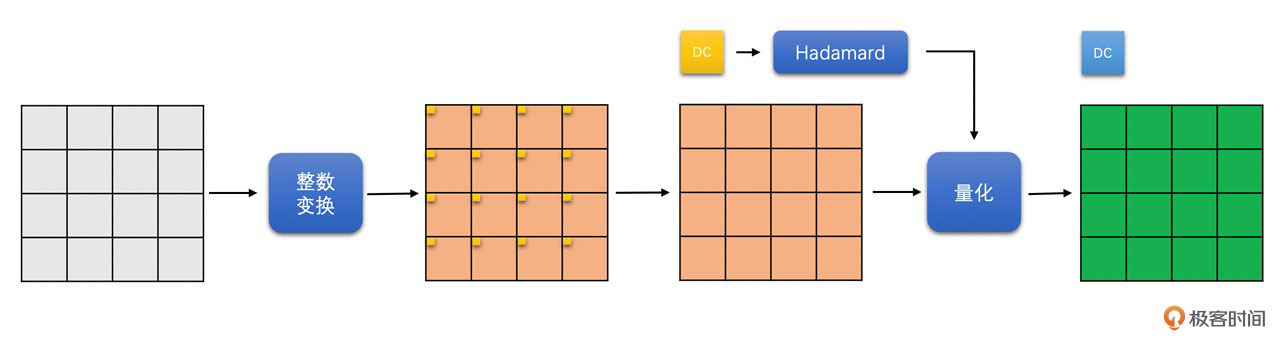
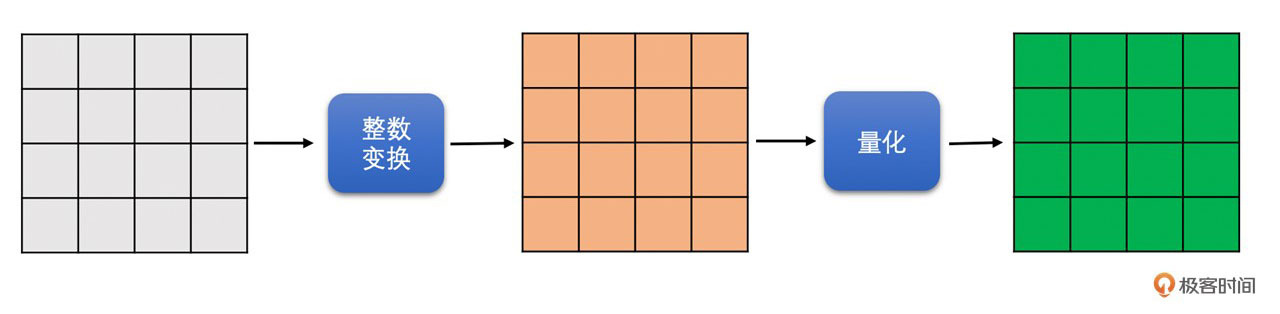
3. 色度块
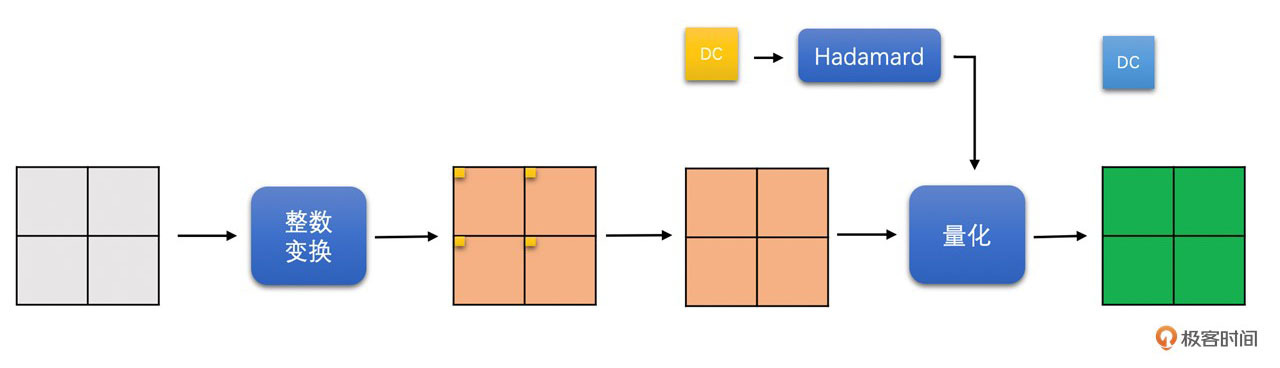
对于YUV420图像,色度块大小是8x8。我们先将8x8色度块划分成4个4x4的小块做整数变换。变换之后将4个小块的DC系数拿出来,组成一个2x2的DC块,再对这个2x2的DC块进行Hadamard变换。最后总体进行量化操作。
我们今天一开始主要讲解了DCT变换的基本原理。DCT变换主要是将图像从空域转换到频域,并将图像的高频和低频信息分离开来。虽然高频信息数据多,但是幅值比较小。这样高频信息在量化的过程中能够比较容易被减少。这样可以比较有效地减少图像的视觉冗余,从而达到压缩的目的。
接着,我们简单地介绍了一下量化的原理。量化其实就是一个除法操作。通过除法操作就可以将幅值变小,而高频信息幅值比较小,就比较容易被量化成0,这样就能够达到压缩的目的。
在讲变换的原理的时候,我们还讲到了一个前面提到了好几次的Hadamard变换。Hadamard变换在H264的16x16帧内亮度块和8x8色度块中会被用到。但是Hadamard在率失真优化做模式选择的时候使用的更多。基本上各种视频编码都或多或少会用到它来做率失真优化。
在H264标准中,我们不会直接使用标准的DCT变换和量化。为了减少多次浮点型运算在解码端产生漂移的问题,H264使用整数变换代替DCT变换。DCT变换中的浮点运算部分跟量化过程进行合并,将两次浮点型运算变成一次,从而减少误差。
在最后,我们简单介绍了H264标准中不同模式亮度块和色度块的DCT变换和量化的过程。其中需要注意的就是亮度16x16帧内预测块和色度8x8的DC系数会单独拿出来组成一个新的DC块,我们会先对这个DC块进行Hadamard变换之后再做量化操作。
为什么我们在率失真优化的过程中会用Hadamard变换之后的块做大小预估?
你可以把你的答案和疑惑写下来,分享到留言区,与我一起讨论。下节课再见。