数据表一共包括了32个字段,代表的含义如下:
讲完了SVM的原理之后,今天我来带你进行SVM的实战。
在此之前我们先来回顾一下SVM的相关知识点。SVM是有监督的学习模型,我们需要事先对数据打上分类标签,通过求解最大分类间隔来求解二分类问题。如果要求解多分类问题,可以将多个二分类器组合起来形成一个多分类器。
上一节中讲到了硬间隔、软间隔、非线性SVM,以及分类间隔的公式,你可能会觉得比较抽象。这节课,我们会在实际使用中,讲解对工具的使用,以及相关参数的含义。
在Python的sklearn工具包中有SVM算法,首先需要引用工具包:
from sklearn import svm
SVM既可以做回归,也可以做分类器。
当用SVM做回归的时候,我们可以使用SVR或LinearSVR。SVR的英文是Support Vector Regression。这篇文章只讲分类,这里只是简单地提一下。
当做分类器的时候,我们使用的是SVC或者LinearSVC。SVC的英文是Support Vector Classification。
我简单说一下这两者之前的差别。
从名字上你能看出LinearSVC是个线性分类器,用于处理线性可分的数据,只能使用线性核函数。上一节,我讲到SVM是通过核函数将样本从原始空间映射到一个更高维的特质空间中,这样就使得样本在新的空间中线性可分。
如果是针对非线性的数据,需要用到SVC。在SVC中,我们既可以使用到线性核函数(进行线性划分),也能使用高维的核函数(进行非线性划分)。
如何创建一个SVM分类器呢?
我们首先使用SVC的构造函数:model = svm.SVC(kernel=‘rbf’, C=1.0, gamma=‘auto’),这里有三个重要的参数kernel、C和gamma。
kernel代表核函数的选择,它有四种选择,只不过默认是rbf,即高斯核函数。
linear:线性核函数
poly:多项式核函数
rbf:高斯核函数(默认)
sigmoid:sigmoid核函数
这四种函数代表不同的映射方式,你可能会问,在实际工作中,如何选择这4种核函数呢?我来给你解释一下:
线性核函数,是在数据线性可分的情况下使用的,运算速度快,效果好。不足在于它不能处理线性不可分的数据。
多项式核函数可以将数据从低维空间映射到高维空间,但参数比较多,计算量大。
高斯核函数同样可以将样本映射到高维空间,但相比于多项式核函数来说所需的参数比较少,通常性能不错,所以是默认使用的核函数。
了解深度学习的同学应该知道sigmoid经常用在神经网络的映射中。因此当选用sigmoid核函数时,SVM实现的是多层神经网络。
上面介绍的4种核函数,除了第一种线性核函数外,其余3种都可以处理线性不可分的数据。
参数C代表目标函数的惩罚系数,惩罚系数指的是分错样本时的惩罚程度,默认情况下为1.0。当C越大的时候,分类器的准确性越高,但同样容错率会越低,泛化能力会变差。相反,C越小,泛化能力越强,但是准确性会降低。
参数gamma代表核函数的系数,默认为样本特征数的倒数,即gamma = 1 / n_features。
在创建SVM分类器之后,就可以输入训练集对它进行训练。我们使用model.fit(train_X,train_y),传入训练集中的特征值矩阵train_X和分类标识train_y。特征值矩阵就是我们在特征选择后抽取的特征值矩阵(当然你也可以用全部数据作为特征值矩阵);分类标识就是人工事先针对每个样本标识的分类结果。这样模型会自动进行分类器的训练。我们可以使用prediction=model.predict(test_X)来对结果进行预测,传入测试集中的样本特征矩阵test_X,可以得到测试集的预测分类结果prediction。
同样我们也可以创建线性SVM分类器,使用model=svm.LinearSVC()。在LinearSVC中没有kernel这个参数,限制我们只能使用线性核函数。由于LinearSVC对线性分类做了优化,对于数据量大的线性可分问题,使用LinearSVC的效率要高于SVC。
如果你不知道数据集是否为线性,可以直接使用SVC类创建SVM分类器。
在训练和预测中,LinearSVC和SVC一样,都是使用model.fit(train_X,train_y)和model.predict(test_X)。
在了解了如何创建和使用SVM分类器后,我们来看一个实际的项目,数据集来自美国威斯康星州的乳腺癌诊断数据集,点击这里进行下载。
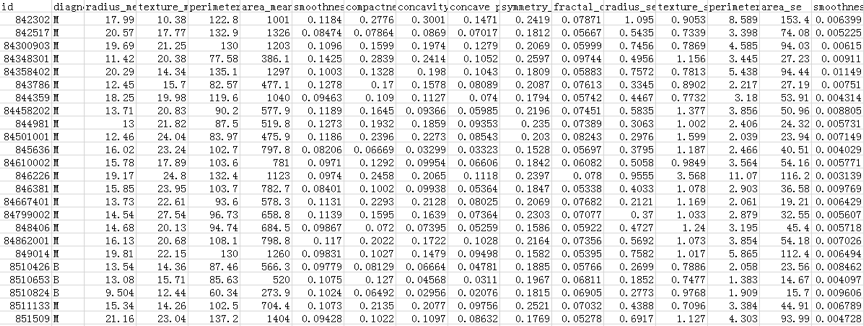
医疗人员采集了患者乳腺肿块经过细针穿刺(FNA)后的数字化图像,并且对这些数字图像进行了特征提取,这些特征可以描述图像中的细胞核呈现。肿瘤可以分成良性和恶性。部分数据截屏如下所示:

数据表一共包括了32个字段,代表的含义如下:
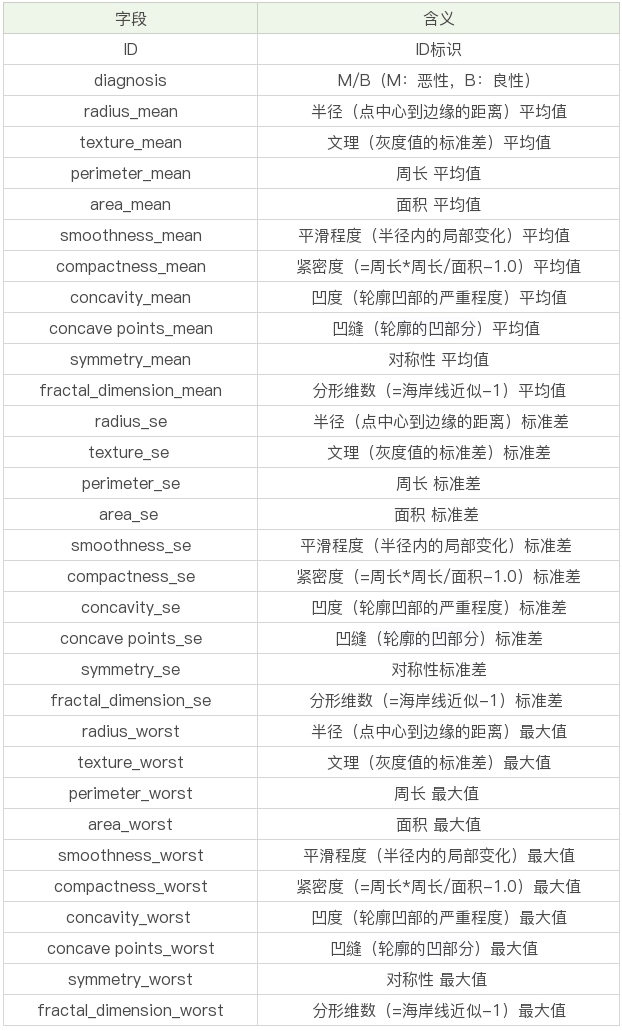
上面的表格中,mean代表平均值,se代表标准差,worst代表最大值(3个最大值的平均值)。每张图像都计算了相应的特征,得出了这30个特征值(不包括ID字段和分类标识结果字段diagnosis),实际上是10个特征值(radius、texture、perimeter、area、smoothness、compactness、concavity、concave points、symmetry和fractal_dimension_mean)的3个维度,平均、标准差和最大值。这些特征值都保留了4位数字。字段中没有缺失的值。在569个患者中,一共有357个是良性,212个是恶性。
好了,我们的目标是生成一个乳腺癌诊断的SVM分类器,并计算这个分类器的准确率。首先设定项目的执行流程:
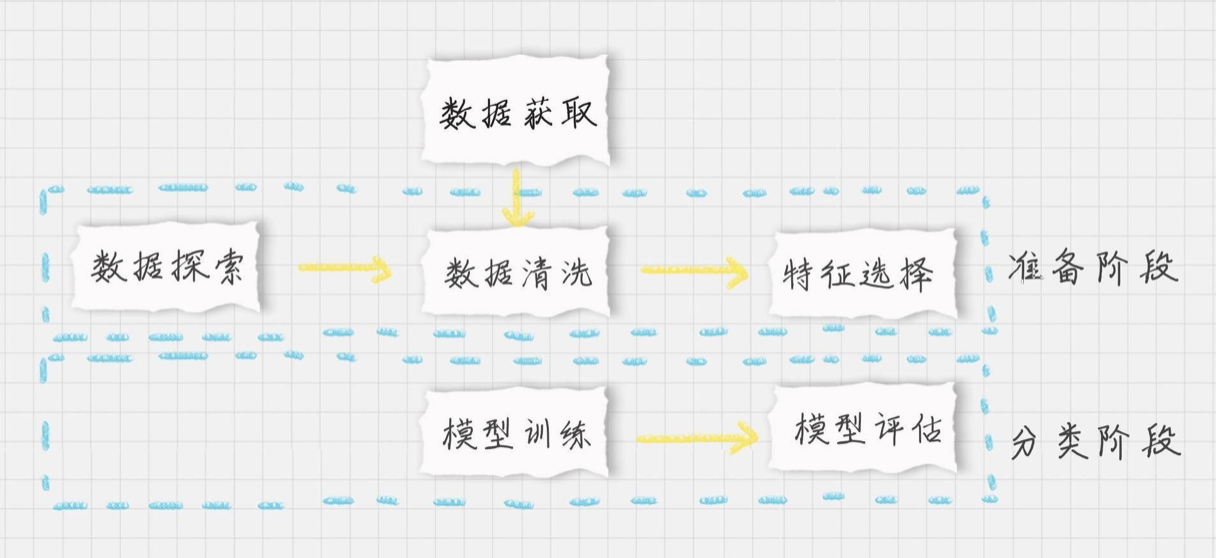
首先我们需要加载数据源;
在准备阶段,需要对加载的数据源进行探索,查看样本特征和特征值,这个过程你也可以使用数据可视化,它可以方便我们对数据及数据之间的关系进一步加深了解。然后按照“完全合一”的准则来评估数据的质量,如果数据质量不高就需要做数据清洗。数据清洗之后,你可以做特征选择,方便后续的模型训练;
在分类阶段,选择核函数进行训练,如果不知道数据是否为线性,可以考虑使用SVC(kernel=‘rbf’) ,也就是高斯核函数的SVM分类器。然后对训练好的模型用测试集进行评估。
按照上面的流程,我们来编写下代码,加载数据并对数据做部分的探索:
# 加载数据集,你需要把数据放到目录中
data = pd.read_csv("./data.csv")
# 数据探索
# 因为数据集中列比较多,我们需要把dataframe中的列全部显示出来
pd.set_option('display.max_columns', None)
print(data.columns)
print(data.head(5))
print(data.describe())
这是部分的运行结果,完整结果你可以自己跑一下。
Index(['id', 'diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean',
'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
'fractal_dimension_se', 'radius_worst', 'texture_worst',
'perimeter_worst', 'area_worst', 'smoothness_worst',
'compactness_worst', 'concavity_worst', 'concave points_worst',
'symmetry_worst', 'fractal_dimension_worst'],
dtype='object')
id diagnosis radius_mean texture_mean perimeter_mean area_mean \
0 842302 M 17.99 10.38 122.80 1001.0
1 842517 M 20.57 17.77 132.90 1326.0
2 84300903 M 19.69 21.25 130.00 1203.0
3 84348301 M 11.42 20.38 77.58 386.1
4 84358402 M 20.29 14.34 135.10 1297.0
接下来,我们就要对数据进行清洗了。
运行结果中,你能看到32个字段里,id是没有实际含义的,可以去掉。diagnosis字段的取值为B或者M,我们可以用0和1来替代。另外其余的30个字段,其实可以分成三组字段,下划线后面的mean、se和worst代表了每组字段不同的度量方式,分别是平均值、标准差和最大值。
# 将特征字段分成3组
features_mean= list(data.columns[2:12])
features_se= list(data.columns[12:22])
features_worst=list(data.columns[22:32])
# 数据清洗
# ID列没有用,删除该列
data.drop("id",axis=1,inplace=True)
# 将B良性替换为0,M恶性替换为1
data['diagnosis']=data['diagnosis'].map({'M':1,'B':0})
然后我们要做特征字段的筛选,首先需要观察下features_mean各变量之间的关系,这里我们可以用DataFrame的corr()函数,然后用热力图帮我们可视化呈现。同样,我们也会看整体良性、恶性肿瘤的诊断情况。
# 将肿瘤诊断结果可视化
sns.countplot(data['diagnosis'],label="Count")
plt.show()
# 用热力图呈现features_mean字段之间的相关性
corr = data[features_mean].corr()
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()
这是运行的结果:
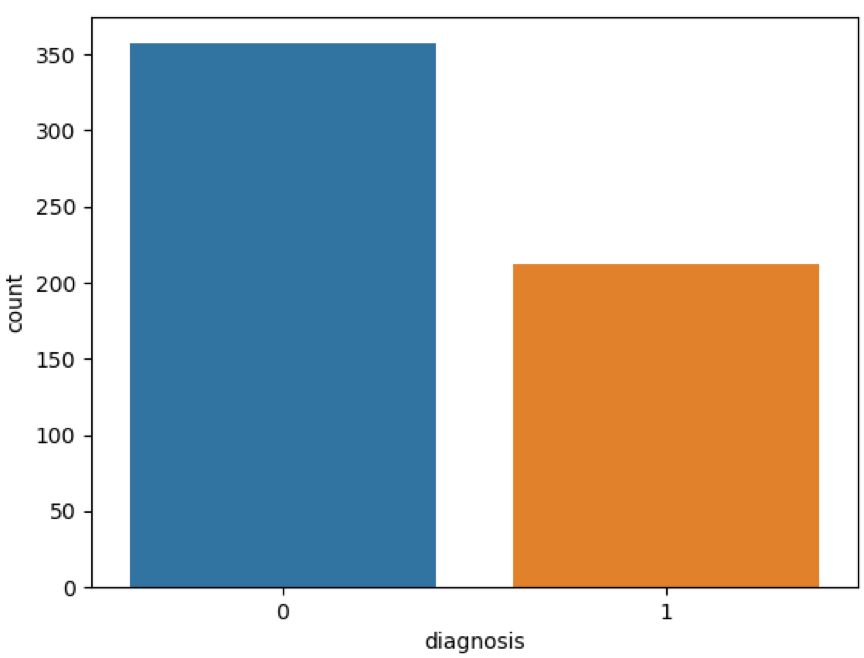
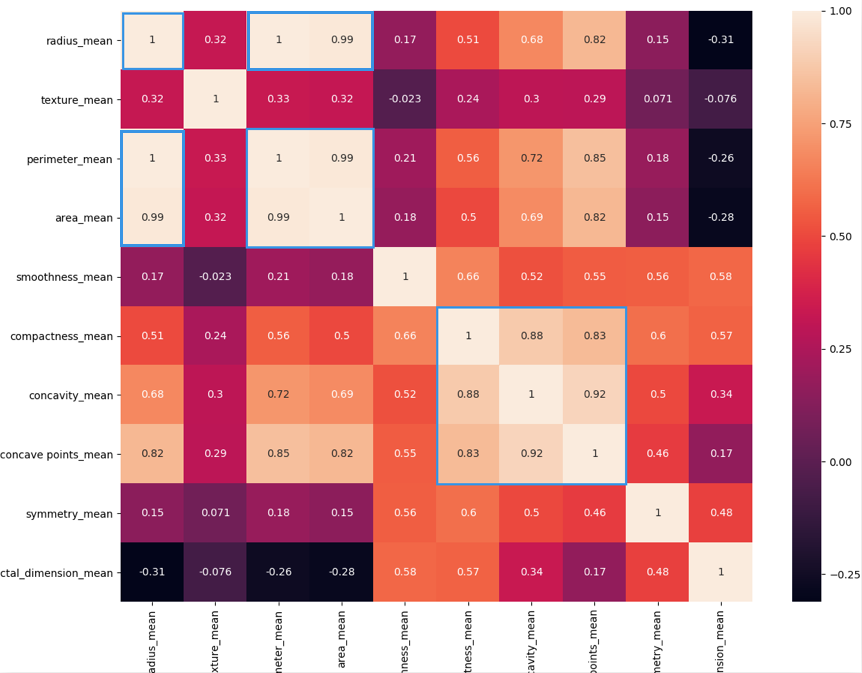
热力图中对角线上的为单变量自身的相关系数是1。颜色越浅代表相关性越大。所以你能看出来radius_mean、perimeter_mean和area_mean相关性非常大,compactness_mean、concavity_mean、concave_points_mean这三个字段也是相关的,因此我们可以取其中的一个作为代表。
那么如何进行特征选择呢?
特征选择的目的是降维,用少量的特征代表数据的特性,这样也可以增强分类器的泛化能力,避免数据过拟合。
我们能看到mean、se和worst这三组特征是对同一组内容的不同度量方式,我们可以保留mean这组特征,在特征选择中忽略掉se和worst。同时我们能看到mean这组特征中,radius_mean、perimeter_mean、area_mean这三个属性相关性大,compactness_mean、daconcavity_mean、concave points_mean这三个属性相关性大。我们分别从这2类中选择1个属性作为代表,比如radius_mean和compactness_mean。
这样我们就可以把原来的10个属性缩减为6个属性,代码如下:
# 特征选择
features_remain = ['radius_mean','texture_mean', 'smoothness_mean','compactness_mean','symmetry_mean', 'fractal_dimension_mean']
对特征进行选择之后,我们就可以准备训练集和测试集:
# 抽取30%的数据作为测试集,其余作为训练集
train, test = train_test_split(data, test_size = 0.3)# in this our main data is splitted into train and test
# 抽取特征选择的数值作为训练和测试数据
train_X = train[features_remain]
train_y=train['diagnosis']
test_X= test[features_remain]
test_y =test['diagnosis']
在训练之前,我们需要对数据进行规范化,这样让数据同在同一个量级上,避免因为维度问题造成数据误差:
# 采用Z-Score规范化数据,保证每个特征维度的数据均值为0,方差为1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)
最后我们可以让SVM做训练和预测了:
# 创建SVM分类器
model = svm.SVC()
# 用训练集做训练
model.fit(train_X,train_y)
# 用测试集做预测
prediction=model.predict(test_X)
print('准确率: ', metrics.accuracy_score(test_y,prediction))
运行结果:
准确率: 0.9181286549707602
准确率大于90%,说明训练结果还不错。完整的代码你可以从GitHub上下载。
今天我带你一起做了乳腺癌诊断分类的SVM实战,从这个过程中你应该能体会出来整个执行的流程,包括数据加载、数据探索、数据清洗、特征选择、SVM训练和结果评估等环节。
sklearn已经为我们提供了很好的工具,对上节课中讲到的SVM的创建和训练都进行了封装,让我们无需关心中间的运算细节。但正因为这样,我们更需要对每个流程熟练掌握,通过实战项目训练数据化思维和对数据的敏感度。
最后给你留两道思考题吧。还是这个乳腺癌诊断的数据,请你用LinearSVC,选取全部的特征(除了ID以外)作为训练数据,看下你的分类器能得到多少的准确度呢?另外你对sklearn中SVM使用又有什么样的体会呢?
欢迎在评论区与我分享你的答案,也欢迎点击“请朋友读”,把这篇文章分享给你的朋友或者同事,一起来交流,一起来进步。