这里有两个概念你需要了解一下。
互联网发展到现在,搜索引擎已经非常好用,基本上输入关键词,都能找到匹配的内容,质量还不错。但在1998年之前,搜索引擎的体验并不好。早期的搜索引擎,会遇到下面的两类问题:
返回结果质量不高:搜索结果不考虑网页的质量,而是通过时间顺序进行检索;
容易被人钻空子:搜索引擎是基于检索词进行检索的,页面中检索词出现的频次越高,匹配度越高,这样就会出现网页作弊的情况。有些网页为了增加搜索引擎的排名,故意增加某个检索词的频率。
基于这些缺陷,当时Google的创始人拉里·佩奇提出了PageRank算法,目的就是要找到优质的网页,这样Google的排序结果不仅能找到用户想要的内容,而且还会从众多网页中筛选出权重高的呈现给用户。
Google的两位创始人都是斯坦福大学的博士生,他们提出的PageRank算法受到了论文影响力因子的评价启发。当一篇论文被引用的次数越多,证明这篇论文的影响力越大。正是这个想法解决了当时网页检索质量不高的问题。
我们先来看下PageRank是如何计算的。
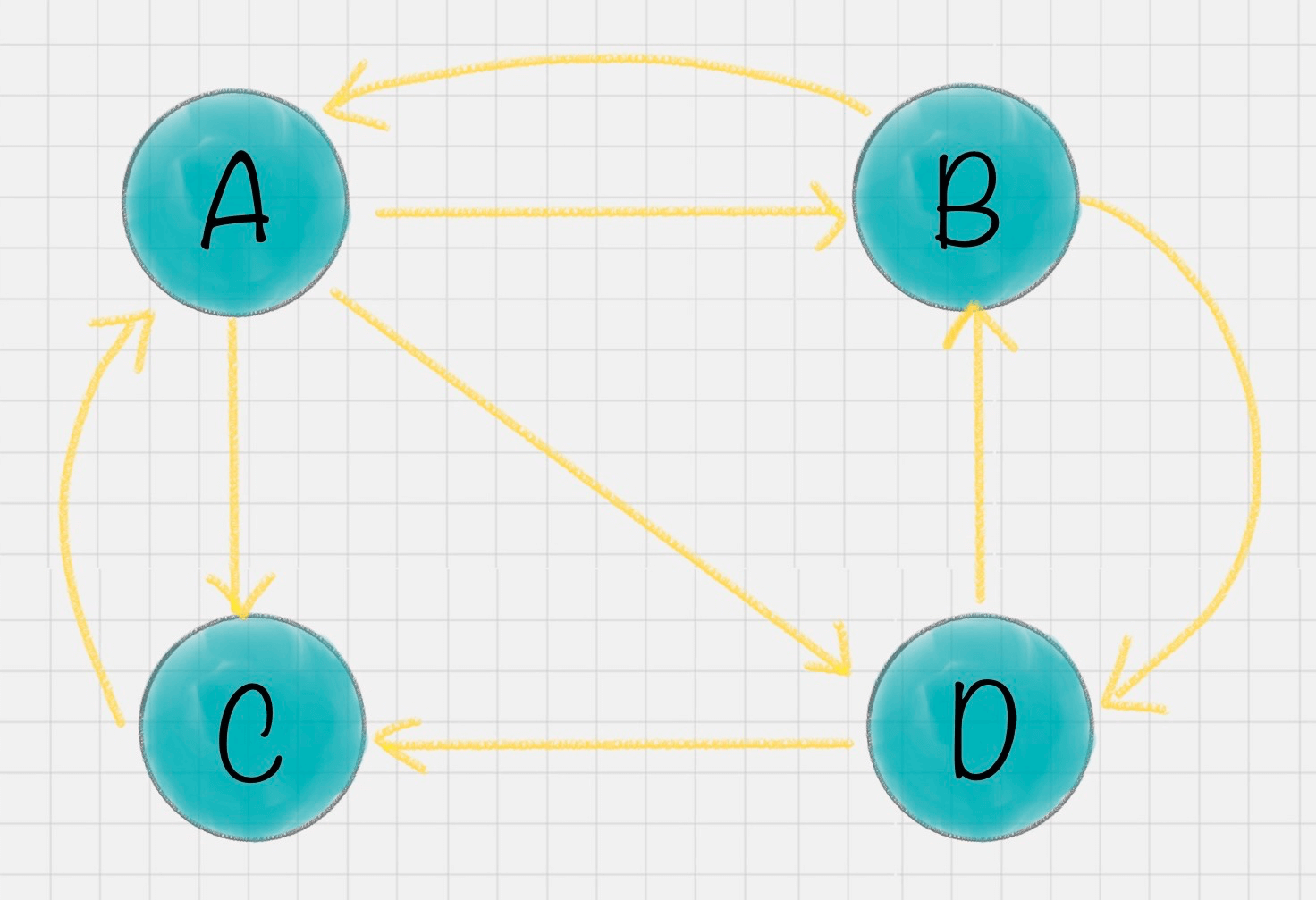
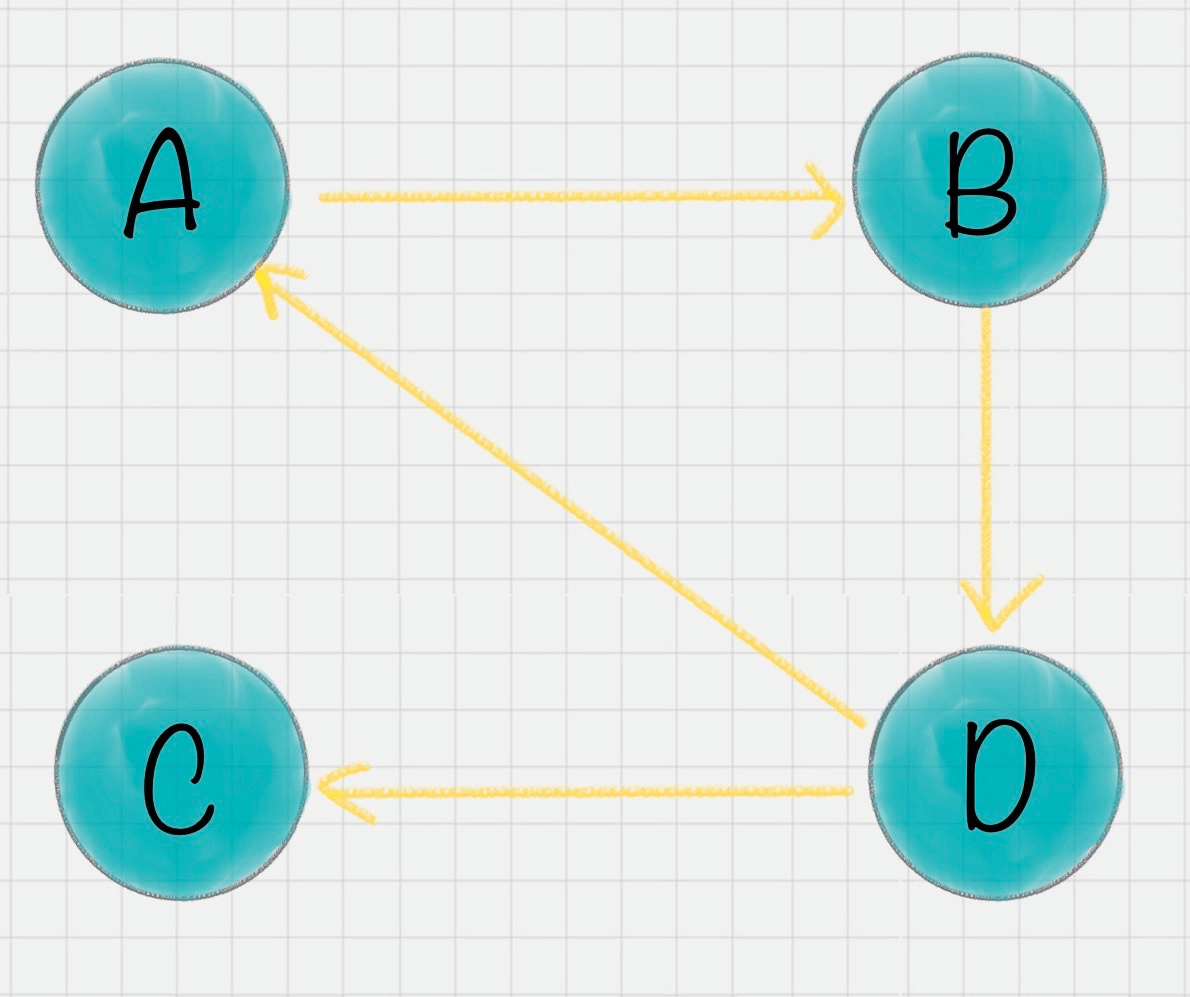
我假设一共有4个网页A、B、C、D。它们之间的链接信息如图所示:

这里有两个概念你需要了解一下。
出链指的是链接出去的链接。入链指的是链接进来的链接。比如图中A有2个入链,3个出链。
简单来说,一个网页的影响力=所有入链集合的页面的加权影响力之和,用公式表示为:
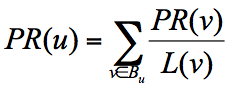
u为待评估的页面,$B_{u}$ 为页面u的入链集合。针对入链集合中的任意页面v,它能给u带来的影响力是其自身的影响力PR(v)除以v页面的出链数量,即页面v把影响力PR(v)平均分配给了它的出链,这样统计所有能给u带来链接的页面v,得到的总和就是网页u的影响力,即为PR(u)。
所以你能看到,出链会给被链接的页面赋予影响力,当我们统计了一个网页链出去的数量,也就是统计了这个网页的跳转概率。
在这个例子中,你能看到A有三个出链分别链接到了B、C、D上。那么当用户访问A的时候,就有跳转到B、C或者D的可能性,跳转概率均为1/3。
B有两个出链,链接到了A和D上,跳转概率为1/2。
这样,我们可以得到A、B、C、D这四个网页的转移矩阵M:

我们假设A、B、C、D四个页面的初始影响力都是相同的,即:
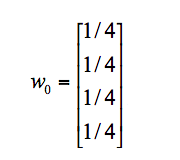
当进行第一次转移之后,各页面的影响力$w_{1}$变为:
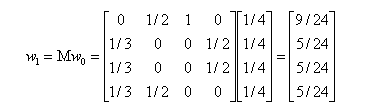
然后我们再用转移矩阵乘以$w_{1}$得到$w_{2}$结果,直到第n次迭代后$w_{n}$影响力不再发生变化,可以收敛到(0.3333,0.2222,0.2222,0.2222),也就是对应着A、B、C、D四个页面最终平衡状态下的影响力。
你能看出A页面相比于其他页面来说权重更大,也就是PR值更高。而B、C、D页面的PR值相等。
至此,我们模拟了一个简化的PageRank的计算过程,实际情况会比这个复杂,可能会面临两个问题:
1.等级泄露(Rank Leak):如果一个网页没有出链,就像是一个黑洞一样,吸收了其他网页的影响力而不释放,最终会导致其他网页的PR值为0。
2.等级沉没(Rank Sink):如果一个网页只有出链,没有入链(如下图所示),计算的过程迭代下来,会导致这个网页的PR值为0(也就是不存在公式中的V)。
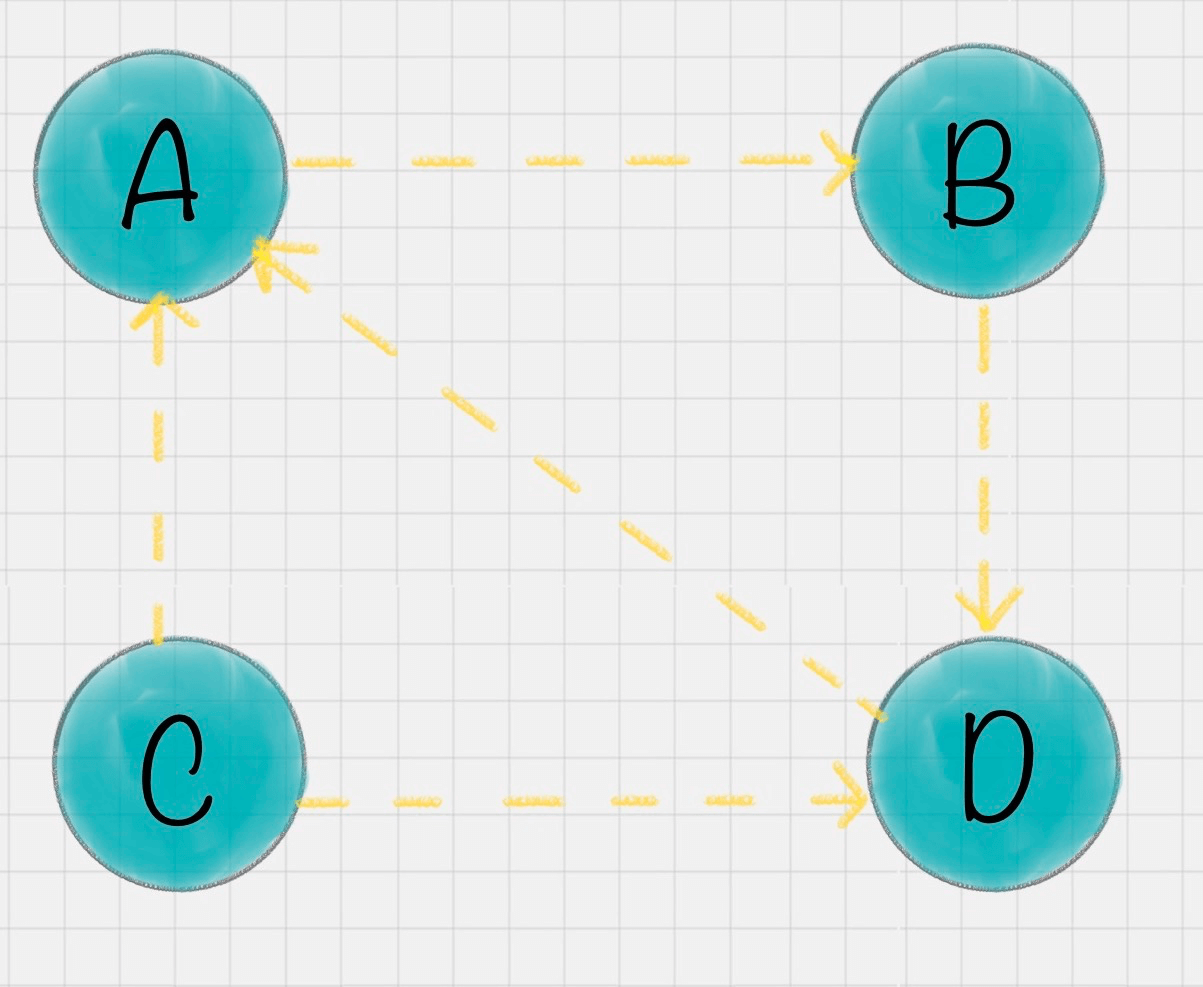
针对等级泄露和等级沉没的情况,我们需要灵活处理。
比如针对等级泄露的情况,我们可以把没有出链的节点,先从图中去掉,等计算完所有节点的PR值之后,再加上该节点进行计算。不过这种方法会导致新的等级泄露的节点的产生,所以工作量还是很大的。
有没有一种方法,可以同时解决等级泄露和等级沉没这两个问题呢?
为了解决简化模型中存在的等级泄露和等级沉没的问题,拉里·佩奇提出了PageRank的随机浏览模型。他假设了这样一个场景:用户并不都是按照跳转链接的方式来上网,还有一种可能是不论当前处于哪个页面,都有概率访问到其他任意的页面,比如说用户就是要直接输入网址访问其他页面,虽然这个概率比较小。
所以他定义了阻尼因子d,这个因子代表了用户按照跳转链接来上网的概率,通常可以取一个固定值0.85,而1-d=0.15则代表了用户不是通过跳转链接的方式来访问网页的,比如直接输入网址。
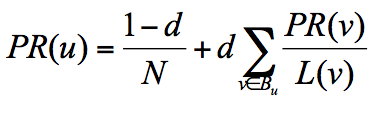
其中N为网页总数,这样我们又可以重新迭代网页的权重计算了,因为加入了阻尼因子d,一定程度上解决了等级泄露和等级沉没的问题。
通过数学定理(这里不进行讲解)也可以证明,最终PageRank随机浏览模型是可以收敛的,也就是可以得到一个稳定正常的PR值。
网页之间会形成一个网络,是我们的互联网,论文之间也存在着相互引用的关系,可以说我们所处的环境就是各种网络的集合。
只要是有网络的地方,就存在出链和入链,就会有PR权重的计算,也就可以运用我们今天讲的PageRank算法。
我们可以把PageRank算法延展到社交网络领域中。比如在微博上,如果我们想要计算某个人的影响力,该怎么做呢?
一个人的微博粉丝数并不一定等于他的实际影响力。如果按照PageRank算法,还需要看这些粉丝的质量如何。如果有很多明星或者大V关注,那么这个人的影响力一定很高。如果粉丝是通过购买僵尸粉得来的,那么即使粉丝数再多,影响力也不高。
同样,在工作场景中,比如说脉脉这个社交软件,它计算的就是个人在职场的影响力。如果你的工作关系是李开复、江南春这样的名人,那么你的职场影响力一定会很高。反之,如果你是个学生,在职场上被链入的关系比较少的话,职场影响力就会比较低。
同样,如果你想要看一个公司的经营能力,也可以看这家公司都和哪些公司有合作。如果它合作的都是世界500强企业,那么这个公司在行业内一定是领导者,如果这个公司的客户都是小客户,即使数量比较多,业内影响力也不一定大。
除非像淘宝一样,有海量的中小客户,最后大客户也会找上门来寻求合作。所以权重高的节点,往往会有一些权重同样很高的节点在进行合作。
PageRank可以说是Google搜索引擎重要的技术之一,在1998年帮助Google获得了搜索引擎的领先优势,现在PageRank已经比原来复杂很多,但它的思想依然能带给我们很多启发。
比如,如果你想要自己的媒体影响力有所提高,就尽量要混在大V圈中;如果想找到高职位的工作,就尽量结识公司高层,或者认识更多的猎头,因为猎头和很多高职位的人员都有链接关系。
同样,PageRank也可以帮我们识别链接农场。链接农场指的是网页为了链接而链接,填充了一些没有用的内容。这些页面相互链接或者指向了某一个网页,从而想要得到更高的权重。
今天我给你讲了PageRank的算法原理,对简化的PageRank模型进行了模拟。针对简化模型中存在的等级泄露和等级沉没这两个问题,PageRank的随机浏览模型引入了阻尼因子d来解决。
同样,PageRank有很广的应用领域,在许多网络结构中都有应用,比如计算一个人的微博影响力等。它也告诉我们,在社交网络中,链接的质量非常重要。

学完今天的内容,你不妨说说PageRank的算法原理?另外在现实生活中,除了我在文中举到的几个例子,你还能说一些PageRank都有哪些应用场景吗?
欢迎在评论区与我分享你的答案,也欢迎点击“请朋友读”,把这篇文章分享给你的朋友或者同事。