数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
生活中,你是不是也经常遇到这样的场景,夏天你平时都带着伞,偶尔一天没带伞,结果就正好那天下雨了;不打车时街上到处都是空出租车,但等你需要打车时发现全是满员的;别人的飞机都是正点,你坐飞机永远都是晚点(我自己就是这样)……
类似的事情还有很多,总之你越不希望某件事情发生,这件事情往往就会发生,而在发生之后,有的人就会抱怨说自己运气不好。那真是运气不好吗?这背后有什么原因吗?
其实业内我们经常称这样的“效应”为墨菲定律。今天我们就先来说说它的起源,然后再来聊聊它背后反映的数据分析知识。
1949年,美国的一位航空工程师爱德华·墨菲与美国空军共同研究高速载人火箭“雪橇MX981”,需要把16个精密传感器装在超重实验设备上测试耐压性。可即便是超重实验设备在巨大压力下都变形了,传感器也没有任何的指示。检查后才发现,原来是负责装配的三个同事把这16个传感器全都装反了。
对此,墨菲不经意间开了一个玩笑:“如果一件事情有可能出错,让他去做就一定会弄错”。随后的记者招待会上,他的上司斯塔普把这句话称为“墨菲定律”,并表述为:“如果有两种或两种以上的方式去做某件事情,而其中一种选择方式将导致灾难,则必定有人会做出这种选择。”
随后,人们对墨菲定律又做了更多诠释,比如:
那么墨菲定律背后的数学原理是什么呢?这里就要引入一个数学概念叫做期望值。
什么是期望值?期望值就是对可能出现的结果以概率为权做加权平均。举一个简单的例子,你买了一张彩票,有10%的概率中100元,40%的概率中50元,50%的概率不中。
那么期望值是 10%*100+40%*50+50%*0=30元。
这30元做什么用呢?买1张彩票或者100张彩票都看不太出来,但是如果你买10万张彩票,那么你中奖的钱很可能会接近300万,也就是30*10万。所以,这个30元的回报期望值,衡量了你在足够多的次数下,平均每一次事件的获得的数值。
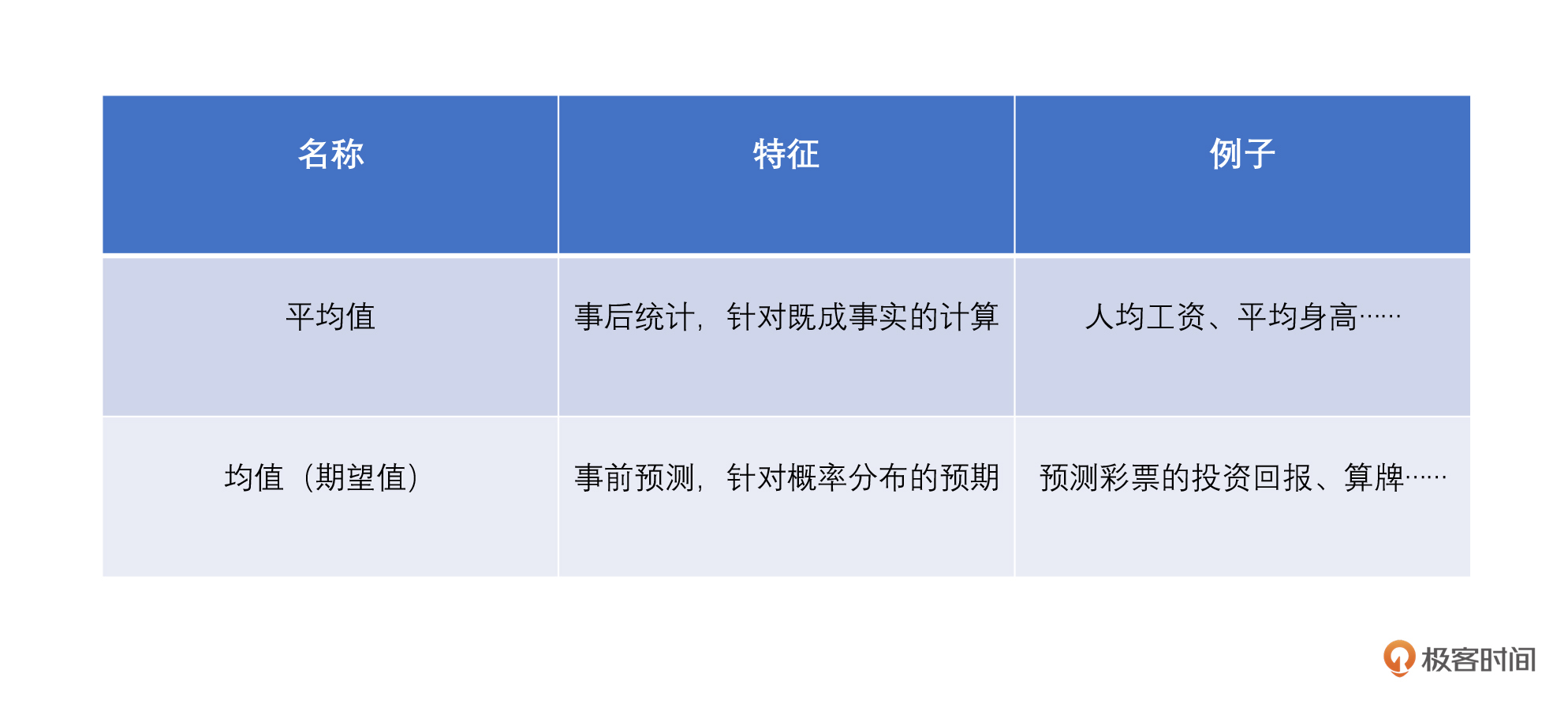
很多人在数据分析中,往往把“均值”和“平均值”混为一谈。这里我告诉你一个简单区分的方法,那就是用英文来区分:

带你了解了二者的概念区分后,我们接着来看二者的关系。我想请你先琢磨下这句话:当样本量N趋近无穷大的时候,样本的平均值无限接近数学期望(日常计算时时候相等)。这句话是不是听着很熟?对,这就是上节课我们讲到的大数定律(Law of Large Numbers,LLN)。
简单来讲,期望就是反映在大数定律下多次执行某件事情之后,得到的一个最可能的收益结果。例如,我们刚才例子用到的买了10万张彩票获利300万,平均值(Average)和期望值(或者说均值Mean)都是30元,其实就是利用了大数定律来解释这个现象。
聊完平均值、期望值(均值)和大数定律三者的关系后,我们再回到今天要用数据分析解释的现象:墨菲定律。
人都有一个特殊的心理机制,那就是倾向于记住一些不好的事情。就像航班晚点的概率对每一个人而言都是一样的,但对我来讲,每次飞机晚点的等待就会让我印象深刻,而平时没有晚点的时候,我的注意力都集中在其他事情上。
现在,我们可以把坏事情的期望定义成M,它代表着你记住这个坏事情的概率,坏事情的心理影响定义成X,概率为R1;再把好事情的期望定义成N,它代表着记住这个好事情的概率,好事情的心理影响定义成Y,概率为R2。根据今天所学,我们就有了如下两个公式。
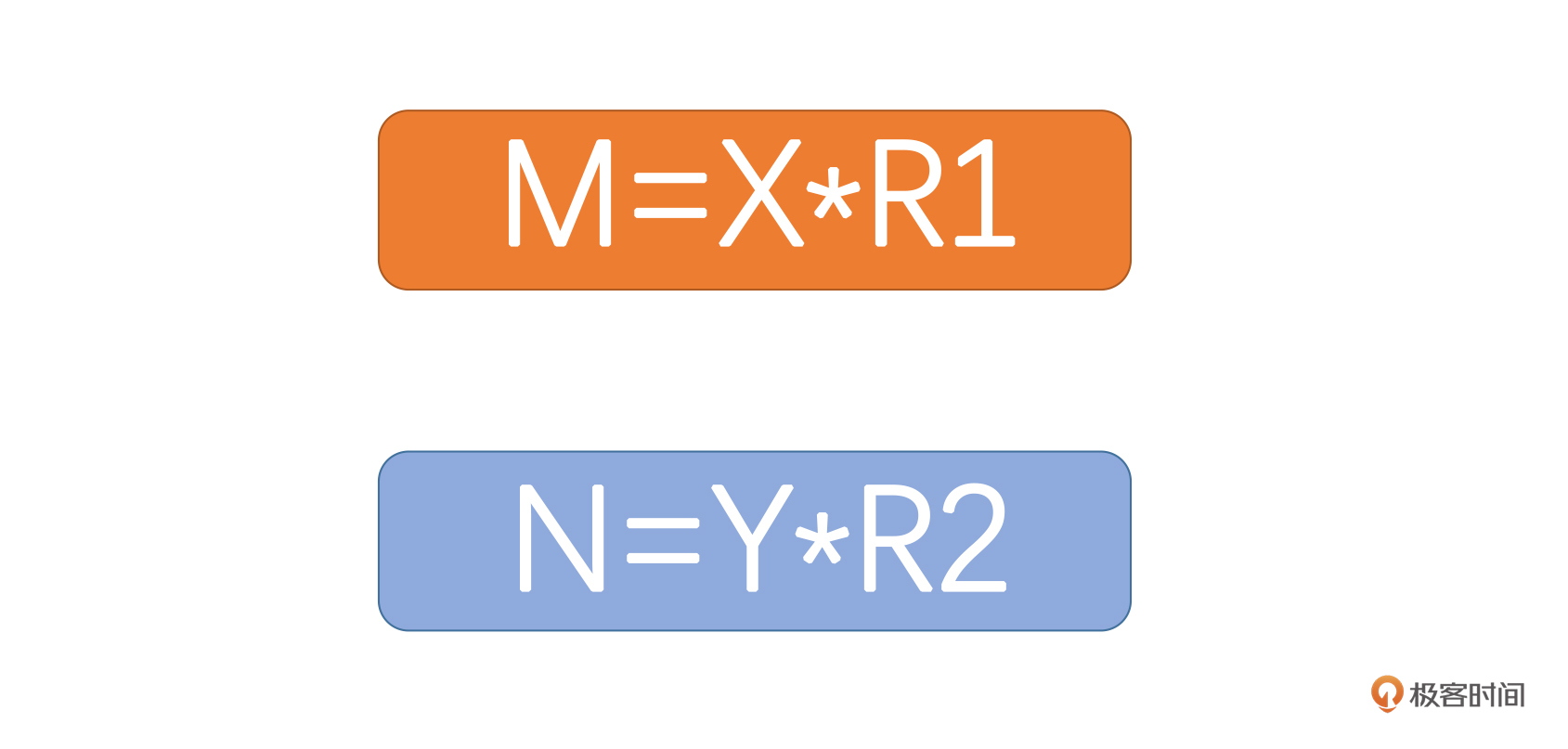
抽象一下,你经常担心一个坏事的发生,比如说事情A,我们假设A发生时对你产生的心理作用是X,事情A不发生对你产生的心理作用是Y。这个时候显然X是大于Y的,所以当发生A这件事情的时候,你受到的心理影响X就比Y大。
其实,你在担心一件事情的发生之时,这件事情已经具备了发生的大多数条件。我们假设事件A发生的概率是R,那么当你担心这件事情发生(R1)和不担心这件事情发生(R2)的时候,两个概率是不一样的,R1一定大于R2。
这样一来,把我们的讨论代入前面的公式,一个我们担心的坏事的发生期望就像下面这个图所显示一样,对比一下你就会发现,墨菲定律的原理其实是由我们对于好事情和坏事情的期望值差异造成的。简单讲,印象深刻再加上担心的时候概率高,自然也就担心什么发生什么了。

我们现在用墨菲定律来解释一下这节课开头的情景:
于是,墨菲定律就产生了。
了解了墨菲定律的成因后,你是不是想问,那我们怎么才能避免掉入“墨菲定律”的陷阱呢?
其实影响期望的变量分为两个部分,分别是心理影响大小以及发生概率大小,所以我们可以从这两个方面入手。
对于心理影响来说,我们要做的就是不断调整事情对你心里影响的预期,让它们趋同。特别是遇到坏事情的时候,你可以通过增加B计划等方式,调整预期以降低坏事情发生对你的心理影响。
对风险的概率来说,你可以优化流程,提高自身能力,尽可能减少事件出错的概率。
这么说可能还是有些抽象,我们来看几个工作与生活中的运用。
“为大概率坚持,为小概率备份”——创业的时候,我们要努力为好的期望(N)去坚持,同时考虑为坏的影响(X)备份,应该尽力降低坏期望(R1)的风险。
“已知的是成本,未知的才是风险”——如果坏的影响(X)为已知,那么即使你按照坏事件发生概率(R1)100%来准备资金,这批资金也算是你付出的成本;但如果坏影响(X)未知,那么无论坏事件发生概率(R1)为多少,都是风险,因为你不知道这个坏事件究竟会造成多大的影响。
“项目风险控制”——项目管理当中有各种风险管理和预防措施,把风险分为很多类,例如静态风险、动态风险、局部风险、整体风险,同时也会把风险应对措施细分为很多类,其实背后的核心是为了去避免墨菲定律的发生,让整体项目在项目经理的期望值下正确运行。
“生活中的风险控制”——我们在生活中,其实也是可以借用这种风险控制的方法论,识别生活中的风险并做好准备,这样才能够在墨菲定律发生的时候不会手忙脚乱。例如提前看看天气预报,查看这趟航班的过往准点率,预估自己乘坐航班情况。在去重要会议的时候,多提前一些时间。这些生活里的小事你或许平时不会太过于在意,但请相信,一旦你把这些小事落到实处,你对生活的掌控力会大大提升。
数据分析解释给你的是现实背后的规律,学以致用才可以让它们发挥最大的价值。
好,总结一下,今天我们通过墨菲定律给你介绍了一个有意思的概念叫期望值(Mean),它是对可能出现的结果的概率加权平均,期望值完全是由概率分布决定。而我们之前讲的平均值一般是指算数平均值,也就是一组数据中所有数据之和再除以数据的个数。某个事情长期不断发生,次数足够多后会达到我们预设的期望值,这就是大数定律。
这几个概念相互依存,又相互不同。其实你可以把平均值、大数定律和期望值这三节课看成一个小整体,对照进行学习。
对平均值来说,你要学会为不同事物去分组,用更细分的数据来看待问题。对于大数定律来说,要成事,其实需要我们不要有赌徒心态,要学会持续投入。而对于期望值来说,平衡预期和未雨绸缪这两个词,希望你能够在生活中灵活运用。
其实,这几个数据分析的概念都告诉我们一个最朴实的道理:没有事情可以一蹴而就(平均值),我们需要努力足够多的次数(大数定律),学会规避风险(期望值)。这样最终在若干年后,企业和个人才能有一份满意的企业/个人数据报表。
数据给一双看透本质的眼睛,调整好自己的期望,持续学习持续进步。
今天我们把平均值、大数定律和期望值给你串讲了一下,你最近在生活中遇到过墨菲定律的事情么?你觉得怎么做可以减轻和规避这些风险?希望你分享在留言区,我们一起共同成长。
另外,如果你对墨菲定律还有一些其他的认知,也可以写在留言区,我们一块讨论。感谢阅读,如果你觉得这篇文章对你有帮助的话,也欢迎把它分享给更多的朋友。
评论