
数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
今天我们来聊聊数据抽样。无论在小数据时代还是大数据时代里,数据抽样都是非常常见的数据分析手段。人口普查、调查问卷、人工智能训练的过采样等等都是抽样的方式。我们之前学到的随机对照分布、直方图,散点图等等内容,它们数据的来源其实大部分也都是来自抽样数据形成的数据。
用好了数据抽样,你就不必大费周章去拿到每一个人的数据,可以“四两拨千斤”,在非常复杂的数据环境里面找到合适的数据结论。所以我把数据抽样称作数据分析方法的“涡轮加速器”,用好它你可以快速地收集到你想要的数据,从而更好地指导你的工作和生活。
数据抽样其实可以分成小数据抽样和大数据抽样,我们先从最常见的小数据抽样入手。小数据抽样有4种比较常见的方式,它们分别是简单随机抽样、系统抽样、分层抽样和整群抽样。为了便于你理解,我把这四种抽样放在一个情景下来给你讲解。
大情景是这样子的:印度的新冠肺炎疫情现在很严重,我们想知道大概印度新冠肺炎疫情发病率是多少。

这件事情我们该怎么做呢?让所有印度人都做一遍新冠测试是不太可能的,我们只能选取其中一小部分人来做测试。具体涉及选哪部分人的问题上,我们可以有四种不同的方式去选择:
简单随机抽样:我们设印度总人口是N,我们可以在印度大街上,随机地抽取 m个访问对象来去做检测(m的数值可以根据前面的算法模型来进行确定)。最后根据这m个对象的测试结果,再根据前面的算法模型推算出整体印度新冠患病率。
抽象一下,简单随机抽样就是从总体N个单位中随机地抽取m个单位作为样本,使得每一个样本被抽中的概率相同。这种抽样的特点在于每个样本单位被抽中的概率相等,每个样本单位完全独立,彼此间没有关联性和排斥性。
但是简单随机抽样这种方法有一些执行层面的问题。比如在印度大街上很有可能具体执行的时候,调查人员图方便,仅仅在某几个街区来做调查。然后这几个街区恰好不具有全局的代表性,数据偏差的问题就随之出现了。
针对这种偏差,有一种抽样方法改善了简单随机抽样里执行步骤的规则,它就是系统抽样。
系统抽样:为了避免调查人员全都扎堆到某几个地区去做抽样,我们可以立下一个规则,让每一个街区只能有10个人进行调查,并且街区和街区之间不得少于10公里。这样的话,在执行上就会更加容易,也能够更好地确保数据的随机性。
把上面的这个方法再抽象一下,系统抽样方法就是依据一定的抽样距离,从整体中抽取样本。这样做的好处是比较简单而且不容易出错,组装工厂里对手机质量进行抽样检测用的就是这个方法。
系统抽样解决了在随机抽样执行过程中无法真正随机的问题。但是这个方法依然有缺点,比如我们即使在每个街区上去找人抽样,你会发现在印度外出的男人比较多,而且大部分都是成年人。孩子、老人和妇女可能都在家中,这样随机抽样的结果其实也不能够完全代表全部人员患新冠的比例。
这个时候为了保证我们拿到的是全印度人民的新冠患病比例,我们就会再用下面这种分层抽样的方式来确保整体的样本是均匀分布的。
分层抽样:我们在系统抽样的结果之上可以再加一个人口分层,根据年龄、性别、地区这样的规划分成不同的层。随后我们在每一个细分的层里面,再去随机地抽取样本进行测试。这样的结果会更接近最终的事实,但是它的执行的复杂性也更高了。
我们再把分层抽样来抽象一下,分层抽样就是将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本,从而保证样本的结构接近于总体的结构,提高估计的精度。
这里特别要说的是,在为了避免“辛普森悖论”的时候,我们通常把不同维度的人群都抽样一部分进行计算。
用了分层抽样这个方法,的确统计精度更高了,但是问题又来了:分层抽样的可执行性太差了,根本没法在印度当地细分出这么多的层,然后再让调查人员去分不同年龄段、不同地区、不同性别分别统计。
整群抽样:针对在印度没法细分这么多层的情况,我们得把刚才的这些层合并起来形成一些大组,然后针对这些大组进行抽样。这种方法叫做整群抽样,在企业单位进行人力调查反馈的时候经常会用到。
抽象一下,整群抽样就是将总体中若干个单位合并为组(这样的组被称为群),抽样时直接抽取群,然后对所选群中的所有单位实施调查。抽样时只需要群的抽样框,可以简化工作量。你会不会觉得分层抽样和整群抽样不太好区分?告诉你一个分辨小技巧:分层抽样是先分层再从各层抽样本,整群抽样是先分群再抽一个群调查。
整群抽样方法也有很明显的缺点,那就是精度较差,很可能出现一些偏颇的情况。所以如果你发现你在员工调查问卷里被贴了一些不切实际的标签,也不用感到特别奇怪——因为整群抽样不是那么精确。
所以你学到这可能会有点懵,这四种抽样方法都各有优劣,那么我们在日常使用过程中,应该如何选择呢?
给你讲完了小数据抽样后,我们现在把目光放到大数据抽样。大数据抽样是现在科技界的热门话题,不知道你有没有读过维克托·迈尔·舍恩伯格的《大数据时代》呢?如果没有的话,我推荐你学完这节课后去读一读。
舍恩伯格提出的三种大数据时代的思维变革:要全体不要抽样、要效率不要绝对精确、要相关不要因果。这三种思维变革被大多数人所接受,大数据也被很多人冠以数据抽样终结者的称号。
这种观点和我现在要讲的大数据下如何去做数据抽样格格不入,所以我要先花一点时间讲清楚为什么大数据时代还需要抽样这个问题。
大数据时代为什么还需要抽样呢?我来给你讲讲三个主要原因,你也可以自己思考一下。
首先从数据分析目标上讲,大数据之所以是大数据,是因为可以分析到每个人的行为,从而进行计算和推荐。如果我们针对的是千人千面的个性化推荐,那一定是将每个人的数据进行分别存储和计算的,否则就失去了大数据的意义。而针对数据的统计分析和BI分析指标,还是可以复用原先的数据分析方法和抽样原则。因为大数据也没有逃脱数学的法则,在允许一定误差的情况下,抽样可以大幅缩减参与计算的数据量,这和舍恩伯格提到的“要效率不要绝对精确”是一致的。所以在大数据下的统计分析可以沿用小数据的抽样算法,这一点是具有理论基础的。
其次,在做数据分析的时候,对数据质量的要求是要远远大于数据量的,所以数据并不是越多越好。而抽样过程能帮助我们控制有效数据的比重,我们可以用各种各样的规则去做数据处理,而不是不假思索地将所有数据都纳入其中,否则一个看似从大数据里找到的规律,很可能只是一个计算口径或者数据质量的问题。因此大数据也要了解数据的构成,也可以进行合理的抽样。
最后,从数据量级来看,每年的数据量级都以指数级增长,当IoT数据时代来临后更是爆炸式增长。数据的迅速增长对于普通公司甚至于大型公司来讲都并不全是好事,以大数据全量计算一些需要实时反馈结果的数据分析任务也是不划算的。毕竟每一次全量计算动辄1个小时,多则1天,这会非常影响数据分析师的分析思路。我们期待的数据分析是可以数秒内反馈的,这样能提高数据分析师的分析效率,合理的抽样方法可以有效提升计算效率。
上次遇到舍恩伯格时,我问了他类似的问题。他给我的回答是:“大数据并不是否定统计学,大数据是一个综合了统计学、工程学、人工智能等的综合学科,扩展了这些学科的边界。”我想这也是对这个问题的正式回应,大数据并不是否定原有的统计学原理,而是用工程能力扩展了统计学和数学。
回到舍恩伯格这句话,“要全体不要抽样”,舍恩伯格其实针对的是因为大数据采用了更大的计算能力,可以对每一个个体进行分析和统计,然后采取相关行动(例如对推荐来说,你在抖音里每个视频都是针对你个人的一个推荐)。指的是全体当中个体,他说是针对每一个人都有特殊的解决方案,而不是抽样某几个人就把针对这几个人的解决方案给全体人员。
对于过去统计学涉及的整体统计指标、趋势分析、分布分析这些知识来说,依然可以使用抽样的方式来解决整体人群的趋势问题。所以,舍恩伯格没错,我说的也没有问题,这只是针对大数据的两个不同的分析场景而已。
现在你知道了,在大数据分析中,我们也经常会用到统计学的抽样方法。在大数据环境下,抽样统计方法会有什么不同呢?我举两个常用的在大数据情况下使用的抽样算法给你讲解一下。
在大数据环境下抽样最典型的就是一个叫蓄水池的抽样算法。它非常有名,甚至被写入到全球领先的大数据公司Cloudera公司数据平台的 Clouder ML中,成为常用函数。同时,它也是硅谷面试数据工程师时最流行的面试题。
那蓄水池算法指的是什么呢?它说的是这么个问题:“给你一个长度很大或者长度大小未知的数据(流),并且你只能访问一次该数据(流)的数据。请写出一个随机选择算法,使得选中数据流中每个数据的概率都相等。”
对于文科生听上去有点是天书,我用大白话再给你翻译一下。
还是用刚才印度新冠肺炎疫情这个例子,假设印度现在人太多,没人知道印度有多少人口,也不知道印度的整体情况是什么,我们要去通过抽样调查统计新冠的比率,我只能遇到一个人去统计一个人,然后要有个算法看是不是抽中这个人来调察。但是怎么能够让每个人被选中的概率相等呢?
这时蓄水池算法应运而生,我给你简单分享一下它的算法思路。我们需要把抽中做统计的印度人都放到一个游泳池(蓄水池)里。假设我目标是只抽n个人,这就有一个有n个人容量的游泳池,抽中的人都站在这个游泳池里面。当游泳池站满了以后,再往里加人的话有一定的概率会把游泳池里面的人给挤出来,也有一定的概率是新加的人根本挤不进去游泳池(想象一下上班时间的北京地铁)。
这样无论一共有多少人进来,他都有一定概率挤进游泳池里或者被挤出去,游泳池里面最后留下来的人,就是我们要的随机的n个人,这些就是我们的抽样结果。我们最后统计这些人的新冠阳性情况时,就可以说我们是随机抽样的,而不用管印度一共有多少人口了。
这就是大数据下的蓄水池抽样算法,详细的推导我放在了这节课的附录,你如果感兴趣可以去附录里进一步学习。通过这个硅谷最热门的面试算法题,你就知道了:大数据计算时也是经常会抽样的。
大数据里因为数据非常多,所以往往某一类的数据远高于另一类数据,而这些数据都直接给我们下一章讲到的人工智能算法的话,我们造出来的人工智能可能就学坏、学歪了,因为人工智能就像一个小孩子,你教给它什么,它就学什么,你天天告诉它麻子脸的人是美女的话,将来它的审美就是如此。
所以在大数据里,除了刚才提到的蓄水池抽样算法之外,还经常会遇到两种抽样方法:过采样和欠采样。过采样就是在一个池子里反复去抽样,本来应该抽样10个人,我们把这10个人反复抽样,变成50个人。欠采样就是在一个池子里本来我们应该抽样100个人,现在只抽样10个人。
举个例子,我们现在想训练我们的人工智能去分辨什么是美女。这件事情可挺难的,因为世界上的美女比较少,长相比较普通的女生比较多。如果我们给人工智能真实世界里边的女生样本去训练,他可能就认不出来哪些是美女了。因为美女太少,它学的不够。
在这种情况下,我们就会采用“过采样”的方式,将美女的数据复制为多个以供人工智能去学习;而对于普通女生,我们就可以采用“欠采样”的方式,保持两者数据量的平衡。这样在人工智能这个小孩看来,世界都是1:1的,他更容易去区分美和丑,就像下面这个图的样子。
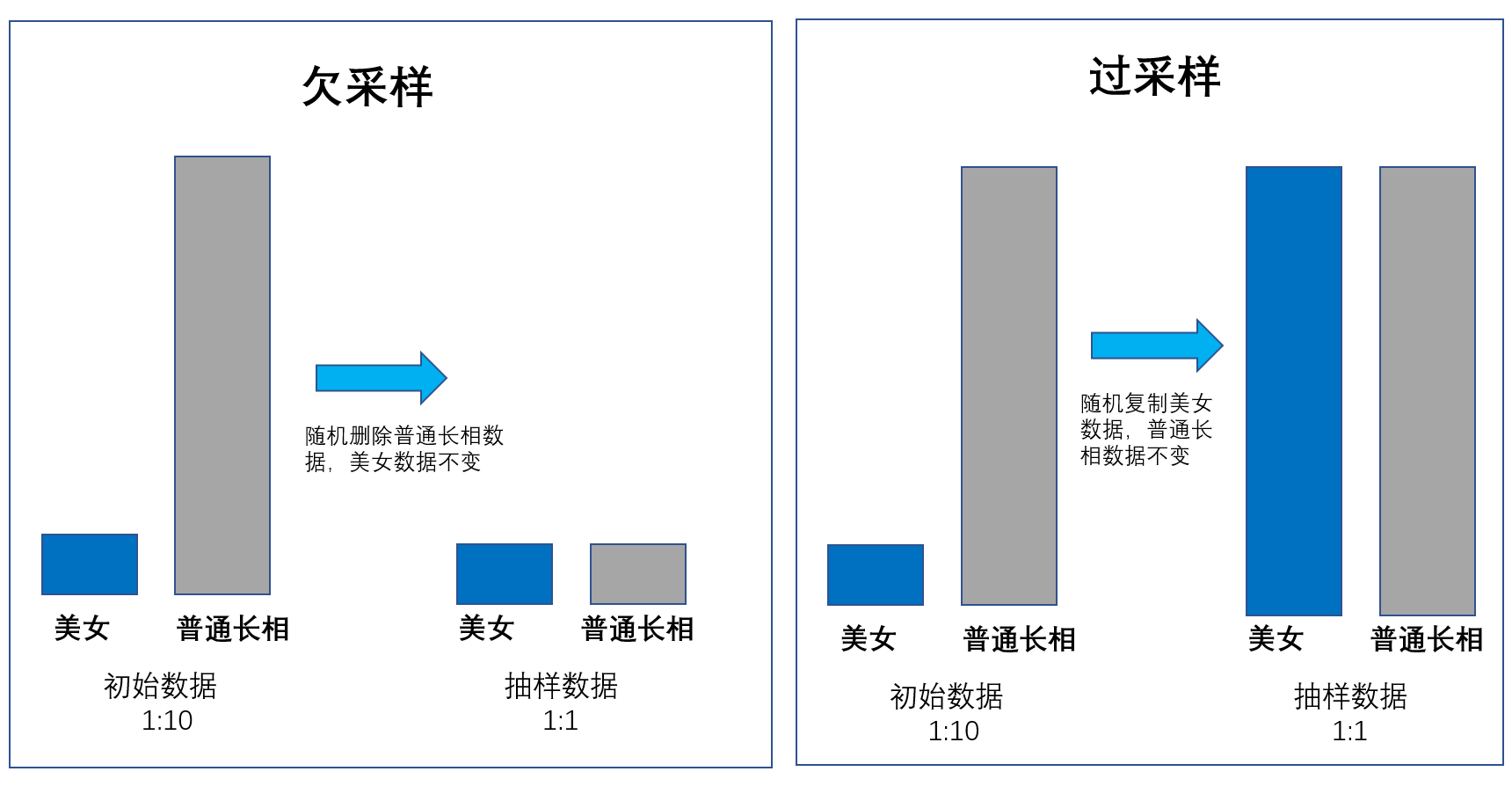
所以,抽样其实在大数据计算当中是普遍存在的,特别是一些大数据计算高手或者数据科学家都会娴熟地利用各种抽样方法,事半功倍地解决大数据分析问题。由此可见,前面提到的“大数据是数据抽样终结者”的传言,基本上是不明真相的吃瓜群众杜撰出来的。
好了,这节课到这里也就接近尾声了,我们再来总结一下。这节课首先给你讲了数据抽样的概念,通过一个统计印度新冠肺炎疫情的例子,给你讲了小数据抽样里最常见的四种方法:简单随机抽样、系统抽样、分层抽样和整群抽样。
然后我们讨论了“大数据是否需要抽样”这个问题,我给出的答案是需要。主要有以下三个原因:
最后我们还聊了聊大数据中的抽样算法:蓄水池算法(当然我给你讲的是游泳池算法)、过采样、欠采样。通过这节课的讲述,我想让你明白一个道理:大数据其实不是数据抽样的终结者,无论是大数据还是小数据,它都无法逃离统计学、数学、集合论、数据结构等这些基础理论的约束。所以我之前给你讲的数据分析的原理,也同样适用于大数据环境。
如果你能把数据抽样的这个“涡轮加速器”运用到你自己的工作和生活当中,那么你就可以事半而功倍,通过针对一小部分的人和事情的观察而看到整个事物的整体情况。古人说“管中窥豹,可见一斑”,那么对应到我们的数据分析上,说的就是合适的数据抽样算法能够由点及面地看到事物的全貌。
数据给你一双看透本质的眼睛。希望你能通过抽样算法,事半功倍地解决你工作和生活当中的问题。数据知识学无止境,让我们一起持续学习,一起共勉。
你在日常生活当中有运用过抽样的方法吗?如果有,你具体是如何运用抽样的方法来解决你工作与生活的问题的?希望你分享出来,给我们大家一起开拓下眼界!
1.将1~n条数据,存入待定长为n的集合序列,从这个序列里随机抽取k条数据,每条被抽取的概率为:k/n。
2.读到于第k条数据时:
整体证明这个算法是公平的过程,你可以参考知乎的这篇文章。
单机版本实现起来可以如下实现,直接调用Sampling(k),就可以得到蓄水池中的k个数据。
public class ReservoirSampling {
private int[] ALL; // 整体的水池中的数据
private final int N = 100000; // 整体数据规模
private final int K = 1000; // 水池规模
private Random random = new Random();
public void setUp() throws Exception {
ALL = new int[N];
for (int i = 0; i < N; i++) {
ALL[i] = i;
}
}
private int[] Sampling(int K) {
int[] Pool = new int[K];
for (int i = 0; i < K; i++) { // 前面K个印度人直接进入水池
Pool[i] = ALL[i];
}
for (int i = K; i < N; i++) { // K + 1个元素开始进行概率采样
int r = random.nextInt(i + 1); //这就是K/N的概率
if (r < K) {
Pool[r] = ALL[i]; //如果被选中了,那么这个人就被从蓄水池中挤出来,用新人进去
}
}
return Pool;
}
}
评论