数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
在散点图那节课里,我们其实留下了一个问题:我们想找一个趋势线把这个散点图的趋势画出来,那么趋势线我们怎么才可以找到呢?最常见的做法就是用我们今天要讲的回归算法。
回归(Regression)是由英国生物学家弗朗西斯·高尔顿(FrancisGalton)提出来的。简单来讲,回归就是研究一个变量和另外一个变量的变化关系。其中一个变量我们叫做因变量,另外一个叫做自变量。多元的回归,就是研究一个因变量和多个自变量之间的关系。
一般来说,当我们知道了某一种情况或现象,想要去了解这个结果和前面哪些因素发生了怎样的关系(例如体重和年龄的关系),或者想验证某一些数据其实和结果没关系,这个时候我们就可以用回归验证。当我们知道了过去的一些数据情况,我们想根据以前的经验值,预测将来可能出现的结果,这个时候我们也可以用回归分析和相关的算法。
根据回归使用的场景不同,我们可以把它分成线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索回归等等。这些回归的整体逻辑比较类似,今天我给你重点介绍最常用的三种回归算法。
第一类是线性回归。线性回归里最简单的一种就是一元线性回归,它有两个变量,一个叫做因变量(Y),一个叫做自变量(X)。我们可以用 Y=a+bX 这个公式来拟合一元线性回归方程。

例如我们要计算体重和年龄之间的回归关系,这里的年龄就是自变量X,体重就是因变量Y。
这里需要注意的是,判断两个变量是不是线性关系这是从业务上面去判断的。如果我们从业务上看是多元回归的话,我们的目标是要最少的自变量,也就是找到影响结果最核心的几个因素来生成这个公式,抓到影响一个事物的关键点。
同时线性回归对异常值影响非常敏感,往往一个异常值就把一个预测带歪了。所以我们在做分析的时候,经常会先通过聚类或者后续其他算法剔除这些异常点。当然,很多时候你并不确定这些点到底是异常值还是实际数据的规律,所以你需要非常有经验的数据分析师和算法专家来参与。
学到后面你就会发现,数据挖掘难的不是算法,而是准确去掉异常点、找到影响因子这些算法之前的数据准备工作。
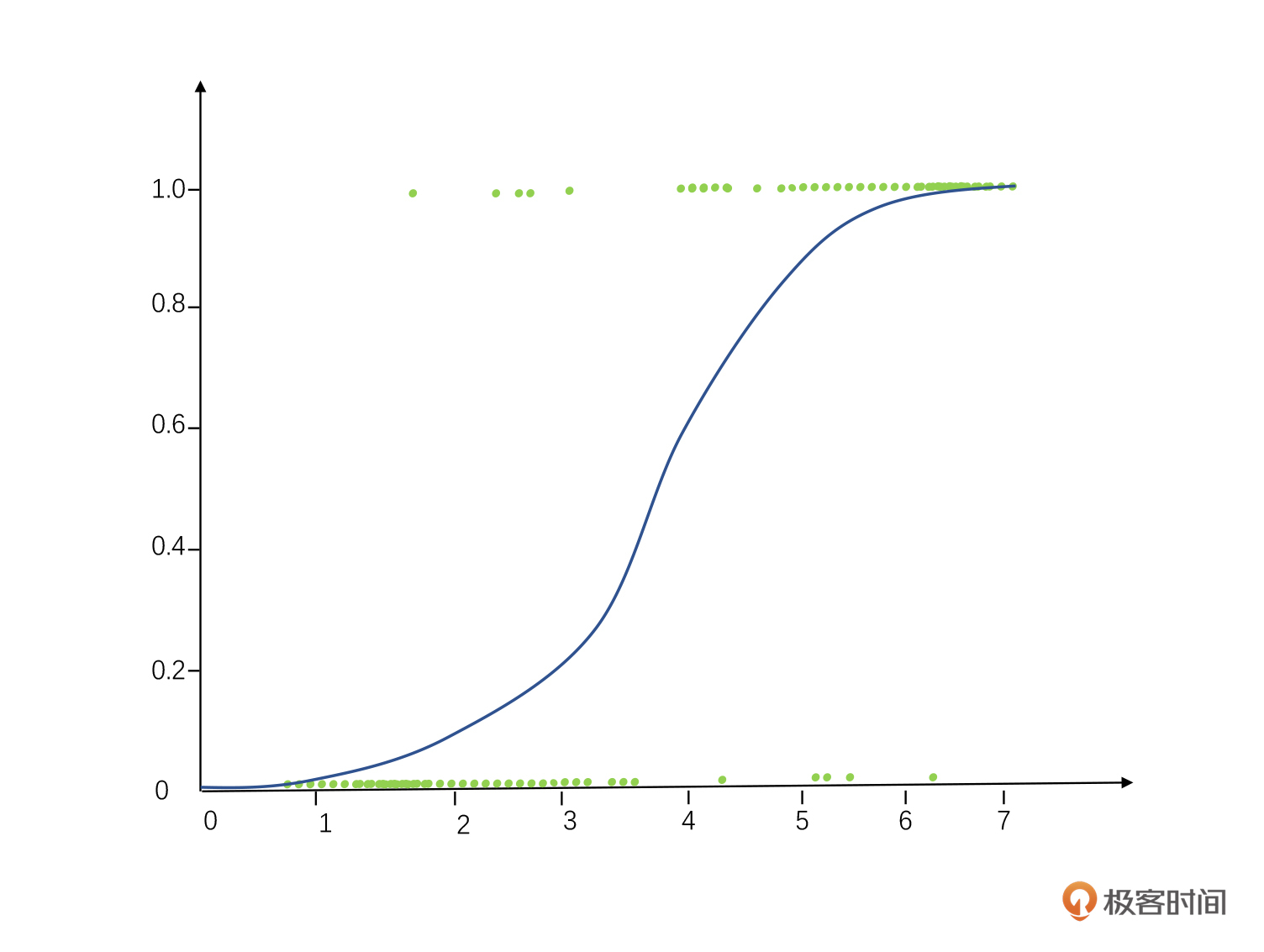
第二类是逻辑回归。逻辑回归被广泛用于做分类问题,也就是把“成功/失败”“哪一种颜色”这类问题变成线性回归的样子。基本逻辑就是把离散的因变量Y变成了一个连续值,然后再做回归。
怎么把离散的Y值变成连续的Y值呢?这里我们把事件发生的概率比上事件不发生的概率,取Log值,这样做就把一个非连续的数据变成连续数据了,具体公式如下。
Logit(Y)=Log (Odds Y)=Log((Probability of Y event)/(Probability of no Y event))
这个变化我们也叫做Logit变化,然后再通过各种各样的线性回归或者分类算法,我们可以找到对应关系,就像下图这样。
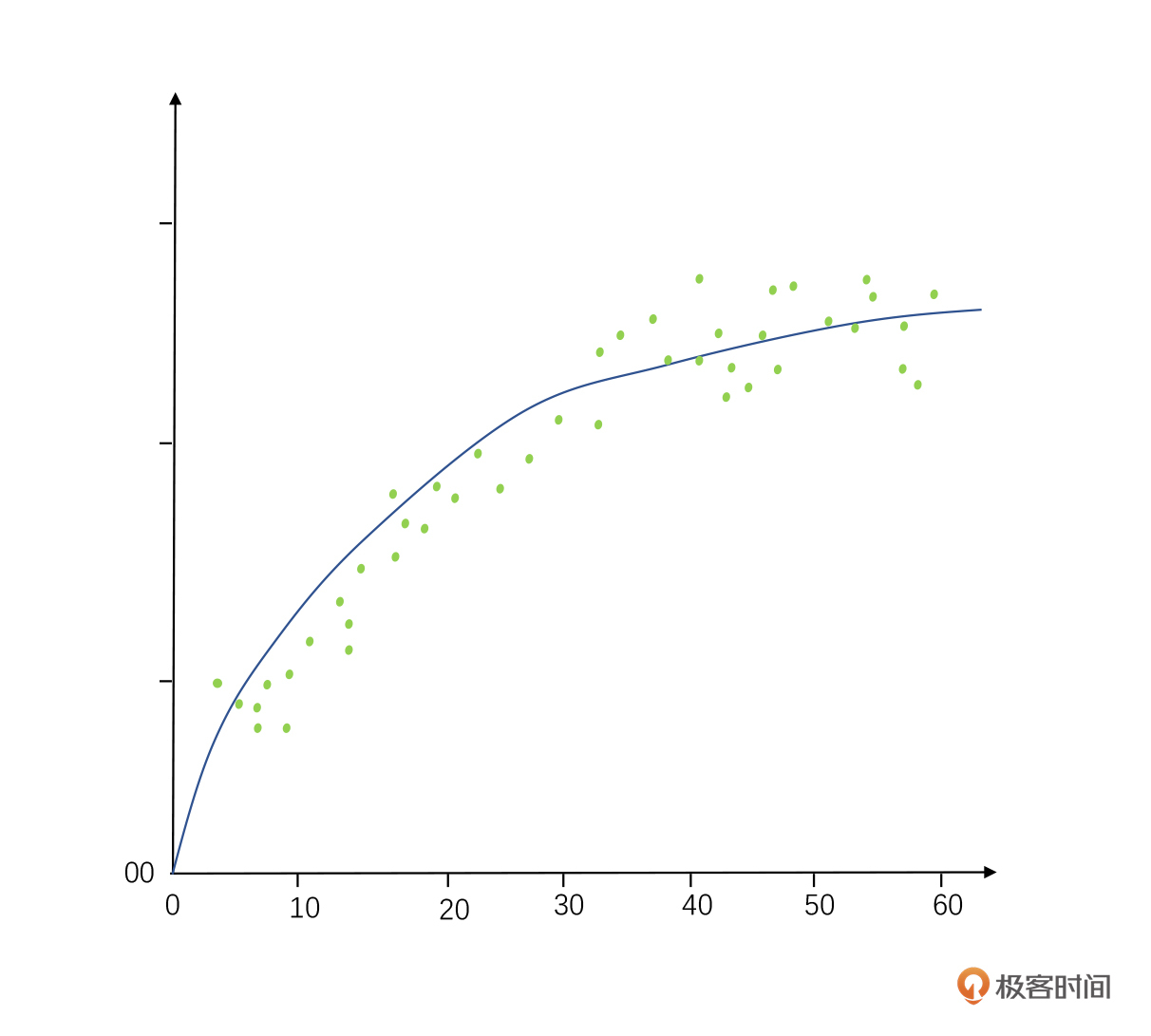
第三类是多项式回归。顾名思义,它可能出现多个指数的数据,这种回归最佳拟合的线也不是直线,很可能是一个曲线。比如我们预测人类身高增长速度和年龄的关系,最终回归出来的曲线方程可能由多次项组成,就像下图这样是一条抛物线(我们在婴儿时成长最快,岁数越大增长速度越慢)。
在使用这种多项式回归的时候,最常见出现的问题就是过拟合和欠拟合。这在将来做任何预测算法的时候都会遇到,这里先给你着重讲一下。
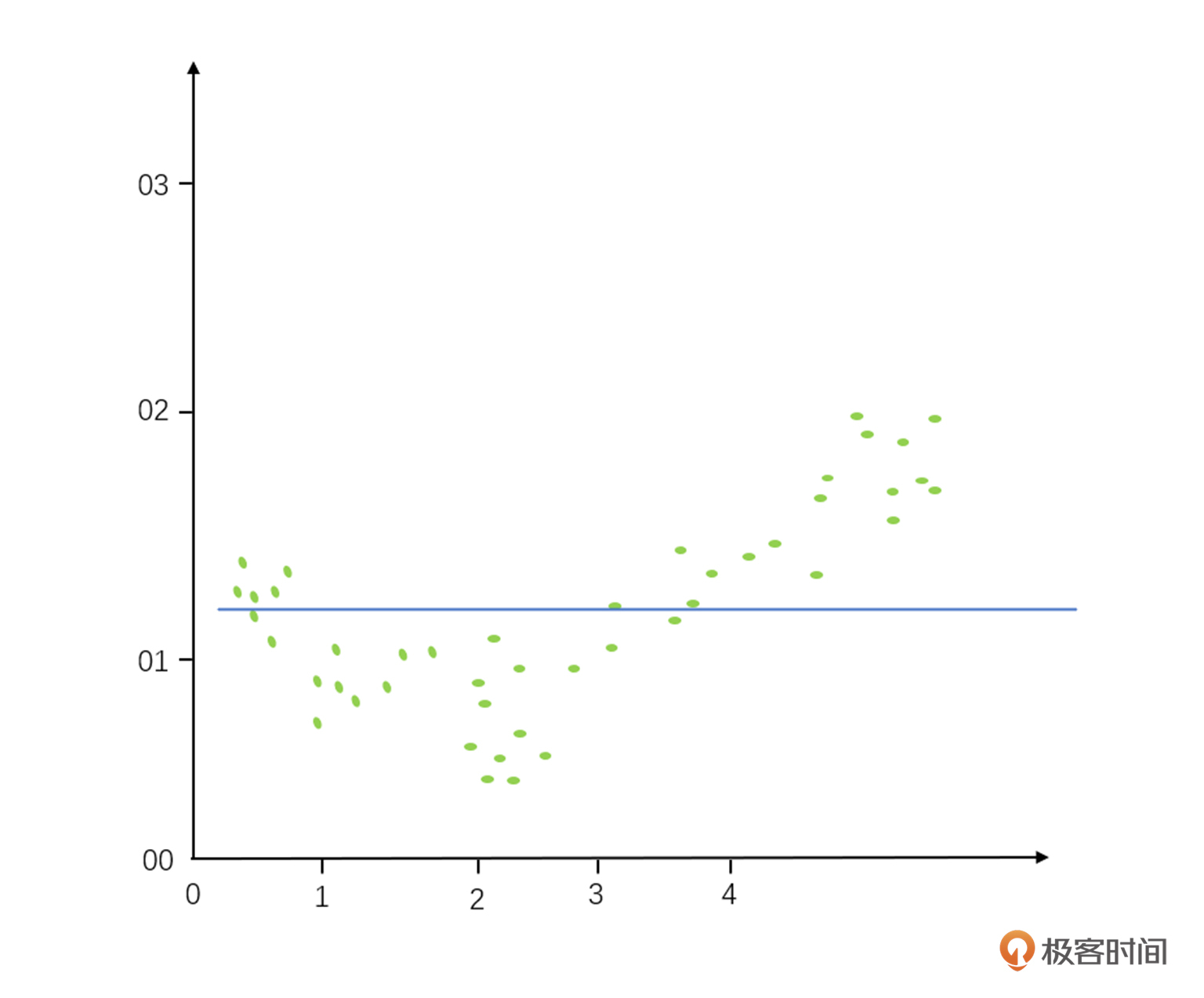
这两个概念是什么意思呢?假设我们找到一些数据画在了散点图上,我们实际背后蕴含的数据画出来之后它就像个对勾(如下图所示),是实际背后数据规律的正确答案(我们也把这个公式叫做算法模型)。
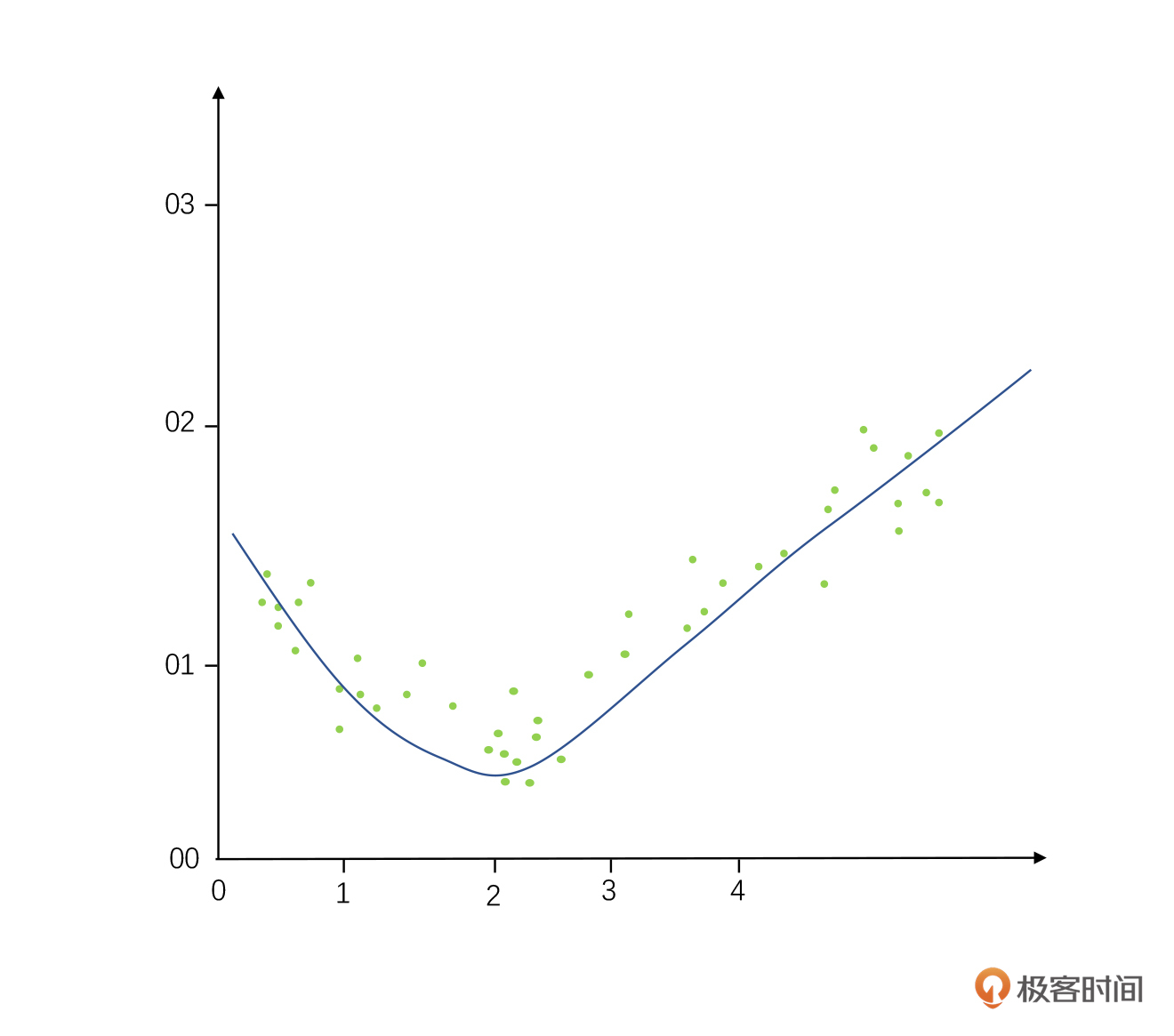
而欠拟合是画这个线(也就是推算这个公式)的时候,我们把很多细节给忽略掉了,直接画成了一根直线的线性回归,有很多趋势都没有很好地反馈出来。因为细节丢得实在是太多了,所以我们把它叫做欠拟合,这个名字意味着需要更复杂的多项式回归,才可以更准确地描述这个规律。
而过拟合是指我们太纠结于其中的细节,以至于这个数据模型计算出来的曲线变成了一条特别曲折的线(本来应该是一个相对光滑的对钩)。这样的数据模型适配性很差,换句话讲,它的查全率不高,用它做预测很可能就会指鹿不为鹿了。这就是过拟合的结果。
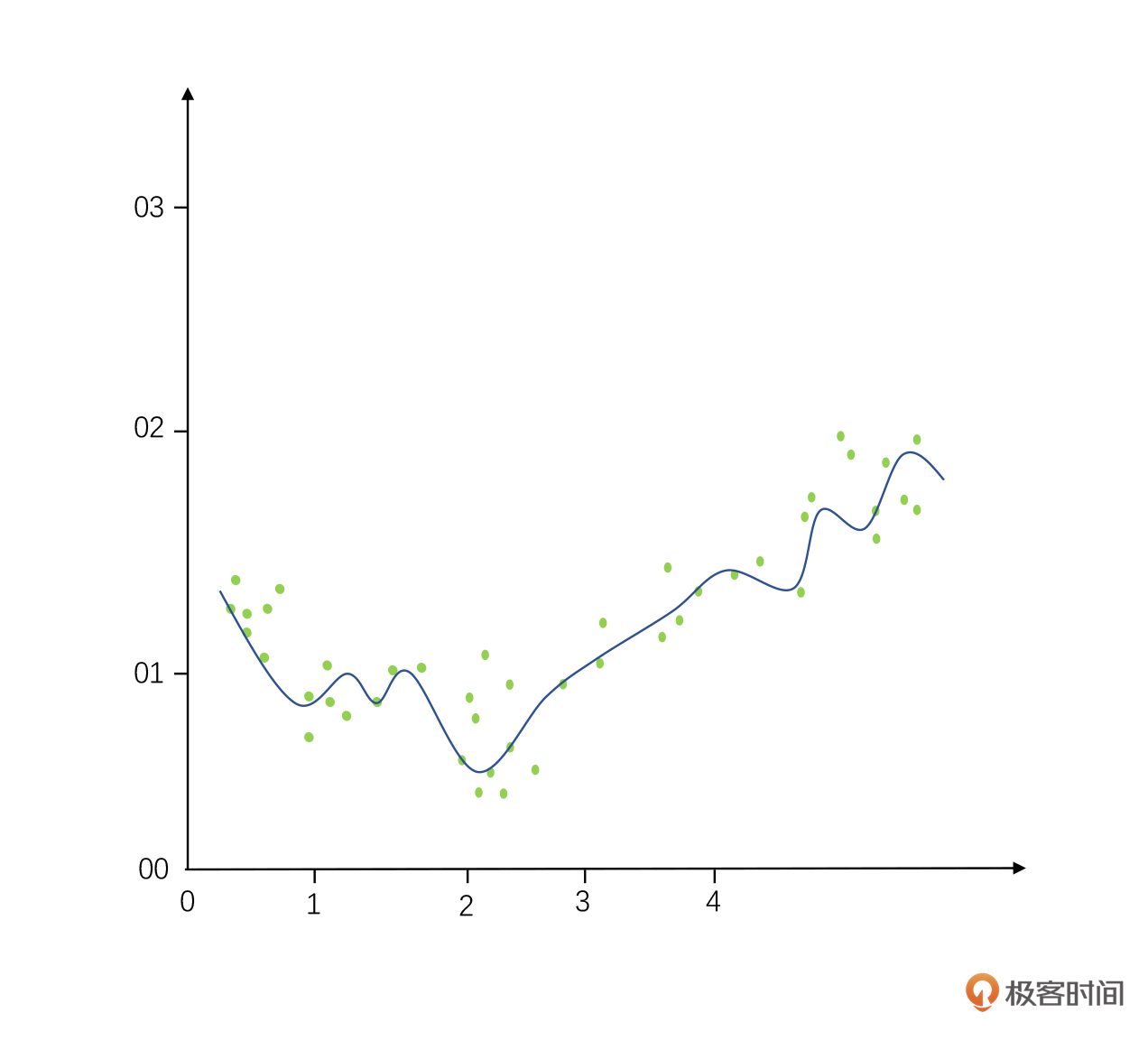
权衡是过拟合还是欠拟合的情况需要根据实际业务情况来做选择,不是光看数据就可以解决的。
有了这个回归公式以后,是不是就代表着因变量就是因为自变量的变化而导致的呢?换句话讲,自变量和因变量是不是存在因果关系?前面因果倒置那节课你学过,其实我们还不能下这样的定论。
计算出这个数据模型,我们只能够推断出一个变量对另一个变量有依赖关系,但并不代表他们之间就会有因果关系,因果关系的确立必须是来自统计之外的一些业务依据。因果这个话题你要是记不清了,可以去11讲里再复习一下。记住,两个变量之间有回归逻辑,不代表着两个变量之间有因果逻辑。
我们通过各种计算得到了回归模型之后,就可以在工作和生活当中利用这个公式很好地预测出未来的结果吗?答案是否定的,现实生活不一定有我们在算法当中预测得那么好。这就是我们接下来要讲的话题:均值回归。
谈到回归,我拿我们非常熟悉的身高来给你举个例子。根据达尔文进化论,子代会越来越基于父代进行进化。也就是说理论上父母越高,孩子也会越来越高。而一般高个子的女孩子只会找比自己身高更高的男生结婚,生的孩子也应该更高。
以此类推,理论上经过千百年的进化,人类应该分成巨人族和矮人族才对。但我们都知道现实情况其实不是这样的,人类并没有分成巨人族和矮人族,高尔顿在实验中也发现了这一点。
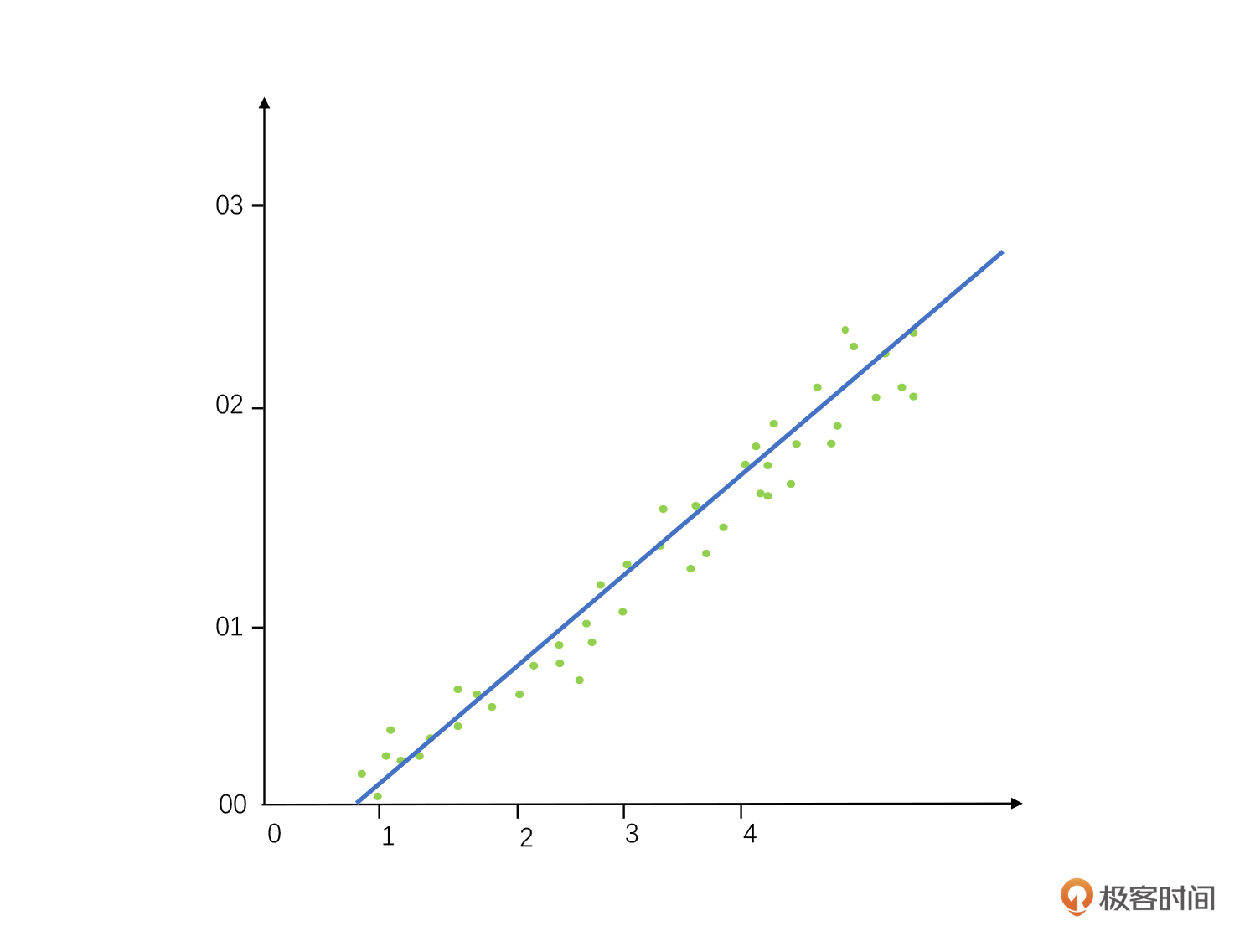
高尔顿找到了100组家庭测量了他们父母和孩子的身高,通过一元线性回归分析建立了一个公式来预测孩子和父母身高的关系,如下图。
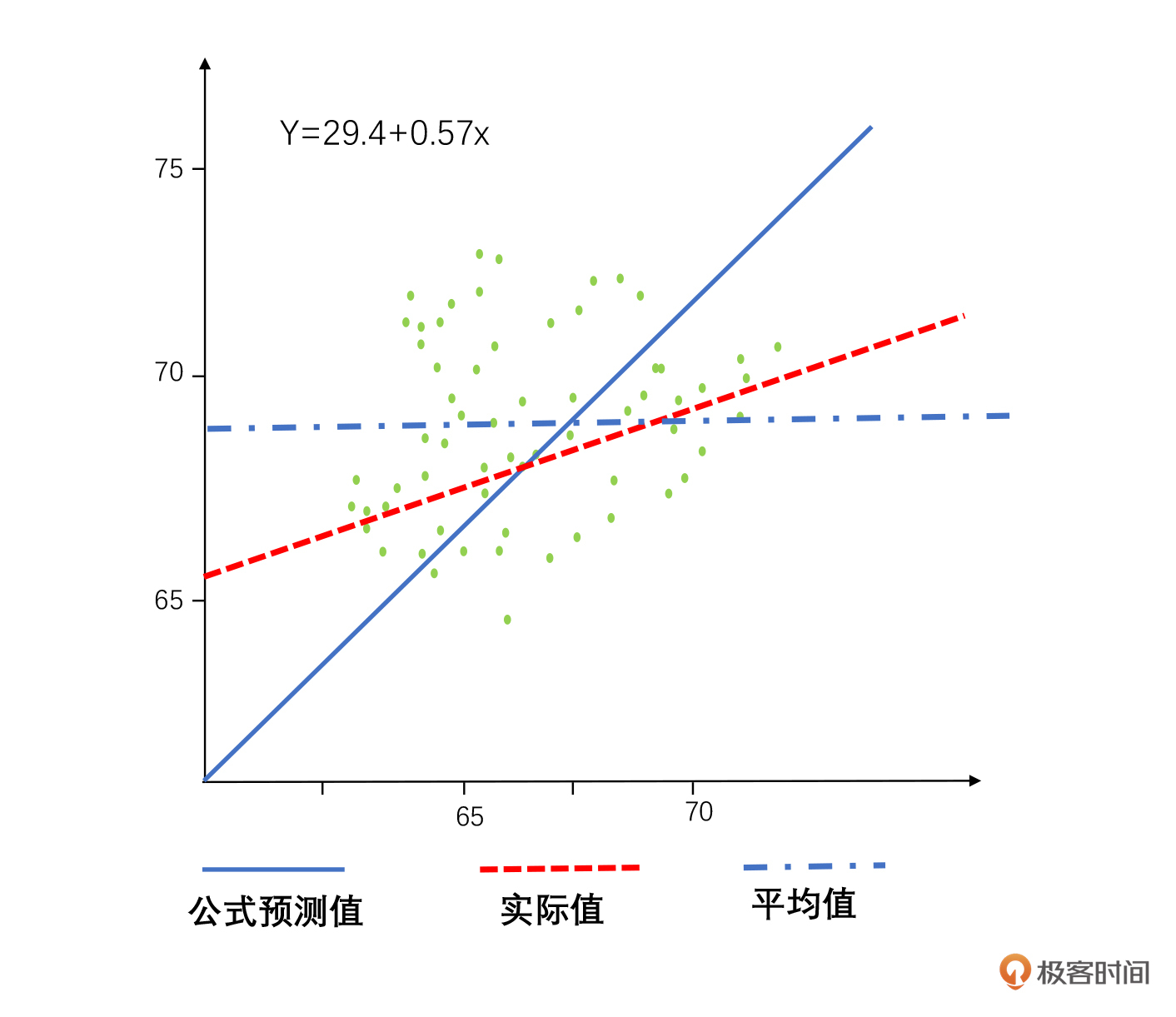
你可以通过这个图很明显地看到,通过公式计算出来的值和实际孩子最后成长的结果是不太一样的,最终孩子的身高其实趋向于平均身高。身材高大的双亲,子女不一定高;身材矮小的双亲,孩子也不一定矮。
高尔顿把这个现象叫做回归平凡,后来的统计学家把它叫做“均值回归”,意思就是实际发生的数据比我们理论上的预测更加接近平均值,整体趋势上会慢慢向一个平均值发展。比如最近比较火的一个例子,就是北大的教育学院的丁延庆教授的吐槽。
丁教授自己6岁时就能背一下整本新华字典,本科在北大,后来在哥伦比亚获得了教育学博士学位,他的妻子也是北大毕业的。丁教授与妻子都非常学霸,按理来说孩子也会走一条学霸的道路。但是丁教授的女儿却几乎完美规避了父母所有的学霸基因,在学渣的道路上越走越远。以至于丁教授在视频里面吐槽女儿“不辅导作业父慈女孝,一辅导作业鸡飞狗跳”。其实这就是均值回归的一个典型例子。
还有一个著名的例子就是美国《体育画报》的“封面诅咒”。《体育画报》是美国非常著名的一个体育杂志,但是每次杂志封面登了哪个队伍胜利之后,后面一定会有一场大败在等着这个队伍。
比如当年在俄克拉何马队连续赢得47场大学橄榄球比赛之后,《体育画报》刊登了《俄克拉何马为何战无不胜》的封面故事。紧接着在下一场比赛中,俄克拉何马队就以 21∶28输给了圣母大学队,这样的事情还发生了好几次。
其实这也是一种均值回归的情况,对于任何优秀的人和团队来说,很多时候其实是运气、能力、时机多种因素来造就成功的。好的没你想得那么好,差的也没有你想得那么差,最终还是会回到平均水平。就像我接触了很多大佬,我发现我们和最优秀的人之间,也没有那么大的智商和情商的距离,但是人家一直在坚持努力,同时再加上天时地利人和,所以他成功了。我们如果三天打鱼两天晒网,那就很难成功。
实际上,我们每天都会遇到均值回归的情况。我们不要过分夸大优秀者的能力,也不要因为某几次失败就一蹶不振,过度小看自己。只要你不懈努力,就算你现在在谷底,也最终会到达平均值水平,甚至超过平均值。
小结一下今天的内容。今天我们主要讲了回归分析,回归就是研究一个变量和另一个变量的变化关系。现在有非常多的回归算法,我着重给你讲了线性回归、逻辑回归和多项式回归这三个比较常见的算法。
紧接着,给你分享了过拟合和欠拟合这两个在数据挖掘和人工智能里常用到的概念。我们既不能过于纠结细节陷入到过拟合里,也不能神经大条错过太多的细节最后导致欠拟合。最后我还讲了均值回归的概念,万物最终都要回归自然平均。
在生活和工作里,我们可以通过回归分析找到很多简单的规律,它们能够帮助我们去预测一些常见的数据问题。但是在真正使用的时候,我们也不能盲目相信算法模型推导出来的结果,因为现实其实要比我们预测出来更加的贴近于平庸:好的没有我们预测当中的那么好,差的也没预测当中的那么差。
所以对我们自己的工作和生活来讲,用一颗平常心不断去提高自己的平均线水平才是正确选择。人和人之间的差异没有那么大,不存在着优生学,也不存在着“龙生龙凤生凤,老鼠的儿子会打洞”这样的说法。
数据给你一双看透本质的眼睛,最终所有的成果,都会回归到我们每分每秒的努力当中,我们一起努力。
你在工作和生活当中遇到过“均值回归”的情况么?你从中学到了些什么呢?分享出来,我们一起共同提高。