数据给你一双看透本质的眼睛,这里是《数据分析思维课》,我是郭炜。
前面给你讲了回归、分类、聚类、关联等一些基础算法,其实如果有足够的时间和计算资源,我们其实能通过这些基础算法做出很多特别精确的预测和分析。
但实际我们在现实工作和生活中,没那么多的资源和时间来得到最佳的结果。那么在有限时间里,怎么样才能够获得比较好的计算答案,或者有没有好的办法能够在比较短的时间求得正确的答案呢?今天我就给你分享两个比较有代表性的算法:蒙特卡洛算法和拉斯维加斯算法。
这两个算法的目标都是利用随机的方法来简化整体的算法过程,解决一些看上去我们没有办法通过正常算法解决的实际问题。
先给你讲讲蒙特卡罗算法,这个算法是在20世纪40年代,由S.M.乌拉姆和J.冯·诺伊曼首先提出来(对,就是那个世界上最早的通用电子计算机ENIAC创作者冯·诺伊曼)。
这个算法的名字由来其实很随意。那个时候,正值美国在第二次世界大战,乌拉姆和诺伊曼都是“曼哈顿计划”(美国原子弹计划)计划的成员,而第一台电子计算机ENIAC在发明后就被用于“曼哈顿计划”。在参与这个计划过程中,乌拉姆想到在计算机强大计算能力的帮助下,可以通过重复数百次模拟核实验的方式来对核裂变的各种概率变量进行演算,而不用实际进行那么多次实验。
冯·诺伊曼立即认识到这个想法的重要性并给予乌拉姆充分的支持,乌拉姆将这种统计方法用于计算核裂变的连锁反应,大大加快了这个项目的节奏。由于乌拉姆常说他叔叔在摩纳哥的赌城“Monte Carlo”输钱,他的同事Nicolas Metropolis戏称该方法为“蒙特卡罗”,这个名字也就沿用到了现在。
蒙特卡罗算法原理其实很简单,就是每次计算都尽量尝试找更好的结果路径,但不保证是最好的结果路径。用这样寻找结果的方法,无论何时都会有结果出来,而且给的时间越多、尝试越多,最终会越近似最优解。
举个例子,我们现在要用蒙特卡洛算法找到一个有500个苹果的筐里,最大的苹果。正常来讲,我们每次从筐中拿一个苹果A, 然后下一次再随机从筐中拿出另一个苹果B, 如果B比A大的话,就把A扔到另一个筐里,手里只拿着B。这样如果我们拿了500次的话,最后留在手里的一定是最大的那个苹果。
但如果我们的时间和资源不够拿500次苹果呢?
我们就可以用蒙特卡洛算法,无论我们选择多少次,每次手里依然保留比较大的苹果,直到资源不够让我们截止的时候,留在我们手上的苹果也是我们力所能及接近最大的。也就是说我们持续保留较好的答案,一直执行N次(N<500),最终拿到的一定近似正确解。N越接近500,我们的苹果越接近最大的那个。其实蒙特卡洛方法的理论基础就是我们前面讲过的大数定律。根据这个定律我们知道当随机事件发生的次数足够多时,发生的频率就会趋近于预期的概率。
和蒙特卡罗算法截然相反的另一种算法就是拉斯维加斯算法,它是在1979年László Babai在解决图同构问题的时候,针对蒙特卡罗算法弊病提出的。拉斯维加斯算法原理也很简单,就是每次计算都尝试找到最好的答案,但不保证这次计算就能找到最好的答案,尝试次数越多,越有机会找到最优解。
举个例子,假如有一把锁,给我100把钥匙,其中只有1把钥匙可以开锁。于是我每次随机抽1把钥匙去试,打不开就再换1把。我尝试的次数越多,打开锁的机会就越大。但在打开之前,那些错的钥匙都是没有用的。这个挨个尝试换钥匙开锁的算法,就是拉斯维加斯算法。
准确来讲,蒙特卡罗算法和拉斯维加斯算法其实并不是两种算法,而是两类算法的统称。
蒙特卡罗算法的基本思想是精益迭代,进行多次求解,最终让最后结果成为正确结果的可能性变高。而拉斯维加斯的算法是不断进行尝试,直到某次尝试结果让你自己满意,当然这个过程中也会一直产生你无法满意的随机值。
所以拉斯维加斯的算法效率通常比蒙特卡罗的算法低,但是最终得出的解一定是这个问题的正确解,当然也有可能无法得到问题的解。这两个算法之间的差别你可以通过下面的这个图表来进行区分。

刚刚从概念上带你了解了蒙特卡罗算法和拉斯维加斯算法,下面我实际给你举两个具体的例子来看看这两个算法的进一步运用。
首先我们来看看利用蒙特卡罗算法计算圆周率。
圆周率是通过n个多边形周长来推导计算出来的(可以参考附录),不过我们通过蒙特卡罗算法,也可以把圆周率计算出来。
首先,我们构造一个正方形,里面套一个内切圆。
然后,我们在这个正方形的内部随机打上1万个点。
最后,根据它到中心点的距离来判断这个点是否落在圆的内部。这个落在圆内部的概率其实和这个圆与正方形之间的面积有一个比例关系。也就是假设落在圆内的概率为P,则P=圆面积/正方形面积。P=(π*R*R)/(2R*2R)= π/4也就是 π=4P。
如果我们的这些点是足够均匀分布的,那么圆内的点应该占到整个正方形里面点的π/4,所以只要把这个概率P乘以4就是π的值。

具体步骤如下。
1.将圆心设在原点,以R为半径作圆,则第一象限的1/4圆面积为π*R*R/4;
2.做该1/4圆的外接正方形,坐标为(0,0)(0,R)(R,0)(R,R),则该正方形面积为R*R;
3.随机取点(X,Y),使得0<=X<=R并且0<=Y<=R,即点在正方形内;
4.通过公式 X*X+Y*Y<RR判断点是否在圆内;
5.最后一共模拟了N次试验,一共有M个点在圆内,则P=M/N,而π=4*M/N。
这个N就是蒙特卡洛算法的特点,N越大,越接近π的真实值,但是你可以设置任何一个时刻停下来都会有一个接近正确答案的值。我在一个平台上用这个算法进行计算,发现如果N是1万个点的话,它的结果是3.1424。是不是很神奇?我们并没有通过数学推导的方式,而是通过一个随机变量的方式来计算出我们的结果。如果你要提高精确度,我们可以打上更多个点,那么它最终会越来越接近π真实值。
而拉斯维加斯算法就不一样了,它是针对一个确定性的答案去不断进行随机尝试,我再给你举一个国际象棋里“摆皇后”的例子。
我们的目标是在一个N*N国际象棋棋盘里摆下N个皇后,让她们相互不会被吃掉。例如,下面这个图我们就摆了8个皇后在标准的8×8的国际象棋棋盘中,在这棋盘里,她们可以不相互伤害,和平共处。

这个摆法我们是怎么摆出来的呢?
一般解法是先在最左边(1,1)摆上第1个皇后,然后再把第2个摆放到第一个不被吃的位置(2,3),再把第3个摆进去不被吃的位置……这样一直延续下去,直到无论下一个皇后摆在哪都会被吃掉的时候,证明上面几个皇后摆放的位置不对。那么你就要去挪上一个皇后的位置,如果还不行还得再挪上上个皇后,然后再摆下一个皇后。
这样不停尝试下去,才能把N个皇后都摆进这个N*N的格子里。可以想象,这个算法毛病就在于你得不停地去做尝试。这个算法的代价就很大,经过数学的推理,找到最终解决方案的尝试次数,数量级在N的N次方。这样如果当皇后数超过15个的时候,这个数字就会达到437893830380853000次——基本上现在普通电脑的计算能力短时间内就计算不出来了。
怎么解决这个问题呢?我们首先看前面小规模的8*8、10*10棋盘里,皇后在棋盘上摆的正确位置,其实并没有什么规律可言,就像随机放在上面的。于是我们就可以想象一下,如果用拉斯维加斯算法把皇后类似于随机地摆放在棋盘上,然后在用前面的算法进行调整,是不是就会比我们一个一个放速度要快呢?也就是说我们先利用拉斯维加斯算法在前面若干行随机摆放皇后,后面的行再利用前面传统的算法去完成。实际结果证明可以节约很多计算的时间和资源。
一旦用拉斯维加斯算法找到一个解,这个解就一定是正确解,但有时用拉斯维加斯算法找不到解。拉斯维加斯算法找到正确解的概率随着它所用的计算时间的增加而提高,那么,对于某一个难题来说,如果你用同一拉斯维加斯算法反复尝试足够多次,可使求解失败的概率任意小,最终还可以获得正确解答。
通过这个算圆周率和“摆皇后”的例子,不知道你对这两个算法各自的优点有没有进一步的认识呢?
现在,蒙特拉罗和拉斯维加斯算法在金融工业和人工智能领域都有很广泛的应用。特别是蒙特卡罗算法,在当今社会有各种各样不确定性的情况下,它给我们提供了很多解决方案。
比如金融市场本身充满了确定性和不确定性,就非常符合蒙特卡洛面对数字化变量的确定性和随机性这两种特征。使用蒙特卡洛算法利用尽可能多的模型采样,就可以寻求近似最优解。所以在金融领域里,蒙特卡洛算法得到非常广泛的应用。
在人工智能领域,蒙特卡洛也必不可少。现在人工智能领域里为了简化复杂的计算而产生了一个很重要的算法叫做蒙特卡洛树。以现在特别火的人工智能下棋的算法来讲,基本思路是每一步AI去判断的下一步的运算时间、内存空间都是有限的,而且不能要求最优解,所以阿尔法狗和类似的AI下棋算法,一定会利用蒙特卡洛方法来简化其中的步骤,获得相对最优下棋的方法。毫无疑问,蒙特卡洛算法会是这个场景下的核心算法之一。
如何在这两类随机算法之间选择,那就要具体问题具体分析了。如果问题要求在有限时间和尝试次数内必须给出一个解,但不要求是最优解,那就用蒙特卡罗算法。反之,如果问题要求必须给出最优解,但对时间和尝试次数没有限制,那就用拉斯维加斯算法。
把这两种算法对应到工作和生活中,对拉斯维加斯算法来说,有些事情我们是需要精益求精,无论花多少时间都得把这件事情做细致做准确,否则后果可能会非常严重;有些地方反而是需要蒙特卡洛算法,在事情有大概比较清晰的方案的时候,要快速决策,否则如果把时间耽误了,反而最后获得的结果会更糟。
给你举个具体的例子,现在在工作上有一种创业方法叫做“精益”创业,其实核心思想就是和蒙特卡洛算法类似:在有限的时间和有限的资源情况下,不要一直思考或者规划找到“最优解”,而是通过快速迭代原型产品,通过用户的反馈不断地修正自己产品的方案,以达到在有限的时间和有限的资源情况下得到较为不错的结果。
虽然这个结果不一定是最优的,但是总比使用拉斯维加斯算法创业,闷在家里闭门造车寻找最优解,直到耗尽了资源和时间要好。
总结一下,今天主要给你讲了两个算法:蒙特卡洛算法和拉斯维加斯算法。
蒙特卡洛算法是我们一直去努力,努力到自己满意了就可以停下来;而拉斯维加斯算法就要一直去努力,如果找不到最佳答案就誓不罢休。这两个算法其实是两类算法集合,代表着两种不同处理事情的思路。
我们要根据自己手里的资源、时间,灵活选择是使用蒙特卡罗式的方法还是拉斯维加斯式的方法来处理事情,毕竟人的一生时间和精力都是有限的。
我们每天都会面临到各种各样的问题,学完这节课后,你可以仔细思考一下你现在手里哪些事情不达目的誓不罢休(拉斯维加斯式算法);哪些事情需要精益的方法和思路,多次尝试不断修正,事情发展到一定程度见好就收(蒙特卡洛式算法)。
对于管理企业来说,我们要高维度思考,不要把我们的有限的时间和精力浪费在不必要的事情上,整体的做事思路是抓大放小。而重要的事情要用拉斯维加斯算法一通到底,任何细节都不要放过,确保随机事件的正确性。
一次次不同的决策,决定了每一个企业成功和失败。同样,一次次我们自己不同的决策,也决定了我们别具特色的人生。
数据给你一双看透本质的眼睛,针对具体的场景问题选择好具体的算法解决方式,把我们有限的时间和精力投入到真正要做的事情当中。
你在工作和生活当中用过蒙特卡洛和拉斯维加斯算法的思路来解决问题么?分享出来,我们大家相互启发。
π数值的算法最早是公元前250年由希腊数学家阿基米德所发明,算法逻辑很简单,也就是在圆内接和外切套入两个多边形。理论上,圆的周长在这两个多边形之间,多边形的周长我们有公式计算,圆的半径已知,多边形的边长就已知。那么只要把这个多边形的边数增加越多,那么多边形的周长也就越来越接近圆的周长,反推出来的π也就越精确。
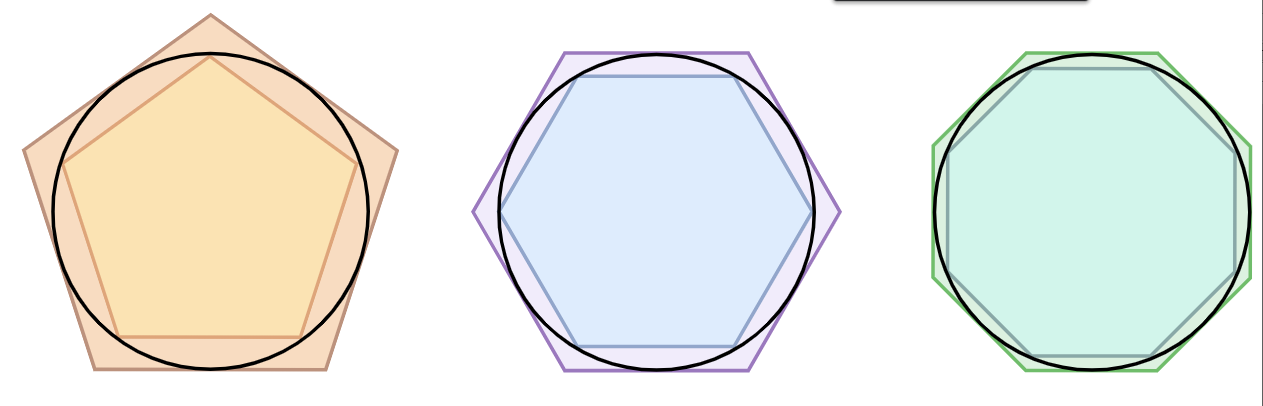
阿基米德利用96边形推算出来的π值在3.1408和3.1429之间,在公元前150年,希腊罗马的科学家克劳狄乌斯·托勒密在《天文学大成》一书中提到π的数值是3.1416。在1630年多名数学家利用多边形的方式计算π到第39位小数,一直到1699年,其他数学家才利用无穷级数的方式打破其纪录,计算到第71位小数。多边形计算法是第一个有纪录、严谨计算π数值的算法。