在上一讲中我提到，深度学习既可以用于解释也可以用于预测。在实际中，这两个功能通常被组合使用，解释功能可以看作编码器，对高维信息进行低维重构；预测功能则可以看作解码器，将低维重构恢复成高维信息。

这样的两个深度网络级连起来，就形成了编码-解码结构（encoder-decoder model）。这种结构在诸如语音、文本、图像等高维数据的处理中应用广泛，取得了良好的效果。

编解码的思想来源于信息论，是信息传输与处理的基础理论之一。但在通信中，编解码的对象是底层的语法结构，也就是对携带信息的符号进行编码，通过数据压缩实现信息的高效传输，但输出的符号本身与其所表达的含义并无关联。

在深度学习中，编解码的操作更多在语义层面完成，无论是文本还是图像，编解码的目的都是重新构造数据的表示方式，简化学习任务的难度。

在最初的尝试中，编码器和解码器并不是分开的，而是存在于单个的深度网络中，这种深度结构就是自编码器。

自编码器（autoencoder）属于生成模型，它的作用是以无监督的学习方式学到数据集的稀疏表示，从而给数据降维。显然，它和前面介绍过的主成分分析殊途同归。可以证明，如果自编码器只有一个线性隐藏层，同时使用均方误差作为损失函数，那么$k$个隐藏神经元的权重系数就代表了输入数据的$k$个主成分。

从编解码的全过程来看，如果要构造出有效的表示，自编码器的输入和输出就应该是近似相等的，那它学习的对象是个恒等函数。看到这儿你可能就不理解了：恒等函数有什么好学的呢，原样输入原样输出不就完了吗？这话一点儿毛病没有，但成立的前提是原样输入原样输出的功能可以实现。

这就像学美术的学生需要临摹画作，再高的临摹技术也比不过手机拍照来得像，但你拿一张照片去跟老师交差肯定是要挨骂的。自编码器要研究的不光是如何近似恒等函数，而是如何用50个中间变量构造出包含100个自变量的恒等函数，这样的问题就没那么简单了。

需要说明的是，在结构上，自编码器隐藏神经元的数目未必会少于输入/输出神经元。但即使有200个隐藏的神经元，自编码器通常也只会激活这些潜在中间变量里的一小部分，达到的效果仍然是用50个中间变量拟合100维的恒等函数，这种即使在过完备时依然得以保持的稀疏特性（sparsity）是自编码器实现降维的核心特性。

自编码器的稀疏特性可以从能量的角度来解释。在自编码器最初的设计中，编码器的任务是生成参数矩阵${\bf W}_C$，用来计算输入数据$\bf X$的码字向量，解码器的任务是生成参数矩阵${\bf W}_D$，用来重构的码字向量所对应的初始数据$\tilde{\bf X}$。

如果编码器和解码器直接级连的话，这就是个主成分分析的系统。但自编码器和主成分分析的区别在于引入了稀疏逻辑模块（sparsifying logistic），将编码器输出的码字$\bf Z$非线性地映射成特征码字$\bar{\bf Z}$。特征码字大部分元素的取值为0，非零元素值则落在[0, 1]这个区间内。

定义损失函数时，自编码器将非线性的编解码过程综合考虑，提出了能量（energy）的概念，其数学表达式为

$$ E({\bf X}, {\bf Z}, {\bf W}_C, {\bf W}_D) = E_C({\bf X}, {\bf Z}, {\bf W}_C) + E_D({\bf X}, {\bf Z}, {\bf W}_D) = \dfrac{1}{2} || {\bf Z} - {\bf W}_C{\bf X} || ^ 2 + \dfrac{1}{2} || {\bf X} - {\bf W}_D\bar{\bf Z} || ^ 2 $$

其中的第一项表示编码器的预测能量（prediction energy），第二项表示译码器的重构能量（reconstruction energy），作为两者之间接口的稀疏逻辑则具有以下的非线性映射关系

$$ {\bar z}_i(k) = \dfrac{\eta e ^ {\beta z_i(k)}}{\xi_i(k)}, \xi_i(k) = \eta e ^ {\beta z_i(k)} + (1 - \eta)\xi_i (k - 1) $$

其中$k$表示第$k$个训练样本，$i$表示特征码字中的第$i$个元素。通过$\xi_i(k)$的递归表达式可以看出，稀疏逻辑的本质就是计算所有训练样本中相同码字单元的加权softmax分类结果，其中的参数$\eta$控制特征码字的稀疏程度，$\eta$越小非零元素越少；参数$\beta$则控制特征码字的平滑程度，$\beta$越大码字的输出就越接近两点分布。通过合理地增大$\beta$并减小$\eta$，自编码器就可以实现稀疏的表示。

将编码器和解码器整合到同一个结构之中的自编码器可以说是个特例，它的编码器和解码器都可以堆叠成层次化的结构，来实现更加复杂的非线性映射。在自编码器的基础上推广一步，将编码器和解码器各自作为一个独立的深度网络区分开来，可以实现更加强大的功能。

《红黄蓝之构成》（Composition II in Red, Blue and Yellow）（1930）（图片来自维基百科）

上面这张图片是荷兰大师皮埃·蒙德里安（Piet Mondrian）的名作《红蓝黄之构成》（Composition II in Red, Blue and Yellow），可不要小看这幅画，这个看似简单的色块组合摆到拍卖行就是千万美元起步的价格。当然，我的目的不是讨论几何抽象画派的艺术造诣，而是要从稀疏表示的角度来看待这幅画。

显然，这张图像中的像素只有少数几种取值，而相同取值的像素又基本上集中在一起。如果将每一组聚合在一起的颜色相同的像素用一串编码来表示，就可以大大地压缩这幅《构成》的体积，这就是所谓的游程编码（run length coding）。

同样的思路也可以应用到图像的语义处理之中。从语义上看，《构成》其实就是不同颜色的几何形状的组合，而每个形状的特征无外乎长度、宽度和颜色这样三个维度，对图像的学习实际上就是对这三个维度的学习。

在“人工智能基础课”中我介绍过卷积神经网络，这是基于神经网络的图像处理使用的最主要的工具。卷积神经网络本身就可以看成是个庞大的编码器，其中的卷积层用于提取特征，不同的卷积核（convolutional kernel）代表不同的特征类型。

在图像的每个局部上，和卷积核相似度最高的区域都被下采样操作（subsampling）筛选出来，用于下一阶段的特征提取。在卷积层和下采样层的迭代过程中，低层次的特征不断组合成高层次的特征，数字图像的表示方式也从原始的像素集合变成卷积得到的特征组合，这两个层也就构成了卷积神经网络的编码器。

对卷积出来的表示进行解码相当于反转编码的过程，编码的输出经过上采样的处理之后再和卷积核进行卷积。上采样（upsampling）不仅可以补充缺失分辨率，还能确定编码器学到的码字中每个元素的覆盖范围，卷积操作则在覆盖范围上计算上采样结果和特征本身的匹配程度。

随着上采样和卷积的不断进行，高层次的特征如庖丁解牛般一点点被拆解成低层次的特征，这些特征在重构出的图像中又体现为像素的分类结果。如此这般，一个完整的卷积网络编解码可以将原始图像重构成不同语义的组合，来自斯坦福大学CS231n课程的下图就是个典型的例子。

卷积网络编解码

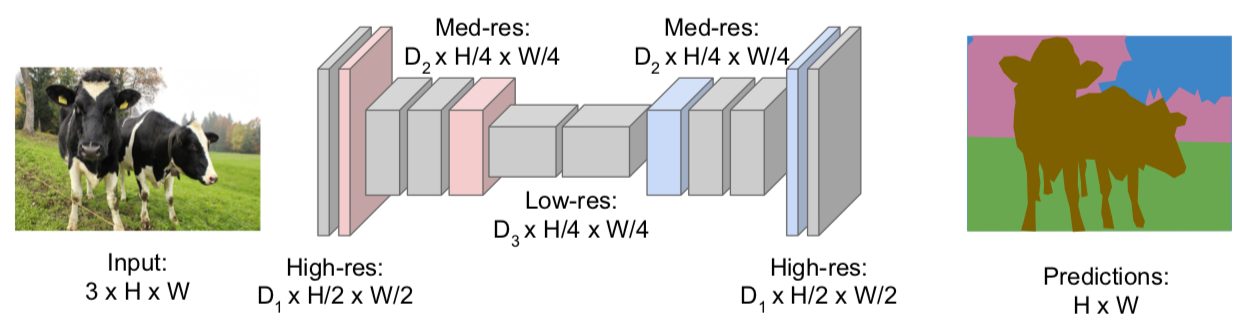
（图片来自http://cs231n.stanford.edu/slides/2017/
cs231n_2017_lecture11.pdf）

和卷积网络相比，编解码结构更直观的应用是在循环神经网络中。循环神经网络是增加了时间维度的神经网络，是自然语言处理、尤其是机器翻译的利器。机器翻译需要将一种语言的句子映射成另一种语言的句子，这类序列到序列的模型（sequence-to-sequence model）正是编解码结构的用武之地。

不管使用循环神经网络还是长短期记忆网络，编解码结构在处理翻译问题时都是整体读取输入的语句，将输入语句编码成定长的向量码字表示。在带有时序的神经网络中，编码的码字会以隐藏状态的形式出现，并被编码器分字翻译成输出。在译码时，译码器会根据隐藏状态和之前时刻的输出来确定当前时刻输出的似然概率，并选择最优的结果。

在谷歌的招牌神经机器翻译系统（Google neural machine translation）中，编码器和译码器中不同的长短期记忆层以残差连接，以提升反向传播中的梯度流，加快深层网络训练的速度。编码器网络的最底层和解码器网络的最顶层通过注意力模块进行连接，其作用在于使译码器网络在译码过程中分别关注输入语句的不同部分。其中具体的细节在这里就不做介绍了。

编码器和译码器并不一定非要具有相同的类型，异构的神经网络一样可以用来构成编解码结构。在微软公司于2017年自然语言处理实证方法会议（Conference on Empirical Methods in Natural Language Processing）发表的论文《利用卷积神经网络学习语句的通用表示》（Learning generic sentence representations using convolutional neural networks）中，研究者就提出了一种学习文本分布式表示的架构。

这种架构以卷积神经网络作为编码器，将输入语句转化为连续取值的码字，译码器则采用长短期记忆网络。之所以选择卷积网络作为编码器，作者的解释是一是卷积网络可以达到稀疏的效果，降低参数的数目；二是卷积网络的层次化结构有助于识别语句中的语言模式，这是循环网络无法做到的。

除了文本处理外，图像处理也可以应用到异构的编解码结构。在韩国研究者的论文《用于图像捕捉的文本导向注意力模型》（Text-guided attention model for image caption）中，作者使用一个卷积网络对待捕捉的图像编码，用一个循环网络对包含捕捉对象的文本编码，两者的输出用注意力机制处理后再对卷积网络的输出进行加权。译码器则利用长短期记忆网络将码字转换成语句。感兴趣的话，你可以自己阅读文章，了解细节。

编解码结构的核心是生成数据的表示，因而属于表示学习的范畴。表示学习（representation learning）也叫特征学习（feature learning），其目标是让机器自动发现原始数据中与输出相关度较高的隐含特征，因而能够自动生成新特征的技术都可以归纳到表示学习中。

今天介绍的编解码结构则可以看成是表示学习的一类应用。《表示学习：综论与新视角》（Representation Learning-A Review and New Perspectives）是关于表示学习的一篇综述，如果想深入了解表示学习，可以阅读这篇文献。

今天我和你分享了由深度网络衍生出来的编解码结构，以及相关的表示学习概念，包含以下四个要点：

和特征学习相对应的概念是特征工程（feature engineering），也就是人工提取数据特征。这样做虽然能够充分利用垂直领域的先验知识，却在效率上远远逊色。那么你是如何看待特征学习与特征工程的利弊与结合的呢？

欢迎发表你的观点。

评论