你好,我是李智慧。
在04讲中,我们讨论了大型分布式网络爬虫的架构设计,但是网络爬虫只是从互联网获取信息,海量的互联网信息如何呈现给用户,还需要使用搜索引擎完成。因此,我们准备开发一个针对全网内容的搜索引擎,产品名称为“Bingoo”。
Bingoo的主要技术挑战包括:
一个完整的搜索引擎包括分布式爬虫、索引构造器、网页排名算法、搜索器等组成部分,Bingoo的系统架构如下。

分布式爬虫通过存储服务器将爬取的网页存储到分布式文件集群HDFS,为了提高存储效率,网页将被压缩后存储。存储的时候,网页一个文件挨着一个文件地连续存储,存储格式如下。

每个网页被分配得到一个8字节长整型docID,docID之后用2个字节记录网页的URL的长度,之后4个字节记录压缩后网页内容数据的长度,所有存储的网页的头14个字节都是同样的格式。之后存储URL字符串和压缩后的网页内容数据。读取文件的时候,先读14个字节的头信息,根据头信息中记录的URL长度和数据长度,再读取对应长度的URL和网页内容数据。
搜索引擎能够快速查找的核心就是利用索引,根据用户的查询内容查找匹配的索引,根据索引列表构建结果页面。索引的构造主要通过索引构造器完成,索引构造器读取HDFS中的网页内容,解压缩后提取网页中的单词,构建一个“docID->单词列表”的正排索引。然后,索引构造器再根据这个正排索引构建一个“单词->docID列表”的倒排索引,“docID列表”就是包含了这个单词的所有网页列表。利用这个倒排索引,搜索器可以快速获得用户搜索词对应的所有网页。
网页中所有的单词构成了一个词典,实际上,词典就是一个Hash表,key就是单词,value就是倒排索引的网页列表。虽然互联网页的内容非常庞大,但是使用到的单词其实是非常有限的。根据Google的报告,256M内存可以存放1400万个单词,这差不多就是英文单词的全部了。
在构建索引的过程中,因为要不断修改索引列表,还要进行排序,所以,有很多操作是需要进行加锁同步完成的。对于海量的互联网页的计算,这样的索引构建速度太慢了。因此我们设计了64个索引桶,根据docID取模,将不同网页分配到不同的桶中,在每个桶中分别进行索引构建,通过并行计算来加快索引处理速度。
索引构造器在读取网页内容、构造索引的时候,还会调用URL提取器,将网页中包含的URL提取出来,构建一个链接关系表。链接关系表的格式是“docID->docID”,前一个docID是当前网页的docID,后一个docID是当前网页中包含的URL对应的docID。一个网页中会包含很多个URL,也就是会构建出很多个这样的链接关系。后面会利用这个链接关系表,使用PageRank排名算法对所有网页进行打分排名,当索引器得到查找的网页列表时,利用PageRank值进行排名,最终呈现给用户,保证用户最先看到的网页是最接近用户期望的结果页面。
一个运行良好的搜索引擎的核心技术就是索引和排名,所以我们将分别说明这两种技术要点。
索引构造器从HDFS读取网页内容后,解析每个页面,提取网页里的每个单词。如果是英文,那么每个单词都用空格分隔,比较容易;如果是中文,需要使用中文分词器才能提取到每个单词,比如“高并发架构”,使用中文分词器得到的就是“高并发”、“架构”两个词。
首先,索引构造器将所有的网页都读取完,构建出所有的“docID->单词列表”正排索引。

然后遍历所有的正排索引,再按照“单词→docID列表”的方式组织起来,就是倒排索引了。
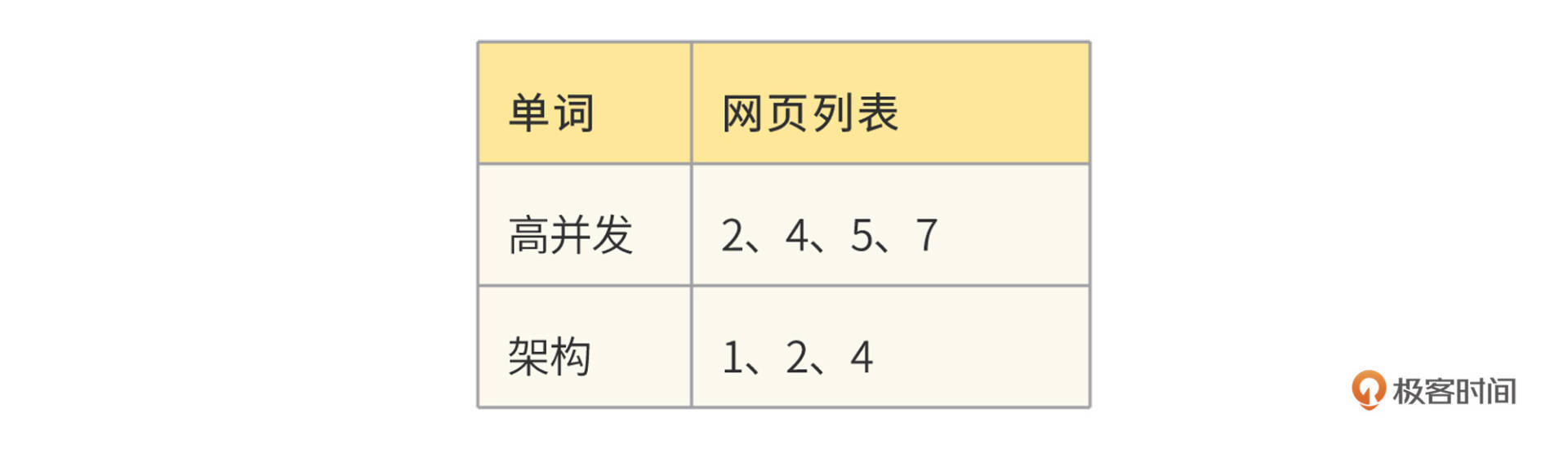
我们这个例子中只有两个单词、7个网页。事实上,Bingoo数以千亿的网页就是这样通过倒排索引组织起来的,网页数量虽然庞大,但是单词数却是比较有限的。所以,整个倒排索引的大小相比于网页数量要小得多。Bingoo将每个单词对应的网页列表存储在硬盘中,而单词则存储在内存的Hash表,也就是词典中,词典示例:
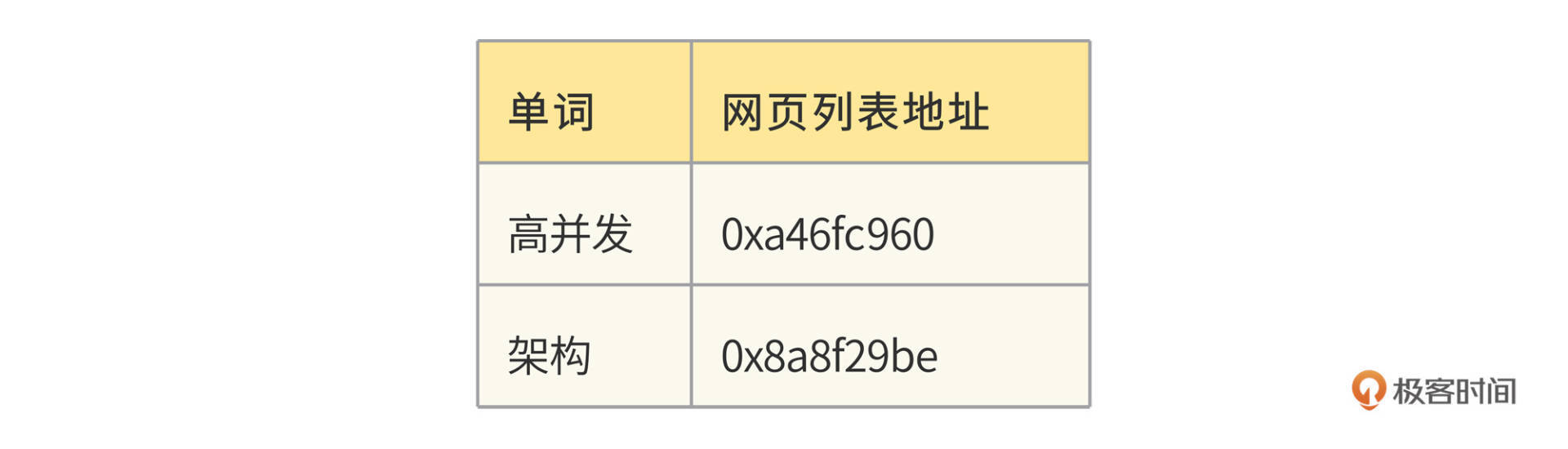
对于部分热门的单词,整个网页列表也可以存储在内存中,相当于缓存。在词典中,每个单词记录下硬盘或者内存中的网页列表地址,这样只要搜索单词,就可以快速得到对应的网页地址列表。Bingoo根据列表中的网页编号docID,展示对应的网页信息摘要,就完成了海量数据的快速检索。
如果用户的搜索词正好是一个单词,比如“高并发”,那么直接查找词典,得到网页列表就完成查找了。但是如果用户输入的是一个句话,那么搜索器就需要将这句话拆分成几个单词,然后分别查找倒排索引。这样的话,得到的就是几个网页列表,还需要对这几个网页列表求交集,才能得到最终的结果列表。
比如,用户输入“高并发架构”进行搜索,那么搜索器就会拆分成两个词:“高并发”、“架构”,得到两个倒排索引:
高并发->2,3,5,7
架构->1,2,4
需要对这两个倒排索引求交集,也就是同时包含“高并发”和“架构”的网页才是符合搜索要求的结果,最终的交集结果应该是只有一篇网页,即docID为2的满足要求。
列表求交集最简单的实现就是双层for循环,但是这种算法的时间复杂度是O(n^2),我们的网页列表长度(n)可能有千万级甚至更高,这样的计算效率太低。
一个改进的算法是拉链法,我们将网页列表先按照docID的编号进行排序,得到的就是这样两个有序链表:
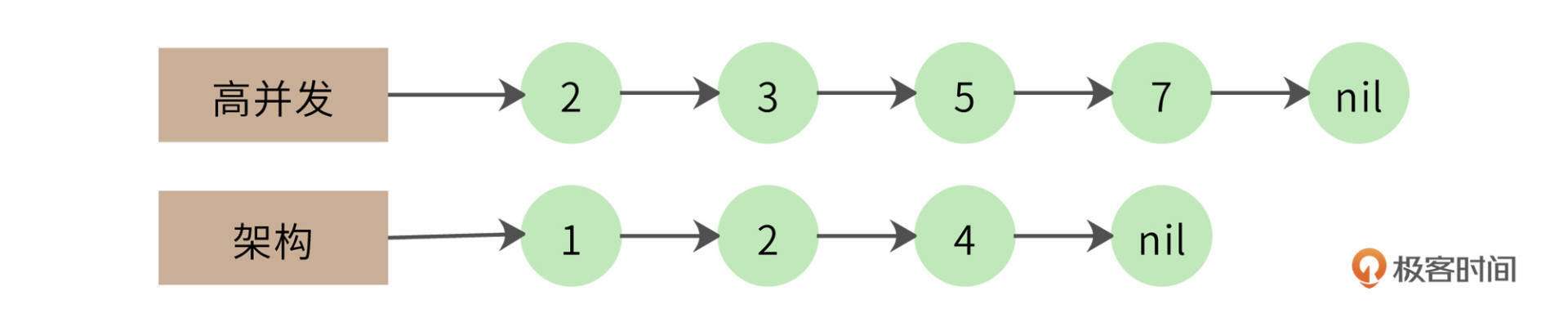
同时遍历两个链表,如果其中一个链表当前指向的元素小于另一个链表当前指向的元素,那么这个链表就继续向前遍历;如果两个链表当前指向的元素相同,该元素就是交集元素,记录在结果列表中;依此继续向前遍历,直到其中一个链表指向自己的尾部nil。
拉链法的时间复杂度是O(2n),远优于双层循环。但是对于千万级的数据而言,还是太慢。我们还可以采用数据分片的方式进行并行计算,以实现性能优化。
比如,我们的docID分布在[0, 1万亿)区间,而每个倒排索引链表平均包含1千万个docID。我们把所有的docID按照1千亿进行数据分片,就会得到10个区间[0, 1千亿)[1千亿,2千亿)……[9千亿,1万亿)。每个倒排索引链表大致均匀分布在这10个区间,我们就可以依照这10个区间范围,将每个要遍历的链表切分为10片,每片大约包含1百万个docID。两个链表只在自己对应的分片内求交集即可,因此我们可以启动10个线程对10个分片进行并行计算,速度可提高10倍。
事实上,两个1千万长度的链表求交集,最终的结果可能不过几万,也就是说,大部分的比较都是不相等的。比如下面的例子。
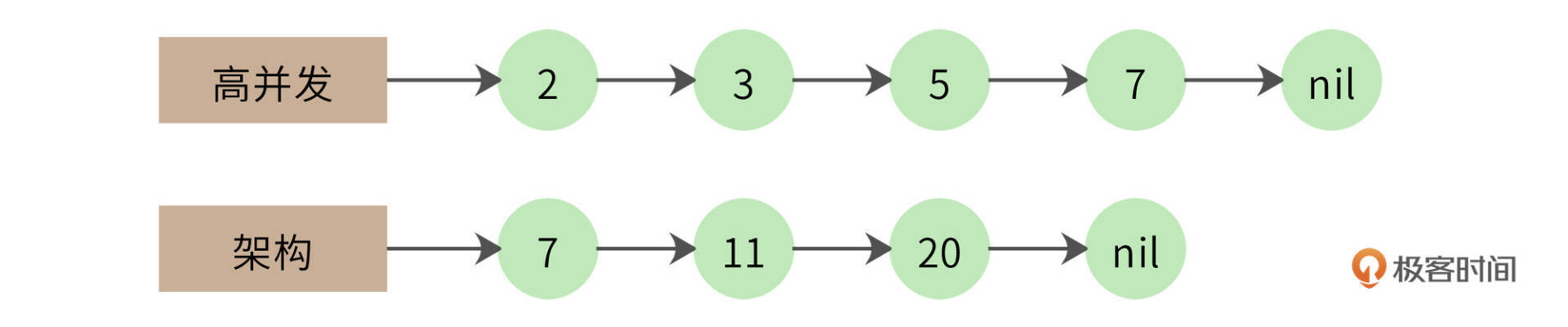
第一个链表遍历到自己的最后一个元素,才和第二个链表的第一个元素相同。那么第一个链表能不能跳过前面那些元素呢?很自然,我们想到可以用跳表来实现,如下图。
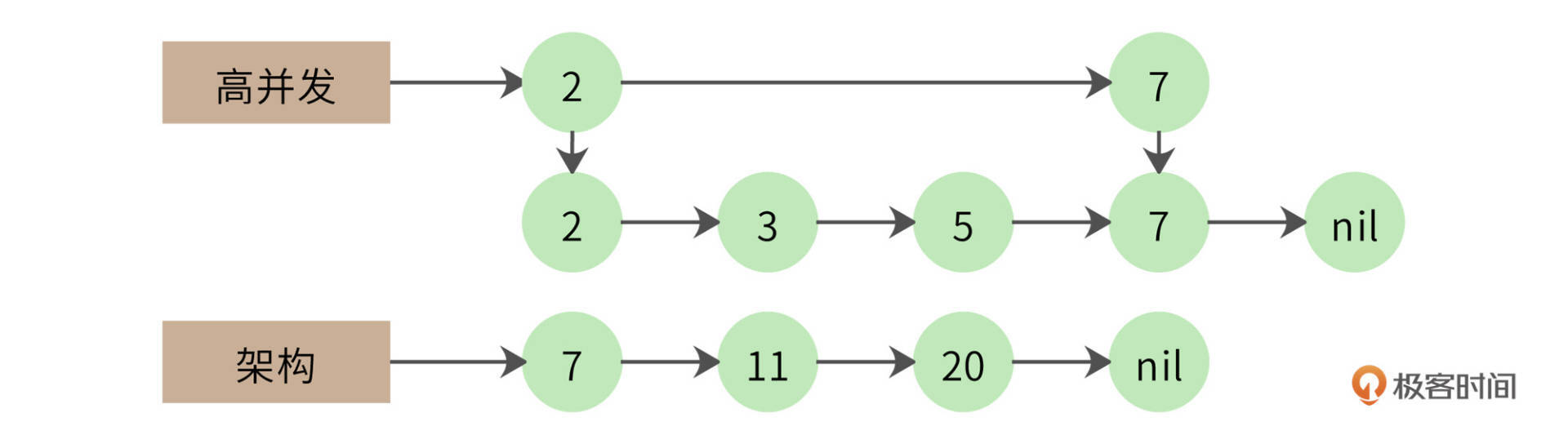
跳表实际上是在链表上构建多级索引,在索引上遍历可以跳过底层的部分数据,我们可以利用这个特性实现链表的跳跃式比较,加快计算速度。使用跳表的交集计算时间复杂度大约是O(log(n))。
此外,虽然搜索引擎利用倒排索引已经能很快得到搜索结果了,但搜索引擎应用还会使用缓存对搜索进行加速,将整个搜索词对应的搜索结果直接放入缓存,以减少倒排索引的访问压力,以及不必要的集合计算。
Bingoo使用PageRank算法进行网页结果排名,以保证搜索结果更符合用户期待。
PageRank算法会根据网页的链接关系给网页打分。如果一个网页A包含另一个网页B的超链接,那么就认为A网页给B网页投了一票。一个网页得到的投票越多,说明自己越重要;越重要的网页给自己投票,自己也越重要。
PageRank算法就是计算每个网页的PageRank值,最终的搜索结果也是以网页的PageRank值排序,展示给用户。事实证明,这种排名方法非常有效,PageRank值更高的网页,确实更满足用户的搜索期望。
以下面四个网页A、B、C、D举例,带箭头的线条表示链接。
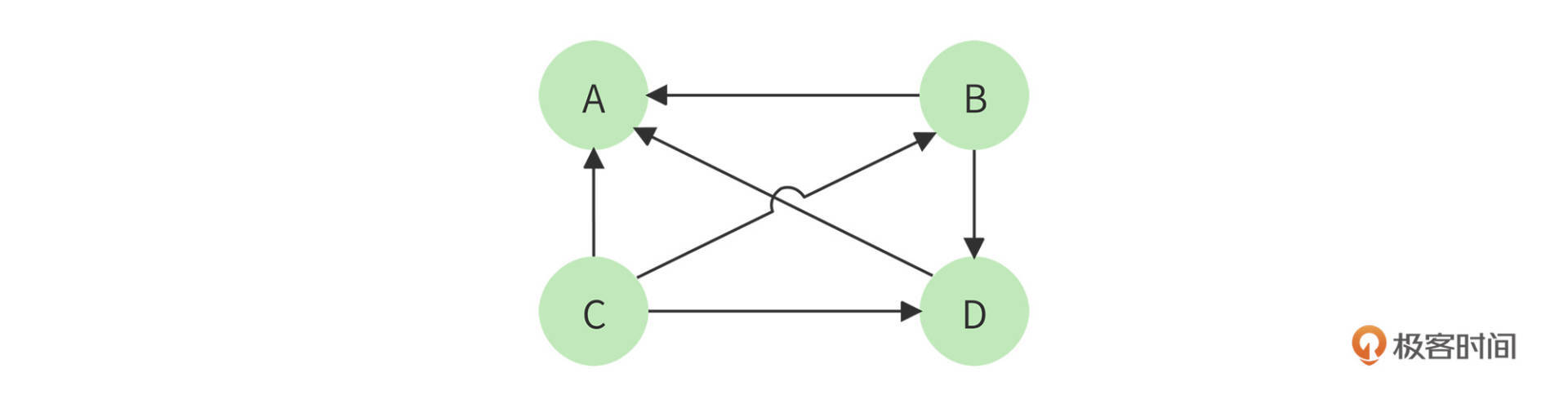
B网页包含了A、D两个页面的超链接,相当于B网页给A、D每个页面投了一票,如果初始的时候,所有页面都是1分,那么经过这次投票后,B给了A和D每个页面1/2分(B包含了A、D两个超链接,所以每个投票值1/2分),自己从C页面得到1/3分(C包含了A、B、D三个页面的超链接,每个投票值1/3分)。
而A页面则从B、C、D分别得到1/2,1/3,1分。用公式表示就是
$\small PR(A) = \frac{PR(B)}{2}+\frac{PR(C)}{3}+\frac{PR(D)}{1}$
等号左边是经过一次投票后,A页面的PageRank分值;等号右边每一项的分子是包含A页面超链接的页面的PageRank分值,分母是该页面包含的超链接数目。
这样经过一次计算后,每个页面的PageRank分值就会重新分配,重复同样的算法过程,经过几次计算后,根据每个页面PageRank分值进行排序,就得到一个页面重要程度的排名表。根据这个排名表,将用户搜索出来的网页结果排序,排在前面的通常也正是用户期待的结果。
但是这个算法还有个问题,如果某个页面只包含指向自己的超链接,其他页面不断给它送分,而自己一分不出,随着计算执行次数越多,它的分值也就越高,这显然是不合理的。这种情况就像下图所示的,A页面只包含指向自己的超链接。
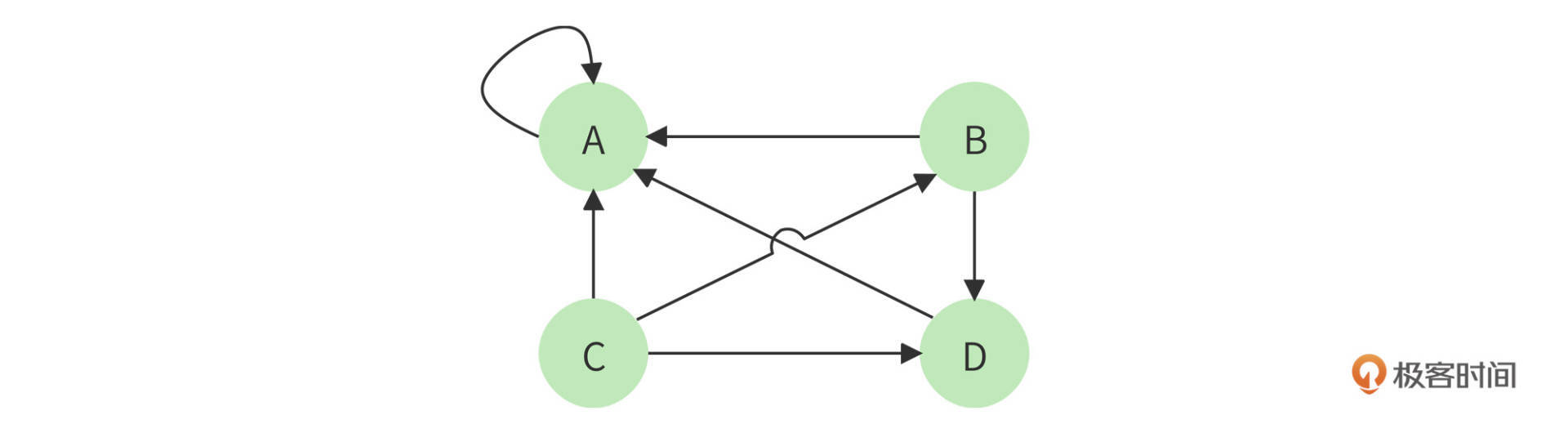
解决方案是,设想浏览一个页面的时候,有一定概率不是点击超链接,而是在地址栏输入一个URL访问其他页面,表示在公式上,就是
$\small PR(A) = \alpha(\frac{PR(B)}{2}+\frac{PR(C)}{3}+\frac{PR(D)}{1})+\frac{(1-\alpha)}{4}$
上面$\small (1-\alpha)$就是跳转到其他任何页面的概率,通常取经验值0.15(即$\small \alpha$ 为0.85),因为有一定概率输入的URL是自己的,所以加上上面公式最后一项,其中分母4表示所有网页的总数。
那么对于N个网页,任何一个页面$\small P_{i}$的PageRank计算公式如下:
$\small PageRank(P_{i})=\alpha \sum_{P_{j}\in M(P_{i})}^{}{\frac{PageRank(P_{j})}{L(P_{j})}} + \frac{1-\alpha}{N}$
公式中,$\small P_{j}\in M(P_{i})$ 表示所有包含有$\small P_{i}$超链接的$\small P_{j}$,$\small L(P_{j})$表示$\small P_{j}$页面包含的超链接数,N表示所有的网页总和。由于Bingoo要对全世界的网页进行排名,所以这里的N是一个万亿级的数字。
计算开始的时候,将所有页面的PageRank值设为1,带入上面公式计算,每个页面都得到一个新的PageRank值。再把这些新的PageRank值带入上面的公式,继续得到更新的PageRank值,如此迭代计算,直到所有页面的PageRank值几乎不再有大的变化才停止。
PageRank算法我们现在看起来平平无奇,但是正是这个算法造就了Google近2万亿美元的商业帝国。在Google之前,Yahoo已经是互联网最大的搜索引擎公司。按照一般的商业规律,如果一个创新公司不能带来十倍的效率或者体验提升,就根本没有机会挑战现有的巨头。而Google刚一出现,就给Yahoo和旧有的搜索引擎世界带来摧枯拉朽的扫荡,用户体验的提升不止十倍,这其中的秘诀正是PageRank。
二十几年前,我刚刚接触编程的时候,我们中国也有很多这样的编程英雄,王选、王江民、求伯君、雷军等等,他们几乎凭一己之力就创造出一个行业。正是对这些英雄们的崇拜和敬仰,引领我在编程这条路上一直走下去。软件编程是一个可以创造奇迹的地方,而不只是为了混碗饭吃。梦想不能当饭吃,但是梦想带来的可不止是一碗饭。
PageRank的计算,需要在万亿级的数据上进行多次迭代计算才能完成。数据量和计算量都非常大,如何完成这样的计算?也就是说,具体编程实现是怎样的?
欢迎在评论区分享你的思考,我们共同进步。
评论