你好,我是陈东。
上一讲我们讲了,对于查询范围固定的应用需求,比如“查找附近的人”,我们可以根据规划好的查询区域大小,均匀划分所有的空间,然后用GeoHash将坐标转换为区域编码,以该区域编码作为Key开始检索。这样,我们就可以查到并取出该区域中的目标数据,对这些数据进行精准计算然后排序输出了。
但是,并不是所有应用的查询范围都是不变的。在一些基于地理位置的服务中,我们并不关心检索结果是否就在我们“附近”,而是必须要找到“最近”的一批满足我们要求的结果。这怎么理解呢?
我来举个例子,我们在长途自驾游的时候,突然发现车快没油了。这个时候,我们要在一个导航地图中查找最近的k个加油站给车加油,这些加油站可能并不在我们附近,但地图又必须要返回最近的k个结果。类似的情况还有很多,比如说,我们要查询最近的医院有哪些,查询最近的超市有哪些。那对于这一类的查询,如果当前范围内查不到,系统就需要自动调整查询范围,直到能返回k个结果为止。
对于这种需要动态调整范围的查询场景,我们有什么高效的检索方案呢?今天,我们就来探讨一下这个问题。
我们就以查找最近的加油站为例,一个直观的想法是,我们可以先获得当前位置的GeoHash编码,然后根据需求不停扩大查询范围进行多次查询,最后合并查询结果。这么说比较抽象,我们来分析一个具体的位置编码。
假设我们当前地址的GeoHash编码为wx4g6yc8,那我们可以先用wx4g6yc8去查找当前区域的加油站。如果查询的结果为空,我们就扩大范围。扩大查询范围的思路有两种。
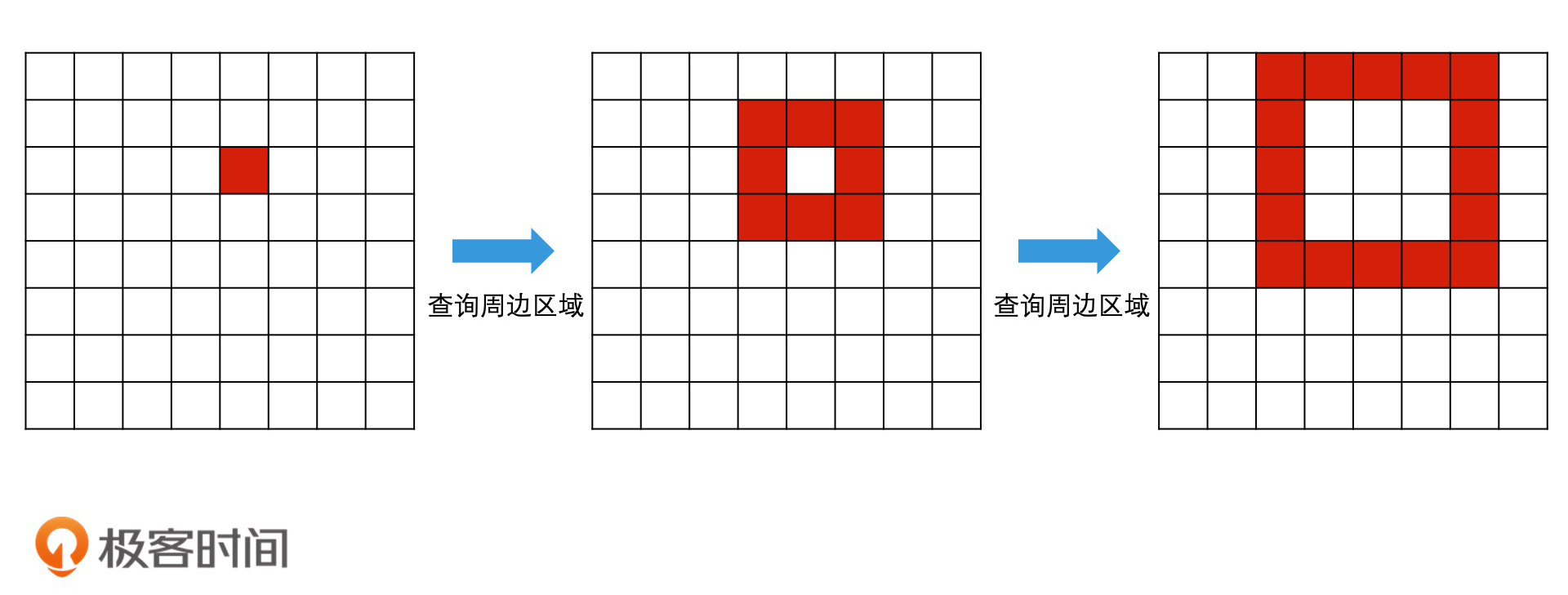
第一种思路是,一圈一圈扩大范围。具体来说就是,我们第一次查询周边8个邻接区域,如果查询结果依然为空,就再扩大一圈,查询再外圈的16个区域。如果还是不够,下一次我们就查询再外圈的24个区域,依此类推。你会发现,这种方案的查询次数会成倍地增加,它的效率并不高。

另一种思路是,我们每次都将查询单位大幅提高。比如说,直接将GeoHash编码去掉最后一位,用wx4g6yc再次去查询。如果有结果返回,但是不满足要返回Top K个的要求,那我们就继续扩大范围,再去掉一个编码,用wx4g6y去查询。就这样不停扩大单位的进行反复查询,直到结果大于k个为止。
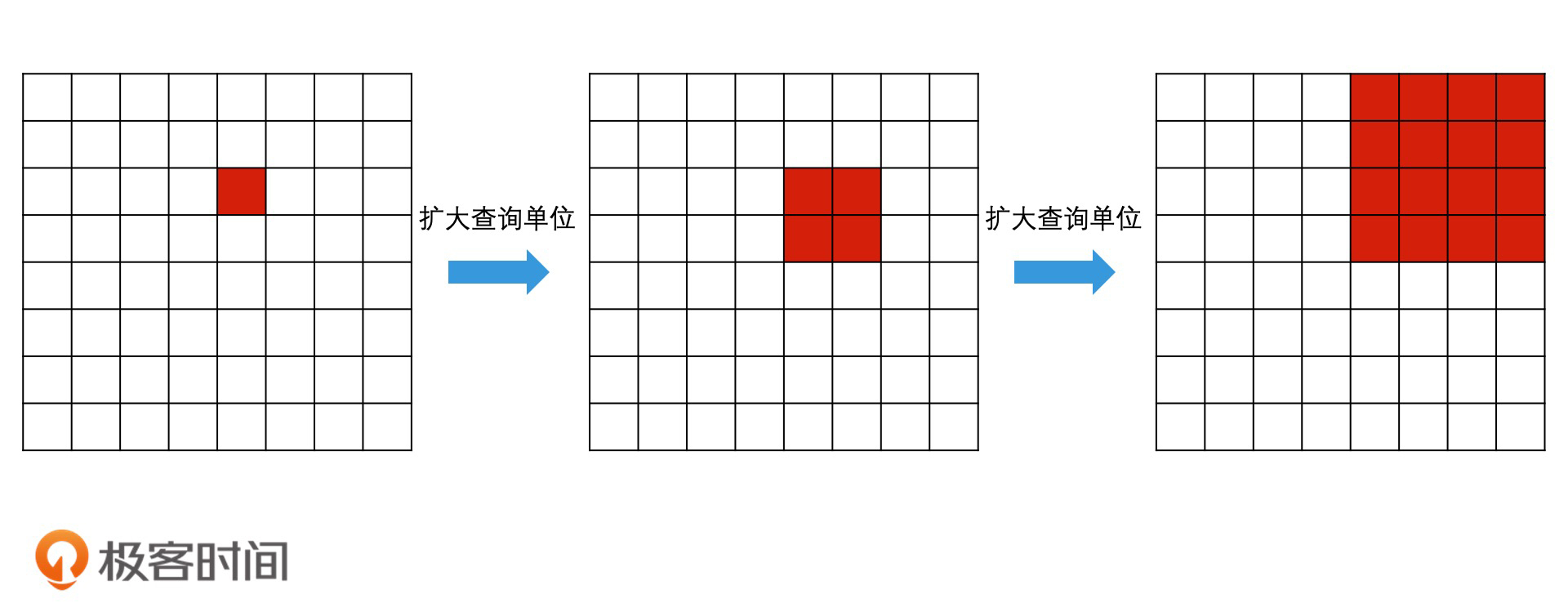
和第一种查询思路相比,在第二种思路中,我们每次查询的区域单位都得到了大范围的提升,因此,查询次数不会太多。比如说,对于一个长度为8的GeoHash编码,我们最多只需要查询8次(如果要求精准检索,那每次查询就扩展到周围8个同样大小的邻接区域即可,后面我就不再解释了)。
这个检索方案虽然用很少的次数就能“查询最近的k个结果”,但我们还需要保证,每次的查询请求都能快速返回结果。这就要求我们采用合适的索引技术,来处理GeoHash的每个层级。
比如说,如果使用基于哈希表的倒排检索来实现,我们就需要在GeoHash每个粒度层级上都分别建立一个单独的倒排表。这就意味着,每个层级的倒排表中都会出现全部的加油站,数据会被复制多次,这会带来非常大的存储开销。那我们是否有优化存储的方案呢?
我们可以利用GeoHash编码一维可排序的特点,使用数组或二叉检索树来存储和检索。由于数组和二叉检索树都可以支持范围查询,因此我们只需要建立一份粒度最细的索引就可以了。这样,当我们要检索更大范围的区域时,可以直接将原来的查询改写为范围查询。具体怎么做呢?
我来举个例子。在检索完wx4g6yc8这个区域编码以后,如果结果数量不够,还要检索wx4g6yc这个更大范围的区域编码,我们只要将查询改写为“查找区域编码在wx4g6yc0至wx4g6ycz之间的元素”,就可以利用同一个索引,来完成更高一个层级的区域查询了。同理,如果结果数量依然不够,那下一步我们就查询“区域编码在wx4g6y00至wx4g6yzz之间的元素”,依此类推。
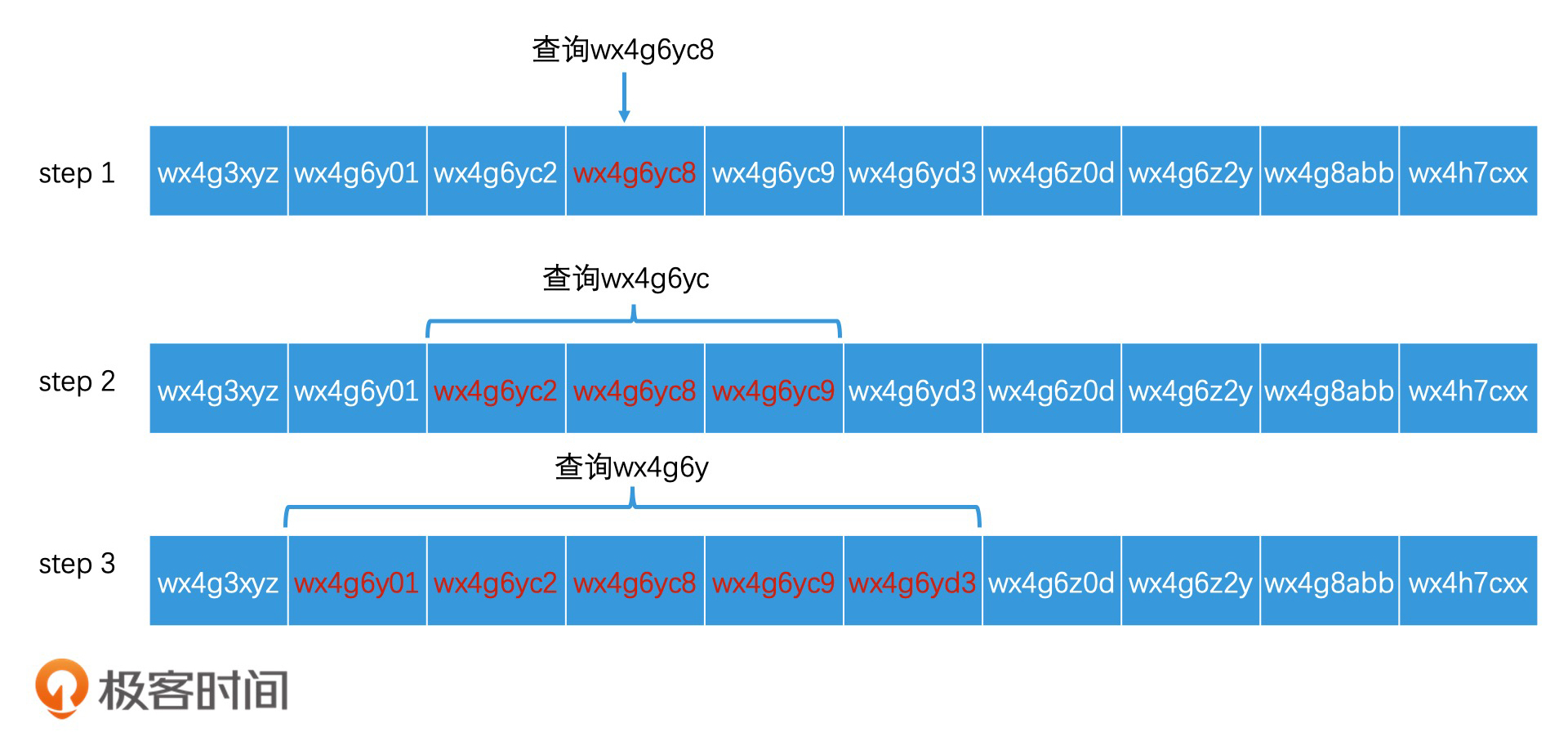
但是,这种方案有一个缺点,那就是在每次调整范围查询时,我们都要从头开始进行二分查找,不能充分利用上一次已经查询到的位置信息,这会带来无谓的重复检索的开销。那该如何优化呢?你可以先想一想,然后我们一起来看解决方案。
上一讲我们讲过,许多系统对于GeoHash的底层实现,其实都是使用二进制进行存储和计算的。而二进制区域编码的生成过程,就是一个逐渐二分空间的过程,经过二分后的区域之间是有层次关系的。如果我们把这个过程画下来,它就很像我们之前讲过的树形结构。
因此,我们可以尝试用树形结构来进行索引。这里,我们就要引入一个新的数据结构四叉树了。四叉树的树根节点代表了整个空间,每个节点的四个分叉分别表示四个子空间。其中,树根和中间节点不存储数据,只记录分叉指针。而数据只记录在最小的区域,也就是叶子节点上。
如果我们从根节点开始,不停地四分下去,直到每个分支的叶子节点都是最小粒度区域。那这样构建出来的四叉树,每个节点都有四个子节点,就叫作满四叉树。
对于满四叉树的每个节点,我们都可以编号。换句话说,我们可以按00、01、10、11的编号,来区分满四叉树的四个子节点。这样一来,只要我们从根节点遍历到叶子节点,然后将路径上每个节点的编号连起来,那最后得到的编码就是这个叶子节点所代表的区域编码。
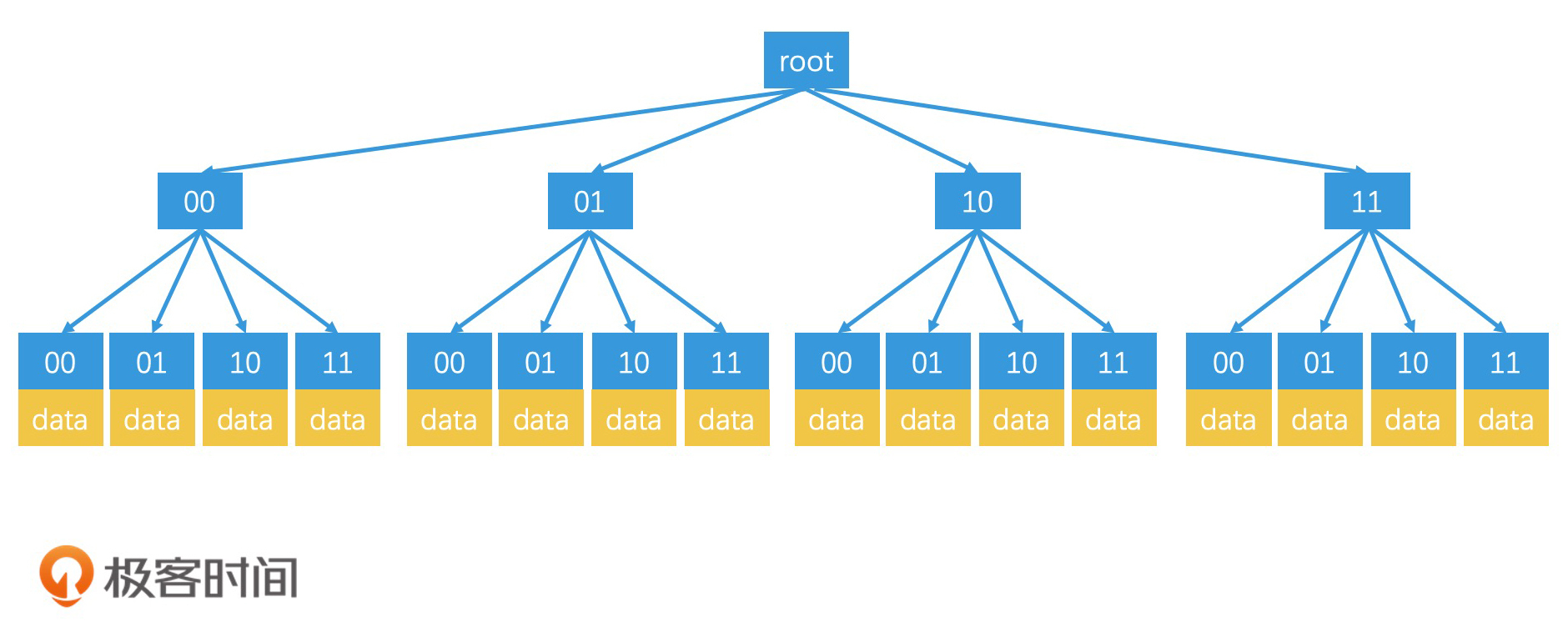
好了,现在我们知道了四叉树的结构和特点了,那我们怎么利用它完成自动调整范围的Top K检索呢?下面,我们通过一个例子来看看。
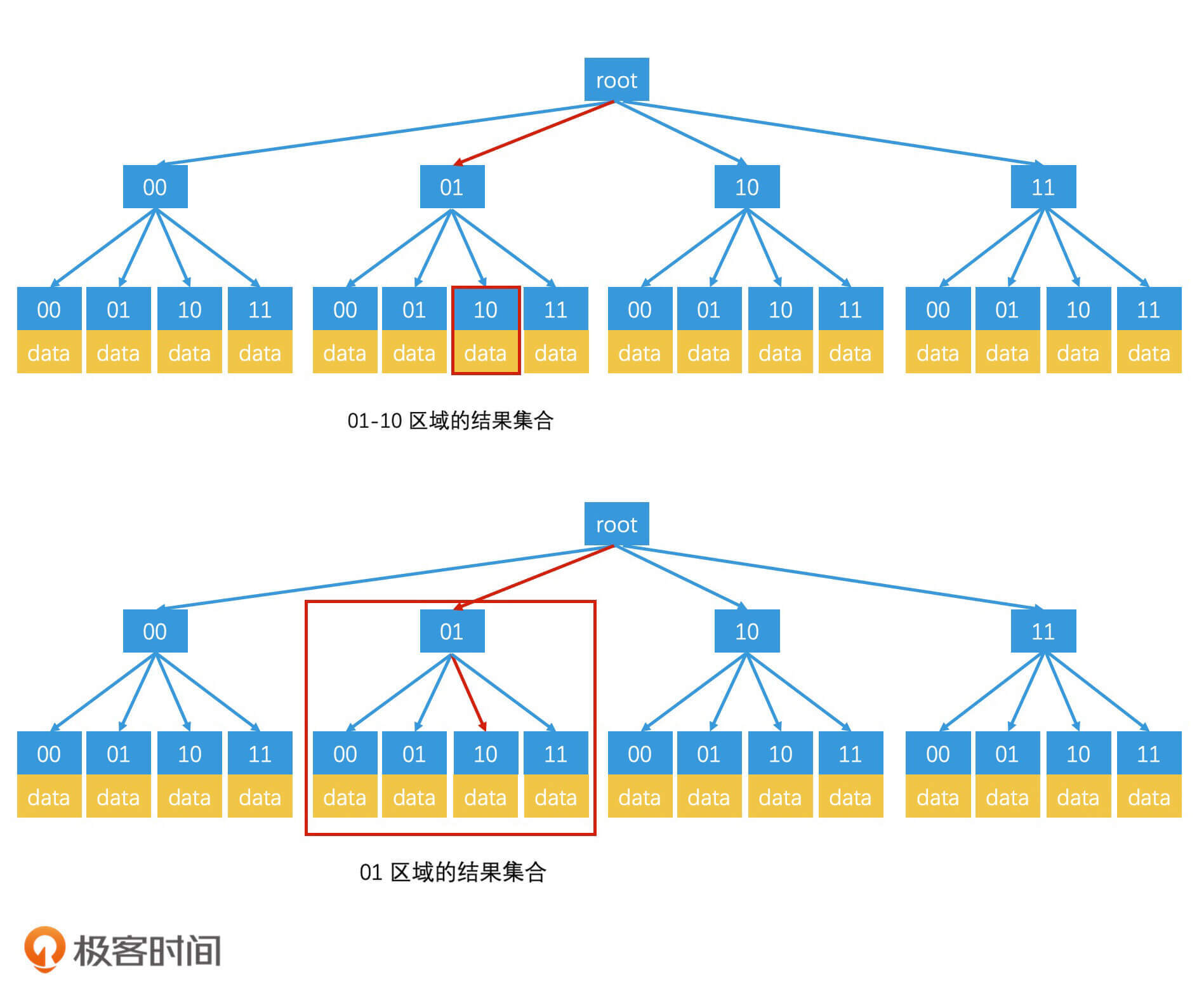
假设一个人所属的最小区域编码是0110,那我们在检索的时候,就以0110为Key,沿着四叉树的对应分支去寻找相应的区域,查询路径为01-10。如果查找到了叶子节点,并且返回的结果大于k个,就可以直接结束检索。如果返回结果不足k个,我们就得递归返回到上一层的父节点,然后以这整个父节点的区域编码为目标进行检索。这样,我们就避免了要再次从树根检索到父节点的开销,从而提升了检索效率。
尽管,我们使用以最小区域单位为叶子节点的满四叉树,能够很好的提升检索效率,但是在数据稀疏的时候,许多叶子节点中的数据可能是空的,这就很有可能造成大量的空间浪费。为了避免出现空间浪费,我们有一种改进方案是,使用动态节点分裂的非满四叉树。
首先,我们可以给每个叶子节点规定一个容纳上限。比如说,我们可以将上限设置为n。那么,一开始的四叉树只有一个根节点,这个根节点同时也是叶子节点,它表明了当前的全部空间范围。当有数据加入的时候,我们直接记录在这个节点中,查询时也只查询这个节点即可。因此,当插入的数据个数小于n时,我们不需要进行任何复杂的查找操作,只需要将根节点的所有数据读出,然后进行距离计算并排序即可。
随着加入的数据越来越多,如果一个叶子节点的容量超出了容纳上限,我们就将该节点进行分裂。首先,我们将该节点转为中间节点,然后,我们会为这个节点生成1至4个叶子节点(注意:不是一定要生成4个叶子节点),并将原来存在这个节点上的数据都转入到对应的叶子节点中。这样,我们就完成了分裂。
不过,有一种极端的情况是,这些数据都会转入到同一个下层叶子节点上。这时,我们就需要继续分裂这个叶子节点,直到每个叶子节点的容量在阈值下为止。
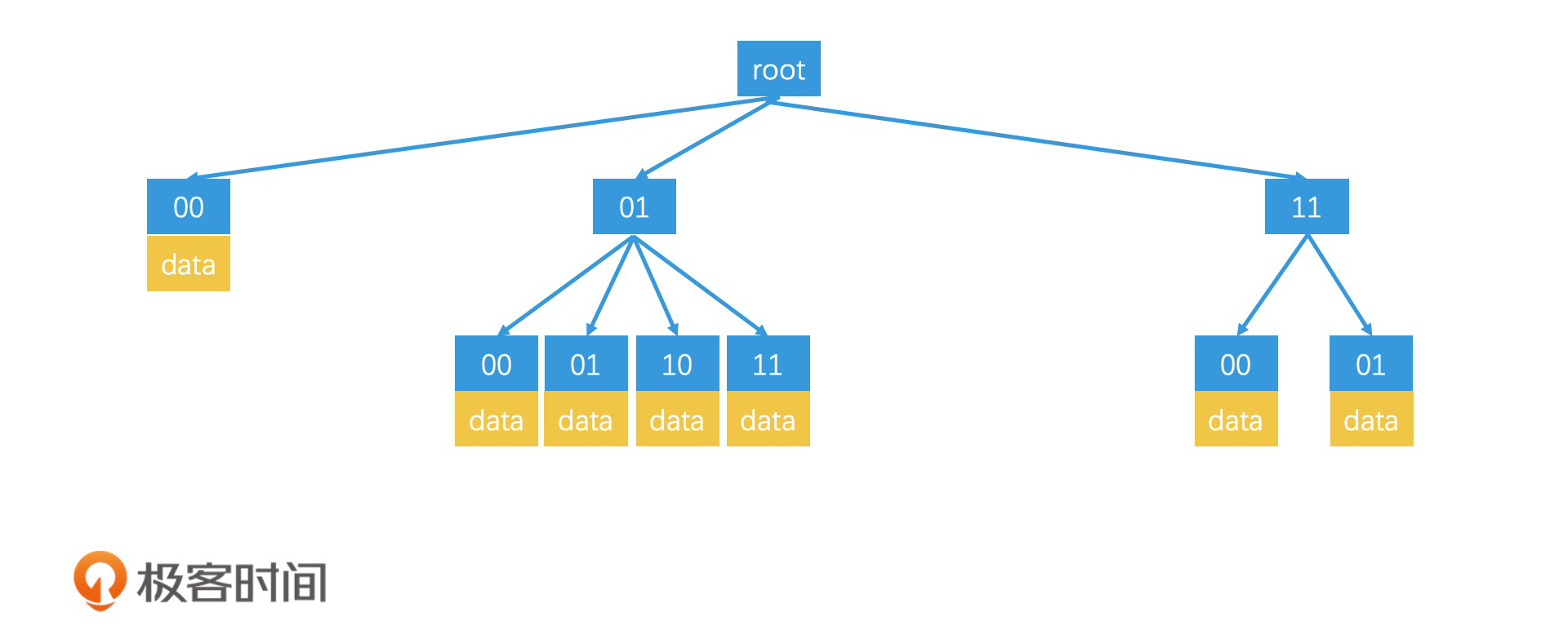
通过这种动态生成叶节点的方案,我们就能得到一棵非满四叉树。和满四叉树相比,它的叶子节点会更少,而且每个叶子节点表示的区域范围也可能是不一样的。这使得非满四叉树具有更好的空间利用率。非满四叉树的查询过程和满四叉树十分相似,也是根据当前的区域编码,找到对应的叶子节点,并根据该叶子节点上存储的数据数量,判断是否要递归扩大范围。这里我就不再详细说了。
上面,我们都是用二进制编码来说明的。你可能会问,如果我们使用了GeoHash编码方式,是否也可以用类似的检索技术来索引呢?当然是可以的。实际上,对于字符串的检索,有一种专门的数据结构,叫作前缀树(Trie树)。
前缀树的思路和四叉树非常相似,它也是一种逐层划分检索空间的数据结构。它的根节点代表了整个检索空间,然后每个中间节点和叶子节点都只存储一个字符,代表一个分支。这样,从根节点到叶子节点的路径连起来,就是一个完整的字符串。因此,当使用GeoHash编码来表示区域时,我们可以建立一个前缀树来进行索引,前缀树的每个节点最多会有32个子节点。
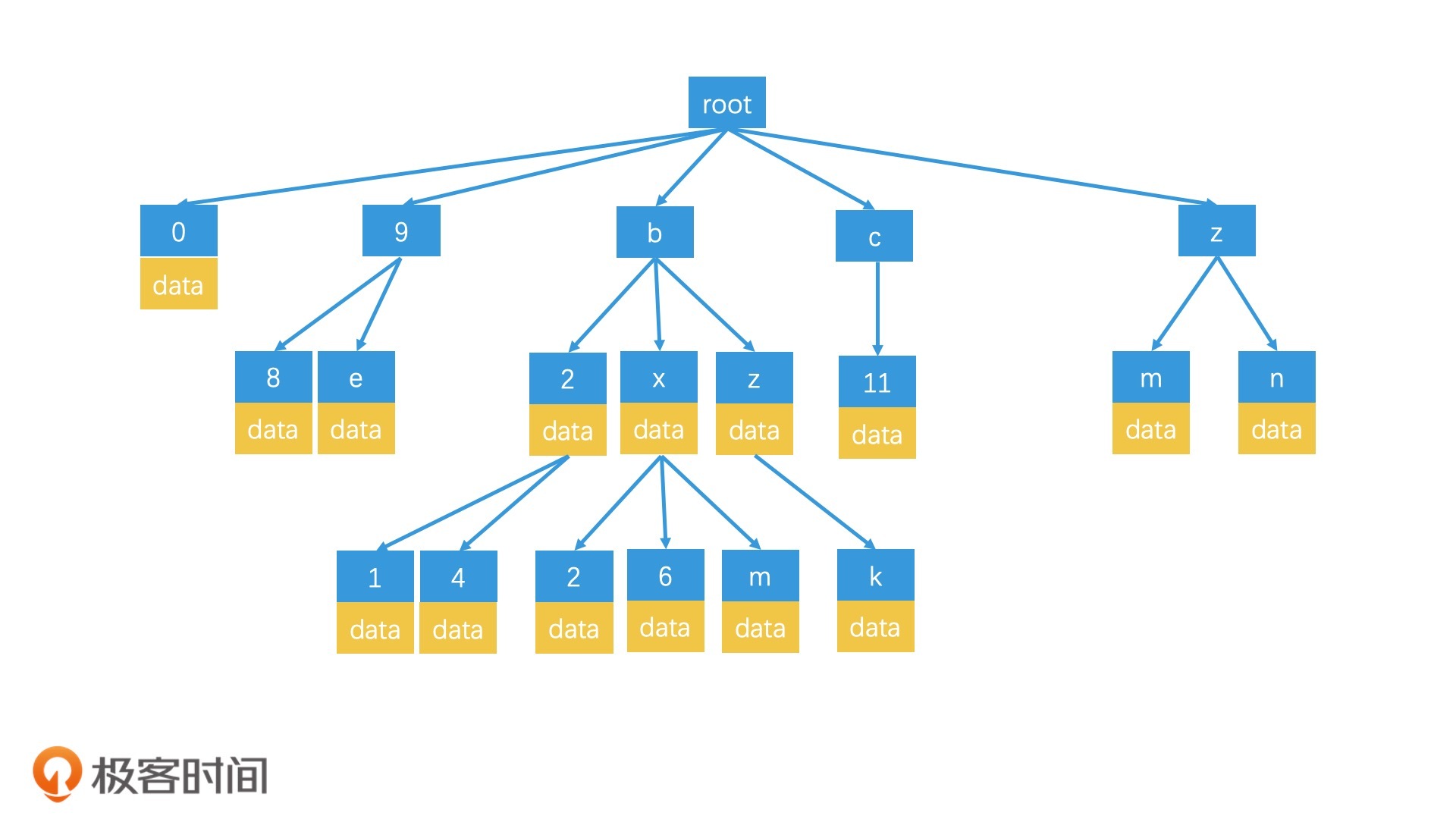
那如何利用前缀树来检索呢?举个例子,当我们查询wx4g6yc8这个区域时,我们会沿着w-x-4-g-6-y-c-8的路径,检索到对应的叶子节点,然后取出这个叶子节点上存储的数据。如果这个区域的数据不足k个,就返回到父节点上,检索对应的区域,直到返回结果达到k个为止。由于整体思路和四叉树是十分相似的,这里就不展开细说了。
此外,前缀树除了用在GeoHash编码的检索上,也经常用于字典的检索,因此也叫字典树。字典树适用于匹配字符串的检索场合。
总结来说,利用树形结构来划分空间提高检索效率的方案,它的应用非常广泛。对于更高维度空间的最近邻检索,我们也可以使用类似的检索方案来划分空间。比如说,在三维空间中,八叉树就是常见的检索方案。那拓展到更高的维度,如k维,我们还可以使用k-d树(K-Dimensional Tree)来检索。
k-d树一种是更通用的,对任意维度都可以使用的检索方案。k-d树和四叉树、八叉树的检索思路并不相同,它在划分子空间的时候,并不是直接将整个空间划分为2^k个子空间,而是会选出最有区分度的一个维度,将该维度的空间进行二分,然后对划分出的子空间再进行同样的二分处理,所以,它实际上是一个二叉树。而且,由于它的分支数和维度k的具体值无关,因此具有更好的通用性。
事实上,k-d树在维度规模不大的场景下,确实具有不错的检索效率。但是,在成百上千的超高维度的场景中,k-d树的性能会急剧下降。那在高维空间中,我们又该如何快速地查找到最近的k个对象呢?这个问题,也是搜索引擎和推荐引擎在很多应用场景中都要解决问题。在后面两讲中,我们会对它作详细讲解。
今天,我们重点学习了,在二维空间中利用四叉树,来快速寻找最近的k个元素的方法。
在需要动态调整查询范围的场景下,对于二进制编码的二维空间的最近邻检索问题,我们可以通过四叉树来完成。四叉树可以很好地快速划分查询空间,并通过递归的方式高效地扩大查询范围。但是满四叉树经常会造成无谓的空间浪费,为了避免这个问题,在实际应用的时候,我们会选择使用非满四叉树来存储和索引编码。对于GeoHash编码的二维空间最近邻检索问题,我们也能通过类似的前缀树来提高检索效率。
在非满四叉树的分裂过程中,为什么一个节点不一定会生成4个叶子节点?你能举一个例子吗?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这一讲分享给你的朋友。
评论