
讲完校验码之后,你现在应该知道,无论是奇偶校验码,还是CRC这样的循环校验码,都只能告诉我们一个事情,就是你的数据出错了。所以,校验码也被称为检错码(Error Detecting Code)。
不管是校验码,还是检错码,在硬件出错的时候,只能告诉你“我错了”。但是,下一个问题,“错哪儿了”,它是回答不了的。这就导致,我们的处理方式只有一种,那就是当成“哪儿都错了”。如果是下载一个文件,发现校验码不匹配,我们只能重新去下载;如果是程序计算后放到内存里面的数据,我们只能再重新算一遍。
这样的效率实在是太低了,所以我们需要有一个办法,不仅告诉我们“我错了”,还能告诉我们“错哪儿了”。于是,计算机科学家们就发明了纠错码。纠错码需要更多的冗余信息,通过这些冗余信息,我们不仅可以知道哪里的数据错了,还能直接把数据给改对。这个是不是听起来很神奇?接下来就让我们一起来看一看。
最知名的纠错码就是海明码。海明码(Hamming Code)是以他的发明人Richard Hamming(理查德·海明)的名字命名的。这个编码方式早在上世纪四十年代就被发明出来了。而直到今天,我们上一讲所说到的ECC内存,也还在使用海明码来纠错。
最基础的海明码叫7-4海明码。这里的“7”指的是实际有效的数据,一共是7位(Bit)。而这里的“4”,指的是我们额外存储了4位数据,用来纠错。
首先,你要明白一点,纠错码的纠错能力是有限的。不是说不管错了多少位,我们都能给纠正过来。不然我们就不需要那7个数据位,只需要那4个校验位就好了,这意味着我们可以不用数据位就能传输信息了。这就不科学了。事实上,在7-4海明码里面,我们只能纠正某1位的错误。这是怎么做到的呢?我们一起来看看。
4位的校验码,一共可以表示 2^4 = 16 个不同的数。根据数据位计算出来的校验值,一定是确定的。所以,如果数据位出错了,计算出来的校验码,一定和确定的那个校验码不同。那可能的值,就是在 2^4 - 1 = 15 那剩下的15个可能的校验值当中。
15个可能的校验值,其实可以对应15个可能出错的位。这个时候你可能就会问了,既然我们的数据位只有7位,那为什么我们要用4位的校验码呢?用3位不就够了吗?2^3 - 1 = 7,正好能够对上7个不同的数据位啊!
你别忘了,单比特翻转的错误,不仅可能出现在数据位,也有可能出现在校验位。校验位本身也是可能出错的。所以,7位数据位和3位校验位,如果只有单比特出错,可能出错的位数就是10位,2^3 - 1 = 7 种情况是不能帮我们找到具体是哪一位出错的。
事实上,如果我们的数据位有K位,校验位有N位。那么我们需要满足下面这个不等式,才能确保我们能够对单比特翻转的数据纠错。这个不等式就是:
在有7位数据位,也就是K=7的情况下,N的最小值就是4。4位校验位,其实最多可以支持到11位数据位。我在下面列了一个简单的数据位数和校验位数的对照表,你可以自己算一算,理解一下上面的公式。

现在你应该搞清楚了,在数据位数确定的情况下,怎么计算需要的校验位。那接下来,我们就一起看看海明码的编码方式是怎么样的。
为了算起来简单一点,我们少用一些位数,来算一个4-3海明码(也就是4位数据位,3位校验位)。我们把4位数据位,分别记作d1、d2、d3、d4。这里的d,取的是数据位data bits的首字母。我们把3位校验位,分别记作p1、p2、p3。这里的p,取的是校验位parity bits的首字母。
从4位的数据位里面,我们拿走1位,然后计算出一个对应的校验位。这个校验位的计算用之前讲过的奇偶校验就可以了。比如,我们用d1、d2、d4来计算出一个校验位p1;用d1、d3、d4计算出一个校验位p2;用d2、d3、d4计算出一个校验位p3。就像下面这个对应的表格一样:
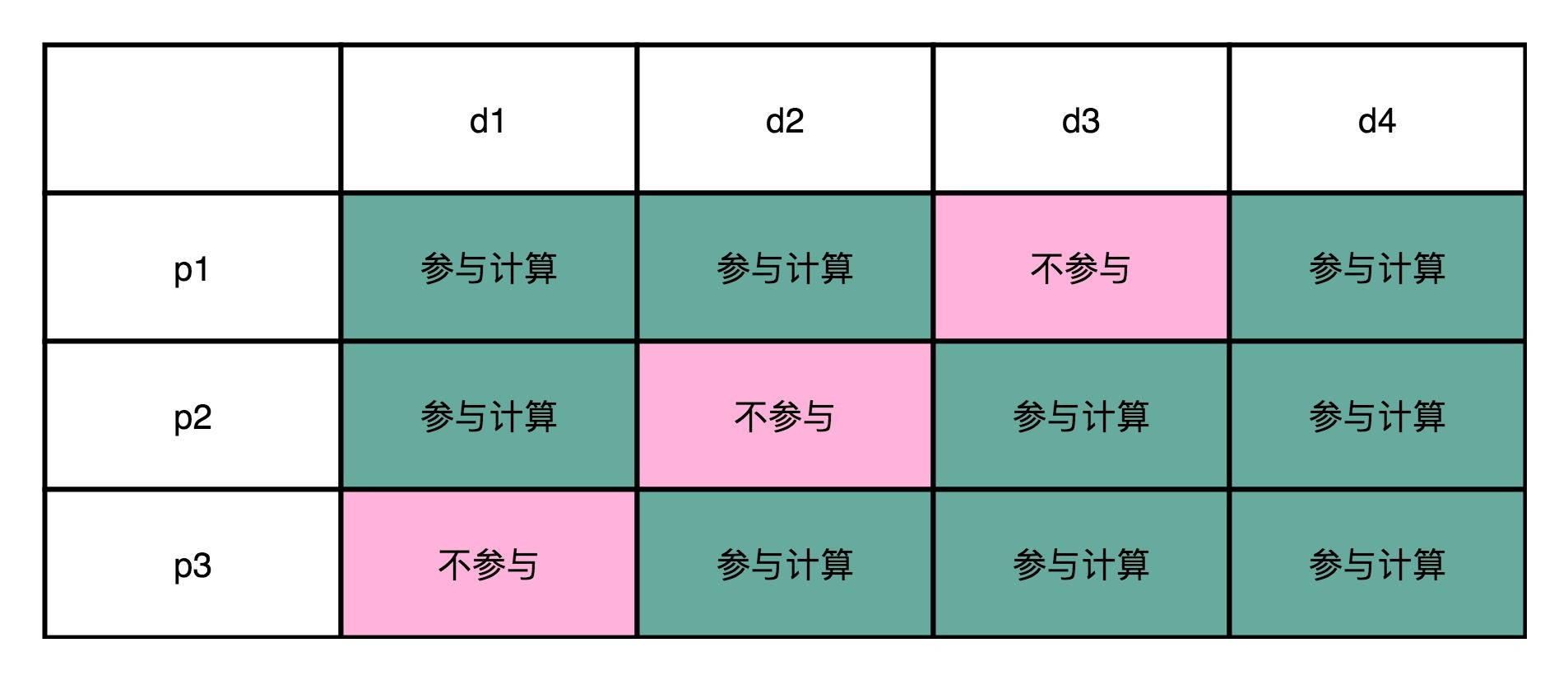
这个时候,你去想一想,如果d1这一位的数据出错了,会发生什么情况?我们会发现,p1和p2和校验的计算结果不一样。d2出错了,是因为p1和p3的校验的计算结果不一样;d3出错了,则是因为p2和p3;如果d4出错了,则是p1、p2、p3都不一样。你会发现,当数据码出错的时候,至少会有2位校验码的计算是不一致的。
那我们倒过来,如果是p1的校验码出错了,会发生什么情况呢?这个时候,只有p1的校验结果出错。p2和p3的出错的结果也是一样的,只有一个校验码的计算是不一致的。
所以校验码不一致,一共有 2^3-1=7种情况,正好对应了7个不同的位数的错误。我把这个对应表格也放在下面了,你可以理解一下。
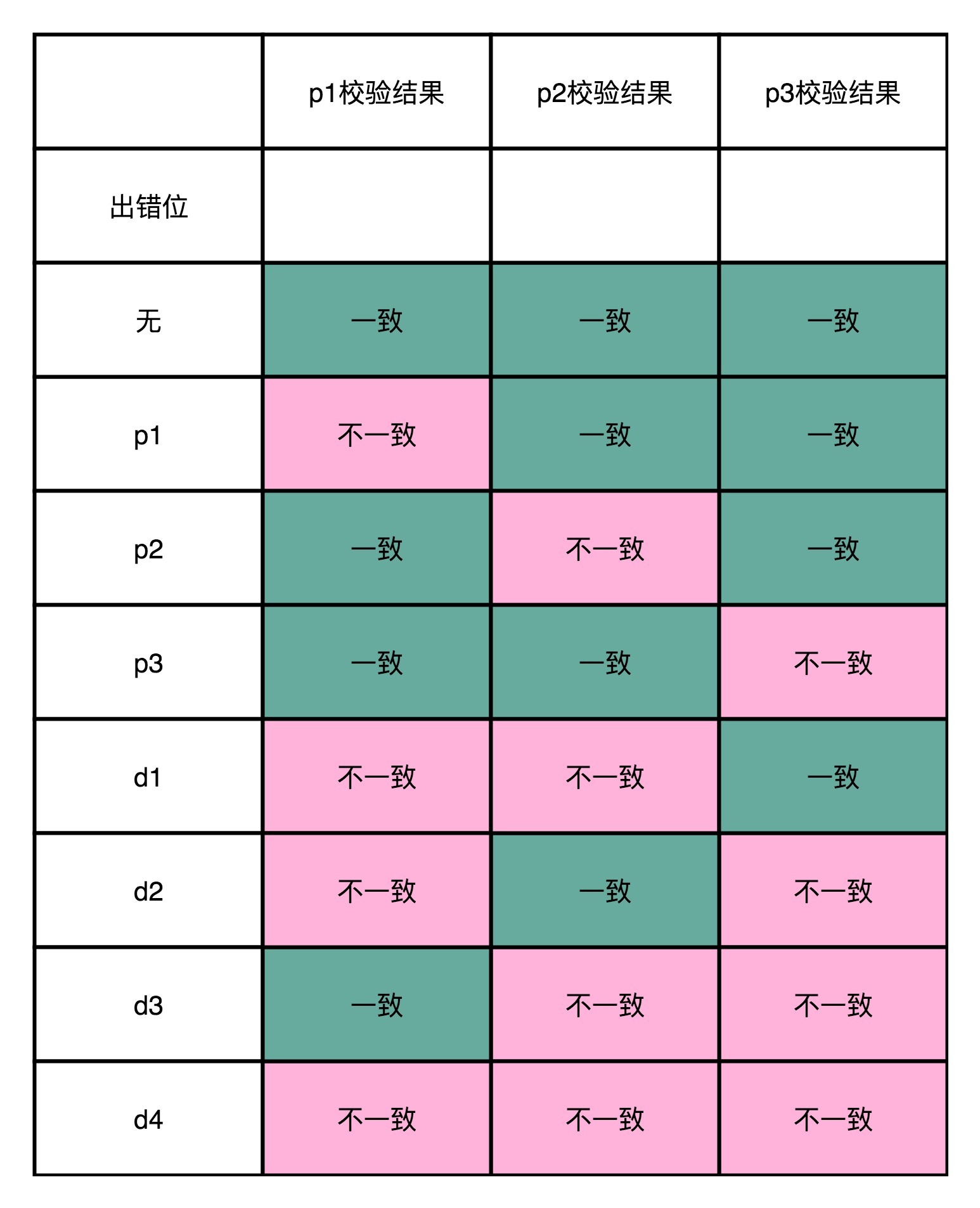
可以看到,海明码这样的纠错过程,有点儿像电影里面看到的推理探案的过程。通过出错现场的额外信息,一步一步条分缕析地找出,到底是哪一位的数据出错,还原出错时候的“犯罪现场”。
看到这里,相信你一方面会觉得海明码特别神奇,但是同时也会冒出一个新的疑问,我们怎么才能用一套程序或者规则来生成海明码呢?其实这个步骤并不复杂,接下来我们就一起来看一下。
首先,我们先确定编码后,要传输的数据是多少位。比如说,我们这里的7-4海明码,就是一共11位。
然后,我们给这11位数据从左到右进行编号,并且也把它们的二进制表示写出来。
接着,我们先把这11个数据中的二进制的整数次幂找出来。在这个7-4海明码里面,就是1、2、4、8。这些数,就是我们的校验码位,我们把他们记录做p1~p4。如果从二进制的角度看,它们是这11个数当中,唯四的,在4个比特里面只有一个比特是1的数值。
那么剩下的7个数,就是我们d1-d7的数据码位了。
然后,对于我们的校验码位,我们还是用奇偶校验码。但是每一个校验码位,不是用所有的7位数据来计算校验码。而是p1用3、5、7、9、11来计算。也就是,在二进制表示下,从右往左数的第一位比特是1的情况下,用p1作为校验码。
剩下的p2,我们用3、6、10、11来计算校验码,也就是在二进制表示下,从右往左数的第二位比特是1的情况下,用p2。那么,p3自然是从右往左数,第三位比特是1的情况下的数字校验码。而p4则是第四位比特是1的情况下的校验码。
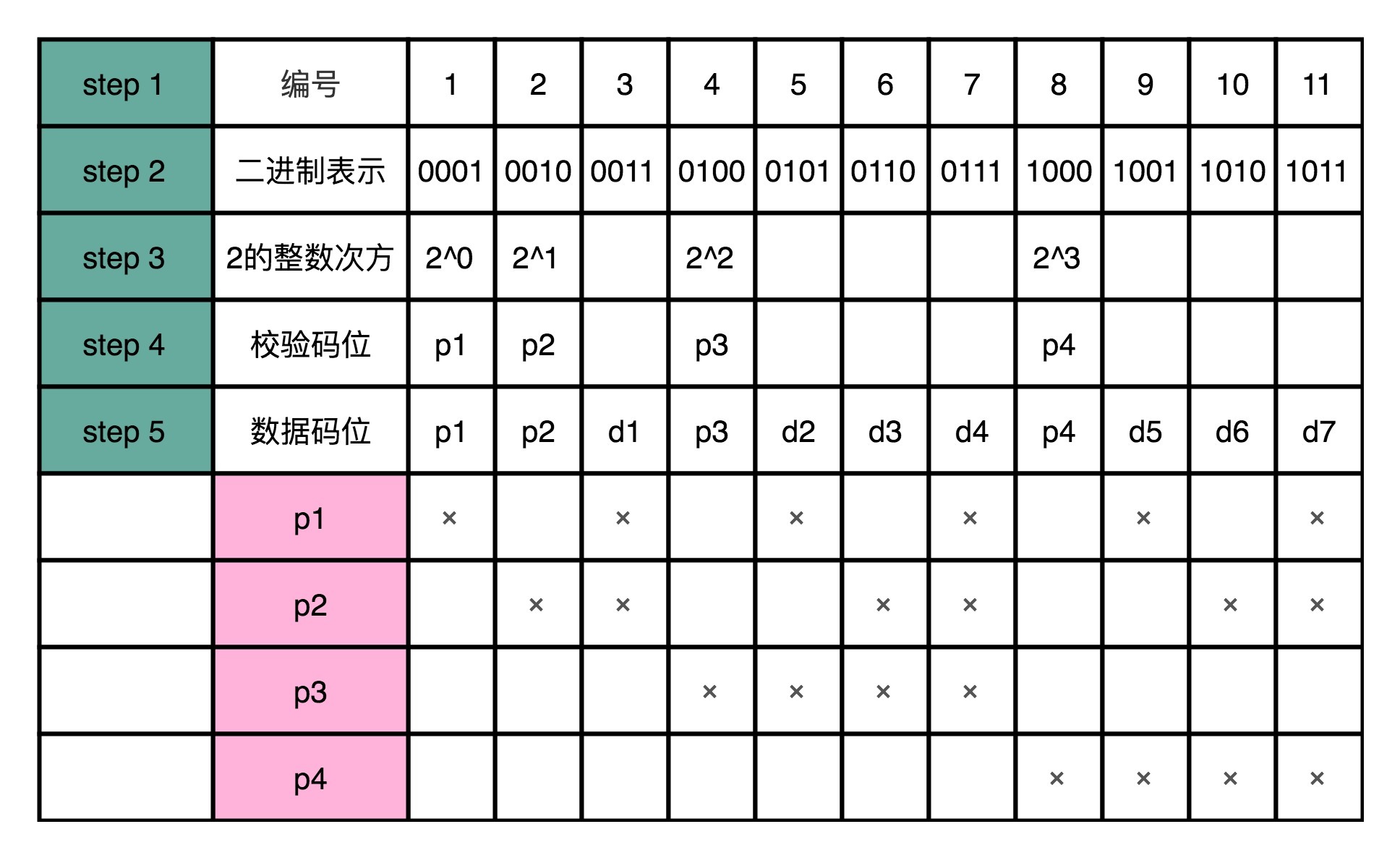
这个时候,你会发现,任何一个数据码出错了,就至少会有对应的两个或者三个校验码对不上,这样我们就能反过来找到是哪一个数据码出错了。如果校验码出错了,那么只有校验码这一位对不上,我们就知道是这个校验码出错了。
上面这个方法,我们可以用一段确定的程序表示出来,意味着无论是几位的海明码,我们都不再需要人工去精巧地设计编码方案了。
其实,我们还可以换一个角度来理解海明码的作用。对于两个二进制表示的数据,他们之间有差异的位数,我们称之为海明距离。比如 1001 和 0001 的海明距离是1,因为他们只有最左侧的第一位是不同的。而1001 和 0000 的海明距离是2,因为他们最左侧和最右侧有两位是不同的。
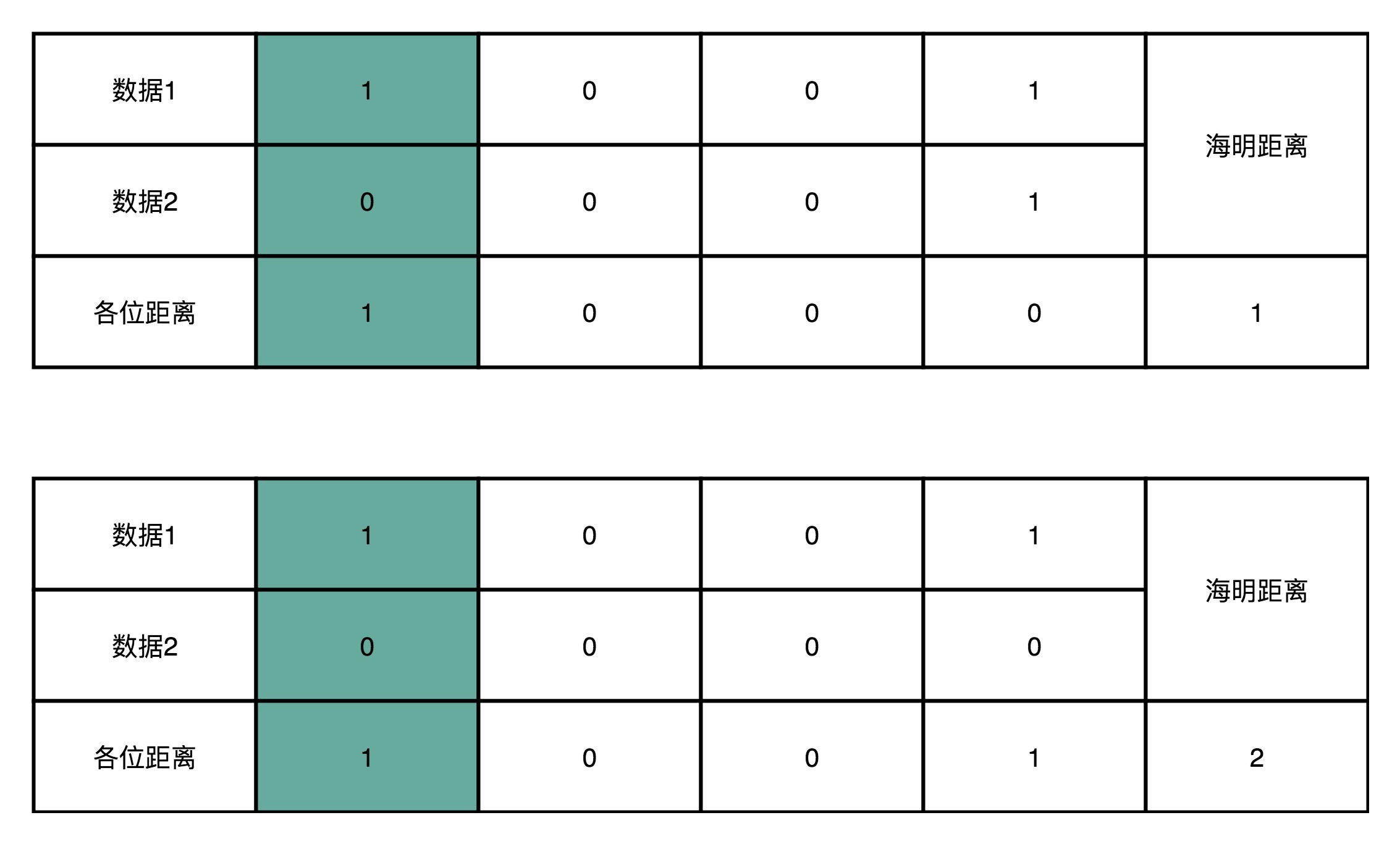
于是,你很容易可以想到,所谓的进行一位纠错,也就是所有和我们要传输的数据的海明距离为1的数,都能被纠正回来。
而任何两个实际我们想要传输的数据,海明距离都至少要是3。你可能会问了,为什么不能是2呢?因为如果是2的话,那么就会有一个出错的数,到两个正确的数据的海明距离都是1。当我们看到这个出错的数的时候,我们就不知道究竟应该纠正到那一个数了。
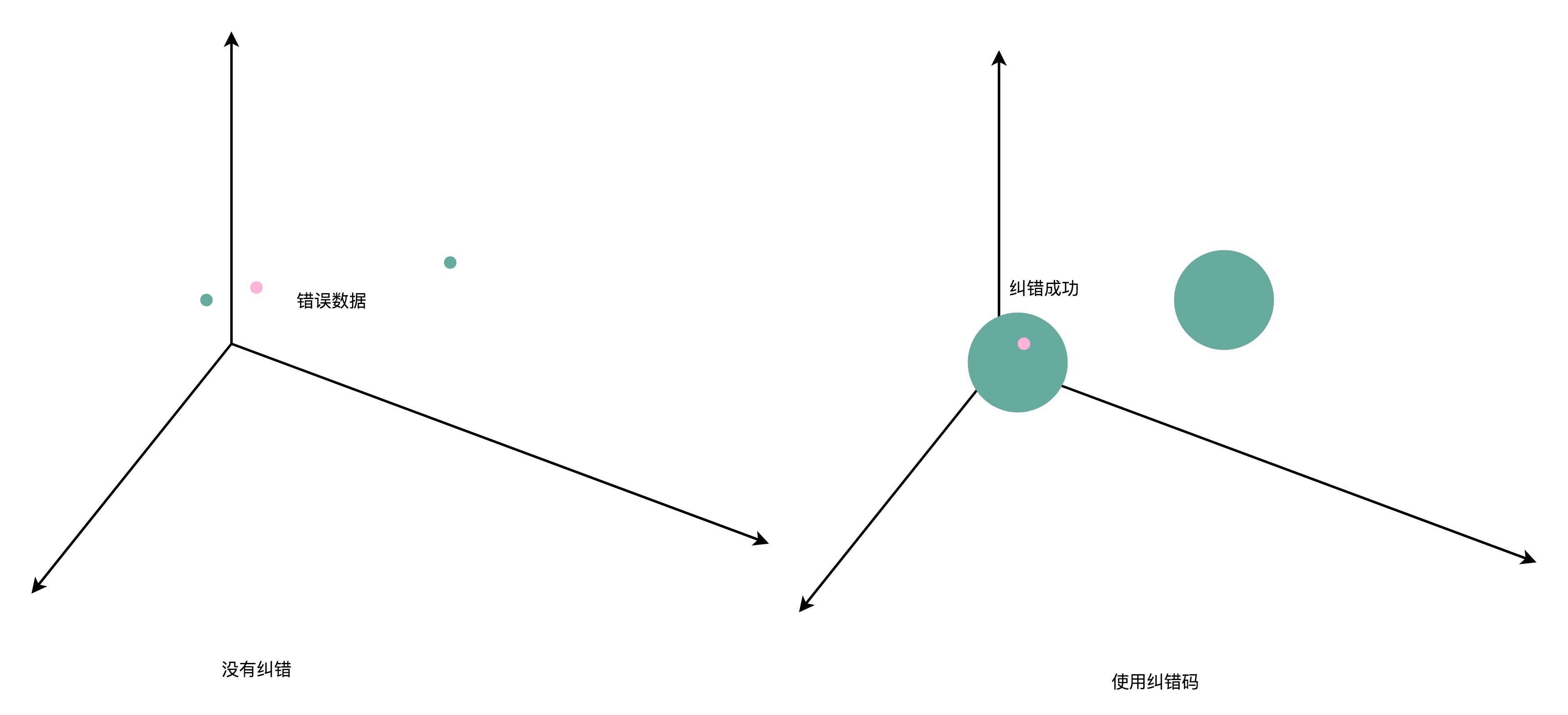
在引入了海明距离之后,我们就可以更形象地理解纠错码了。在没有纠错功能的情况下,我们看到的数据就好像是空间里面的一个一个点。这个时候,我们可以让数据之间的距离很紧凑,但是如果这些点的坐标稍稍有错,我们就可能搞错是哪一个点。
在有了1位纠错功能之后,就好像我们把一个点变成了以这个点为中心,半径为1的球。只要坐标在这个球的范围之内,我们都知道实际要的数据就是球心的坐标。而各个数据球不能距离太近,不同的数据球之间要有3个单位的距离。
好了,纠错码的内容到这里就讲完了。你可不要小看这个看起来简单的海明码。虽然它在上世纪40年代早早地就诞生了,不过直到今天的ECC内存里面,我们还在使用这个技术方案。而海明也因为海明码获得了图灵奖。
通过在数据中添加多个冗余的校验码位,海明码不仅能够检测到数据中的错误,还能够在只有单个位的数据出错的时候,把错误的一位纠正过来。在理解和计算海明码的过程中,有一个很重要的点,就是不仅原来的数据位可能出错。我们新添加的校验位,一样可能会出现单比特翻转的错误。这也是为什么,7位数据位用3位校验码位是不够的,而需要4位校验码位。
实际的海明码编码的过程也并不复杂,我们通过用不同过的校验位,去匹配多个不同的数据组,确保任何一个数据位出错,都会产生一个多个校验码位出错的唯一组合。这样,在出错的时候,我们就可以反过来找到出错的数据位,并纠正过来。当只有一个校验码位出错的时候,我们就知道实际出错的是校验码位了。
这一讲的推荐阅读,还是让我们回到教科书。我推荐你去读一读《计算机组成与设计:软件/硬件接口》的5.5章节,关于可信存储器的部分。
另外,如果你想在纠错码上进一步深入,你可以去了解一下纠删码,也就是Erasure Code。最好的学习入口当然还是Wikipedia。
7明码,除了可以进行单个位的纠错之外。还能做到可以检测(Detection)到两个位的出错。也就是说,虽然我们不知道是哪两个比特错了,但是我们还是知道数据是错了的。为什么能够做到这一点呢?
你可以好好思考一下,然后在留言区写下你的答案。如果有收获,你也可以把这篇文章分享给你的朋友。
评论