你好，我是海纳。

上节课，我整体介绍了编译过程包含的几个基本步骤：预处理、词法分析、文法分析、语义分析、中间表示的优化，以及目标文件生成等。然后，我又重点介绍了预处理和词法分析。那按照先后顺序，这节课我们继续来看文法分析。

文法分析技术不只用于编译器中，在JSON文件解析、XML文件解析等场景中也被广泛地使用，它其实是一种处理格式化文本的技术。所以学习这节课，你要掌握的不仅是文法分析的具体技术，更重要的是要理解它处理格式化文本的原理。只有深刻地理解了原理，我们才能做到在具体的场景中，根据需要自由地修改算法的实现。

接下来，我们就具体看看文法分析吧。

文法分析

文法，或者叫语法（Grammar），它描述了一套语言的产生规则。例如，一个合法的句子包含主语、谓语和宾语。那么，我们就可以这样定义句子的规则：

$Sent\rightarrow S P O$

其中，Sent代表一个句子，S代表主语（Subject），P代表谓语（Predicate），O代表宾语（Object）。上述公式可以这么理解：句子可以推导成主语加谓语加宾语的结构。

主语则可以进一步定义成具体的人。例如，Tom或者Mary，这个定义也可以使用一个公式来表示：

$S\rightarrow Tom | Mary$

也就是说，主语S可以继续推导，但Tom或者Mary则不能再继续推导下去了。这样，人们就把可以推导下去的符号称为非终结符，例如Sent、S都是非终结符，P和O当然也是非终结符；同时把不可以继续推导的符号称为终结符，例如Mary和Tom。

谓语和宾语也有对应的推导规则，举例来说：

$P \rightarrow play | eat$

$O\rightarrow basketball | apple$

这样的四条规则就组成了一个关于句子的文法。如果我们遇到句子“Tom plays basketball”，就可以反向使用规则，对这个句子进行分析。正向使用规则叫作推导，而反向使用规则被称为归约。我们看到Tom可以归约为S，play可以归约为P，basketball可以规约为O，所以上述句子经过第一层规约就变成了“SPO”。而这可以继续反向使用第一条规则，将其归约为Sent，也就是说这是一个合乎文法的句子。换句话说，句子“Tom plays basketball”被文法Sent接受了。

编程语言的解析也借助了文法这个概念。我们对源文件进行文法分析的过程，其实就是使用文法对源文件进行归约的过程。如果能归约到顶级规则，那就说明源文件是没有文法错误的，否则就应该报源文件有语法错误。

将源代码归约到顶级规则的手段，是一种自底向上的分析手段，它使用文法规则的时候是从右向左进行归约的。人们称这种分析方式为LR算法，其中的L代表源文件的分析方向是从左向右的，而R则代表规则的使用方向是从右向左的，或者说自底向上的。

很多自动化文法分析工具，例如yacc、javacc等，都是基于LR算法来进行文法分析的。这些工具为开发新的语言提供了便利。但实际上，近二十年来新出现的编程语言却越来越喜欢使用另外一种自顶向下的分析方法，它也叫作递归下降的分析方式。自顶向下的分析方法具有简洁直观的优点，代码易读易维护，深受编译器开发人员的喜爱。所以这节课，我就重点介绍递归下降的自顶向下的分析方法。

自顶向下的分析方法

自顶向下的分析方法，其特点是从顶层规则的最左侧的符号开始，尝试不断地使用文法中的各种规则，对输入字符串进行匹配。

而具体做法是将非终结符实现为函数，在函数中对终结符进行匹配。这里，我用表达式求值的程序来进行说明。一个表达式的文法规则可以这样定义：

$expr \rightarrow term([+|-] term)*$

$term \rightarrow factor([*|/]) factor) *$

$factor \rightarrow NUM| (expr)$

顶级规则是expr，这条规则代表表达式的定义，一个表达式可以是多项式的一个项或者多个项的和或者差。

第二条规则是项的规则，一个项可以是一个因子，或者多个因子的积或者商。这条规则保证了乘除法的优先级高于加减法。

第三条规则是因子的规则，它可以是一个整数，或者是用括号括起来的表达式。这就定义了括号的优先级是最高的。

接下来，我分步骤来讲解文法分析的过程。

第一步，先扩展词法分析器，让它可以支持小括号、加减符号和乘除符号。这一段的核心逻辑在上一节课中已经讲过了，这里就不再赘述。完整的代码我已经放在了gitee上，请你自己去查看词法分析的代码。

第二步，定义文法分析器，将非终结符翻译成函数。表达式的文法里有三个非终结符，分别是 expr、term和factor，所以我们就定义三个函数，代码如下：

/* 表达式规则的文法解析过程 */
int expr() {
    int a = 0, b = 0;
    a = term(); /* 一个表达式最少包含一项 */

    while (t->_type == TT_ADD || t->_type == TT_SUB) {
        if (t->_type == TT_ADD) {
            t = next_token();
            b = term();
            a += b;
        }
        else if (t->_type == TT_SUB) {
            t = next_token();
            b = term();
            a -= b;
        }
    }

    return a;
}

/* 每一项的文法分析过程 */
int term() {
    int a = 0, b = 0;
    a = factor(); /* 最少包含一个因子 */

    while (t->_type == TT_MUL || t->_type == TT_DIV) {
        if (t->_type == TT_MUL) {
            t = next_token();
            b = factor();
            a *= b;
        }
        else if (t->_type == TT_DIV) {
            t = next_token();
            b = factor();
            a /= b;
        }
    }

    return a;
}

int factor() {
    if (t->_type == TT_INTEGER) { /* 可以是一个整数 */
        int a = t->_value._int;
        t = next_token();
        return a;
    }
    else if (t->_type == TT_LEFT_PAR) { /* 或者是括号里的表达式 */
        t = next_token();
        int a = expr();
        if (!match(TT_RIGHT_PAR)) /* 不要忘了还有一个右括号 */
            return 0;
        else
            return a;
    }
    else {
        printf("Parse Error\n");
        return 0;
    }
}

其中，函数expr对应expr规则，函数term对应term规则，而函数factor对应factor规则。在对应的时候，或结构（中括号和竖线表示或）就会被翻译成if…else语句，而有零个或者多个（用*表示）就会被翻译成while语句。这种对应规则是非常简明的，只要你仔细对照体会，就能明白为什么人们更喜欢自顶向下的分析方法。只要能写出文法规则，那么翻译成代码的过程就非常直接。

这里我只给出了部分代码，完整的代码，你可以在这里找到。

但是你也要注意这种算法的一个重要限制，那就是不能有左递归。例如，表达式文法还有一种写法是这样的：

$expr \rightarrow expr + term$

这种文法规则右侧的第一个非终结符和左侧的非终结符相同，这种情况就是左递归。如果采用自底向上的归约的办法，显然是可以把右侧的三个符号归约成左侧的一个符号的。但是对于自顶向下的算法就不行了。对它直接进行翻译，会产生如下代码：

int expr() {
    int a = expr(); /* 请注意这里，这是个没有终结条件的递归 */

    if (t->_type == TT_ADD) {
        t = next_token();
        int b = term();
        a += b;
    }
    return a;
}

很明显，这是一个无穷递归。这也就说明了自顶向下的分析方法处理不了左递归。
遇到这种情况，我们可以通过将左递归文法改写成右递归文法，来避免无穷递归的问题。例如，上面提到的expr可以这样改写：

$expr \rightarrow term~epxr’$

$expr’ \rightarrow +term~expr’~|~\epsilon$

其中，$\epsilon$代表空，这表示expr’可以推导为空。这就把左递归文法改成了右递归，从而避免了翻译成代码时的无穷递归。把这个文法翻译成代码的练习就交给你自己完成了，欢迎在评论区交流你的心得。

我在做文法分析的过程中直接把表达式的值求出来了，但实际上，编译器并不会在文法分析阶段就对程序进行运算，而是会把程序先翻译成一种叫作抽象语法树（Abstract Syntax Tree, AST）的树形结构，然后再对这个树形结构做分析和变换，进而翻译成机器指令。接下来，我们就看一下抽象语法树的相关知识。

抽象语法树

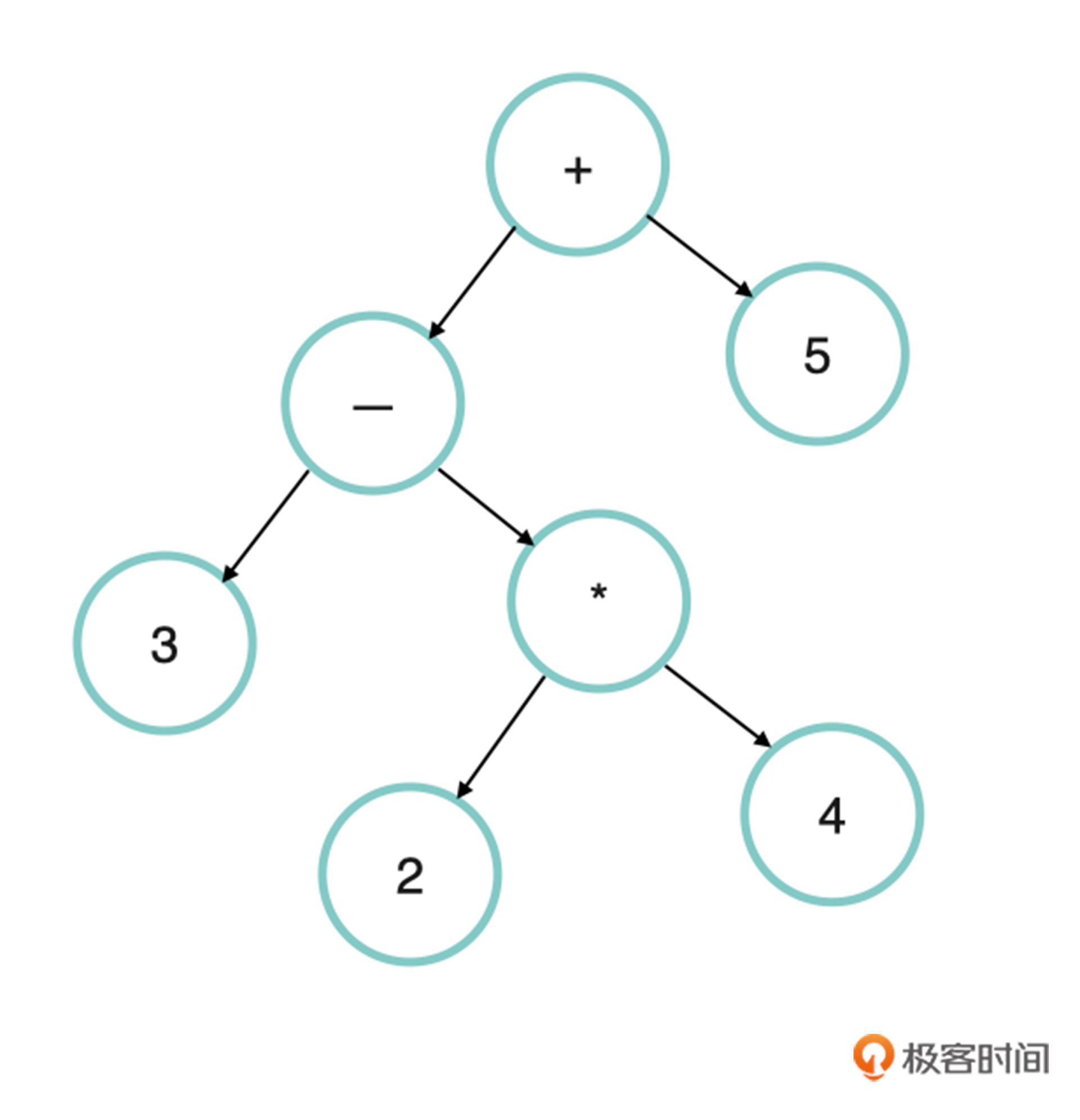
我先用一个直观的例子来向你展示什么是抽象语法树。对于表达式“3 - 2 * 4 + 5”，它的抽象语法树如下图所示：

递归的函数调用本质上也是一棵树（如果你对这句话感到费解，可能需要先学习下数据结构相关的知识。不过这里看不懂也没关系，不影响对这节课主要内容的理解）。如果我们把递归函数的轨迹都使用一种结构记录下来，就可以得到这棵树。接下来，我直接通过代码来展示如何做这种记录，以及如何产生抽象语法树。

第一步，先定义抽象语法树的结点。

从上图中可知，一个表达式中包含了加减乘除运算的结点和代表整数的结点。所以，我们可以这样定义AST结点：

// ast.h
enum NodeType {
    NT_INT,

    NT_ADD,
    NT_SUB,
    NT_MUL,
    NT_DIV
};

typedef struct {
    enum NodeType ntype;
} Node;

typedef struct {
    Node parent;
    int value;
} IntNode;

typedef struct {
    Node parent;
    Node* left;
    Node* right;
} BinOpNode;

第二步，定义创建这些结点的函数：

Node* create_int(int v) {
    IntNode* in = (IntNode*)malloc(sizeof(IntNode));
    in->value = v;
    in->parent.ntype = NT_INT;
    return (Node*) in;
}

Node* create_binop(enum TokenType tt, Node* left, Node* right) {
    BinOpNode* node = (BinOpNode*) malloc(sizeof(BinOpNode));
    node->left = left;
    node->right = right;
    if (tt == TT_ADD) {
        node->parent.ntype = NT_ADD;
    }
    else if (tt == TT_SUB) {
        node->parent.ntype = NT_SUB;
    }
    else if (tt == TT_DIV) {
        node->parent.ntype = NT_DIV;
    }
    else if (tt == TT_MUL) {
        node->parent.ntype = NT_MUL;
    }

    return (Node*) node;
}

第三步，我们再把文法分析的过程从直接计算值改成创建抽象语法树结点：

/* 表达式对应的函数 */
Node* expr() {
    Node* a = NULL, *b = NULL;
    a = term();

    while (t->_type == TT_ADD || t->_type == TT_SUB) {
        if (t->_type == TT_ADD) {
            t = next_token();
            b = term();
            /* 这里不再是直接计算，而是生成一个语法树结点 */
            a = create_binop(TT_ADD, a, b);
        }
        else if (t->_type == TT_SUB) {
            t = next_token();
            b = term();
            a = create_binop(TT_SUB, a, b);
        }
    }

    return a;
}

/* 项的规则 */
Node* term() {
    Node* a = NULL, *b = NULL;
    a = factor();

    while (t->_type == TT_MUL || t->_type == TT_DIV) {
        if (t->_type == TT_MUL) {
            t = next_token();
            b = factor();
            a = create_binop(TT_MUL, a, b);
        }
        else if (t->_type == TT_DIV) {
            t = next_token();
            b = factor();
            a = create_binop(TT_DIV, a, b);
        }
    }

    return a;
}

/* 因子的规则 */
Node* factor() {
    if (t->_type == TT_INTEGER) {
        /* 创建一个代表整型的语法树结点 */
        Node* a = create_int(t->_value._int);
        t = next_token();
        return a;
    }
    else if (t->_type == TT_LEFT_PAR) {
        t = next_token();
        Node* a = expr();
        if (!match(TT_RIGHT_PAR))
            return NULL;
        else
            return a;
    }
    else {
        printf("Parse Error\n");
        return NULL;
    }
}

这个过程是比较简单的，我就不再解释了，你可以参考我加的注释来理解。最后，我们可以再使用二叉树的遍历来验证我们创建的抽象语法树是不是正确的：

void post_order(Node* root) {
    if (root->ntype == NT_INT) {
        printf("%d ", ((IntNode*)root)->value);
    }
    else {
        BinOpNode* binop = (BinOpNode*)root;
        post_order(binop->left);
        post_order(binop->right);

        enum NodeType tt = root->ntype;
        if (tt == NT_ADD) {
            printf("+ ");
        }
        else if (tt == NT_SUB) {
            printf("- ");
        }
        else if (tt == NT_DIV) {
            printf("/ ");
        }
        else if (tt == NT_MUL) {
            printf("* ");
        }
    }
}

运行这个程序，就会发现我们已经成功地把中缀表达式转成了后缀表达式输出。后缀表达式也叫作逆波兰序表达式。如果上述代码不使用后序遍历，而是使用前序遍历，程序的输出就是前缀表达式，你可以自己尝试一下。

更进一步，如果我们在对这个抽象语法树进行遍历的时候，同时进行求值和计算，这个过程就叫作解释执行。不同于编译执行，解释执行往往没有经过比较好的优化，所以它的执行效率往往比较低。

到这里，关于文法分析的知识我就介绍完了。

总结

这节课，我讲解了编译过程中的一个重要步骤，那就是文法分析。文法是一套语言产生的规则，根据文法规则来判断源文件是否符合文法的过程就是文法分析。

文法分析的方法主要分为两种，分别是自顶向下和自底向上的分析方法。其中，自底向上主要采用归约的办法，将终结符归约成顶级的非终结符，多数自动化工具都是采用了这种方法。而自顶向下的分析方法则比较简单明了，更符合人的直观思维。

自顶向下的分析方法简单地将非终结符转换成函数，把或结构转换成if语句，把多项结构转换成while语句。所以这种分析方法是不能处理左递归的，但是所有的左递归文法都可以按一定的模式转换成右递归的。

在编译器里，文法分析并不是直接对源文件进行求值运算的，而是会生成抽象语法树。它本质上是一棵树，我们可以通过遍历这棵树，对它进行各种变换，比如转换成字节码，或者其他的中间表示，等等。这些内容我将会在下节课进行讲解。

课后练习

你可以尝试定义C语言的变量定义、分支语句和循环语句的文法，并将它实现出来。这些完成以后，你基本上就可以得到一个可执行简单语句的小型C语言解释器了。完整的代码我放在了gitee上，供你参考。这里是if语句的实现，这里是变量定义和赋值的实现。

这节课就到这里了，如果今天的内容让你有所收获，欢迎把它分享给你的朋友。下一次的加餐，我将继续按顺序讲解 C 语言程序编译的基本步骤，我们到时候见！