你好，我是王喆。

今天，我想用一节课的时间，带你梳理巩固一下深度学习的相关基础知识。打好基础之后，我们再去学习深度学习推荐系统的技术细节，就能更加得心应手了。

具体来说，我会从一个基本的神经元开始，讲到多神经元组成的神经网络，再到结构各异的深度学习网络，最后再讲一讲深度学习和推荐系统是怎么结合的。这样，从0到1带你体会深度学习网络生长的整个过程。

是不是已经迫不及待想要开始今天的课程啦？接下来，我们就一起“钻”进一个神经元里面，跟它一起成长吧。

一切要从一个神经元开始

上中学的时候，你肯定在生物课上学到过，神经元是我们神经系统的最基本单元，我们的大脑、小脑、脊髓都是由神经元组成的。比如，大脑大概包含了1000亿个神经元！正是这些小小的神经元之间互相连接合作，让大脑能够完成非常复杂的学习任务，这是一个多么神奇的过程！

于是，计算机科学家们就有一个设想，是不是我们也能从神经元出发，创造出一个人造大脑，来帮我们完成各种不同的任务呢？这其中当然也包括我们课程要讲的推荐任务。事实上，随着近十年深度学习网络的快速发展，这个设想已经被成功应用到图像识别、语音处理、推荐搜索等多个领域了！那组成这个“人造大脑”的基础，也就是神经元到底是什么样子的呢？

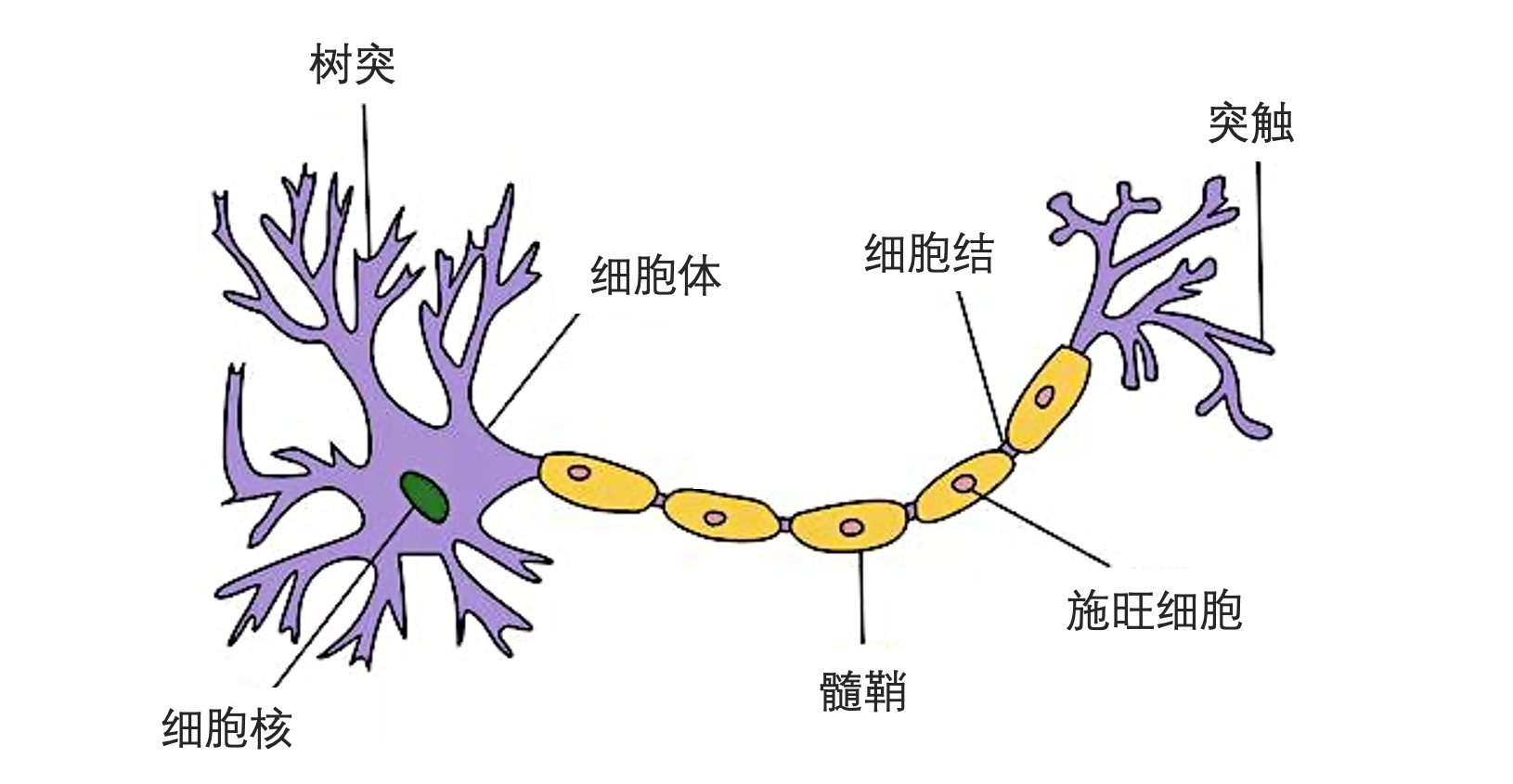
下面这张图就是一个神经元的结构示意图，它大致由树突、细胞体（图中细胞核和周围的部分）、轴突、轴突末梢等几部分组成。树突是神经元的输入信号通道，它的功能是将其他神经元的动作电位（可以当作一种信号）传递至细胞体。

在接收到其他神经元的信号后，细胞体会根据这些信号改变自己的状态，变成“激活态”还是“未激活态”。具体的状态取决于输入信号，也取决于神经细胞本身的性质（抑制或加强）。当信号量超过某个阈值时，细胞体就会被激活，产生电脉冲。电脉冲会沿着轴突传播，并通过轴突末梢传递到其它神经元。

我上面讲的这些是神经元工作的生物学过程，那如果要用一个神经元来解决推荐问题，具体又该怎么做呢？举个例子，我们可以假设其他神经元通过树突传递过来的信号就是推荐系统用到的特征，有的信号可能是“用户性别是男是女”，有的信号可能是“用户之前有没有点击过这个物品”等等。细胞体在接收到这些信号的时候，会做一个简单的判断，然后通过轴突输出一个信号，这个输出信号大小代表了用户对这个物品的感兴趣程度。这样一来，我们就可以用这个输出信号给用户做推荐啦。

看起来用神经元来完成推荐任务还是很有希望的，但在实际应用里面，我们还得把生物结构的神经元抽象成一个数学形式，这样我们才能用程序来实现它。图2就是这样的一个抽象结构，这个神经元的结构很简单，只有两个传递输入信号的树突。

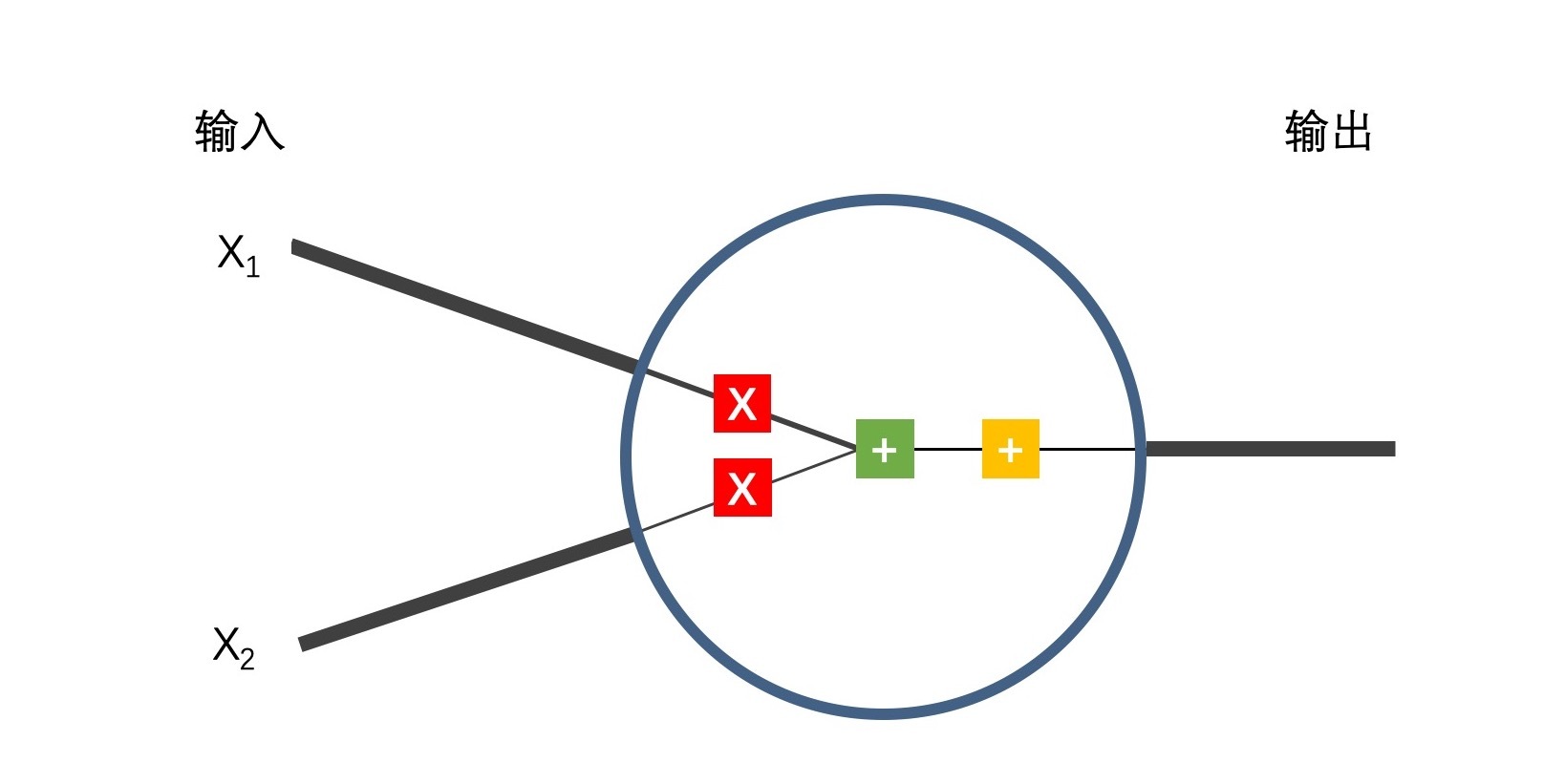
我们可以看到，图2中的x₁、x₂就相当于两个树突传递的输入信号，蓝圈内的结构相当于神经元的细胞体，细胞体用某种方式处理好输入信号之后，就通过右面的轴突输出信号y。因为输入输出都很简单，所以我想现在你的疑问，肯定聚焦在细胞体对输入信号的处理方式上了，我们可以把细胞体的数学结构放大一点看看。

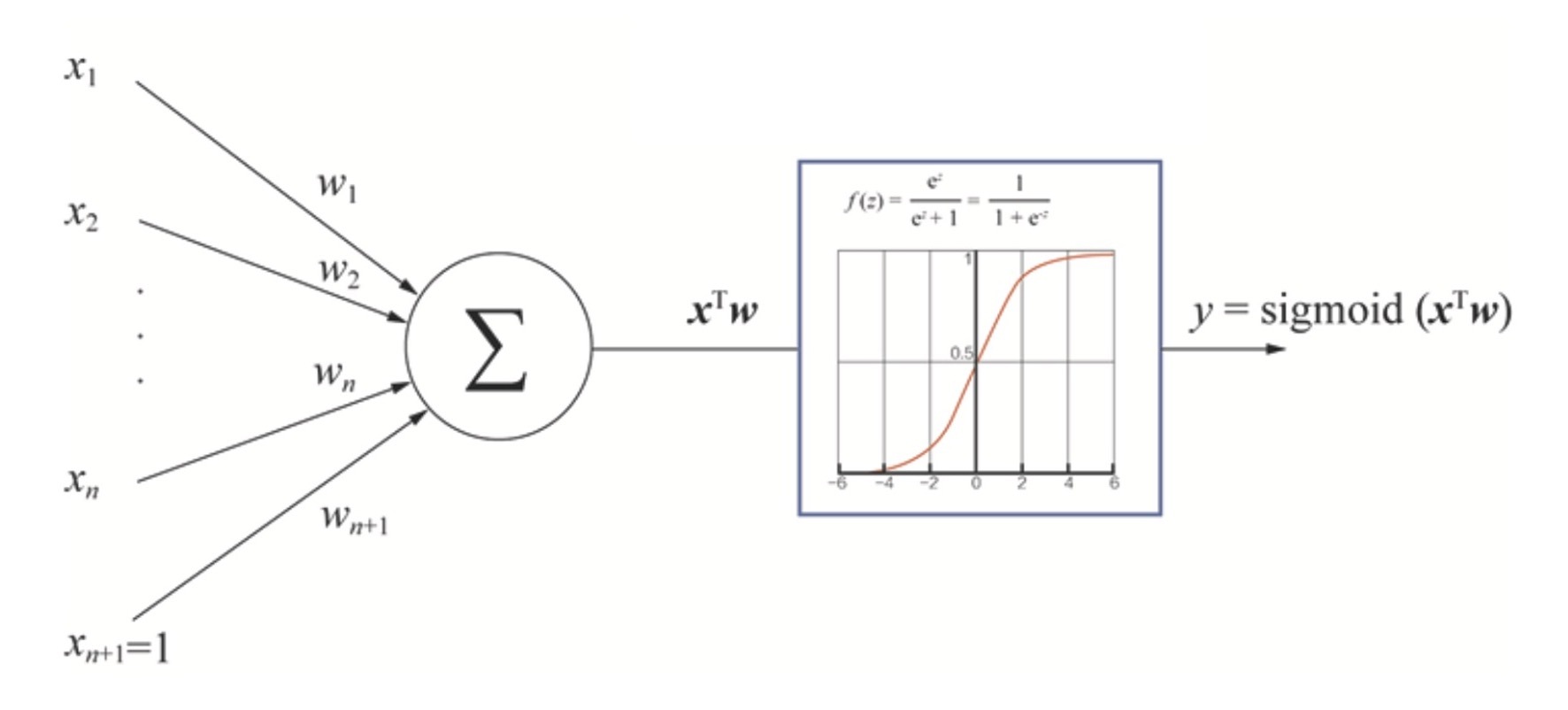
其实细胞体中的计算就做了两件事情，一件事情是把输入信号x₁、x₂各自乘以一个权重w₁、w₂，再把各自的乘积加起来之后输入到一个叫“激活函数”的结构里。

图3中的激活函数是sigmoid激活函数，它的数学定义是：$f(z)=\frac{1}{1+\mathrm{e}^{-z}}$ 。它的函数图像就是图3中的S型曲线，它的作用是把输入信号从（-∞，+∞）的定义域映射到（0，1）的值域（因为在点击率预测，推荐问题中，往往是要预测一个从0到1的概率）。再加上sigmoid函数有处处可导的优良数学形式，方便之后的梯度下降学习过程，所以它成为了经常使用的激活函数。

当然，激活函数的种类有很多种，比较流行的还有tanh、ReLU等，在训练神经元或者神经网络的时候，我们可以尝试多种激活函数，根据效果来做最终的决定。

什么是神经网络？

不过，单神经元由于受到简单结构的限制，预测能力并不强，因此在解决复杂问题时，我们经常会用多神经元组成一个网络，这样它就具有更强的拟合数据的能力了，这也就是我们常说的神经网络。比如说，下图就向我们展示了一个由输入层、两神经元隐层和单神经元输出层组成的简单神经网络。

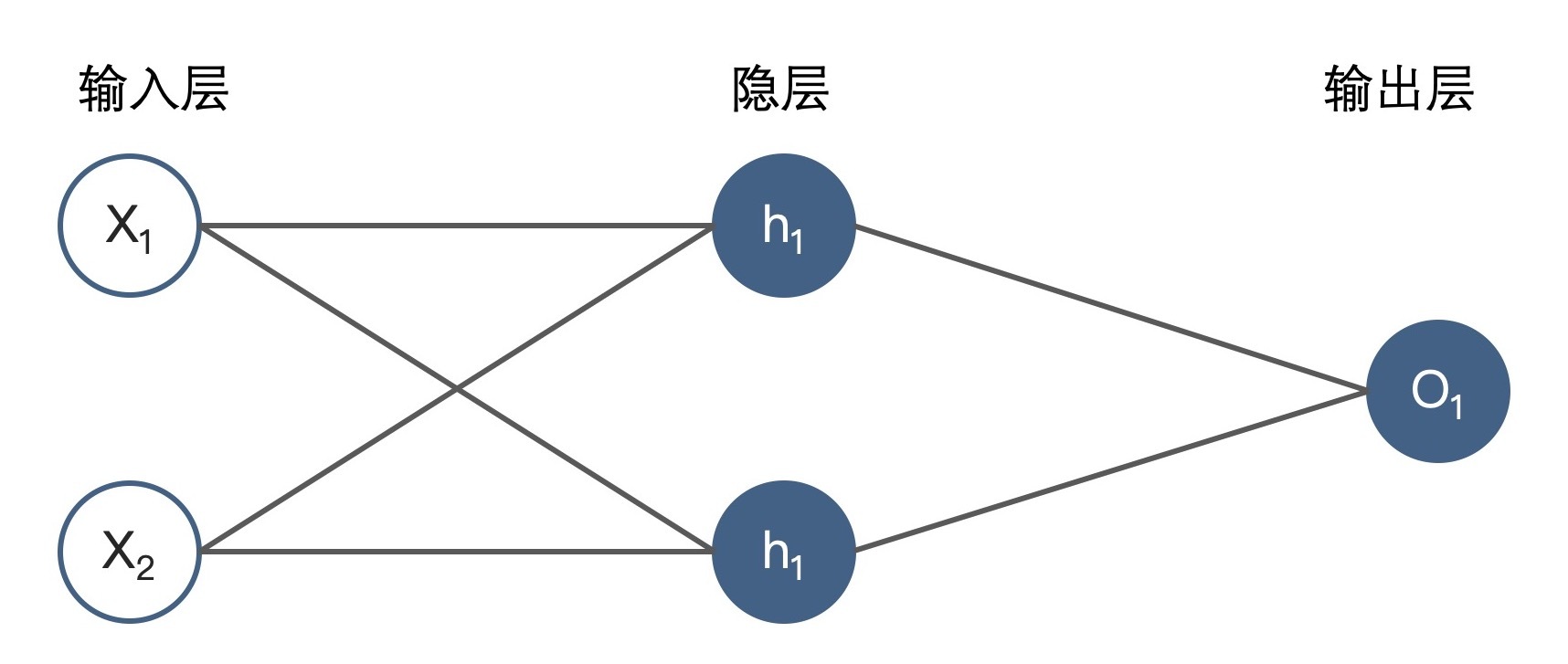
其中，每个蓝色神经元的构造都和刚才的单神经元构造相同，h₁和h₂神经元的输入是由x₁和x₂组成的特征向量，而神经元o₁的输入则是由h₁和h₂输出组成的输入向量。这是一个最简单的三层神经网络，在深度学习的发展过程中，正是因为研究人员对神经元不同的连接方式的探索，才衍生出各种不同特性的深度学习网络，让深度学习模型的家族树枝繁叶茂。在后面课程的学习中，我们也会深入讲解各种不同的网络结构，相信你对这句话的理解也会随着学习的推进而更加深刻。

神经网络是怎么学习的？

清楚了神经网络的结构之后，更重要的问题是我们该如何训练一个神经网络。也就是说，我们怎么得到图5中x₁到h₁、h₂的权重w₁、w₃，以及图中其他的权重呢？

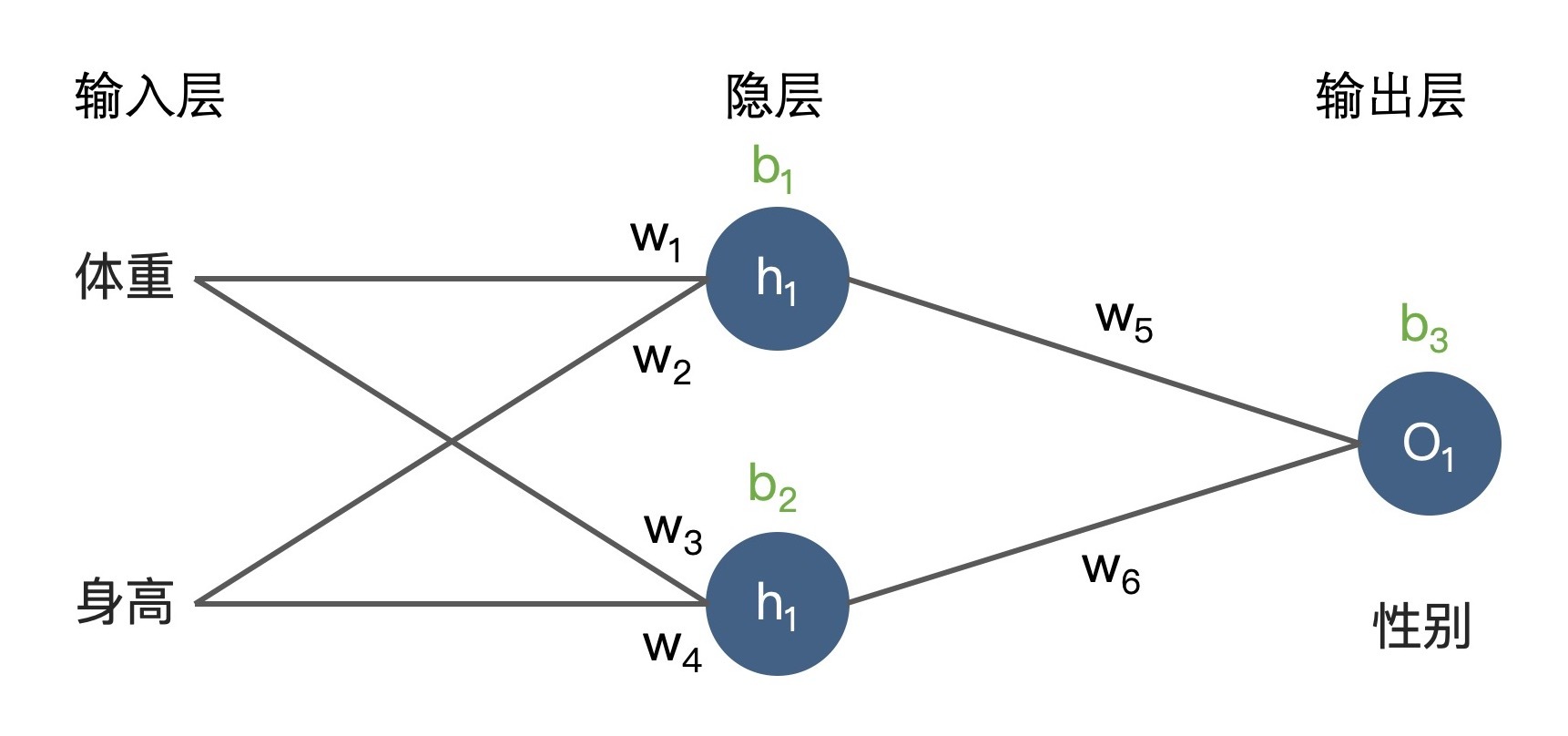
这里需要用到神经网络的重要训练方法，前向传播（Forward Propagation）和反向传播（Back Propagation）。前向传播的目的是在当前网络参数的基础上得到模型对输入的预估值，也就是我们常说的模型推断过程。比如说，我们要通过一位同学的体重、身高预测TA的性别，前向传播的过程就是给定体重值71，身高值178，经过神经元h₁、h₂和o₁的计算，得到一个性别概率值，比如说0.87，这就是TA可能为男性的概率。

在得到预估值之后，我们就可以利用损失函数（Loss Function）计算模型的损失。比如我们采用绝对值误差（Absolute Loss）作为我们的损失函数，如果这位同学的真实性别是男，那真实的概率值就是1，根据公式2的绝对值误差定义，这次预测的损失就是|1-0.87| = 0.13。

$$l_{1}\left(y_{i}, \hat{y}_{i}\right)=\left|y_{i}-\hat{y}_{i}\right|$$

我们常说“知错能改，善莫大焉”，神经网络的学习更是践行了这句话。发现了预测值和真实值之间的误差（Loss），我们就要用这个误差来指导权重的更新，让整个神经网络在下次预测时变得更准确。最常见的权重更新方式就是梯度下降法，它是通过求取偏导的形式来更新权重的。比如，我们要更新权重w₅，就要先求取损失函数到w5的偏导$\frac{\partial L_{o 1}}{\partial w_{5}}$。从数学角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数下降最快的方向，所以让损失函数减小最快的方向就是我们希望梯度w5更新的方向。这里我们再引入一个超参数α，它代表了梯度更新的力度，也称为学习率。好，现在我们可以写出梯度更新的公式了：$w_{5}^{t+1}=w_{5}^{t}-\alpha * \frac{\partial L_{o 1}}{\partial w_{5}}$。公式中的w₅当然可以换成其他要更新的参数，公式中的t代表着更新的次数。

对输出层神经元来说（图中的 o₁），我们可以直接利用梯度下降法计算神经元相关权重（即图5中的权重w₅和w₆）的梯度，从而进行权重更新，但对隐层神经元的相关参数（比如w₁），我们又该如何利用输出层的损失进行梯度下降呢？

答案是“利用求导过程中的链式法则（Chain Rule）”。通过链式法则我们可以解决梯度逐层反向传播的问题。最终的损失函数到权重w₁的梯度是由损失函数到神经元h₁输出的偏导，以及神经元h₁输出到权重w₁的偏导相乘而来的。也就是说，最终的梯度逐层传导回来，“指导”权重w₁的更新。

$$\frac{\partial L_{o 1}}{\partial w_{1}}=\frac{\partial L_{o 1}}{\partial h_{1}} \cdot \frac{\partial h_{1}}{\partial w_{1}}$$

具体在计算的时候，我们需要根据具体的问题明确最终损失函数的形式，以及每层神经元激活函数的形式，再根据具体的函数形式进行偏导的计算。这部分的学习需要一定的微积分基础，如果你觉得不是很好理解，也不用担心，因为对于大部分的机器学习库来说，梯度反向传播的过程已经被实现并且封装好了，直接调用就可以了，但是原理我们还是有必要了解的。

到这里，神经网络相关的基本知识我们就讲完了，前面讲了这么多，我想再带你做个总结。神经元是神经网络中的基础结构，它参照生物学中的神经元构造，抽象出带有输入输出和激活函数的数学结构。而神经网络是通过将多个神经元以串行、并行、全连接等方式连接起来形成的网络，神经网络的训练方法是基于链式法则的梯度反向传播。

但是细心的你可能会问了，搭建深度学习推荐系统跟神经网络到底有什么关系呢？

神经网络与深度学习的关系是什么？

想要搞清楚这个问题，我得先给你讲点儿神经网络和深度学习的历史。

其实学术界对于人工神经网络的研究非常早，可以追溯上世纪60年代，但由于计算机发展本身的限制，我们没有办法完成神经网络学习所需的大量计算。直到上世纪80年代，Hinton等人提出了反向传播算法（BP算法），神经网络才能够完成类似字母识别的简单任务。

时间到了2012年，Hinton的学生Alex Krizhevsky提出了一个用于图像识别的深度神经网络结构AlexNet，在当年著名的图像识别大赛ImageNet上，它以碾压第二名的成绩荣获桂冠。也正是从那时起，人们突然意识到，原来用深层的神经网络可以完成这么复杂的任务。深度学习的浪潮从此被正式引爆了！

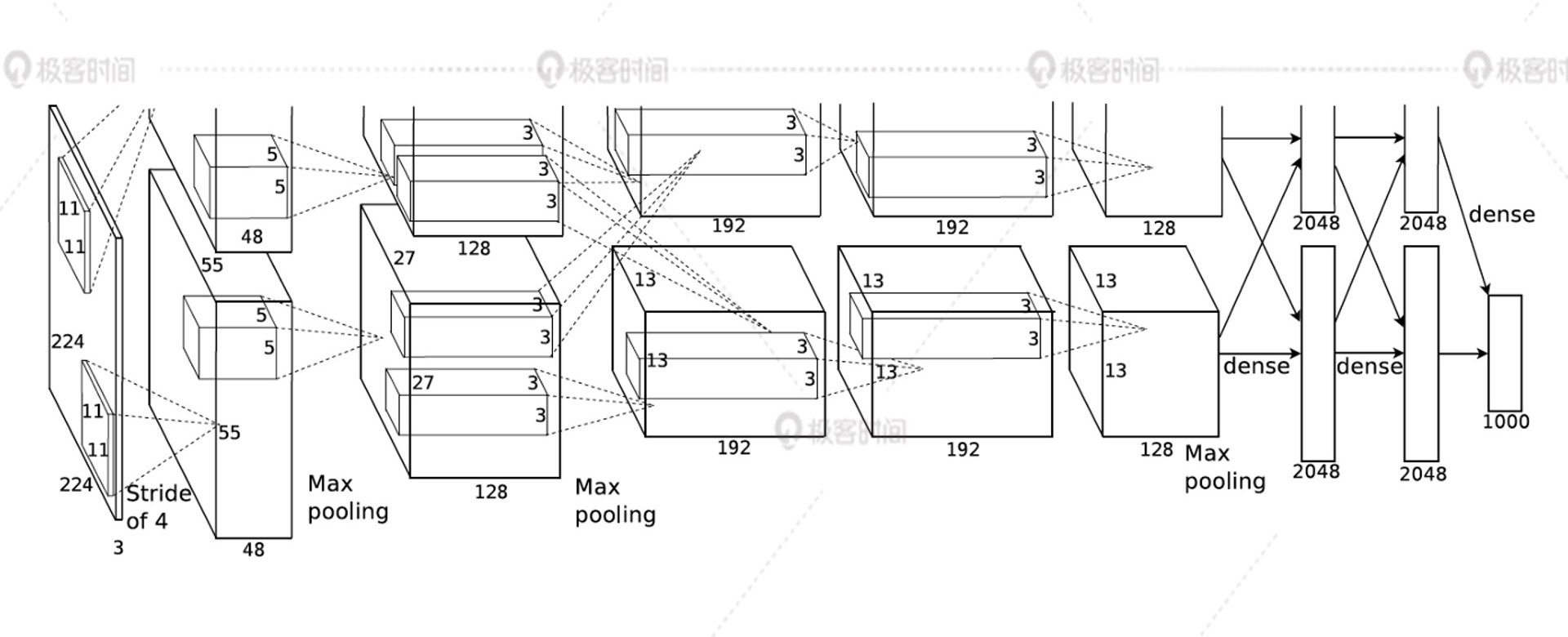
结合上图你可以看到，跟我们刚才讲的简单神经网络相比，AlexNet无论从深度，还是每一层的神经元数量来说，都大大增加了，并且神经元的连接方式和种类也更加丰富。

那知道了这些，我们就可以回答刚才提出的问题了。深度学习可以说是神经网络的延伸和发展，它极大地丰富神经网络的结构种类，让它能够处理各类复杂问题。

这个时候，你可能又会问：好像深度学习相比传统的神经网络没什么革命性的创新呀，为啥到了2012年才取得这么大的突破呢？这是个好问题，我觉得主要有三个原因。

一是算力的极大提高。 到了2012年，随着GPU大量应用于机器学习领域，神经网络的训练速度也有了量级上的提高，时至今日，OpenAI刚发布的语言模型GPT-3居然有高达1750亿个参数，这放在十年前是完全不可想像的。

二是数据的极大丰富。 之前神经网络面临的一大问题是，在训练数据量较小的情况下，模型难以收敛。但随着越来越多成熟的大数据开源平台，以及越来越多丰富的开源数据集的出现，即使神经网络的结构变得越来越复杂，我们也完全可以凭借海量的训练数据使它完全收敛。

三是深度学习理论的进一步发展。 虽然深度学习是站在“神经网络”这一巨人的肩膀上发展起来的，但专家们也取得了非常多的理论创新，就比如，pooling层的加入和成功应用，各类更适合深度学习的梯度下降方法的提出等等，这些都让深度学习的应用成为了可能。

深度学习是如何应用在推荐系统中的？

前面我们介绍的都是通用的深度学习知识，但深度学习又是如何应用在推荐系统中的呢？下面，我就着重来说说这一点。

在刚才讲解神经元原理的时候，我讲到用单个神经元可以预测用户对物品感兴趣的程度。事实上，无论是单个神经元，还是结构非常复杂的深度学习网络，它们在推荐系统场景下要解决的问题都是一样的，就是预测用户对某个物品的感兴趣程度，这个感兴趣程度往往是一个概率，最典型的就是点击率、播放率、购买概率等。

所以在深度学习时代，我们使用深度学习模型替代了传统的推荐模型，目的就是让它作出更准确的推荐。但像上节课提出的，深度学习的革命要求我们对算力、数据都作出大幅度的调整，而这些调整因为涉及到分布式计算平台、深度学习平台，以及线上的模型服务部分，所以我们需要在推荐系统的整体架构上都作出不小的改造，让它适应深度学习时代的需求。这也是我们学习这门课的目的所在。

小结

今天，我带你学习了深度学习的基础知识。我们从神经元学到了神经网络，再到训练神经网络的方法，以及神经网络和深度学习的关系。今天的知识点比较密集，而且每个知识点之间都是层层递进的。为了方便你记忆，我把本节课的重点整理成了一张表格，帮你巩固所学。

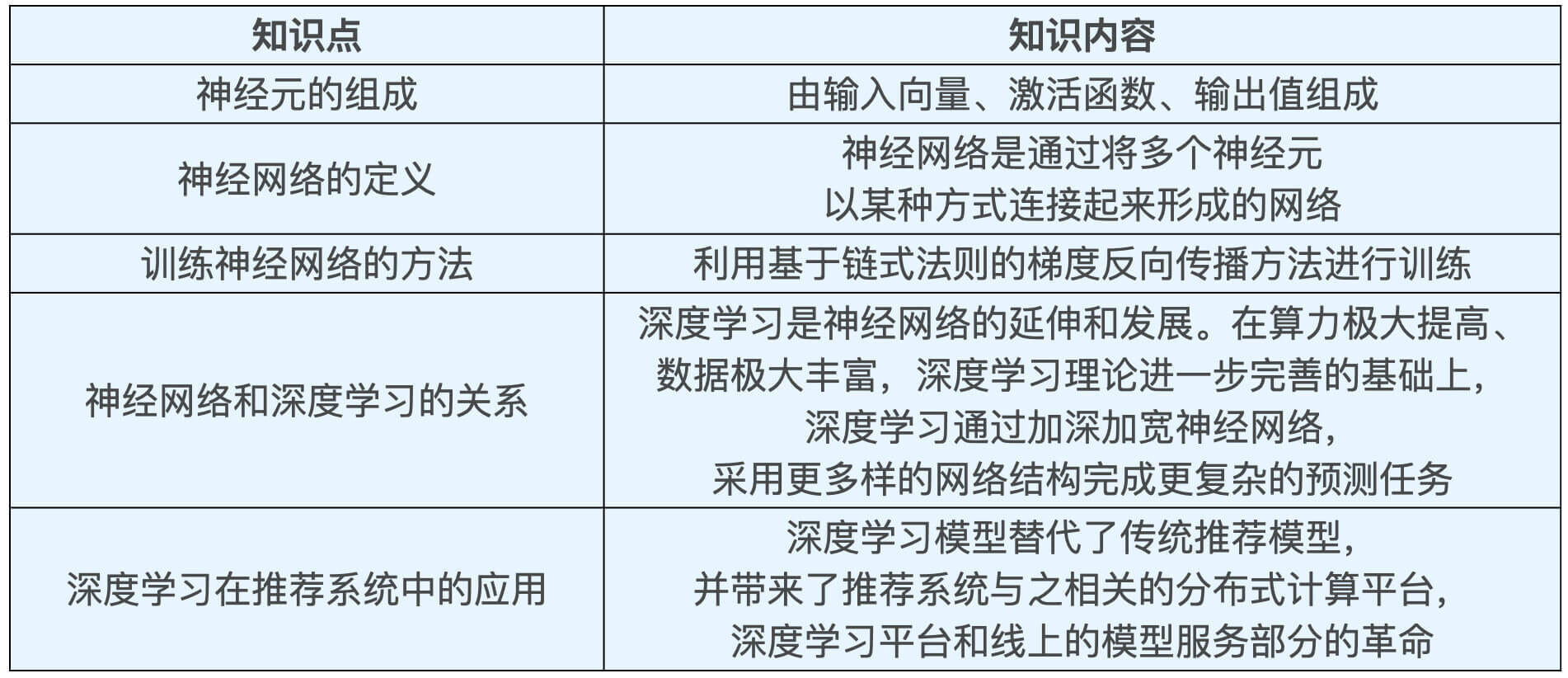
这些知识是未来我们搭建深度学习推荐系统的基础。我希望你能够在动手实践之前完全掌握它。从下节课开始，我们就会进入深度学习推荐系统技术细节和实战环节，你准备好了吗？

课后思考

你觉得都有哪些因素影响着深度学习网络的结构？深度学习模型是越深越好吗？为什么？

欢迎在留言区分享你的答案和疑惑，如果你的朋友也想了解神经网络和深度学习的基本知识，也欢迎你把这节课分享给他。好了，今天的内容就到这里了，我们下节课见！