你好，我是王喆。

上一节课，我们一起学习了Embedding技术。我们知道，只要是能够被序列数据表示的物品，都可以通过Item2vec方法训练出Embedding。但是，互联网的数据可不仅仅是序列数据那么简单，越来越多的数据被我们以图的形式展现出来。这个时候，基于序列数据的Embedding方法就显得“不够用”了。但在推荐系统中放弃图结构数据是非常可惜的，因为图数据中包含了大量非常有价值的结构信息。

那我们怎么样才能够基于图结构数据生成Embedding呢？这节课，我们就重点来讲讲基于图结构的Embedding方法，它也被称为Graph Embedding。

互联网中有哪些图结构数据？

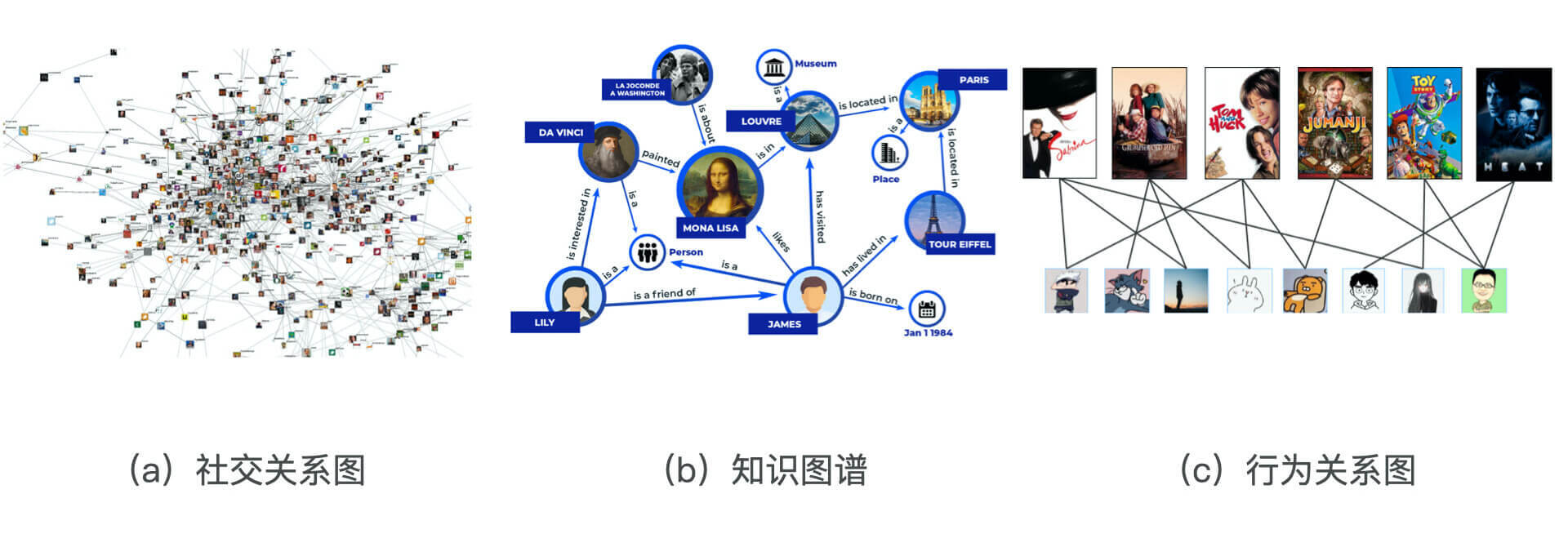
可能有的同学还不太清楚图结构中到底包含了哪些重要信息，为什么我们希望好好利用它们，并以它们为基础生成Embedding？下面，我就先带你认识一下互联网中那些非常典型的图结构数据（如图1）。

事实上，图结构数据在互联网中几乎无处不在，最典型的就是我们每天都在使用的社交网络（如图1-a）。从社交网络中，我们可以发现意见领袖，可以发现社区，再根据这些“社交”特性进行社交化的推荐，如果我们可以对社交网络中的节点进行Embedding编码，社交化推荐的过程将会非常方便。

知识图谱也是近来非常火热的研究和应用方向。像图1b中描述的那样，知识图谱中包含了不同类型的知识主体（如人物、地点等），附着在知识主体上的属性（如人物描述，物品特点），以及主体和主体之间、主体和属性之间的关系。如果我们能够对知识图谱中的主体进行Embedding化，就可以发现主体之间的潜在关系，这对于基于内容和知识的推荐系统是非常有帮助的。

还有一类非常重要的图数据就是行为关系类图数据。这类数据几乎存在于所有互联网应用中，它事实上是由用户和物品组成的“二部图”（也称二分图，如图1c）。用户和物品之间的相互行为生成了行为关系图。借助这样的关系图，我们自然能够利用Embedding技术发掘出物品和物品之间、用户和用户之间，以及用户和物品之间的关系，从而应用于推荐系统的进一步推荐。

毫无疑问，图数据是具备巨大价值的，如果能将图中的节点Embedding化，对于推荐系统来说将是非常有价值的特征。那下面，我们就进入正题，一起来学习基于图数据的Graph Embedding方法。

基于随机游走的Graph Embedding方法：Deep Walk

我们先来学习一种在业界影响力比较大，应用也很广泛的Graph Embedding方法，Deep Walk，它是2014年由美国石溪大学的研究者提出的。它的主要思想是在由物品组成的图结构上进行随机游走，产生大量物品序列，然后将这些物品序列作为训练样本输入Word2vec进行训练，最终得到物品的Embedding。因此，DeepWalk可以被看作连接序列Embedding和Graph Embedding的一种过渡方法。下图2展示了DeepWalk方法的执行过程。

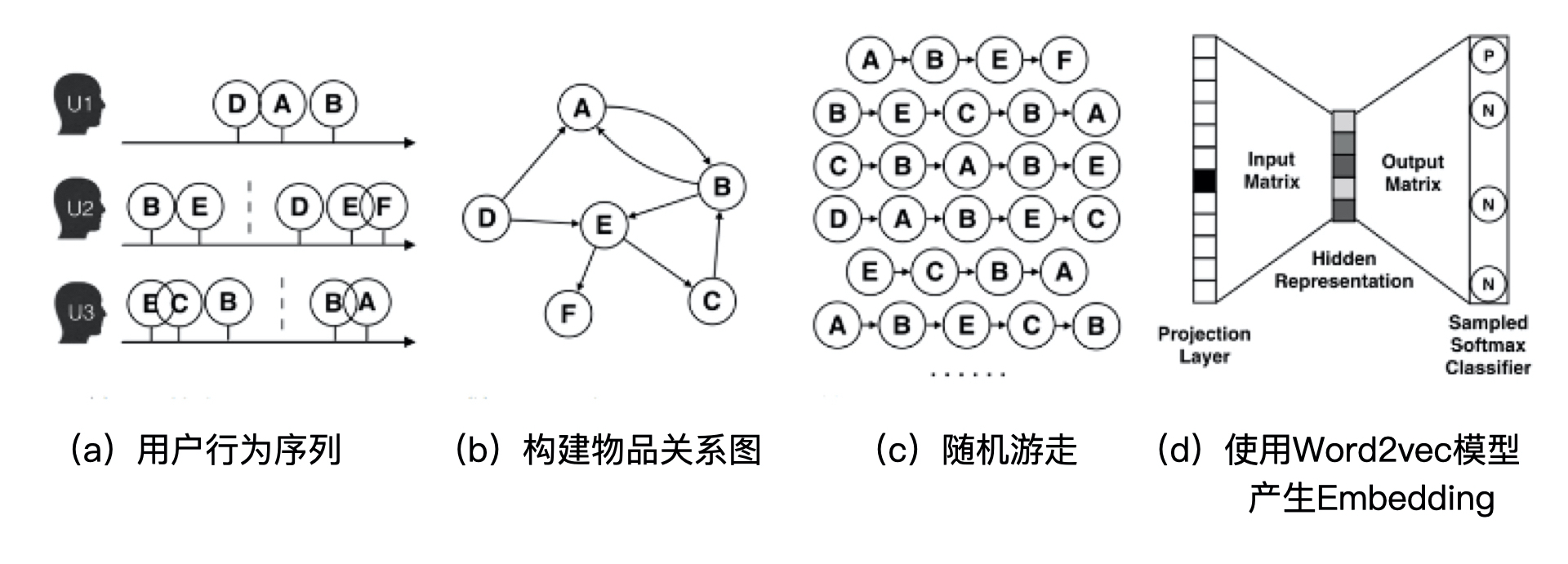
接下来，我就参照图2中4个示意图，来为你详细讲解一下DeepWalk的算法流程。

首先，我们基于原始的用户行为序列（图2a），比如用户的购买物品序列、观看视频序列等等，来构建物品关系图（图2b）。从中，我们可以看出，因为用户U_i先后购买了物品A和物品B，所以产生了一条由A到B的有向边。如果后续产生了多条相同的有向边，则有向边的权重被加强。在将所有用户行为序列都转换成物品相关图中的边之后，全局的物品相关图就建立起来了。

然后，我们采用随机游走的方式随机选择起始点，重新产生物品序列（图2c）。其中，随机游走采样的次数、长度等都属于超参数，需要我们根据具体应用进行调整。

最后，我们将这些随机游走生成的物品序列输入图2d的Word2vec模型，生成最终的物品Embedding向量。

在上述DeepWalk的算法流程中，唯一需要形式化定义的就是随机游走的跳转概率，也就是到达节点v_i后，下一步遍历v_i 的邻接点v_j 的概率。如果物品关系图是有向有权图，那么从节点v_i 跳转到节点v_j 的概率定义如下：

$$P\left(v_{j} \mid v_{i}\right)=\left\{\begin{array}{ll}\frac{M_{i j}}{\sum_{j \in N_{+}\left(V_{i}\right)}}, m_{i j} & v_{j} \in N_{+}\left(v_{i}\right) \\\ 0, & \mathrm{e}_{i j} \notin \varepsilon\end{array}\right.$$

其中，N+(v_i)是节点v_i所有的出边集合，M_ij是节点v_i到节点v_j边的权重，即DeepWalk的跳转概率就是跳转边的权重占所有相关出边权重之和的比例。如果物品相关图是无向无权重图，那么跳转概率将是上面这个公式的一个特例，即权重M_ij将为常数1，且N+(v_i)应是节点v_i所有“边”的集合，而不是所有“出边”的集合。

再通过随机游走得到新的物品序列，我们就可以通过经典的Word2vec的方式生成物品Embedding了。当然，关于Word2vec的细节你可以回顾上一节课的内容，这里就不再赘述了。

在同质性和结构性间权衡的方法，Node2vec

2016年，斯坦福大学的研究人员在DeepWalk的基础上更进一步，他们提出了Node2vec模型。Node2vec通过调整随机游走跳转概率的方法，让Graph Embedding的结果在网络的同质性（Homophily）和结构性（Structural Equivalence）中进行权衡，可以进一步把不同的Embedding输入推荐模型，让推荐系统学习到不同的网络结构特点。

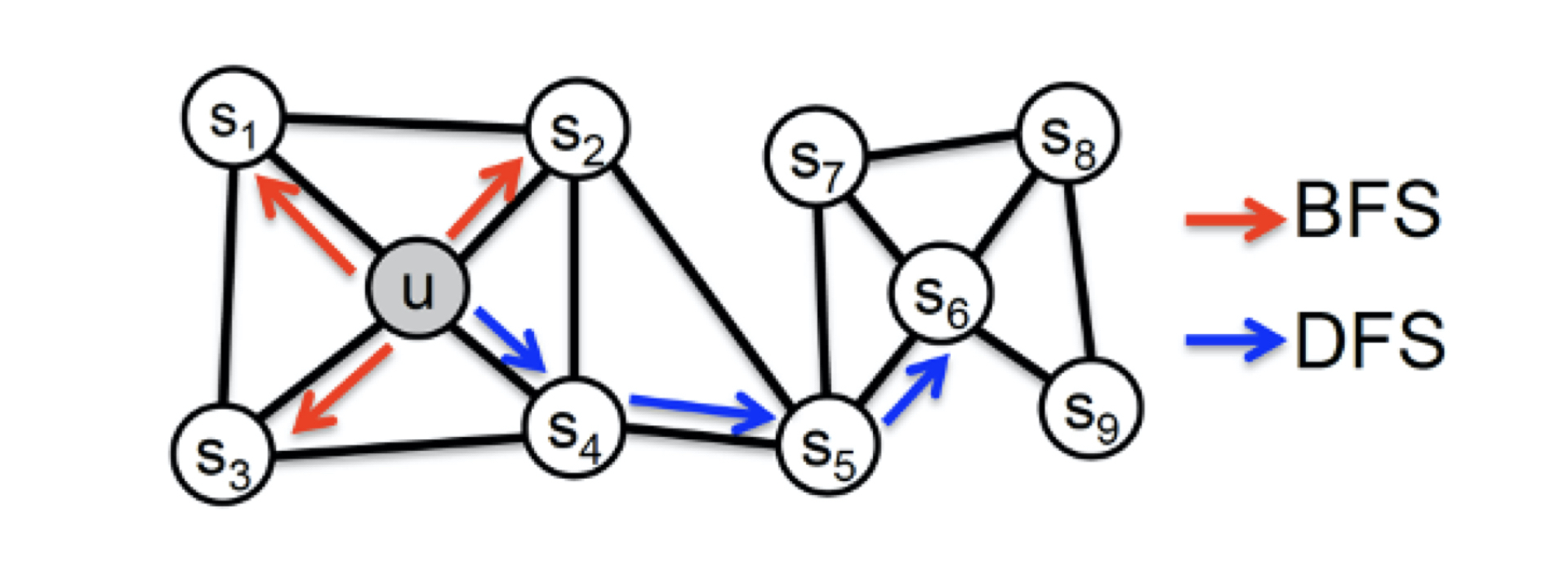
我这里所说的网络的“同质性”指的是距离相近节点的Embedding应该尽量近似，如图3所示，节点u与其相连的节点s₁、s₂、s₃、s₄的Embedding表达应该是接近的，这就是网络“同质性”的体现。在电商网站中，同质性的物品很可能是同品类、同属性，或者经常被一同购买的物品。

而“结构性”指的是结构上相似的节点的Embedding应该尽量接近，比如图3中节点u和节点s₆都是各自局域网络的中心节点，它们在结构上相似，所以它们的Embedding表达也应该近似，这就是“结构性”的体现。在电商网站中，结构性相似的物品一般是各品类的爆款、最佳凑单商品等拥有类似趋势或者结构性属性的物品。

理解了这些基本概念之后，那么问题来了，Graph Embedding的结果究竟是怎么表达结构性和同质性的呢？

首先，为了使Graph Embedding的结果能够表达网络的“结构性”，在随机游走的过程中，我们需要让游走的过程更倾向于BFS（Breadth First Search，宽度优先搜索），因为BFS会更多地在当前节点的邻域中进行游走遍历，相当于对当前节点周边的网络结构进行一次“微观扫描”。当前节点是“局部中心节点”，还是“边缘节点”，亦或是“连接性节点”，其生成的序列包含的节点数量和顺序必然是不同的，从而让最终的Embedding抓取到更多结构性信息。

而为了表达“同质性”，随机游走要更倾向于DFS（Depth First Search，深度优先搜索）才行，因为DFS更有可能通过多次跳转，游走到远方的节点上。但无论怎样，DFS的游走更大概率会在一个大的集团内部进行，这就使得一个集团或者社区内部节点的Embedding更为相似，从而更多地表达网络的“同质性”。

那在Node2vec算法中，究竟是怎样控制BFS和DFS的倾向性的呢？

其实，它主要是通过节点间的跳转概率来控制跳转的倾向性。图4所示为Node2vec算法从节点t跳转到节点v后，再从节点v跳转到周围各点的跳转概率。这里，你要注意这几个节点的特点。比如，节点t是随机游走上一步访问的节点，节点v是当前访问的节点，节点x₁、x₂、x₃是与v相连的非t节点，但节点x₁还与节点t相连，这些不同的特点决定了随机游走时下一次跳转的概率。

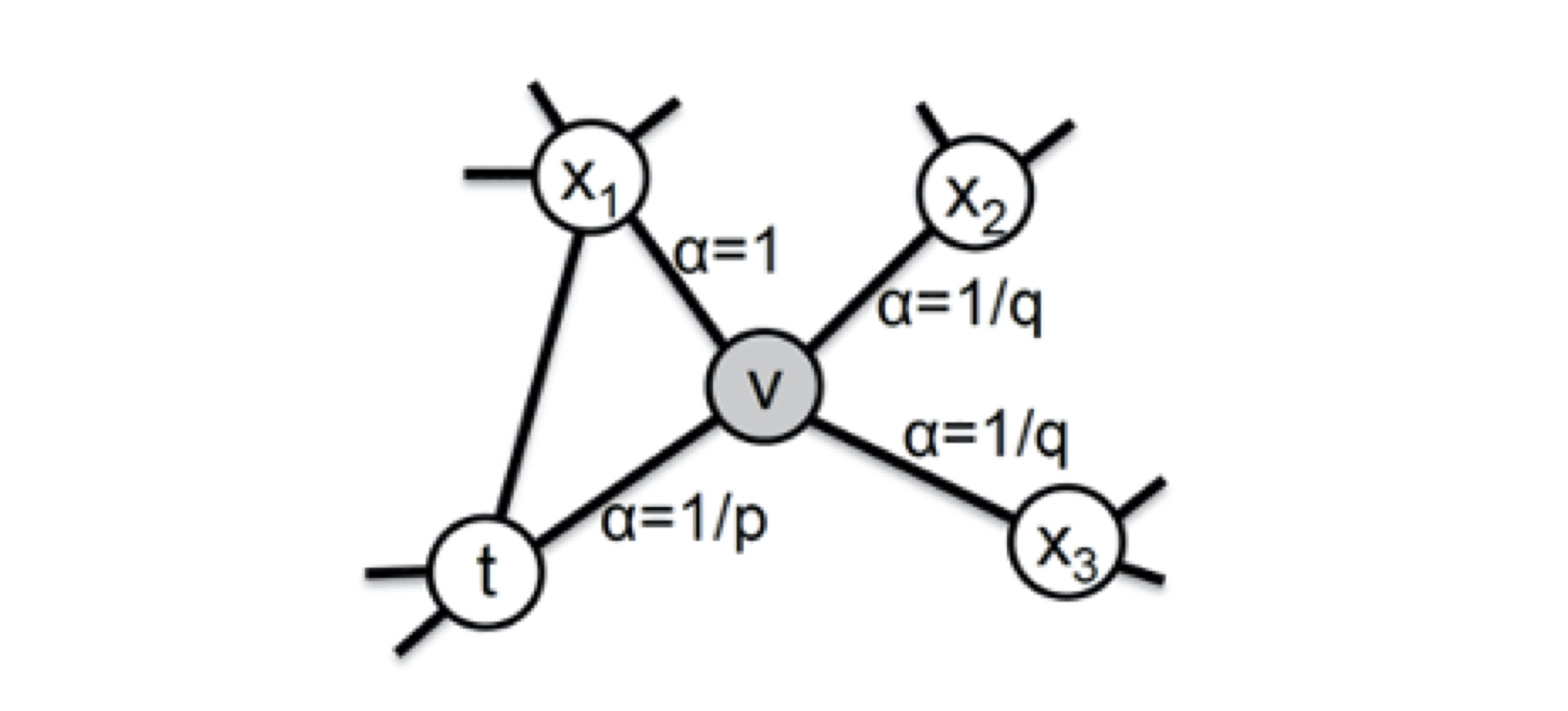
这些概率我们还可以用具体的公式来表示，从当前节点v跳转到下一个节点x的概率$\pi_{v x}=\alpha_{p q}(t, x) \cdot \omega_{v x}$ ，其中wvx是边vx的原始权重，$\alpha_{p q}(t, x)$是Node2vec定义的一个跳转权重。到底是倾向于DFS还是BFS，主要就与这个跳转权重的定义有关了。这里我们先了解一下它的精确定义，我再作进一步的解释：

$$\alpha_{p q(t, x)=}\left\{\begin{array}{ll}\frac{1}{p} & \text { 如果 } d_{t x}=0\\\ 1 & \text { 如果 } d_{t x}=1\\\frac{1}{q} & \text { 如果 } d_{t x}=2\end{array}\right.$$

$\alpha_{p q}(t, x)$里的d_tx是指节点t到节点x的距离，比如节点x₁其实是与节点t直接相连的，所以这个距离d_tx就是1，节点t到节点t自己的距离d_tt就是0，而x₂、x₃这些不与t相连的节点，d_tx就是2。

此外，$\alpha_{p q}(t, x)$中的参数p和q共同控制着随机游走的倾向性。参数p被称为返回参数（Return Parameter），p越小，随机游走回节点t的可能性越大，Node2vec就更注重表达网络的结构性。参数q被称为进出参数（In-out Parameter），q越小，随机游走到远方节点的可能性越大，Node2vec更注重表达网络的同质性。反之，当前节点更可能在附近节点游走。你可以自己尝试给p和q设置不同大小的值，算一算从v跳转到t、x₁、x₂和x₃的跳转概率。这样一来，应该就不难理解我刚才所说的随机游走倾向性的问题啦。

Node2vec这种灵活表达同质性和结构性的特点也得到了实验的证实，我们可以通过调整p和q参数让它产生不同的Embedding结果。图5上就是Node2vec更注重同质性的体现，从中我们可以看到，距离相近的节点颜色更为接近，图5下则是更注重结构性的体现，其中结构特点相近的节点的颜色更为接近。

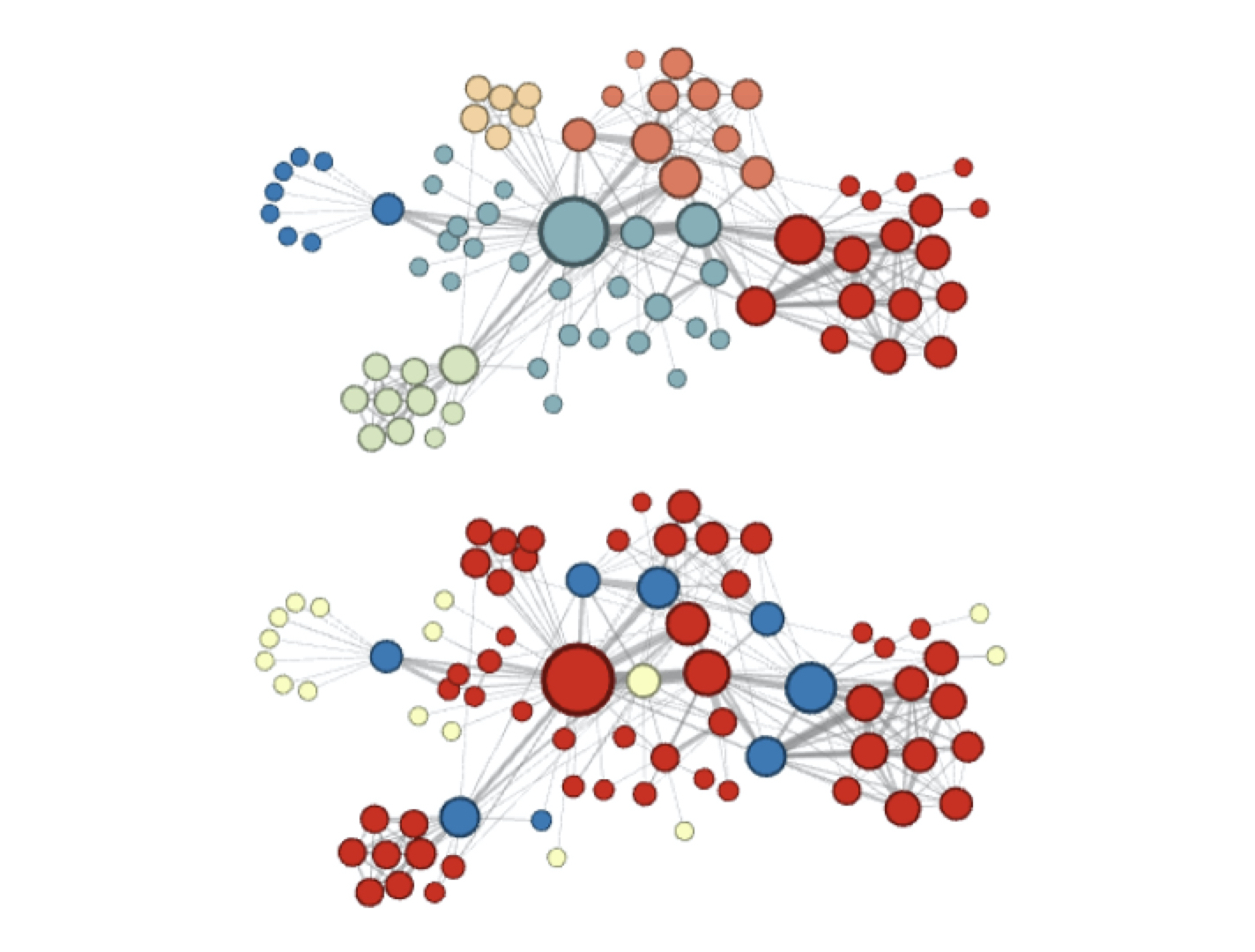
毫无疑问，Node2vec所体现的网络的同质性和结构性，在推荐系统中都是非常重要的特征表达。由于Node2vec的这种灵活性，以及发掘不同图特征的能力，我们甚至可以把不同Node2vec生成的偏向“结构性”的Embedding结果，以及偏向“同质性”的Embedding结果共同输入后续深度学习网络，以保留物品的不同图特征信息。

Embedding是如何应用在推荐系统的特征工程中的？

到这里，我们已经学习了好几种主流的Embedding方法，包括序列数据的Embedding方法，Word2vec和Item2vec，以及图数据的Embedding方法，Deep Walk和Node2vec。那你有没有想过，我为什么要在特征工程这一模块里介绍Embedding呢？Embedding又是怎么应用到推荐系统中的呢？这里，我就来做一个统一的解答。

第一个问题不难回答，由于Embedding的产出就是一个数值型特征向量，所以Embedding技术本身就可以视作特征处理方式的一种。只不过与简单的One-hot编码等方式不同，Embedding是一种更高阶的特征处理方法，它具备了把序列结构、网络结构、甚至其他特征融合到一个特征向量中的能力。

而第二个问题的答案有三个，因为Embedding在推荐系统中的应用方式大致有三种，分别是“直接应用”“预训练应用”和“End2End应用”。

其中，“直接应用”最简单，就是在我们得到Embedding向量之后，直接利用Embedding向量的相似性实现某些推荐系统的功能。典型的功能有，利用物品Embedding间的相似性实现相似物品推荐，利用物品Embedding和用户Embedding的相似性实现“猜你喜欢”等经典推荐功能，还可以利用物品Embedding实现推荐系统中的召回层等。当然，如果你还不熟悉这些应用细节，也完全不用担心，我们在之后的课程中都会讲到。

“预训练应用”指的是在我们预先训练好物品和用户的Embedding之后，不直接应用，而是把这些Embedding向量作为特征向量的一部分，跟其余的特征向量拼接起来，作为推荐模型的输入参与训练。这样做能够更好地把其他特征引入进来，让推荐模型作出更为全面且准确的预测。

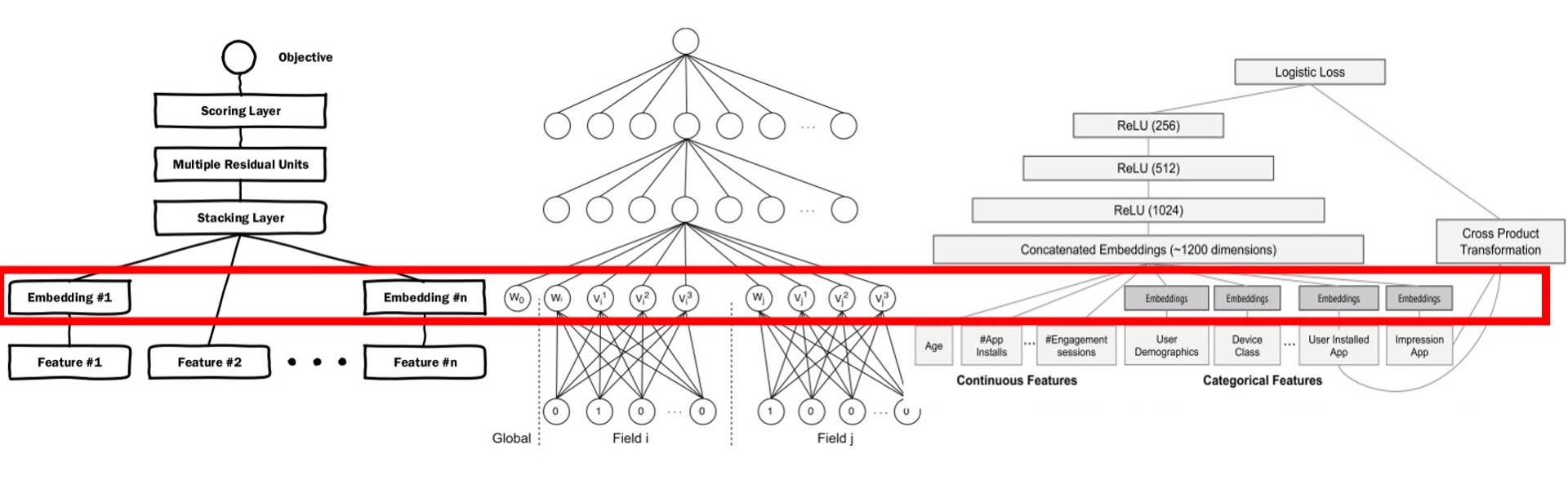
第三种应用叫做“End2End应用”。看上去这是个新的名词，它的全称叫做“End to End Training”，也就是端到端训练。不过，它其实并不神秘，就是指我们不预先训练Embedding，而是把Embedding的训练与深度学习推荐模型结合起来，采用统一的、端到端的方式一起训练，直接得到包含Embedding层的推荐模型。这种方式非常流行，比如图6就展示了三个包含Embedding层的经典模型，分别是微软的Deep Crossing，UCL提出的FNN和Google的Wide&Deep。它们的实现细节我们也会在后续课程里面介绍，你这里只需要了解这个概念就可以了。

小结

这节课我们一起学习了Graph Embedding的两种主要方法，分别是Deep Walk和Node2vec，并且我们还总结了Embedding技术在深度学习推荐系统中的应用方法。

学习Deep Walk方法关键在于理解它的算法流程，首先，我们基于原始的用户行为序列来构建物品关系图，然后采用随机游走的方式随机选择起始点，重新产生物品序列，最后将这些随机游走生成的物品序列输入Word2vec模型，生成最终的物品Embedding向量。

而Node2vec相比于Deep Walk，增加了随机游走过程中跳转概率的倾向性。如果倾向于宽度优先搜索，则Embedding结果更加体现“结构性”。如果倾向于深度优先搜索，则更加体现“同质性”。

最后，我们介绍了Embedding技术在深度学习推荐系统中的三种应用方法，“直接应用”“预训练”和“End2End训练”。这些方法各有特点，它们都是业界主流的应用方法，随着课程的不断深入，我会带你一步一步揭开它们的面纱。

老规矩，在课程的最后，我还是用表格的方式总结了这次课的关键知识点，你可以利用它来复习巩固。

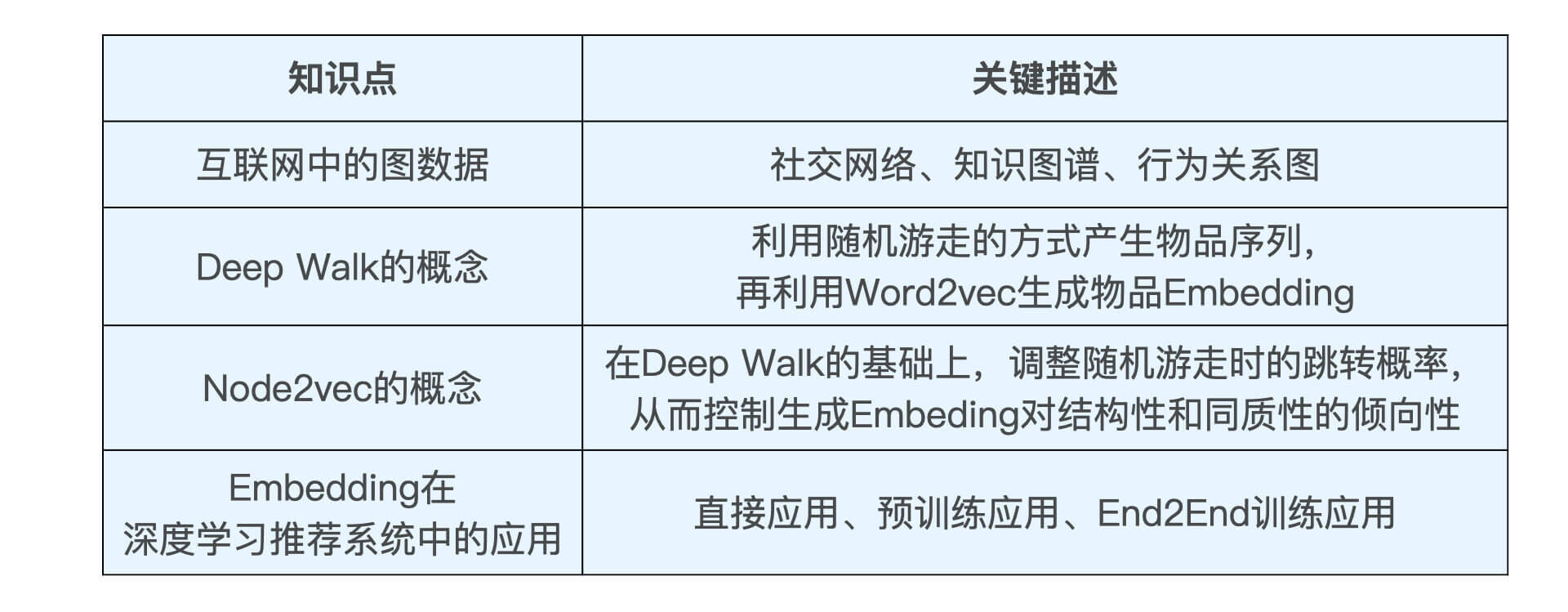
至此，我们就完成了所有Embedding理论部分的学习。下节课，我们再一起进入Embedding和Graph Embedding的实践部分，利用Sparrow Recsys的数据，使用Spark实现Embedding的训练，希望你到时能跟我一起动起手来！

课后思考

你能尝试对比一下Embedding预训练和Embedding End2End训练这两种应用方法，说出它们之间的优缺点吗？

欢迎在留言区分享你的思考和答案，如果这节Graph Embedding的课程让你有所收获，那不妨也把这节课分享给你的朋友们，我们下节课见！