你好，我是王喆。今天我们要开启推荐模型篇的学习。

推荐模型篇是整个课程中最重要的一个模块，因为推荐模型直接决定了最终物品排序的结果，它的好坏也直接影响着推荐效果的优劣。而且，从某种意义上讲，推荐系统的整体架构都是围绕着推荐模型搭建的，用于支持推荐模型的上线、训练、评估、服务。因此，我一直把推荐模型称作“推荐系统这个皇冠上的明珠”。

而提起推荐模型，我们就不能不提协同过滤算法。它可能是推荐系统自诞生以来最经典的算法，且没有之一。虽然我们课程的主题是“深度学习”推荐系统，但协同过滤以及它后续衍生出来的各类模型，都与深度学习推荐模型有着千丝万缕的联系。因此，在进入深度学习模型之前，掌握协同过滤及其衍生模型是非常有必要的。

今天，我就来给你讲讲经典协同过滤和它的衍生模型矩阵分解的原理，以及相关的Spark实现。

协同过滤算法的基本原理

我在特征工程篇曾经提到过：“用户行为数据是推荐系统最常用，也是最关键的数据。用户的潜在兴趣、用户对物品的评价好坏都反映在用户的行为历史中”。

而协同过滤算法，就是一种完全依赖用户和物品之间行为关系的推荐算法。我们从它的名字“协同过滤”中，也可以窥探到它背后的原理，就是 “协同大家的反馈、评价和意见一起对海量的信息进行过滤，从中筛选出用户可能感兴趣的信息”。

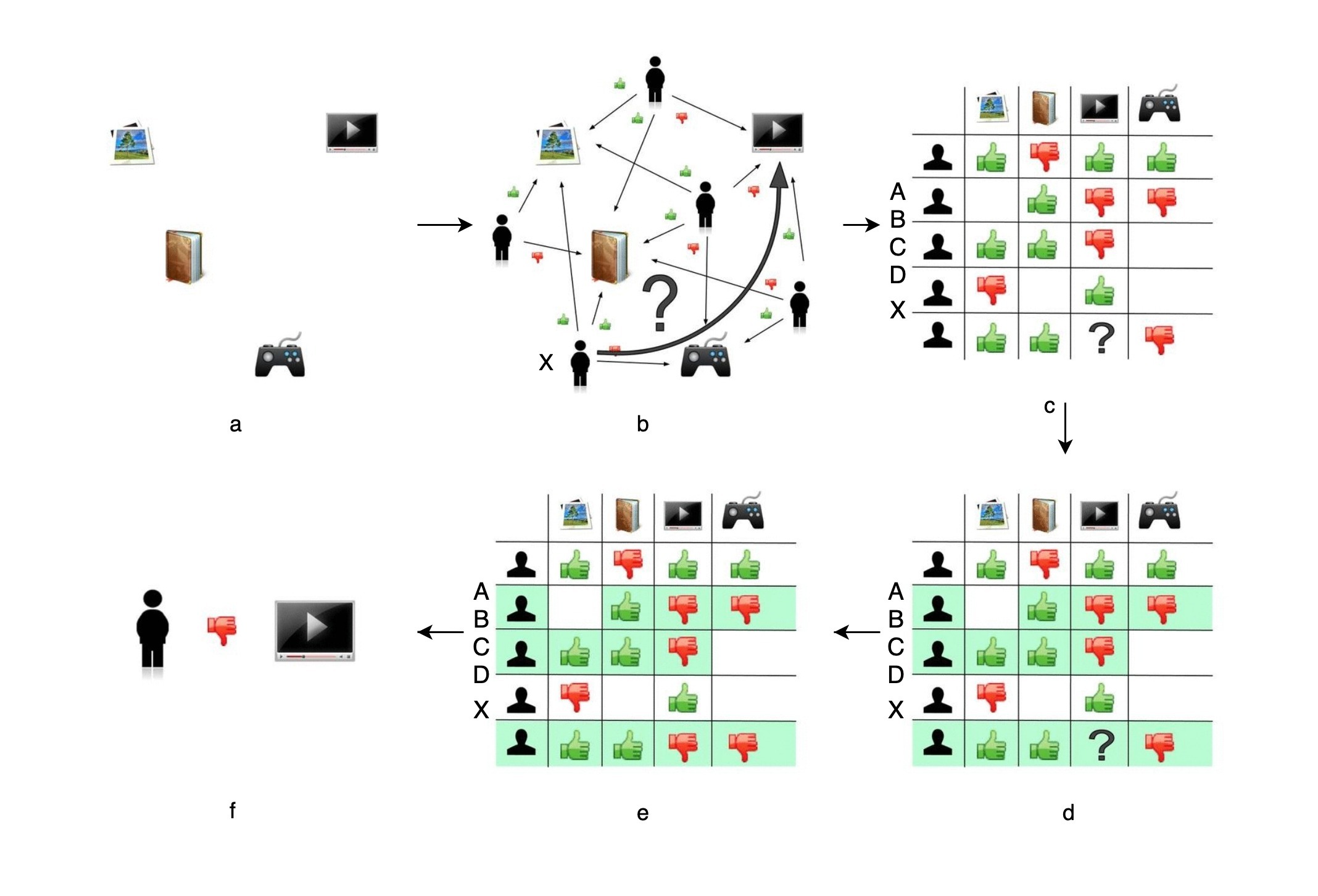
这么说可能还是太抽象了，接下来，我们就一起看一个电商场景下的例子。通过分析这个例子，你就能搞清楚协同过滤算法的推荐过程了。这个电商推荐系统从得到原始数据到生成最终推荐分数，全过程一共可以总结为6个步骤，如下所示。下面，我们一一来讲。

首先，我们可以看到，电商网站的商品库里一共有4件商品：一个游戏机、一本小说、一本杂志，以及一台电视机。假设，现在有一名用户X访问了这个电商网站，电商网站的推荐系统需要决定是否推荐电视机给用户X。

为了进行这项预测，推荐系统可以利用的数据有用户X对其他商品的历史评价数据，以及其他用户对这些商品的历史评价数据。我在图1(b)中用绿色“点赞”的标志表示好评，用红色“踩”的标志表示了差评。这样一来，用户、商品和评价记录就构成了带有标识的有向图。

接下来，为了方便计算，我们将有向图转换成矩阵的形式。这个矩阵表示了物品共同出现的情况，因此被称为“共现矩阵”。其中，用户作为矩阵行坐标，物品作为列坐标，我们再把“点赞”和“踩”的用户行为数据转换为矩阵中相应的元素值。这里，我们将“点赞”的值设为1，将“踩”的值设为-1，“没有数据”置为0（如果用户对物品有具体的评分，那么共现矩阵中的元素值可以取具体的评分值，没有数据时的默认评分也可以取评分的均值）。

你发现了吗，生成共现矩阵之后，推荐问题就转换成了预测矩阵中问号元素（图1(d)所示）的值的问题。由于在“协同”过滤算法中，推荐的原理是让用户考虑与自己兴趣相似用户的意见。因此，我们预测的第一步就是找到与用户X兴趣最相似的n（Top n用户，这里的n是一个超参数）个用户，然后综合相似用户对“电视机”的评价，得出用户X对“电视机”评价的预测。

从共现矩阵中我们可以知道，用户B和用户C由于跟用户X的行向量近似，被选为Top n（这里假设n取2）相似用户，接着在图1(e)中我们可以看到，用户B和用户C对“电视机”的评价均是负面的。因为相似用户对“电视机”的评价是负面的，所以我们可以预测出用户X对“电视机”的评价也是负面的。在实际的推荐过程中，推荐系统不会向用户X推荐“电视机”这一物品。

到这里，协同过滤的算法流程我们就说完了。也许你也已经发现了，这个过程中有两点不严谨的地方，一是用户相似度到底该怎么定义，二是最后我们预测用户X对“电视机”的评价也是负面的，这个负面程度应该有一个分数来衡量，但这个推荐分数该怎么计算呢？

计算用户相似度

首先，我们来解决计算用户相似度的问题。计算用户相似度其实并不是什么难事，因为在共现矩阵中，每个用户对应的行向量其实就可以当作一个用户的Embedding向量。相信你早已经熟悉Embedding相似度的计算方法，那我们这里依葫芦画瓢就可以知道基于共现矩阵的用户相似度计算方法啦。

最经典的方法就是利用余弦相似度了，它衡量了用户向量i和用户向量j之间的向量夹角大小。夹角越小，余弦相似度越大，两个用户越相似，它的定义如下：

除了最常用的余弦相似度之外，相似度的定义还有皮尔逊相关系数、欧式距离等等。咱们课程主要使用的是余弦相似度，因此你只要掌握它就可以了，其他的定义我这里不再多说了。

用户评分的预测

接下来，我们再来看看推荐分数的计算。在获得Top n个相似用户之后，利用Top n用户生成最终的用户$u$对物品$p$的评分是一个比较直接的过程。这里，我们假设的是“目标用户与其相似用户的喜好是相似的”，根据这个假设，我们可以利用相似用户的已有评价对目标用户的偏好进行预测。最常用的方式是，利用用户相似度和相似用户评价的加权平均值，来获得目标用户的评价预测，公式如下所示。

$$
\mathrm{R}_{u, p}=\frac{\sum_{s \epsilon S}\left(w_{u, s} \cdot R_{s, p}\right)}{\sum_{s \in S} w_{u, s}}
$$

其中，权重$w_{u, s}$是用户$u$和用户$s$的相似度，$R_{s, p}$ 是用户$s$对物品$p$的评分。

在获得用户$u$对不同物品的评价预测后，最终的推荐列表根据评价预测得分进行排序即可得到。到这里，我们就完成了协同过滤的全部推荐过程。

矩阵分解算法的原理

虽然说协同过滤是目前公认的最经典的推荐算法，但我们还是可以轻松找出它的缺点，那就是共现矩阵往往非常稀疏，在用户历史行为很少的情况下，寻找相似用户的过程并不准确。于是，著名的视频流媒体公司Netflix对协同过滤算法进行了改进，提出了矩阵分解算法，加强了模型处理稀疏矩阵的能力。

这里，我们还是用一个直观的例子来理解一下什么叫做矩阵分解。这次我从Netflix的矩阵分解论文中截取了两张示意图（图2），来比较协同过滤和矩阵分解的原理。

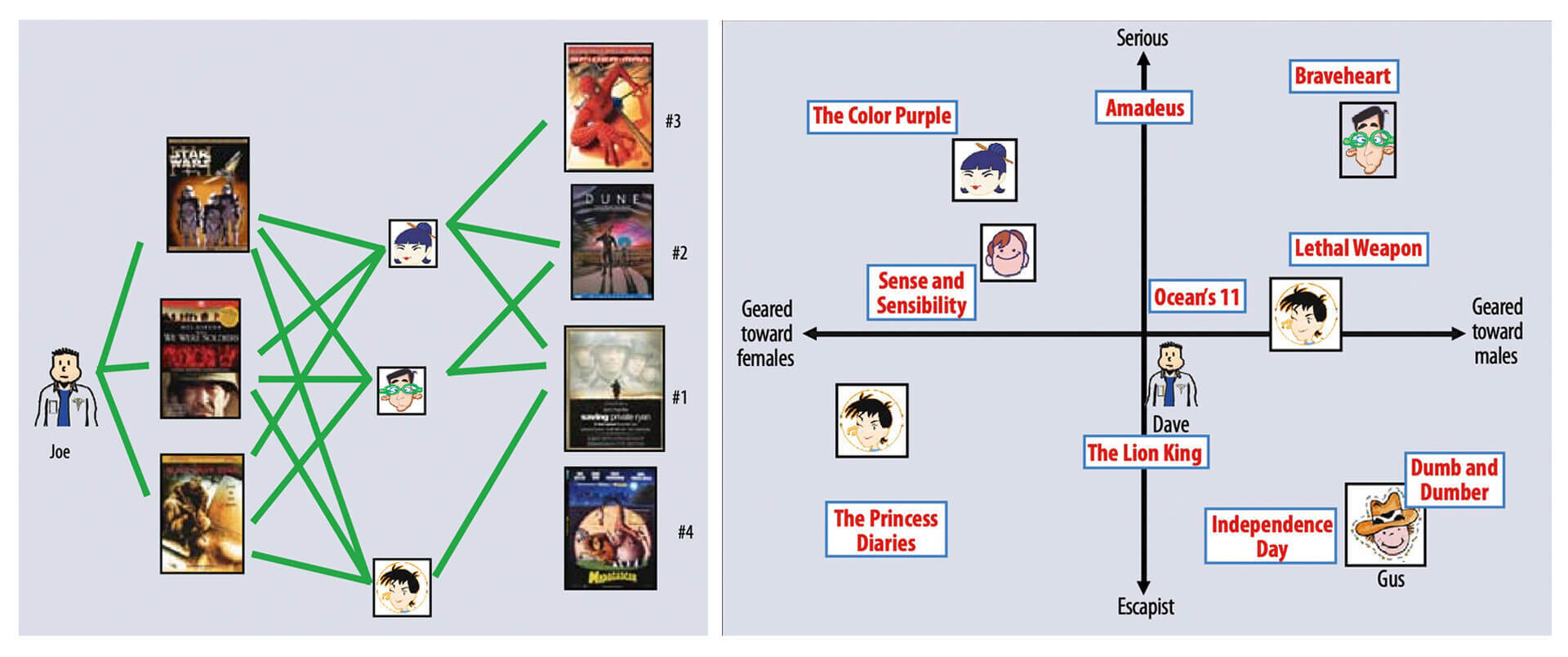
如图2(a)所示，协同过滤算法找到用户可能喜欢的视频的方式很直观，就是利用用户的观看历史，找到跟目标用户Joe看过同样视频的相似用户，然后找到这些相似用户喜欢看的其他视频，推荐给目标用户Joe。

矩阵分解算法则是期望为每一个用户和视频生成一个隐向量，将用户和视频定位到隐向量的表示空间上（如图2(b)所示），距离相近的用户和视频表明兴趣特点接近，在推荐过程中，我们就应该把距离相近的视频推荐给目标用户。例如，如果希望为图2(b)中的用户Dave推荐视频，我们可以找到离Dave的用户向量最近的两个视频向量，它们分别是《Ocean’s 11》和《The Lion King》，然后我们可以根据向量距离由近到远的顺序生成Dave的推荐列表。

这个时候你肯定觉得，矩阵分解不就是相当于一种Embedding方法嘛。没错，矩阵分解的主要过程，就是先分解协同过滤生成的共现矩阵，生成用户和物品的隐向量，再通过用户和物品隐向量间的相似性进行推荐。

那这个过程的关键就在于如何分解这个共现矩阵了。从形式上看，矩阵分解的过程是直观的，就是把一个mxn的共现矩阵，分解成一个mxk的用户矩阵和kxn的物品矩阵相乘的形式（如图3）。

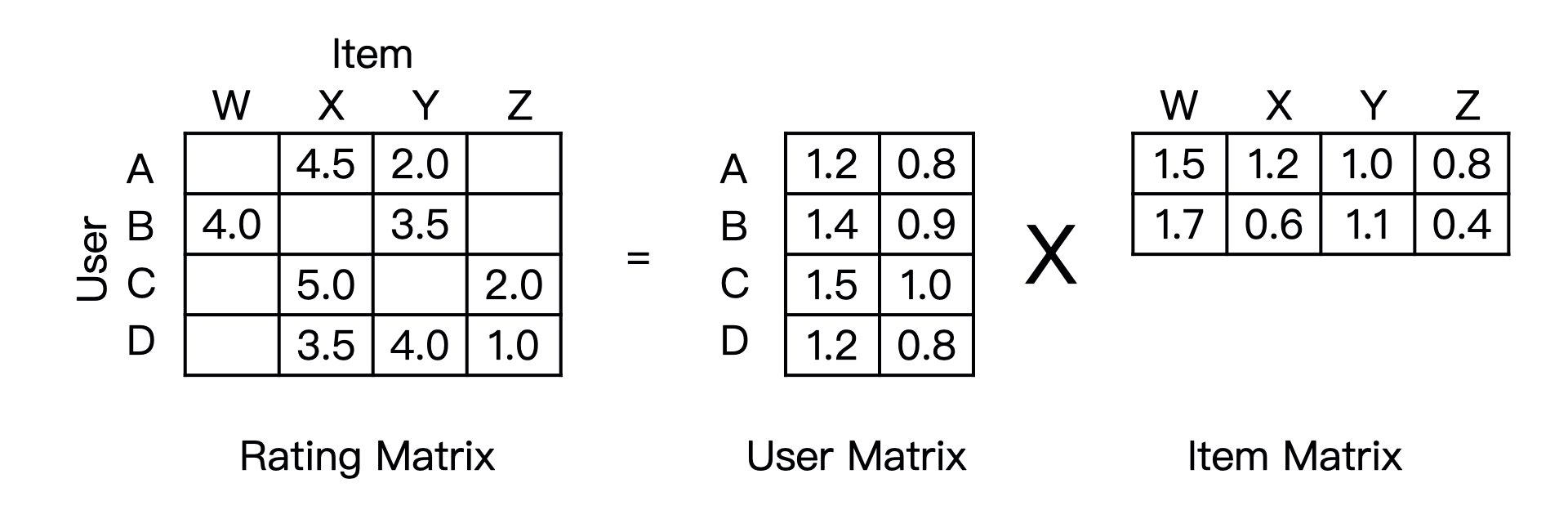
有了用户矩阵和物品矩阵，用户隐向量和物品隐向量就非常好提取了。用户隐向量就是用户矩阵相应的行向量，而物品隐向量就是物品矩阵相应的列向量。

那关键问题就剩下一个，也就是我们该通过什么方法把共现矩阵分解开呢？最常用的方法就是梯度下降。梯度下降的原理我们在第3讲学习过，简单来说就是通过求取偏导的形式来更新权重。梯度更新的公式是 $(w^{t+1}=w^{t}-\alpha * \frac{\partial L}{\partial w})$。为了实现梯度下降，最重要的一步是定义损失函数$L$，定义好损失函数我们才能够通过求导的方式找到梯度方向，这里我们就给出矩阵分解损失函数的定义如下。

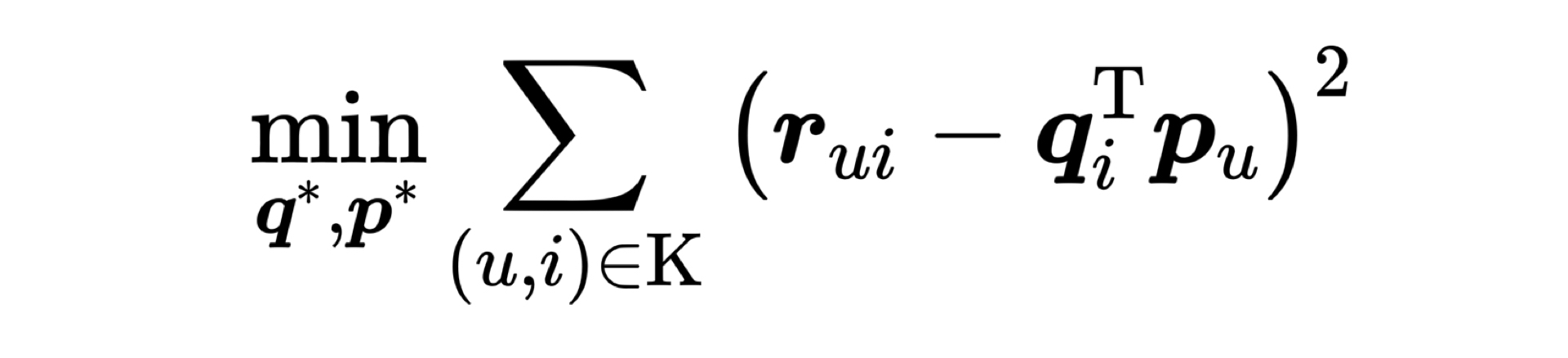
这个目标函数里面，${r}_{u i}$ 是共现矩阵里面用户$u$对物品$i$的评分，${q}_{i}$ 是物品向量，${p}_{u}$ 是用户向量，K是所有用户评分物品的全体集合。通过目标函数的定义我们可以看到，我们要求的物品向量和用户向量，是希望让物品向量和用户向量之积跟原始的评分之差的平方尽量小。简单来说就是，我们希望用户矩阵和物品矩阵的乘积尽量接近原来的共现矩阵。

在通过训练得到用户隐向量和物品隐向量之后，在服务器内部的推荐过程跟我们之前讲过的Embedding推荐是一样的，你也已经在Sparrow RecSys里面实践过，是这方面的专家了，我就不再多说了。

矩阵分解算法的Spark实现

基础知识学完，接下来又到了show me the code时间了。这里，我们继续使用Spark实现矩阵分解算法，我会结合下面的关键代码一起来讲。

我们可以看到，因为Spark MLlib已经帮我们封装好了模型，所以矩阵分解算法实现起来非常简单，还是通过我们熟悉的三步来完成，分别是定义模型，使用fit函数训练模型，提取物品和用户向量。

但是有一点我们需要注意，就是在模型中，我们需要在模型中指定训练样本中用户ID对应的列userIdInt和物品ID对应的列movieIdInt，并且两个ID列对应的数据类型需要是int类型的。

// 建立矩阵分解模型
val als = new ALS()
  .setMaxIter(5)
  .setRegParam(0.01)
  .setUserCol("userIdInt")
  .setItemCol("movieIdInt")
  .setRatingCol("ratingFloat")


//训练模型
val model = als.fit(training)


//得到物品向量和用户向量
model.itemFactors.show(10, truncate = false)
model.userFactors.show(10, truncate = false

其实，矩阵分解算法得出的结果，你完全可以把它当作Embedding来处理。具体怎么做呢？在讲Redis的时候，我们就已经实现过物品Embedding和用户Embedding的存储和线上预估的过程了，你可以直接参考它。最后，我建议你利用矩阵分解后的用户和物品隐向量，仿照其他Embedding的实现，在Sparrow RecSys中动手实现一下线上部署的过程，这样你就可以看到矩阵分解模型的实际效果了。

小结

这节课我们一起学习了协同过滤算法，以及它的后续算法矩阵分解，它是最经典的推荐算法。

总结来说，协同过滤是一种协同大家的反馈、评价和意见，对海量的信息进行过滤，从中筛选出用户感兴趣信息的一种推荐算法。它的实现过程主要有三步，先根据用户行为历史创建共现矩阵，然后根据共现矩阵查找相似用户，再根据相似用户喜欢的物品，推荐目标用户喜欢的物品。

但是协同过滤处理稀疏矩阵的能力比较差，因此，矩阵分解算法被提出了，它通过分解共现矩阵，生成用户向量矩阵和物品向量矩阵，进而得到用户隐向量和物品隐向量。你可以完全把最后的结果当作用户Embedding和物品Embedding来处理。

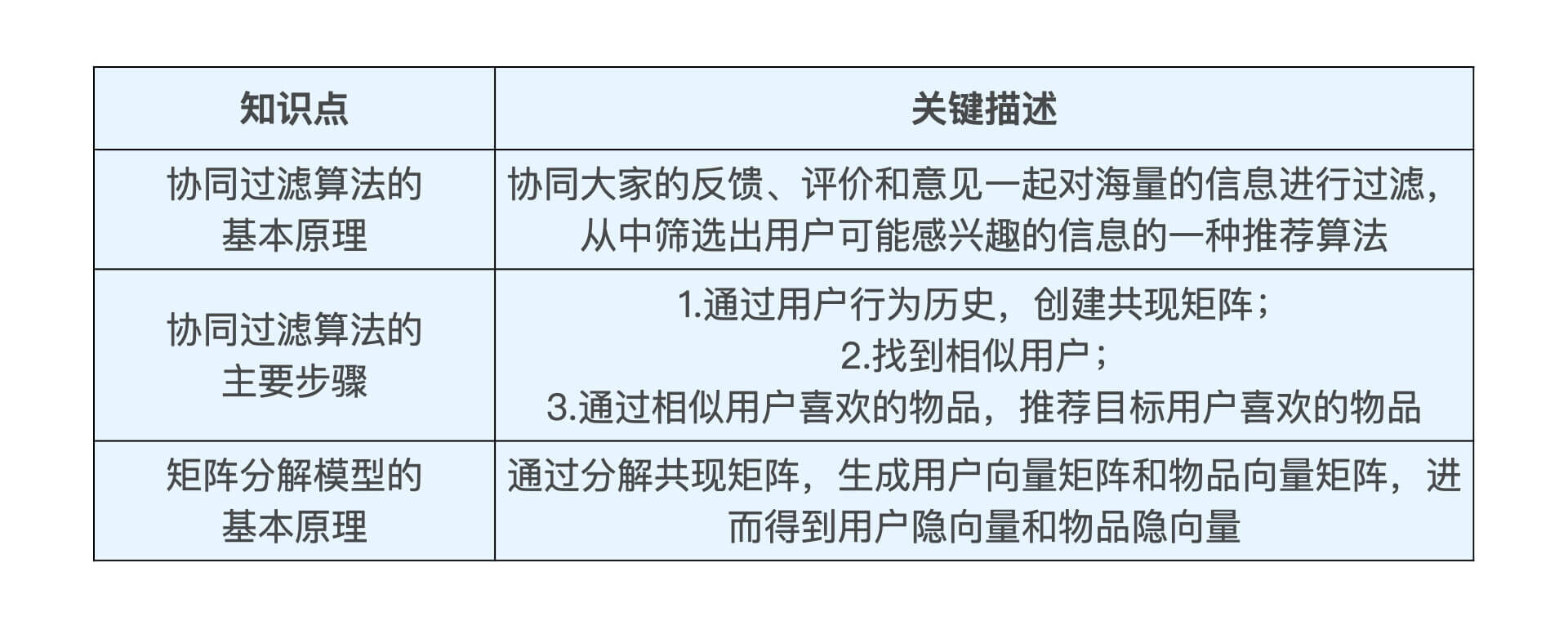
针对这节课的重要知识点，我把它们都列在了下面的表格里，你可以看看。

课后思考

1.基于协同过滤算法，你能找到进行相似“物品”推荐的方法吗？

2.在MovieLens数据集中，不同用户对物品打分的标准不尽相同。比如说，有的人可能爱打高分，评价的影片得分都在4分以上，有的人爱打低分，大部分影片都在3分以下。你觉得这样的偏好对于推荐结果有影响吗？我们能不能在算法中消除这种偏好呢？

关于矩阵分解算法的实现你学会了吗？欢迎把你的疑问和思考分享到留言区，也欢迎你能把这节课转发出去，我们下节课见！