你好,我是大圣。上一讲我们仔细分析了Vue中虚拟DOM如何执行的,整体流程就是树形结构的diff计算,但是在diff的计算过程中,如何高效计算虚拟DOM属性的变化,以及如何更新数组的子元素,需要一些算法知识的补充。
给你提前划个重点,今天我们将讲到如何使用位运算来实现Vue中的按需更新,让静态的节点可以越过虚拟DOM的计算逻辑,并且使用计算最长递增子序列的方式,来实现队伍的高效排序。我们会剖析Vue框架源码,结合对应的LeetCode题,帮助你掌握算法的核心原理和实现。
前面也复习了,在执行diff之前,要根据需要判断每个虚拟DOM节点有哪些属性需要计算,因为无论响应式数据怎么变化,静态的属性和节点都不会发生变化。
所以我们看每个节点diff的时候会做什么,在renderer.ts代码文件中就可以看到代码,主要就是通过虚拟DOM节点的patchFlag树形判断是否需要更新节点。
方法就是使用&操作符来判断操作的类型,比如patchFlag & PatchFlags.CLASS来判断当前元素的class是否需要计算diff;shapeFlag & ShapeFlags.ELEMENT来判断当前虚拟DOM是HTML元素还是Component组件。这个“&”其实就是位运算的按位与。
// class
// this flag is matched when the element has dynamic class bindings.
if (patchFlag & PatchFlags.CLASS) {
if (oldProps.class !== newProps.class) {
hostPatchProp(el, 'class', null, newProps.class, isSVG)
}
}
// style
// this flag is matched when the element has dynamic style bindings
if (patchFlag & PatchFlags.STYLE) {
hostPatchProp(el, 'style', oldProps.style, newProps.style, isSVG)
}
if (shapeFlag & ShapeFlags.ELEMENT) {
processElement(
n1,
n2,
container,
anchor,
parentComponent,
parentSuspense,
isSVG,
slotScopeIds,
optimized
)
} else if (shapeFlag & ShapeFlags.COMPONENT) {
processComponent(
n1,
n2,
container,
anchor,
parentComponent,
parentSuspense,
isSVG,
slotScopeIds,
optimized
)
}
上面的代码中 & 就是按位与的操作符,这其实是二进制上的计算符号,所以我们首先要了解一下什么是二进制。
我们日常使用的数字都是十进制数字,比如数字13就是 1*10+3 的运算结果,每个位置都是代表10的n次方。13也可以使用二进制表达,因为二进制每个位置只能是0和1两个数字,每个位置代表的是2的n次方,13在二进制里是1101,就是1*8+1*4+0*2+1*1。
而在JavaScript中我们可以很方便地使用toString(2)的方式,把十进制数字转换成二进制。运算的概念很简单,就是在二进制上的“与”和“或”运算:
(13).toString(2) // 1101
0 & 0 // 0
0 & 1 // 0
1 & 0 // 0
1 & 1 // 1
0 | 0 // 0
0 | 1 // 1
1 | 0 // 1
1 | 1 // 1
1 << 2 // 1左移动两位,就是100 就是1*2平方 = 4
二进制中,我们每个位置只能是0或者1这两个值,&和 | 的概念和JavaScript中的&&和 || 保持一致。两个二进制的&运算就是只有两个二进制位置都是1的时候,结果是1,其余情况运算结果都是0;| 是按位置进行“或”运算,只有两个二进制位置都是0的时候,结果是0,其余情况运算结果都是1;并且,还可以通过左移<< 和右移>>操作符,实现乘以2和除以2的效果。
由于这些都是在二进制上的计算,运算的性能通常会比字符串和数字的计算性能要好,这也是很多框架内部使用位运算的原因。
这么说估计你不是很理解,我们结合一个LeetCode题看看为什么说二进制的位运算性能更好。
我们来做一下LeetCode231题,题目描述很简单,判断数字n是不是2的幂次方,也就是说,判断数字n是不是2的整次方,比如2、4、8。我们可以很轻松地写出JavaScript的解答,n一直除以2,如果有余数就是false,否则就是true:
var isPowerOfTwo = function(n) {
if(n === 1) return true
while( n > 2 ){
n = n / 2
if(n % 2 !== 0) return false
}
return n===2
};
不过上面的解答我们可以用位运算来优化。
先来分析一下2的幂次方的特点。
2的幂次方就是数字1左移动若干次,其余位置全部都是0,所以n-1就是最高位变成0,其余位置都变成1,就像十进制里的10000-1 = 9999。这样,n和n-1每个二进制位的数字都不一样,我们可以很轻松地用按位“与”来判断这个题的答案,如果n&n-1是0的话,数字n就符合2的整次幂的特点:
16
10000
16-1 = 15
01111
16&15 == 0
var isPowerOfTwo = function(n) {
return n>0 && (n & (n - 1)) === 0
};
所以我们使用位运算提高了代码的整体性能。
好,搞清楚为什么用位运算,我们回来看diff判断,如何根据位运算的特点,设计出权限的组合认证方案。
比如Vue中的动态属性,有文本、class、style、props几个属性,我们可以使用二进制中的一个位置来表示权限,看下面的代码,我们使用左移的方式分别在四个二进制上标记了1,代表四种不同的权限,使用按位或的方式去实现权限授予。
比如,一个节点如果TEXT和STYLE都需要修改,我们只需要使用 | 运算符就可以得到flag1的权限表示,这就是为什么Vue 3 中针对虚拟DOM类型以及虚拟DOM需要动态计算diff的树形都做了标记,你可以在Vue 3的源码中看到下面的配置:
const PatchFlags = {
TEXT:1, // 0001
CLASS: 1<<1, // 0010
STYLE:1<<2, // 0100
PROPS:1<<3 // 1000
}
const flag1 = PatchFlags.TEXT | PatchFlags.STYLE // 0101
// 权限校验
flag1 & PatchFlags.TEXT // 有权限,结果大于1
flag1 & PatchFlags.CLASS //没有权限 是0
然后就到了今天的重点:我们虚拟DOM计算diff中的算法了。
上一讲我们详细介绍了在虚拟diff计算中,如果新老子元素都是数组的时候,需要先做首尾的预判,如果新的子元素和老的子元素在预判完毕后,未处理的元素依然是数组,那么就需要对两个数组计算diff,最终找到最短的操作路径,能够让老的子元素通过尽可能少的操作,更新成为新的子元素。
Vue 3借鉴了infero的算法逻辑,就像操场上需要按照个头从低到高站好一样,我们采用的思路是先寻找一个现有队列中由低到高的队列,让这个队列尽可能的长,它们的相对位置不需要变化,而其他元素进行插入和移动位置,这样就可以做到尽可能少的操作DOM。
所以如何寻找这个最长递增的序列呢?这就是今天的重点算法知识了,我们看LeetCode第300题,题目描述如下, 需要在数组中找到最长底层的自序列长度:
给你一个整数数组 nums,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。
例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
=
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
首先我们可以使用动态规划的思路,通过每一步的递推,使用dp数组,记录出每一步操作的最优解,最后得到全局最优解。
在这个例子中,我们可以把dp[i]定义成nums[0]到nums[i]这个区间内,数组的最长递增子序列的长度,并且dp数组的初始值设为1。
从左边向右递推,如果nums[i+1]>nums[i],dp[i+1]就等于dp[i]+1;如果nums[i+1]<nums[i],就什么都不需要干,这样我们在遍历的过程中,就能根据数组当前位置之前的最长递增子序列长度推导出i+1位置的最长递增子序列长度。
所以可以得到如下解法:
/**
* @param {number[]} nums
* @return {number}
*/
const lengthOfLIS = function(nums) {
let n = nums.length;
if (n == 0) {
return 0;
}
let dp = new Array(n).fill(1);
for (let i = 0; i < n; i++) {
for (let j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return Math.max(...dp)
}
由于我们需要两层循环,所以这个解法的时间复杂度是n的平方,这个解法其实已经不错了,但是还有更优秀的解法,也就是Vue 3中用到的算法:贪心+二分。
我们再看一下这个题,贪心的思路就是在寻找最长递增的序列,所以,[1,3]要比[1,5]好,也就是说,在这个上升的序列中,我们要让上升速度尽可能变得慢,这样才有可能让后面的元素尽可能也递增。
我们可以创建一个arr数组,用来保存这种策略下的最长递增子序列。
如果当前遍历的nums[i]大于arr的最后一个元素,也就是大于arr的最大值时,我们把nums[i]追加到后面即可,否则我们就在arr中寻找一个第一个大于num[i]的数字并替换它。因为是arr是递增的数列,所以在寻找插入位置的时候,我们可以使用二分查找的方式,把整个算法的复杂度变成O(nlgn)。
下面的代码就是贪心+二分的解法,我们可以得到正确的最长递增子序列的长度:
/**
* @param {number[]} nums
* @return {number}
*/
const lengthOfLIS = function(nums) {
let len = nums.length
if (len <= 1) {
return len
}
let arr = [nums[0]]
for (let i = 0; i < len; i++) {
// nums[i] 大于 arr 尾元素时,直接追加到后面,递增序列长度+1
if (nums[i] > arr[arr.length - 1]) {
arr.push(nums[i])
} else {
// 否则,查找递增子序列中第一个大于numsp[i]的元素 替换它
// 递增序列,可以使用二分查找
let left = 0
let right = arr.length - 1
while (left < right) {
let mid = (left + right) >> 1
if (arr[mid] < nums[i]) {
left = mid + 1
} else {
right = mid
}
}
arr[left] = nums[i]
}
}
return arr.length
};
但是贪心+二分的这种解法,现在只能得到最长递增子序列的长度,但是最后得到的arr并不一定是最长递增子序列,因为我们移动的num[i]位置可能会不正确,只是得到的数组长度是正确的,所以我们需要对这个算法改造一下,把整个数组复制一份之后,最后也能得到正确的最长递增子序列。
具体代码怎么写呢?我们来到Vue 3的renderer.ts文件中,函数getSquenece就是用来生成最长递增子序列,看下面的代码:
// https://en.wikipedia.org/wiki/Longest_increasing_subsequence
function getSequence(arr: number[]): number[] {
const p = arr.slice() //赋值一份arr
const result = [0]
let i, j, u, v, c
const len = arr.length
for (i = 0; i < len; i++) {
const arrI = arr[i]
if (arrI !== 0) {
j = result[result.length - 1]
if (arr[j] < arrI) {
p[i] = j // 存储在result最后一个索引的值
result.push(i)
continue
}
u = 0
v = result.length - 1
// 二分查找,查找比arrI小的节点,更新result的值
while (u < v) {
c = (u + v) >> 1
if (arr[result[c]] < arrI) {
u = c + 1
} else {
v = c
}
}
if (arrI < arr[result[u]]) {
if (u > 0) {
p[i] = result[u - 1]
}
result[u] = i
}
}
}
u = result.length
v = result[u - 1]
// 查找数组p 找到最终的索引
while (u-- > 0) {
result[u] = v
v = p[v]
}
return result
}
这段代码就是Vue 3里的实现,result存储的就是长度是i的递增子序列最小末位置的索引,最后计算出最长递增子序列。
我们得到increasingNewIndexSequence队列后,再去遍历数组进行patch操作就可以实现完整的diff流程了:
for (i = toBePatched - 1; i >= 0; i--) {
const nextIndex = s2 + i
const nextChild = c2[nextIndex] as VNode
const anchor =
nextIndex + 1 < l2 ? (c2[nextIndex + 1] as VNode).el : parentAnchor
if (newIndexToOldIndexMap[i] === 0) {
// mount new
patch(
null,
nextChild,
container,
anchor,
parentComponent,
parentSuspense,
isSVG,
slotScopeIds,
optimized
)
} else if (moved) {
// move if:
// There is no stable subsequence (e.g. a reverse)
// OR current node is not among the stable sequence
if (j < 0 || i !== increasingNewIndexSequence[j]) {
move(nextChild, container, anchor, MoveType.REORDER)
} else {
j--
}
}
}
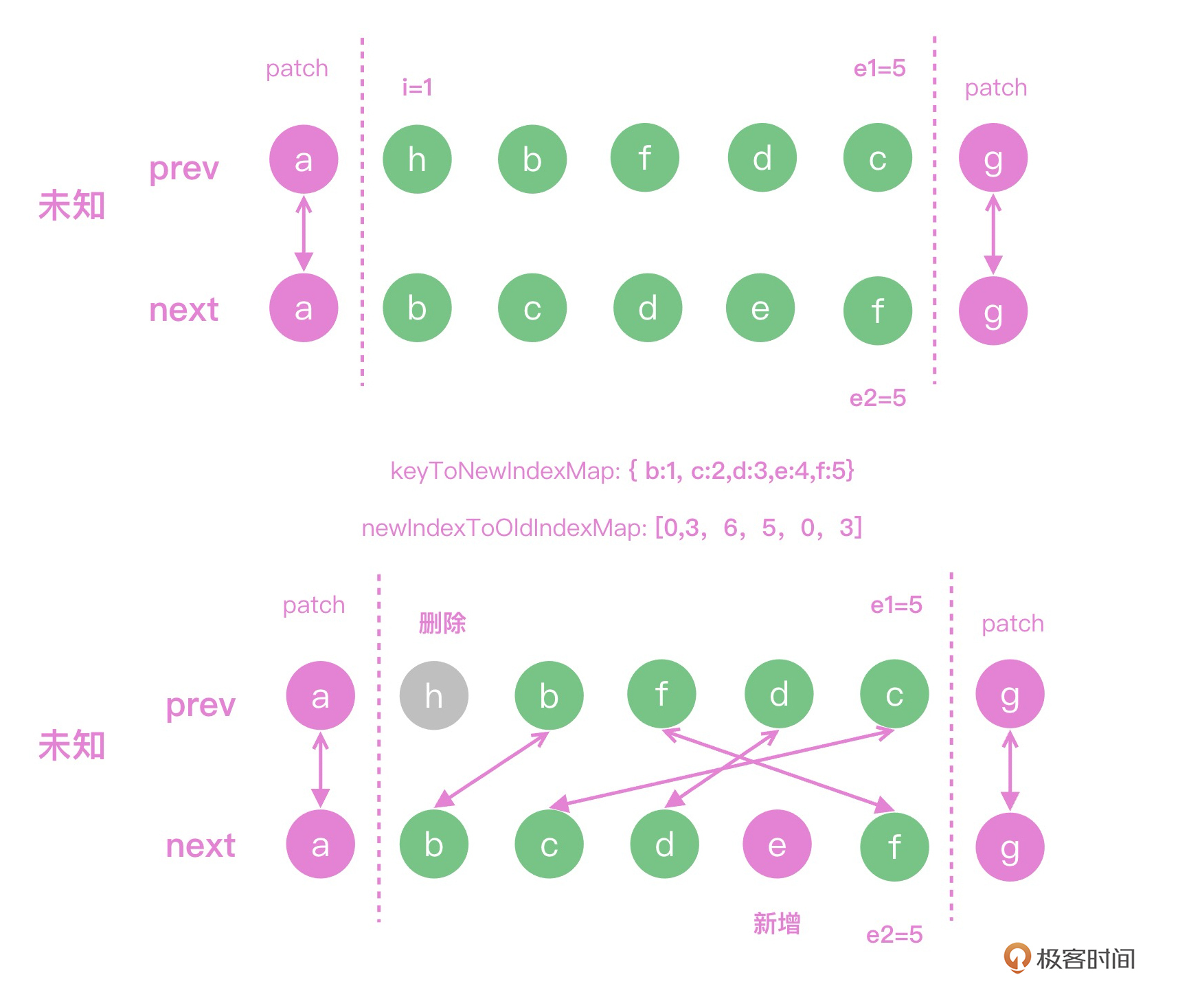
上面代码的思路,我们用下图演示。做完双端对比之后,a和g已经计算出可以直接复用DOM,剩下的队列中我们需要把hbfdc更新成abdef。
首先我们需要使用keyToNewIndexMap存储新节点中每个key对应的索引,比如下图中key是c的元素的索引就是2;然后计算出newIndexOldIndexMap存储这个key在老的子元素中的位置,我们可以根据c的索引是2,在newIndexOldIndexMap中查询到在老的子元素的位置是6, 关于newIndexOldIndexMap的具体逻辑你可以在上面的代码中看到:

今天的内容到这就结束了,对照着Vue执行全景图,我们回顾一下讲到的知识点。
首先我们分析了Vue 3中虚拟DOM diff中的静态标记功能,标记后通过位运算,可以快速判断出一个节点的类型是HTML标签还是Vue组件,然后去执行不同的操作方法;在节点更新的流程中,也可以通过位运算的方式确定需要更新的范围。
位运算就是通过二进制上的与和或运算,能够高效地进行权限的判断,我们在工作中如果涉及权限的判断,也可以借鉴类似的思路,Linux中的读写权限也是通过位运算的方式来实现的。
然后我们剖析了Vue的虚拟DOM中最为复杂的最长递增子序列算法,通过对LeetCode第300的题分析掌握了动态规划和贪心+二分的解法。
掌握算法思想之后,我们再回到Vue3的源码中分析代码的实现逻辑,patchKeyedChildren的核心逻辑就是在进行双端对比后,对无法预判的序列计算出最长递增子序列之后,我们通过编译数组,对其余的元素进行patch或者move的操作,完整实现了虚拟DOM 的diff。
学到这里相信你已经完全搞懂了虚拟DOM的执行,以及关键的diff操作思路,可以体会到Vue中极致的优化理念,使用位运算对Vue中的动态属性和节点进行标记,实现高效判断;对于两个数组的diff计算使用了最长递增子序列算法实现,优化了diff的时间复杂度。这也是为什么我一直建议刚入行的前端工程师要好好学习算法的主要原因。
最后给你留个思考题,你现在的项目中有哪些地方能用到位运算的地方呢?欢迎在评论去留言分享你的想法,我们下一讲再见。