
你好,我是微扰君。
上一讲我们学习了谷歌三架马车之一 MapReduce。建立在Google File System的基础上,MapReduce很好地解决了谷歌当时的大规模分布式计算问题,让业务工程师不再需要处理和分布式计算相关的容错、数据分发、计算调度等复杂的技术细节,而把精力放在业务问题本身。
不过谷歌作为一家搜索引擎公司,搜索自然是谷歌重中之重的核心业务。今天我们就来学习谷歌三架马车之二——PageRank算法。
早期的搜索引擎一般只是基于关键字进行匹配,按照匹配情况,把爬虫爬到的全部内容,再基于时间顺序进行排列,如果对搜索质量的把控高一点,可能最多也就是做到基于关键词出现频次的排序。但是,这样搜索出来的质量往往不是很让我们满意,而且容易出现站点作弊的情况,比如通过大量在网页内容中填充某些关键词,以提高自己的网页排名。
为了让用户获得更好的搜索体验从而打败竞争对手,谷歌是如何设计自己计算网页排名的算法的呢?
这就要提到PageRank算法,由谷歌创始人也是斯坦福大学的博士生 Larry Page 提出的,算法既以Larry Page本人名字来命名,同时也包含了网页排名的意义。 PageRank 算法不止可以让用户搜索到自己关心的内容,也往往能让质量更高的网页得以排到更前的位置,同时它也是一个典型的 MapReduce 的应用场景。
那 PageRank 具体是怎么做网页排名的呢?
其实这里面的想法主要受到了论文影响力因子的启发;在学术网络中论文的影响力因子往往是基于论文被引用次数来衡量的,这是一种最简单也非常有效的评价指标。
一篇影响广泛的论文,往往会成为许多其他工作的基础,从而收获大量的引用。以1998年发布的PageRank这篇论文本身为例,到现在一共收获了16102次引用,足以说明这是一篇非常有影响力的工作。

有相当多的学者在用图的方法研究学术网络中的问题,如果你把论文看成图,那么论文之间的引用关系就是一条条有向边,入边越多的节点,影响力一般来说也越高。
网页和学术论文其实在有些方面是很像的。如果把网页看成图上的节点,由于网页之间有一些超链接指向,谷歌所能爬到的所有网页就会构成一张类似于学术网络的图。
PageRank 对网页的排名,本质上也是这样一种基于引用情况和影响力的排名。背后的逻辑很简单,被更多超链接指向的网页,可以推断它往往会有更好的质量,因为当时许多HomePage类的导航网站都会链接到一些提供优质服务的网站,如果一个网站质量很差,自然也不会被太多链接所指向。
那简单统计引用次数,也就是我们把爬到的那些在网络中被链接次数更多的网页排到更前面,行不行呢?
这样当然也一定程度上可以反映出网页的排名情况,但不同网站的链接所代表的权重应该是不同的。比如雅虎链接的网页和某个个人主页所链接的网页,显然代表的意义是不同的,如果把所有的引用都看成权重一样的,并不令人满意,而且也很容易作弊。只要建立大量的网页,链接向某个想要在搜索引擎中提高权重的网页,在只看引用次数的算法下,很容易就把网页排名提高了。
Larry Page 的PageRank算法考虑到了不同链接的权重,整个过程也非常简单容易理解。
我们先按照他论文中的数学语言描述一下整个网页集合,方便后面分析。假设u代表了某一个网页;$F_u$代表u所指向的网页集合,$N_u$代表$F_u$集合的大小;$B_u$代表指向u的网页集合;c是一个因子,用来保持所有网页权重之和是一个常数。
如果我们用 R(u) 表示网页u的权重,拉里佩奇是这样计算权重的:
$$R(u)=\sum_{v\subset B_u}R(v)/(N_v)$$
光看数学公式不是很好理解,我们对照这个图片来看:
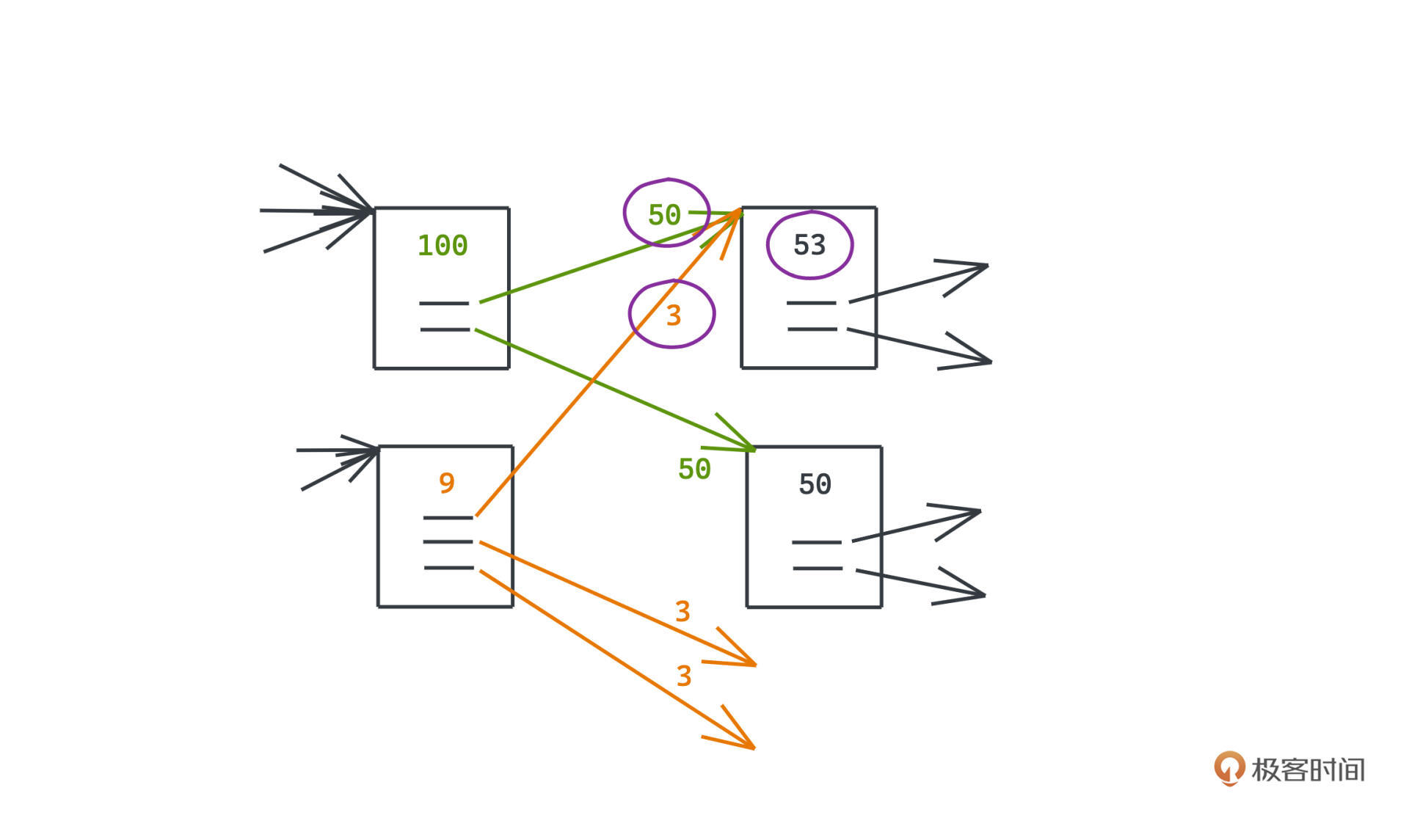
每个网页都有不同的权重用来排名,如何计算这个权重呢?拉里佩奇的做法就是对指向当前页面的所有页面,我们直接它们的权重做某种程度上的加权平均。
每个页面的总体权重会被平均分散到它所指向的页面中去,比如图中权重为100的网页,有两条出边,那么每条边的权重就会记录为50。那么对于被指向的网页权重如何计算呢?比如权重为53的网页,就是用指向它的两条链接的权重,进行累计求和,也就是50+3=53。
这样的分配是简单而有效的。因为我们可以简化地认为用户从某个网页跳转到另一个网页的概率,就是在当前网页的所有超链接中,随机选择一个,进行跳转,那当前网页的影响力被平均地转移到它所指向的网页,也是很符合直觉的。
但是这样的计算方式显然是动态的、迭代的,每一轮迭代计算的结果都依赖上一轮迭代的结果,所以它们看起来都会依赖整个图的初始状态,我们如何初始化权重呢?
其实无论怎么初始化权重,最终都会趋于平稳。数学上这个问题被称为马氏链平稳状态定理,我们大致了解一下,只要所有状态之间都是互相可达,且整个转移过程没有周期性。那么无论如何初始化,只要状态转移矩阵是确定的,最终整个马氏链一定会趋于稳定。背后的数学就不仔细展开讲解了,你感兴趣的话可以自己搜索了解一下。
我们用一个论文中具体的例子来看一看这个过程,假设现在有三个网页A、B、C,之间的链接关系就是下面的图:
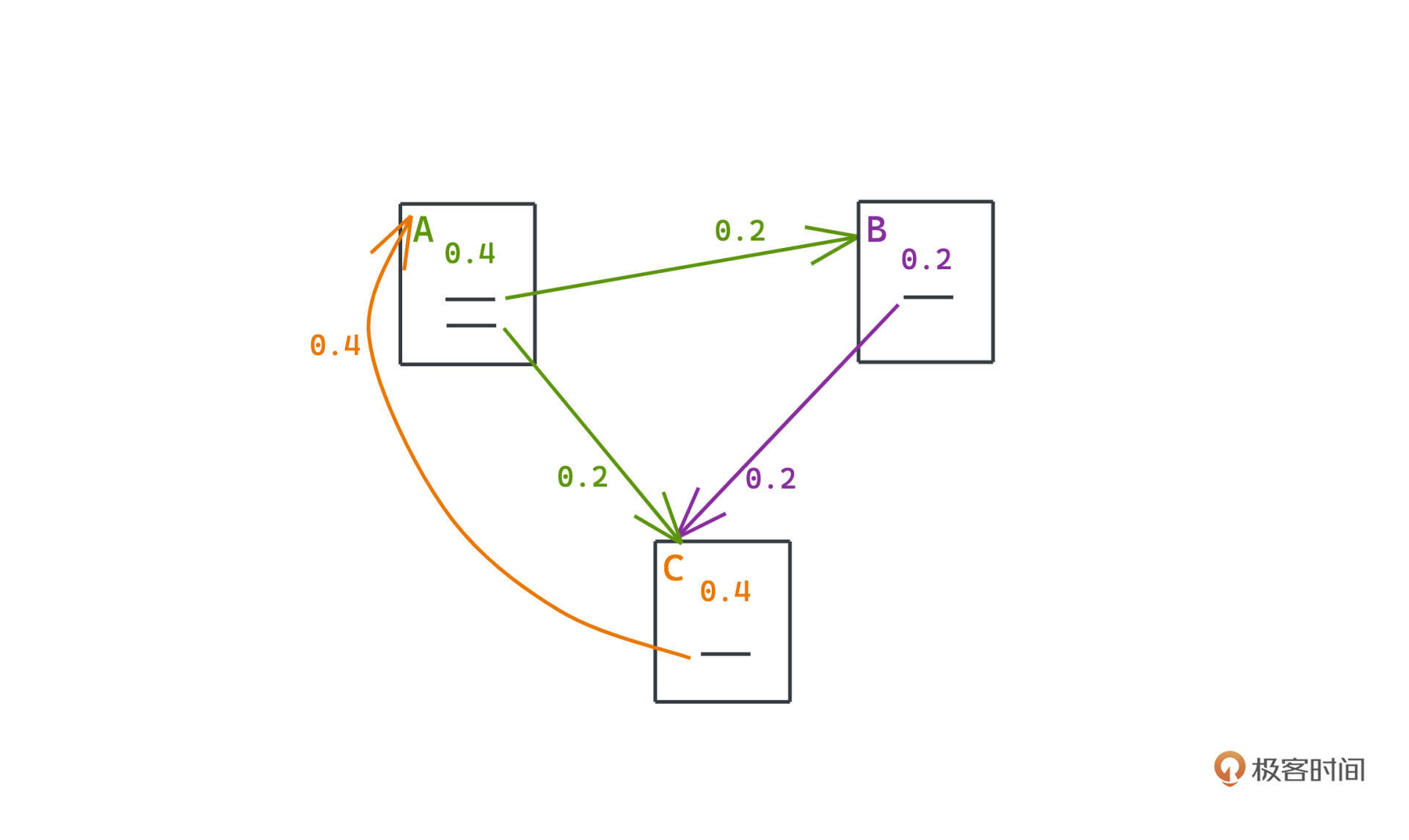
如果按照前面说的方式进行权重的转移,我们可以得到一个类似于马氏链的状态转移矩阵,矩阵的每一列都代表某个网页的权重如何传递到其他网页上(A的50%到B,50%到C;B的100%到C;C的100%到A):
$$
\left[\begin{array}{ccc}
0 & 0 & 1 \\\
0.5 & 0 & 0 \\\
0.5 & 1 & 0
\end{array}\right]
$$
所以如果用这个矩阵乘以表示每个页面权重的向量,得到的新的向量,自然代表一轮计算之后的网页权重。
假设我们初始化三个网页的权重都是 1/3 ,那么:
$$
\left[\begin{array}{ccc}
0 & 0 & 1 \\\
0.5 & 0 & 0 \\\
0.5 & 1 & 0
\end{array}\right] *\left[\begin{array}{c}
1 / 3 \\\
1 / 3 \\\
1 / 3
\end{array}\right]=\left[\begin{array}{c}
1 / 3 \\\
1 / 6 \\\
1 / 2
\end{array}\right]
$$
经过一次权重分配计算之后,得到的新的权重是 1/3、1/6、1/2。
我们继续反复进行这样的转移和分配,进行12次计算之后,得到的新的权重就是 (77/192 19/96 77/192) 写成小数是 (0.401 0.198 0.401),很容易发现,权重会渐渐收敛到 0.4 0.2 0.4。
这其实就是所谓的马氏平稳状态。如果你用 0.4 0.2 0.4 作为网页权重再做一次计算,会发现整个网页的权重不会再有任何变化。
$$
\left[\begin{array}{ccc}
0 & 0 & 1 \\\
0.5 & 0 & 0 \\\
0.5 & 1 & 0
\end{array}\right] *\left[\begin{array}{c}
0.4 \\\
0.2 \\\
0.4
\end{array}\right]=\left[\begin{array}{c}
0.4 \\\
0.2 \\\
0.4
\end{array}\right]
$$
总的来说,在这个简单例子里,无论如何初始化网页权重,在这样的链接情况下,所有网页的权重都是固定可以计算出来的。A和C的权重高一些也很容易理解,因为相比于B,有更多的链接指向A和C。
在更大的图上,这样的收敛性质,在所有节点强连通的情况下依然是可以得到保障的。所以在有限次的计算中,一旦给定了网页链接图,所有网页的权重都是收敛到一个稳定值的。那么在搜索的时候我们基于这个权重来做排名,就可以得到一个比较优的搜索结果了。
但是,在推导问题时我们用的例子是一种特殊的网络链接图,所有的节点都是既有出边也有入边的,对于真实的网页链接来说,考虑到边界情况,还有两个问题需要处理一下:
第一个就是Dangling links,指的是那些有入边但是没有出边的节点,在网页链接图中,有这样的节点存在会导致很大的问题。
我们仔细思考一下刚刚的计算过程,很容易发现,整个过程的所有页面权重之和是没有变化的,这是因为每个被转移到某个节点的权重,都会在下一轮计算中被平均地分配到其他页面上。
但是如果出现了Dangling links,情况会大有不同,所有分配到那些只有入边,但没有出边的节点上的权重,都不会再有机会转移到其他节点了。这些节点就像一个个黑洞,吸收着网页上所有的权重,随着不断迭代,整个图上的权重仍然会收敛,但是会全部收敛为0。这显然是不可接受的。
那要如何解决这个问题呢?Larry Page 认为,这样的节点对其他节点权重的计算没有任何贡献,既然让它们参与计算会导致所有权重收敛为0,不如直接把它们都移除。
不过这个移除过程可能会导致新的 Dangling links 产生,所以整个过程需要迭代地进行,直到剩余的网页中不再存在 Dangling links。当然,被移除的额外节点会对整个马氏链的计算产生一定影响,但是Larry Page 认为这个影响在谷歌搜索引擎收纳的巨量网页前是可以接受的。
移除后,等新的网页链接图上的计算收敛,我们再把被移除的节点加入图中,进行权重计算,但是不去修改所有已经收敛的权重,这样就可以得到全部网页的权重了。
第二个要处理的问题是 Spider Traps。这个问题和Dangling links的情况有点像,说的是图中另一种节点,虽然有出链,但是出链只指向自己。
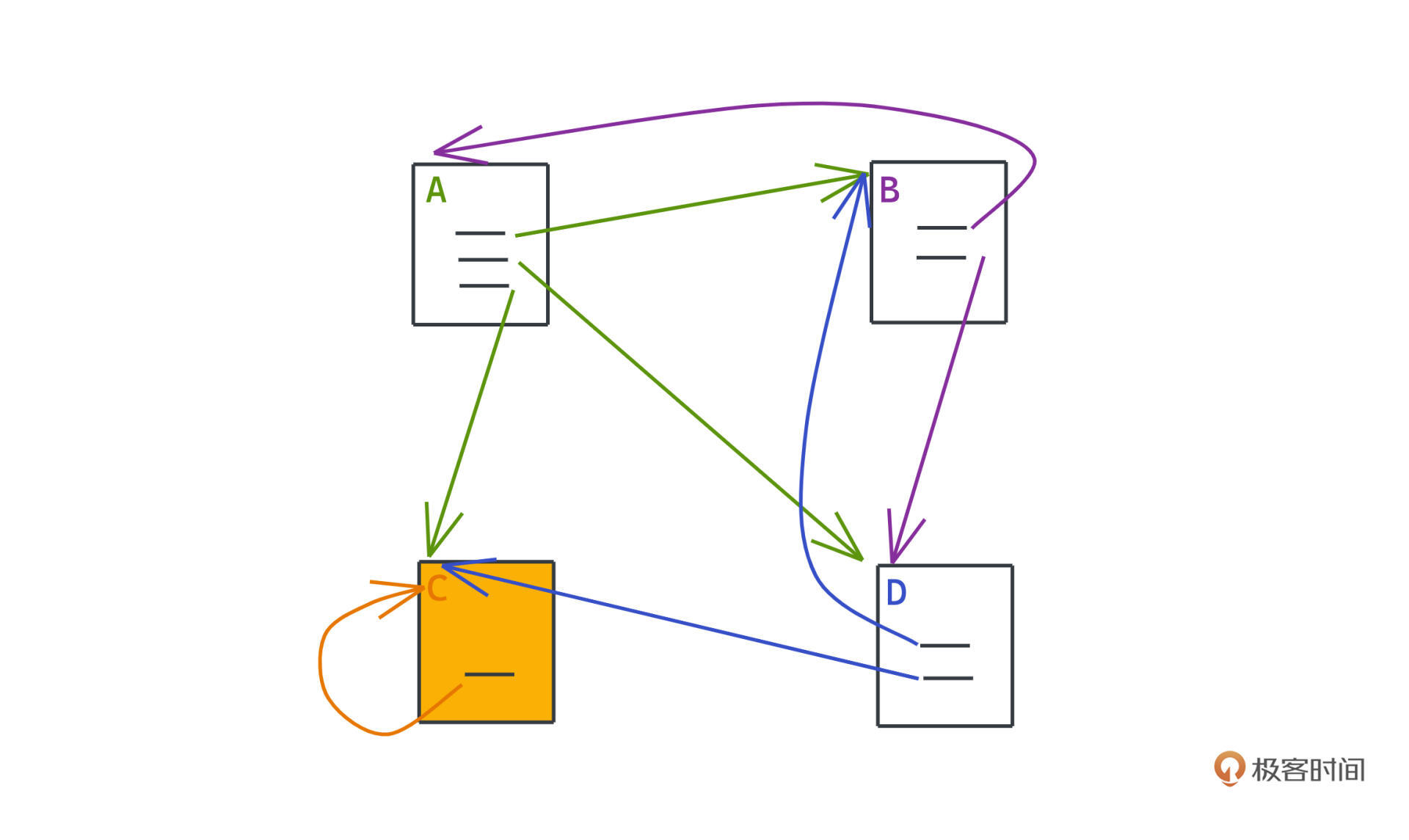
比如图中的C就是这样一个节点,感兴趣的话,你可以自己列一下转移矩阵,做一做权重的计算感受一下。如果图中存在这样的节点,运行PageRank算法之后,权重仍然会收敛,不过这次就是所有的权重都集中在C这一个节点上了。
不过即使没有这样的节点存在,因为网页数量众多,而链接相对有限,整个网页链接图是比较稀疏的。
可以想像运行PageRank之后,很可能节点之间的权重分布很不均匀,有一部分节点处于网络的边缘且入边很少,所以权重几乎为零,而另一部分权重会比较大。那我们怎样才能做到尽量地共同富裕,让权重结果更加均衡一些呢?
思路很简单,就是添加一个跳转因子$\beta$,让每个网页都雨露均沾,相当于增加到所有其他节点的一个链接,只不过权重很小。但是只要增加了,就足以让每个网页的权重不至于接近于零,可以平滑整个图上权重的计算。
新的计算公式是:$$R=(1-\beta)MR’+e*\beta/N$$
R是权重,M是转移矩阵,e是单位矩阵。添加了跳转因子$\beta$后,每个新的权重计算就不只依赖原图中的链接,还考虑了雨露均沾的跳转因子。这样,Spider Traps就会被抑制了,至少不会出现某些节点上几乎没有权重的情况,可以得到一个比较合理的网页排名权重。
好啦学习了这么多原理性的东西,现在你是不是迫不及待想要实现一下呢?
思路也很简单,无非就是建图,然后迭代地计算权重,重点就是判断一下收敛条件。
比如上一轮结果和这一轮结果的差距是否小于一个阈值,是的话,就停止计算;或者更简单直接规定一个迭代轮次,因为即使在很大的图上,估计也只需要百次左右的迭代,整个网络就会趋于收敛了。如果你是数据分析高手,可能直接用Python套个科学计算的库,利用矩阵计算,10几行代码就可以完成这项工作了。
嗯,听起来很完美是吧?但是不要忘了,我们面对的是海量的网站数据,单机的环境是远远搞不定的,这个时候就是我们上一节课学习的MapReduce的用武之地了。
不过MapReduce和Hadoop确实已经是上一代的大数据计算引擎了,我们这次就用Spark来实现一下(如果你对Spark不熟也没有关系,整个实现非常简单,相信你看代码也很容易理解)。主要是想说明一下MapReduce这样的计算框架的高度抽象和泛化能力,让它可以解决绝大部分分布式计算问题,而PageRank正是绝佳的使用场景。
废话不多说,我们直接写代码:
def main(args: Array[String]) {
if (args.length < 1) {
System.err.println("Usage: SparkPageRank <file> <iter>")
System.exit(1)
}
showWarning()
// spark 初始化
val spark = SparkSession
.builder
.appName("SparkPageRank")
.getOrCreate()
// 迭代轮次
val iters = if (args.length > 1) args(1).toInt else 10
val lines = spark.read.textFile(args(0)).rdd
// 转化为邻接表
val links = lines.map{ s =>
val parts = s.split("\\s+")
(parts(0), parts(1))
}.distinct().groupByKey().cache()
// 初始化所有节点的权重为1
var ranks = links.mapValues(v => 1.0)
for (i <- 1 to iters) {
// 将所有的处边对应的权重分配计算出来
val contribs = links
.join(ranks)
.values
.flatMap{ case (urls, rank) =>
val size = urls.size
urls.map(url => (url, rank / size))
}
// 进行累积求和
ranks = contribs.reduceByKey(_ + _).mapValues(0.15 + 0.85 * _)
}
val output = ranks.collect()
output.foreach(tup => println(tup._1 + " has rank: " + tup._2 + "."))
spark.stop()
}
假设我们输入的是网页之间的边表:
url_1 url_4
url_2 url_1
url_3 url_2
url_3 url_1
url_4 url_3
url_4 url_1
代码会先把边表转化为邻接表,相关的概念我们之前学搜索和网络的时候都有提过,你不熟悉的话可以看这里回顾。
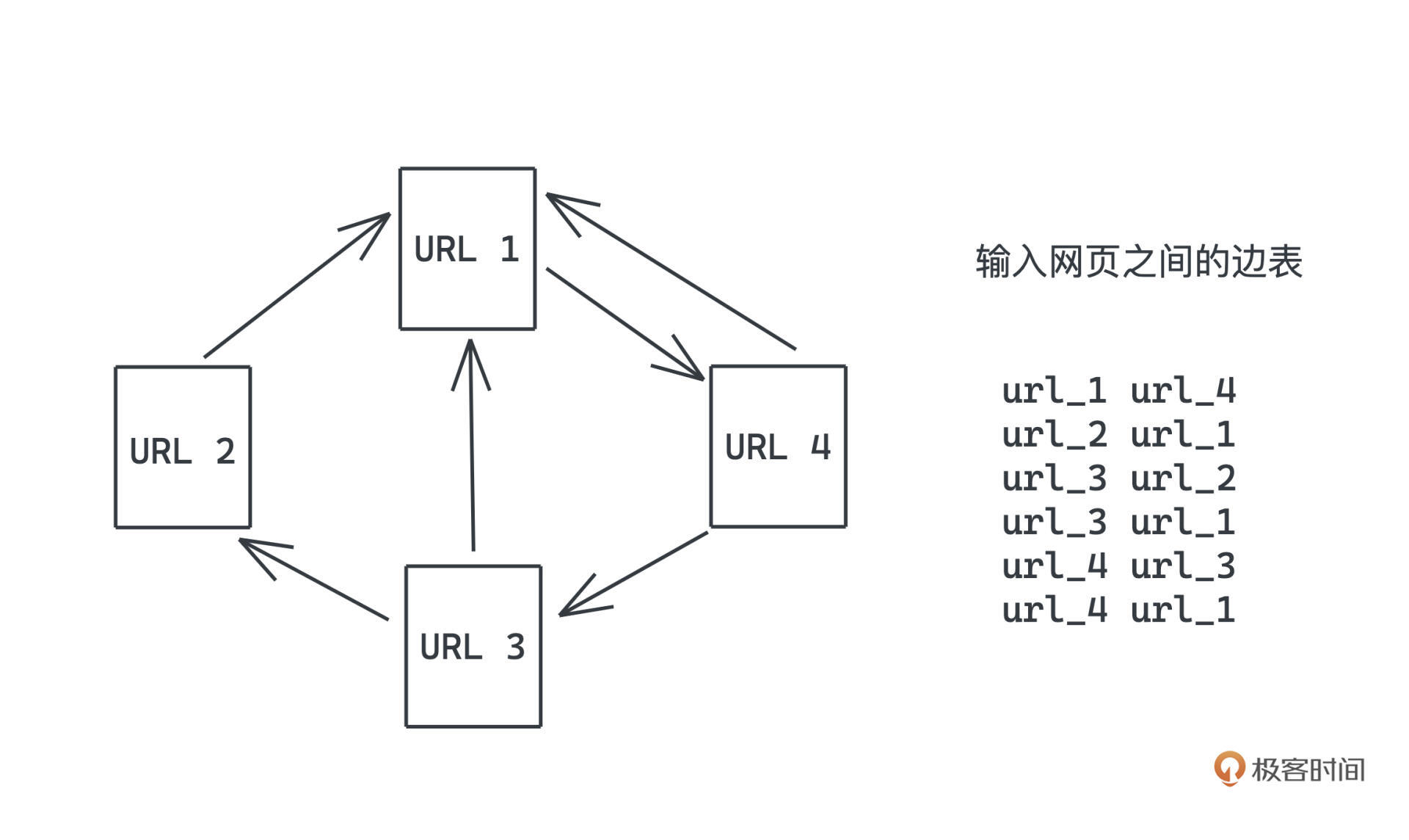
有了邻接表之后主要就是两步:
整个过程以及中间结果都是在Spark计算集群中分布式计算、分布式存储的。而且写出来的核心代码非常简洁,这就是MapReduce的威力了。
经过20轮的迭代,在上面的图中,我们可以得到这样的计算结果:
url_4 has rank: 1.3705281840649928.
url_2 has rank: 0.4613200524321036.
url_3 has rank: 0.7323900229505396.
url_1 has rank: 1.4357617405523626.
感兴趣你也可以自己部署一个单机版的Spark试一试。
今天我们学习了谷歌三驾马车之二 PageRank 算法,核心是利用网页之间的链接关系,通过迭代的方式计算网页的权重,帮助谷歌获得了更好的搜索质量,打败了竞争对手。
PageRank 的应用非常多,比如一个很常见的,它可以用来帮助微博挖掘平台上有影响力的大V。这些应用往往都需要大量的计算资源,MapReduce或者Spark这样的分布式计算平台,可以很好地帮助我们屏蔽底层的技术细节而将研发人员的精力都放在业务开发之上。
其中为了解决Spider Traps,增加跳转因子的思想也很常见。比如,各种广告系统或者推荐系统,在广告或者内容没有历史数据的时候,我们就会为这些内容提供一些试探流量。这背后的思想其实和跳转因子也是类似的。相信当类似业务需要出现时,现在你可以想到解决方案了。
最后也给你再留一个开放式思考题,这样的PageRank算法有什么可以进一步优化的地方吗?
很期待在评论区看到你的想法。如果觉得这篇文章对你有帮助的话,也欢迎转发给你的朋友一起学习。下节课见~