你好,我是微扰君。
上一节我们学习了数据库中非常常用的索引数据结构——B+树,在过去很多年里它都是数据库索引的首选实现方式,但是这种数据结构也并不是很完美。
因为,每次修改数据都很有可能破坏B+树的约束,我们需要对整棵树进行递归的合并、分裂等调整操作,而不同节点在磁盘上的位置很可能并不是连续的,这就导致我们需要不断地做随机写入的操作。
众所周知,随机写入的性能是比较差的。这个问题在写多读少的场景下会更加明显,而且现在很多非关系型数据库就是为了适用写多读少的场景而设计的,比如时序数据库常常面对的IOT也就是物联网场景,数据会大量的产生。所以,如果用B+树作为索引的实现方式,就会产生大量的随机读写,这会成为系统吞吐量的瓶颈。
但是考虑到非关系型数据库的检索,往往都是针对近期的数据进行的。不知道你会不会又一次想到Kafka的线性索引呢?不过很可惜,非关系型数据库的workload也不是完全append only的,我们仍然需要面对索引结构变动的需求。
那在写多读少的场景下,如何降低IO的开销呢?
LSM Tree(Log Structure Merge Tree)就是这样比B+树更适合写多读少场景的索引结构,也广泛应用在各大NoSQL中。比如基于LSM树实现底层索引结构的RocksDB,就是Facebook用Golang对LevelDB的实现,RocksDB本身是一个KV存储引擎,现在被很多分布式数据库拿来做单机存储引擎,其中LSM树对性能的贡献功不可没。
那LSM Tree的秘密到底是什么呢?
其实说起来也不复杂,还记得我们当时讲UUID的时候提到过的“批量生成”策略吗,很多时候,如果批量地去做一些事情,就能获得更好的效率。
在读写磁盘的场景中也是一样,既然B+树的多次随机写入性能不佳,我们有没有办法把多次写入合并成一次写入,从而减少磁盘寻道的开销呢?LSM Tree正是这样做的。
早期,LSM Tree中包含了多个树状结构,C0-tree存储在内存,而C1-tree存储在磁盘中,实质就是利用内存,延迟写入磁盘的时机。

C0-tree 由于常驻内存,检索起来不会产生IO,所以理论上,我们可以使用各种可用于高效索引的数据结构来存储数据,比如红黑树、跳表等等。但是因为内存成本高昂,能存储的数据必然有限,更大量的数据仍然需要存储在磁盘里。而磁盘中的C1-tree一般被实现为特殊的B+树。
数据的存储也会分为两个阶段,我们会一直先在内存中存储元素,直到内存中的数据到达一个阈值,我们会开始和C1-tree中的节点进行合并和覆写,过程和多路归并有点相似。因为我们可以决定写入磁盘的时机,所以完全可以保证B+树的所有节点是满的,也就避免了许多单次的随机写操作。
实现细节我们不用掌握,只需要明白设计实质就可以了,感兴趣的话你可以翻阅最早的LSM tree的论文了解。
现代的LSM-tree已经抛弃了这样繁琐的结构,但核心仍然是一致的,都是通过内存维护有序的结构,延迟写入磁盘的时机,通过合并多次随机写操作,降低磁盘臂移动的开销,在多写少读的场景下能获得比B+树好许多的性能。
整个LSM树包含了三个部分,memtable、immutable memtable、SSTable,前两个在内存中,最后一个在磁盘中。同样,我们会先临时地把数据写在memtable中,然后在合适的时机刷入磁盘上的SSTable中。
看到这里,不知道你会不会有一个疑问,这个过程听起来好像很不靠谱呀?众所周知,内存是非持久化的存储介质,如果写入内容写到一半的时候断电了,考虑到延迟刷盘的机制,岂不是之前的数据都丢失了,而且很多可能是我们已经认为提交了的修改记录?
如果你还记得我们之前在操作系统篇学习的WAL机制,就能想到这个问题的解决方式了吧?没错,在LSM-Tree中我们正是通过预写日志的方式,来保证数据的安全性。
每次提交记录的时候,都会先把操作同步到磁盘上的WAL中做备份,如果断电,我们也可以从WAL中恢复所有的修改记录。而且WAL是典型的Append Only的日志存储格式,并不是随机读写,虽然引入了额外成本,但是能明显避免许多随机写的操作,还是能带来巨大的性能提升。
好解决这个困惑,我们来看LSM tree的三大组成部分,搞清楚它们是如何工作的。
Memtable显然是内存中的数据结构,存储的是近期更新的记录值,类似原始的LSM tree,可以用各种有序高效的数据结构来实现,比如HBase中采用的跳跃表,我们之后讲Redis的时候也会着重介绍这一数据结构,当然用之前介绍的红黑树也是可以的。
所谓近期的更新的记录值呢,在KV存储的场景下,就是你最近提交的对某个key的插入或者更新的记录,你可以简单的理解成一个Map中的key,value对就可以了。
在Memtable存储的元素到达一个数量级之后,我们就会把它固化成immutable table,从字面上理解,就是不可变表。
很明显这就是memtable的拷贝操作,那我们为什么要引入这样一个memtable的不可变副本呢?虽然现在还没学习具体的落盘过程,但是我们可以先猜测一下,拷贝过程是需要时间的,但同时我们的系统很可能仍然在对外工作,所以创建副本,可以很好的地帮助我们避免读写冲突竞争,从而避免阻塞,提高系统性能。
现在,我们拥有的是内存中的有序结构,存储了近期的记录变更,如何把这样的数据存储在磁盘上,既利用磁盘顺序读写的优势,也能保证所写的格式便于改动也便于查询呢?
SSTable就是一种很巧妙的设计,它是整个LSM Tree的核心,毕竟我们的大部分数据都是存储在磁盘上的,SSTable就是在磁盘上做持久化的部分。本质其实很简单,就是一段段按照key有序排列的键值对(最早出自Google的bigtable论文,后来在工程实践中加了很多优化):
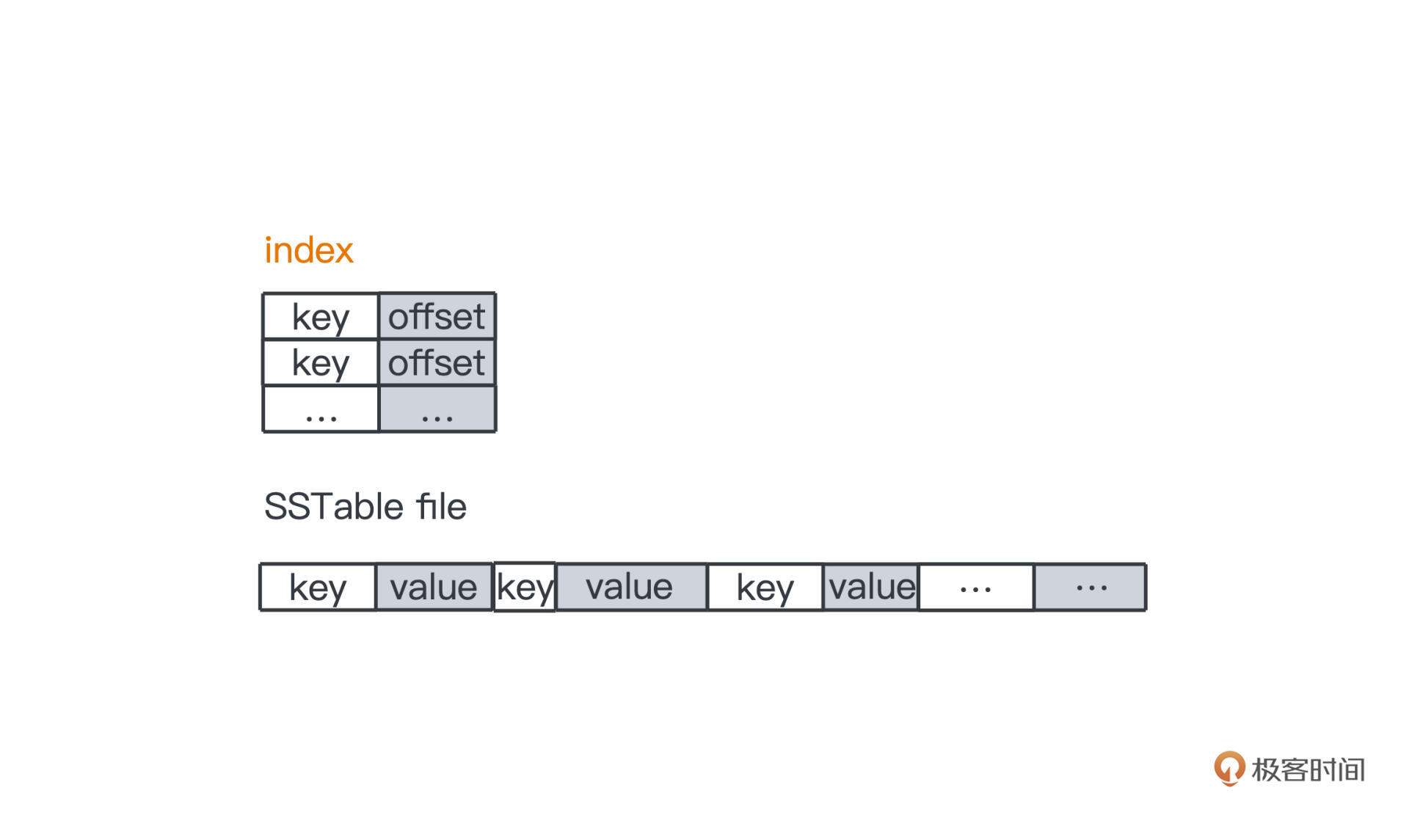
原始的SSTable,key和value可以是任意大小的,所以直接在磁盘上查询不是特别靠谱,但是SSTable本身的有序性,让我们可以采用类似Kafka的线性索引来加速查询过程,所以SSTable一般也会带上一个索引文件,值存储的是key所对应的offset,加载到内存后,我们利用二分搜索可以很快查找出要访问的key的值。
好,我们知道内存中的数据一定是有序的,而持久化数据到磁盘最高效的方式就是顺序写一遍,每次内存中的数据,我们都一次性dump成磁盘上的一段自然是比较快的,这样一段段的数据,我们就称为一个个segment。所以最简单的持久化方式就是我们在磁盘上把内存中有序的键值对直接dump成一个个段,也就是segment。
当然,后面存储的段和前面存储的段,key可能是重复的,因为后面的段新一些,所以在有重复的时候,最靠后的段中的记录值,就是某个key最新的状态。
整个持久化的过程就像这样,我们把内存中有序的数据结构比如红黑树中的记录,dump到一段磁盘上的空间,然后按segment一段一段往后叠加。
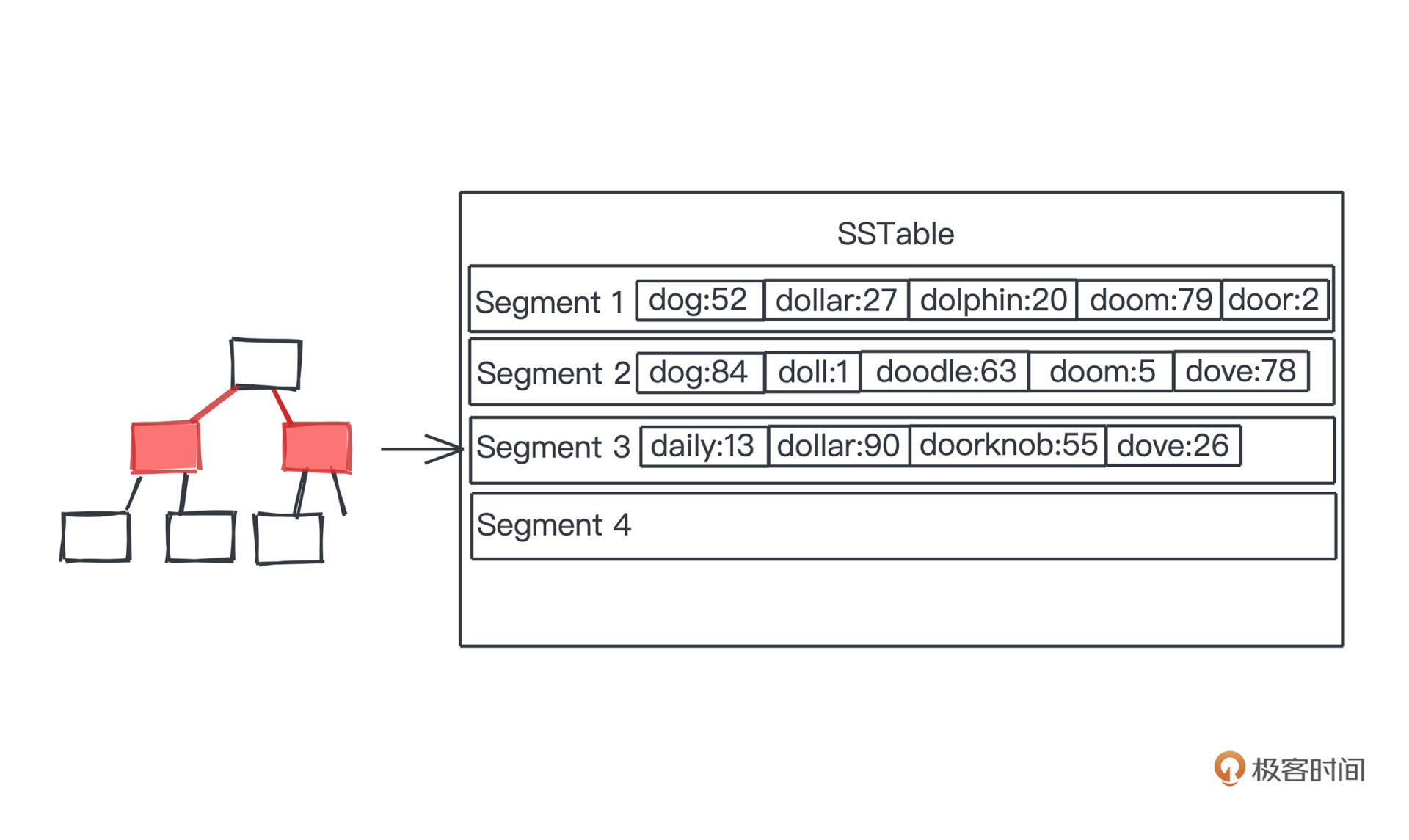
那在这样的存储下,检索数据的时候需要怎么做呢?很简单,就是从后面的段开始,往前遍历,看看是否有查找到目标key,有的话就返回。由于从后往前遍历,我们第一次查询到key的时候,一定就是这个key对应的最新状态。
但很显然,这样的存储会有很多问题。
总而言之,虽然说在写多读少的情况下,我们可以稍微降低一些读的速度,来换取更快的写的速度,但是这样无止尽的读性能劣化显然是不可接受的。怎么解决呢?
我们需要合并segment。
每个segment都是有序的,那我们显然可以比较高效地对多段数据进行合并操作,之前讲外排的时候也有提到,就是“多路归并”的思路,一般,多路归并的程序我们会在后台不断运行,我们会不断地把多个老的segment合并成一个更长的、同样有序的segment。
合并前老的segment长度都是一样的,在SSTable的主流实现里,我们会把不同的阶段被合并的segment放到不同的层中,并限制每一层数量,当某层segment超过一定数量,我们就会把它们删除,合并出一个更大的segment放入下一层。
低层中的segment显然是更新的记录值,更高层的则是更老的记录值。
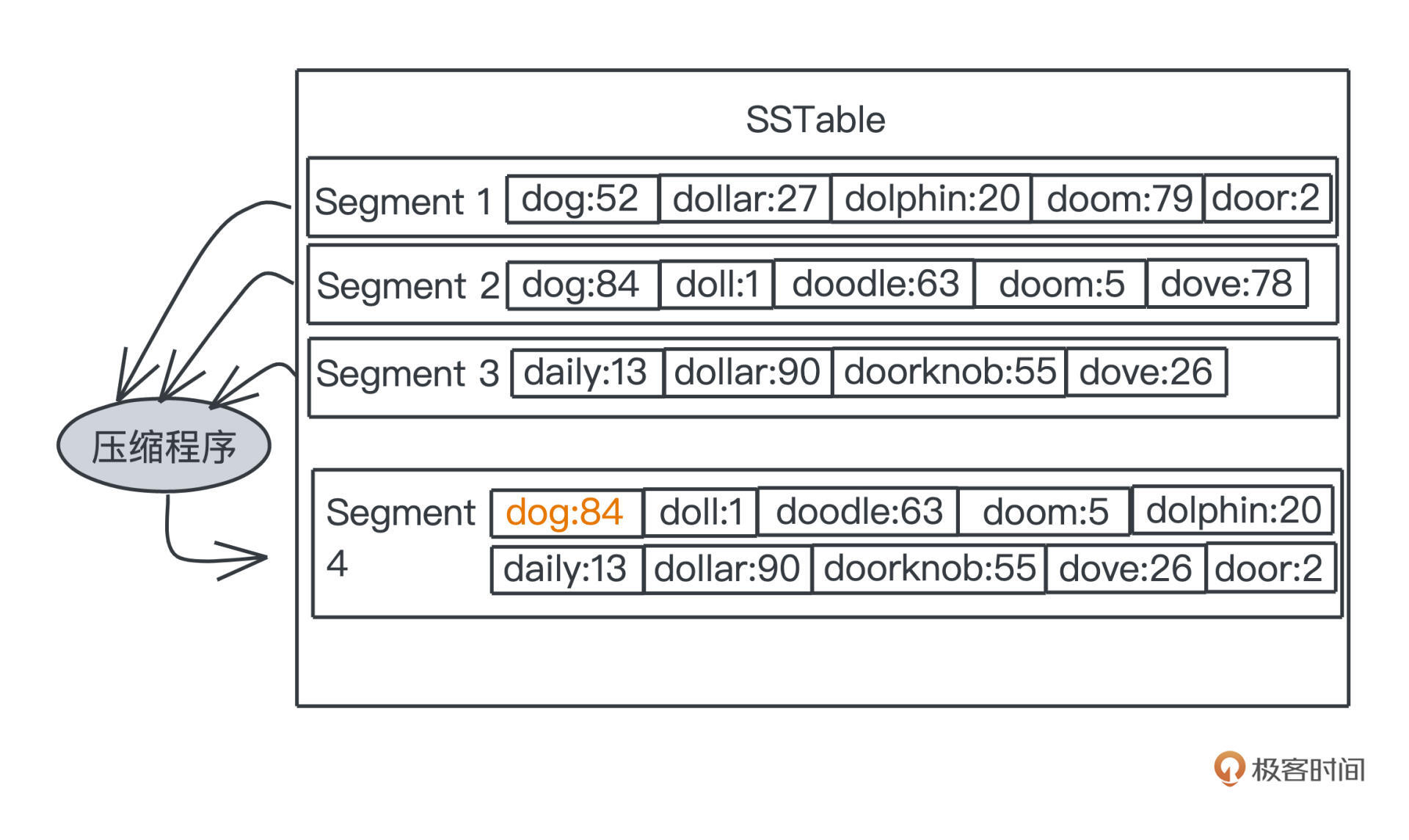
在图的例子中可以看出来,我们合并segment1、2、3之后,在得到的segment4里,dog的记录就只剩更新的segment2中的记录84了。这样我们的整个存储空间就不会无尽地膨胀,最高的一层,最多也就是占用历史以来所有出现过的key和对应的记录值这样数量级的空间,而存储这些是数据库本应做到的。
检索的时候,我们只需要按照“内存->level0->level1”这样的顺序,去遍历每层中不同段是否包含目标key。每个段内都是有序存储的,所以整体读的时间复杂度也是可以接受的,
确实可能会比B+树的查询效率低一些,不过辅以布隆过滤器等手段,劣化也不会非常明显,在许多读写比不到1:10的场景下,顺序写带来的写性能提升是非常令人满意的。
我们了解了如何存储数据、如何检索数据,那如何删除数据呢?
和B+树直接在本地进行删除的策略不同,LevelDB其实不会真的把某个数据移除,因为一旦移除,就可能需要去不同的层进行数据的清理,代价比较高昂。
一个聪明的做法就是我们用和写入一样的手段,将数据标记成一种特殊的状态。这种通过标记而不是真实移除数据的方法,在业务开发中其实也很常见,有时候我们称为soft delete。在有些ORM库中会直接通过deleteAt字段,标记删除时间,来表示这个数据被删除了,想恢复这个数据的时候也很简单,直接将deleteAt置空即可。
在LSM tree中也是一样,我们把这个特殊的状态称为tombstone,墓碑,看图就非常清楚了。
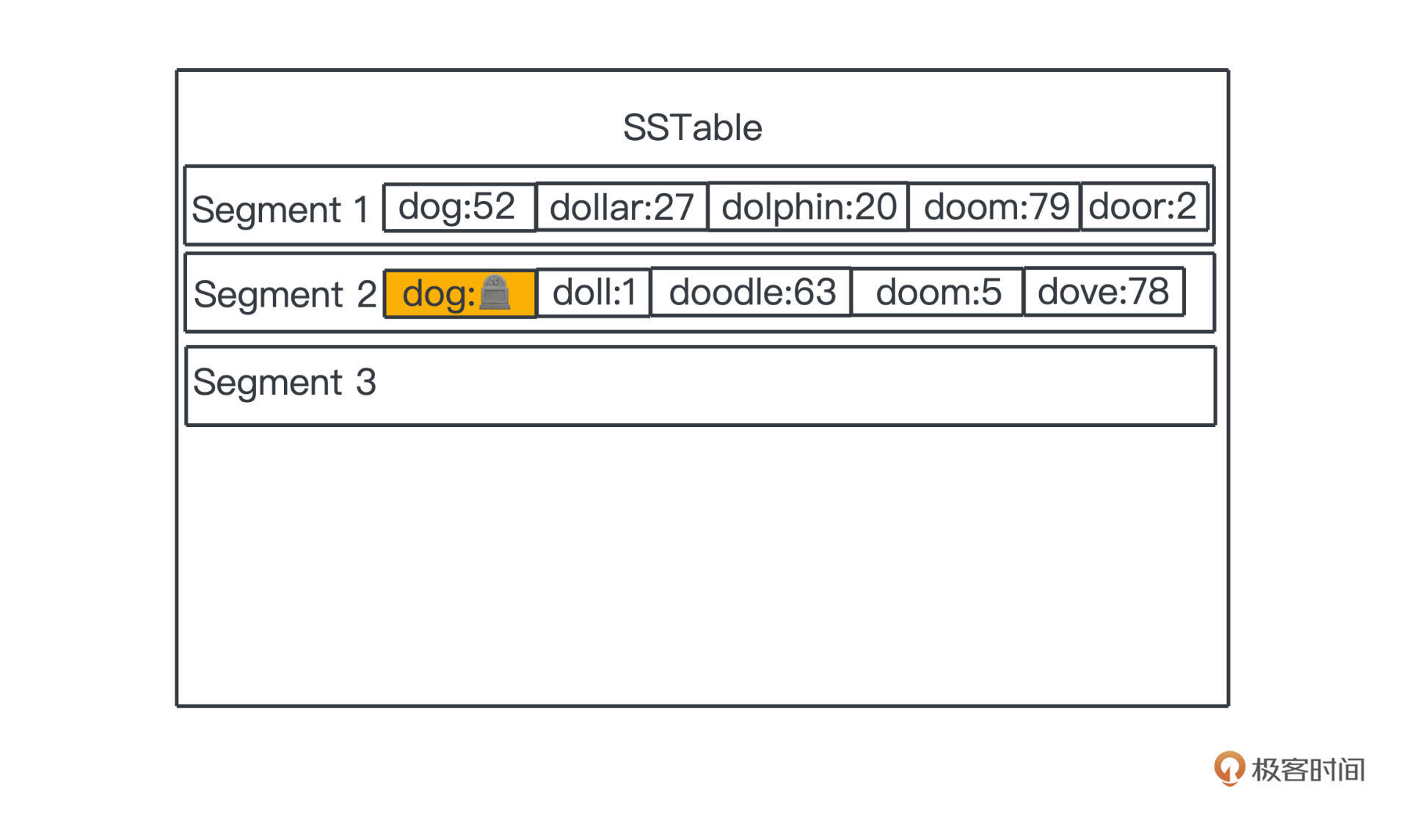
查询的时候,如果我们先查到了tombstone,就可以认为数据已经不复存在了。
今天我们学习了一个相对简化的modern LSM tree的实现,分为内存和磁盘上的数据结构两部分:
为了提高查询效率,我们引入了稀疏索引和布隆过滤器。其中稀疏线性索引,在Kafka的章节我们已经学习了,布隆过滤器很快也会介绍,核心就是可以帮助我们快速过滤掉一些肯定在数据库中不存在的字段。
整个LSM Tree的实现还是比较复杂的,重点体会批量写对性能的提高,在你的工作中有一天也许会做出类似的优化。
另外相信你也能感受到,从本篇开始常常提到之前学过的一些思想和算法,这也是这些大型系统之所以难以掌握的原因之一,涉及很多基础算法知识。不过当你能把它们串联起来灵活运用,也就不会觉得特别难啦;相信这些思想对你工作中的系统设计也会有很大的帮助。
前面说segment都是一段段的,如果让你来实现一个基于LSM索引结构的数据库,最小的segment应该设置成多大呢?
欢迎你在留言区留下你的思考,觉得这篇文章对你有帮助的话,也欢迎你转发给你的朋友一起学习。我们下节课见。