你好,我是微扰君。
上一讲我们学习了如何基于bitmap,使用少量内存,对大量密集数据高效地去重和排序,本质就是通过一个长长的二进制01序列,来维护每个元素是否出现过这样的二值状态,这个数据结构非常重要,日常工作中有很多应用,比如我们今天要学习的布隆过滤器,就建立在相似的数据结构之上。
那什么是布隆过滤器,用来解决什么样的问题呢?我们先从缓存说起。
还记得之前介绍LRU的时候,我们提过的缓存思想吗,用一些访问成本更低的存储,来存一些更加高频的访问数据,提高系统整体的访问速度。比如在业务开发中,我们经常会用Redis来缓存数据。
这就是因为Redis主要把数据存储在内存中,访问速度比数据库快得多,引入缓存层之后,能大大减少数据访问的延时,也能降低数据库系统本身的压力。
我们的用法通常是这样:每次请求某个数据的时候,假设都是基于某个key去访问数据库,比如用户ID之类的字段,我们会先试图访问Redis,查看是否有key相关的缓存记录,有的话就可以直接返回了;如果没有,再去数据库里查询,查到结果后会把数据缓存在Redis中;如果数据库中也没有,返回没有相关记录,这样Redis中自然也不会有缓存数据。
另外,大部分系统访问数据的时候都会有时空局部性,也就是说最近访问过的记录很有可能会被再次访问到,所以加了Redis之后,数据库的压力就会小很多。当然,这里我们需要处理缓存数据过期或者缓存和数据库数据不一致之类的问题。
所以总的来说,如果我们想要通过Redis避免数据库的压力太大,就得保证查询的数据很大一部分是在Redis中有缓存的。
大部分场景下,由于时空局部性,都是可以满足这个条件的,但是如果有人恶意反复去系统访问那些已知不存在的key呢?
由于数据库中一定不会存在这样的key,Redis中也不可能有这样的key,我们的每次请求都会访问一次Redis再访问一次数据库,就好像穿透了Redis层一样,这个问题我们就称为“缓存穿透”,恶意攻击者往往可以通过这样的手段,让我们的数据库的压力很大,甚至崩溃。
但是即使在正常的workload下,有时候也会产生大量穿透的请求,有什么办法减少这些不必要的请求呢?
布隆过滤器,也就是 bloom filter,可以很好地帮助我们解决这个问题。
顾名思义,布隆过滤器起到的是过滤的作用,在缓存穿透的场景下,过滤掉肯定不在系统中key的相关请求。所以,布隆过滤器,核心就是要维护一个数据结构,我们通过它来快速判断某个key是否存在于某个集合中。
看到这里,你是不是马上想到了一种最简单的filter策略:既然Redis做的就是一个缓存系统,如果存在key,我们把数据缓存至Redis中,不存在key的时候,我们一样缓存到系统中,然后记录一个特殊的值来表示这个数据不存在,这样不就可以了嘛,就像我们之前学的LSM-tree中的墓碑标记一样。
这个方案当然是可以工作的,但是,不存在的key,显然取值范围是很大的,我们也可以预想在大部分场景下,要比存在于系统中的key的取值范围多得多。Redis存储空间有限,所以,这个方案无疑会大大减少有效数据的缓存空间。在恶意攻击者的攻击下,甚至可能造成Redis中存储的大部分数据都是标记为不存在的记录,所以这显然不是一个很好的办法。
我们有没有办法利用更少的空间,快速判断某些记录是否存在于系统中呢?
这就是布隆过滤器的主要优势了,当然,软件没有银弹,布隆过滤器也有两个比较大的限制:
为什么会这样呢,接下来我们就来看一看布隆过滤器的实现原理。
布隆过滤器本质上可以理解成一种散列的算法,这也是为什么我们说它和上一讲学到的Bitmap关系很大。
不过布隆过滤器不是一个简单的映射,更像是一个散射,它包含K个不同的散列函数,每个散列函数都会把某个key映射到一个数字h,然后我们会把一个M位二进制对应的第h位二进制,置为1。这样,每个key,我们就映射到m位二进制中k位为1的数字上了,记录的方式其实和bitmap的定义如出一辙。
在整个布隆过滤器的使用过程中,我们会维护一个全局的Bitmap,并且把每个出现过的记录值都进行这样的散射,Bitmap的每个散射到的位置都置为1。
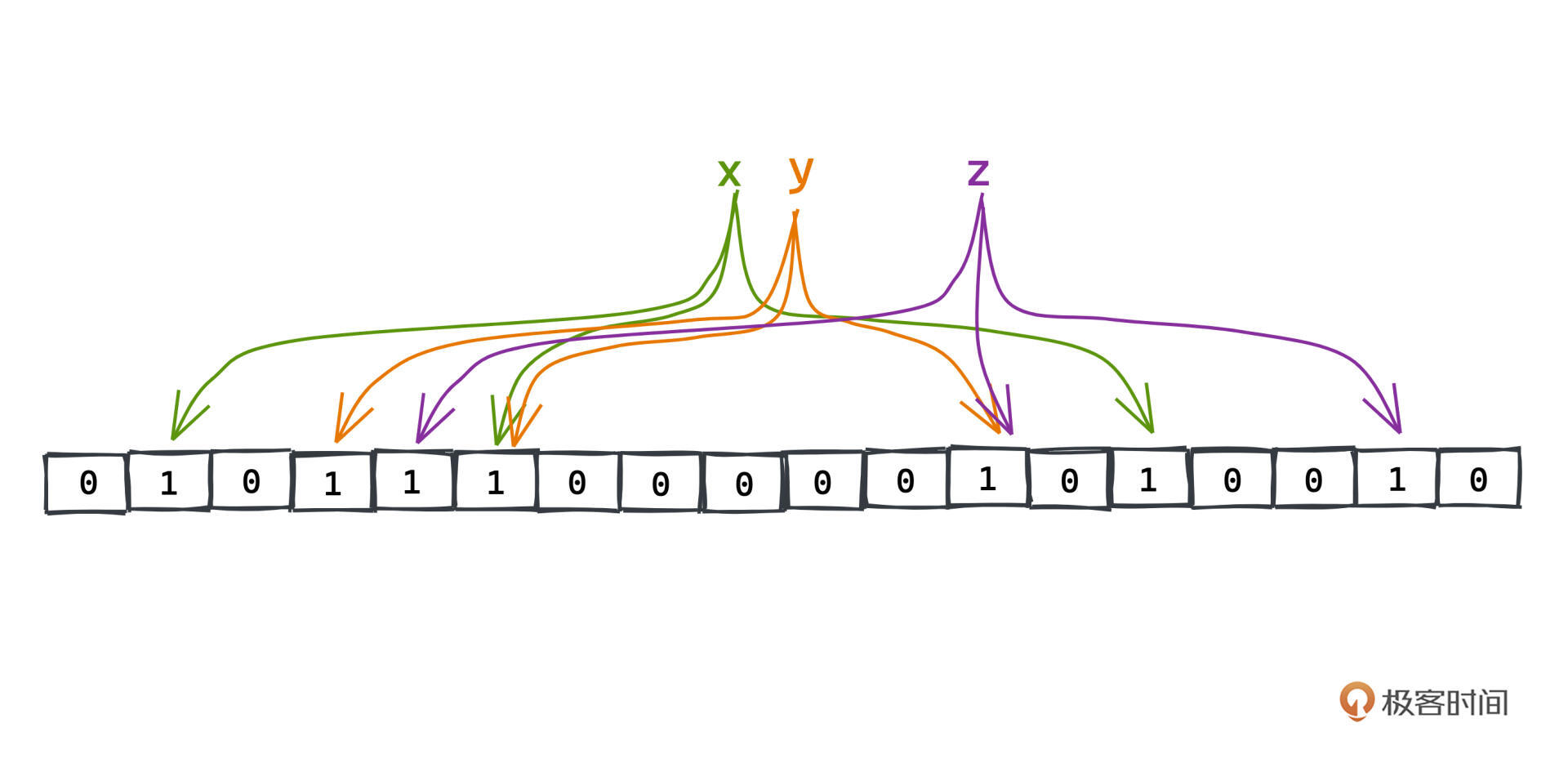
看这个例子,我们把x、y、z分别散射到了绿色、橙色、紫色指针的位置:

之后再查询不同的key,比如x、y、z,我们首先会进行同样的Hash计算,判断出每个对应的位置是否为1,如果有一位不为1,说明这个key肯定在系统中不存在,我们也就不需要进行后续的查询了。这样我们能减少很大一部分缓存穿透的情况,而且付出的存储空间也非常有限。
这样多重Hash方式有什么好处呢?
比如之前提到的直接用HashMap的实现方式,因为我们完全可以直接对xyz进行某种hash算法,将它们映射到一个数组空间里,再判断对应的key是否存在呀?多重Hash有什么优势呢?
主要的问题是HashMap所占用的存储空间要高得多,在传统的HashMap中,我们会存储key的引用,这是一个很大的开销。而在布隆过滤器中,我们所需要的只是一个不大的Bitmap(至于到底选择多大的bitmap合适,我们稍后具体的计算)。
当然,我们去掉了引用所占用的空间,自然也就少了应对冲突的能力,这就是布隆过滤器不完美的地方之一,它的重复判断是有“误差的”。
根据前面的原理,我们来详细分析一下,只要确定布隆过滤器中不存在的key,则该key在系统中一定是不存在的,因为但凡有一个Hash值对应的Bitmap位不为1,说明这个key一定没有被添加到过bloom filter中。
但是反过来,如果每一位都为1,其实仍然有一定的概率这个key没有出现在布隆过滤器中。比如例子中的w:
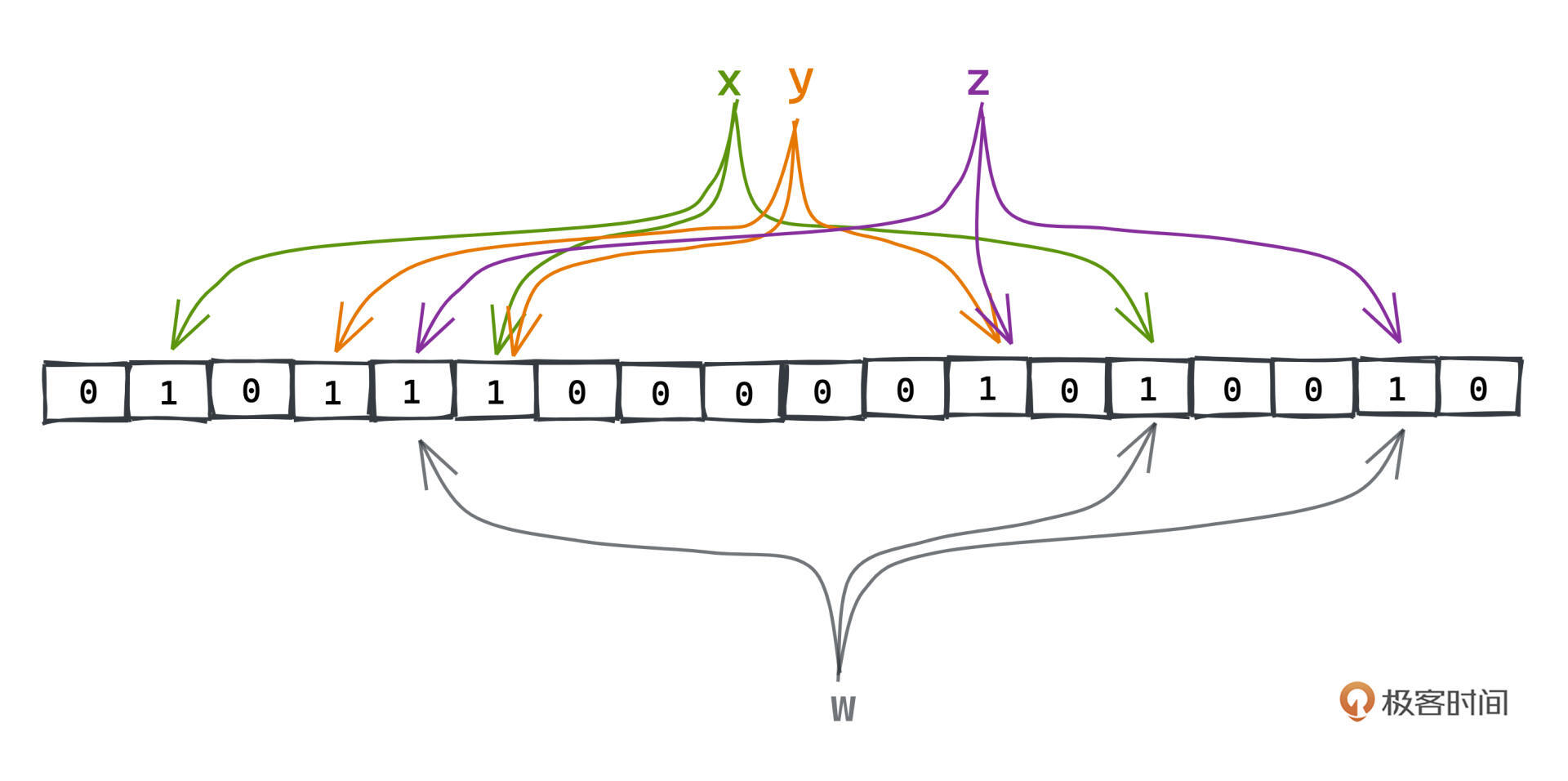
w映射的每个Bitmap的位正好都是x、y、z中某个key映射的一位,从布隆过滤器中看来,w的每一位也都是1,我们并不能排除它在系统中存在的可能性,但是如果w不存在,就会产生一次不必要的穿透。
但是缓存系统是空间敏感的应用,这也是我们没有直接用Redis存储不存在记录的原因,为了使用更小的空间,付出小概率的“误差”成本完全是可接受的。
第二个劣势记录删除困难,根本原因和上一点是一致的,因为我们重叠了Hash的位数,所以无法判断每一位的1到底是由哪一次Hash计算贡献的,同一个1可能被多次Hash计算更新,所以我们不好在想要移除某个字段的时候,把通过Hash计算得到的位直接置0。不过这个问题在许多需要使用布隆过滤器的场景下影响也不大。
好现在明白了布隆过滤器的设计思路与优劣势,工作应用时到底选择多大的bitmap合适呢,我们来根据误判概率算一算。
假设Bitmap由m位二进制组成,包含k个哈希函数。判断某个key是否存在的概率怎么算呢?
首先,判断是否存在,就是看这个key对应的k个位置是否都为1,那每个位置是否为1的概率从何而得呢?假设之前已经插入了n个key。
先考虑每次插入key的时候某一位为1的概率。如果哈希函数均匀,每个key一共进行k次哈希,每次哈希到特定某一位的概率为$\frac{1}{m}$,那么这一位不为1的概率是:$(1-\frac{1}{m})^{k}$。
再考虑这样的操作之前已经进行过n次,那么这一位不为1的概率是:$(1-\frac{1}{m})^{k*n}$。
最后反推,这一位为1的概率是:$1-(1-\frac{1}{m})^{k*n}$。
所以什么时候会误判呢?也就是说对于某个新的key,虽然这个key不存在,但是它k次Hash出来的每个位置都为1。这个概率的计算,我们随便找k个1,然后对每一位都为1的概率做累积,在m比较大的时候,通过高等数学的知识可以得到近似:
$$ (1-(1-\frac{1}{m})^{k*n})^{k} ={(1-e^{-\frac{kn}{m}})}^{k} $$
可以看出,误判概率大致和n成正比,和k、m成反比,我们可以根据自己的业务场景选择合适的位数和哈希函数数量。不同的m、n、k取值下,可以参考误判率的表格。
经验值是对于100w的数据量,如果希望通过5次Hash得到5%以内的误判率,我们大概需要700万位Bitmap,内存只需要不到1M即可完成,效果非常不错。而且5%的误判率,我们也是完全可以接受的,以数据库-缓存构成的系统为例,这足以帮我们降低95%的穿透请求,效果显著。
在理解布隆过滤器实现原理的基础上,我们动手实现就非常简单了,比Bitmap的实现多不了几行代码。
Google提供的经典Java工具库Guava中,就有一个对 bloom filter 的实现,它提供了很好的泛化能力,通过自己重新封装bitset获得了更佳的性能,同时也支持多种不同的策略。我们来看一下核心的逻辑:
MURMUR128_MITZ_64() {
@Override
public <T> boolean put(
T object, Funnel<? super T> funnel, int numHashFunctions, BitArray bits) {
long bitSize = bits.bitSize();
// 获得带有随机性的hash种子
byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
long hash1 = lowerEight(bytes);
long hash2 = upperEight(bytes);
boolean bitsChanged = false;
long combinedHash = hash1;
// 进行k次hash计算
for (int i = 0; i < numHashFunctions; i++) {
// Make the combined hash positive and indexable
bitsChanged |= bits.set((combinedHash & Long.MAX_VALUE) % bitSize);
combinedHash += hash2;
}
return bitsChanged;
}
@Override
public <T> boolean mightContain(
T object, Funnel<? super T> funnel, int numHashFunctions, BitArray bits) {
long bitSize = bits.bitSize();
byte[] bytes = Hashing.murmur3_128().hashObject(object, funnel).getBytesInternal();
long hash1 = lowerEight(bytes);
long hash2 = upperEight(bytes);
long combinedHash = hash1;
for (int i = 0; i < numHashFunctions; i++) {
// Make the combined hash positive and indexable
if (!bits.get((combinedHash & Long.MAX_VALUE) % bitSize)) {
return false;
}
combinedHash += hash2;
}
return true;
}
}
MURMUR128_MITZ_64 是其中一种比较常见的策略,核心方法就是put和mightContain方法。
从mightContain方法名中,相信你也可以再一次意识到bloom filter误判的特性,可以说Google的库命名非常确切。
put方法,核心逻辑就是通过murmur3_128进行Hash计算,得到一个128位带有随机性的byte,取其中的高位和低位作为种子,再通过简单的位运算叠加k次,等同了Hash k次的效果,最后把对应的位置都置1即可。mightContain的逻辑,基本上就是相反的过程。
Guava库的代码质量很高,也不是特别难懂,如果你是Java爱好者,不妨用这个库开始你的源码学习之旅。
今天我们一起学习了非常知名且常用的数据结构,bloom filter。在Bitmap和HashMap的基础上,布隆过滤器,通过对每个元素进行某种散射式的Hash,把状态记录在Bitmap中,高效且成本低地为我们提供了在大量数据中判断某个元素是否存在的神奇能力。
当然,相比于朴素的HashMap,省来的空间也不是完全没有代价,在布隆过滤器中,我们只能断言一个元素一定不存在,但没有断言时,元素可能存在也可能不存在。
不过在选取合适的Bitmap数组大小和Hash计算次数之后,可以很容易地把误判率控制在低于5%的水平,依旧可以给我们带来很大的性能提升。在Redis中,就常常用来缓解缓存穿透的现象,从而提高系统的吞吐和稳定性。
留一个有点难度的思考题。我们提到了布隆过滤器清除状态比较困难,但有些缓存数据是有生命周期的,比如一周或者一个月之后就大概率过期了,你有没有什么好办法可以帮助我们更好地清理过期数据呢?
欢迎你在留言区留下你的思考。如果觉得这篇文章对你有帮助的话,也欢迎你转发给你的小伙伴一起学习。我们下节课见~