前两节课结束后,我们已经掌握了表达式的解析,并通过一个简单的解释器实现了公式的计算。但这个解释器还是比较简单的,看上去还不大像一门语言。那么如何让它支持更多的功能,更像一门脚本语言呢?本节课,我会带你寻找答案。
我将继续带你实现一些功能,比如:
实现这些功能之后,我们的成果会更像一个脚本解释器。而且在这个过程中,我还会带你巩固语法分析中的递归下降算法,和你一起讨论“回溯”这个特征,让你对递归下降算法的特征理解得更加全面。
不过,为了实现这些新的语法,我们首先要把它们用语法规则描述出来。
首先,一门脚本语言是要支持语句的,比如变量声明语句、赋值语句等等。单独一个表达式,也可以视为语句,叫做“表达式语句”。你在终端里输入2+3;,就能回显出5来,这就是表达式作为一个语句在执行。按照我们的语法,无非是在表达式后面多了个分号而已。C语言和Java都会采用分号作为语句结尾的标识,我们也可以这样写。
我们用扩展巴科斯范式(EBNF)写出下面的语法规则:
programm: statement+;
statement
: intDeclaration
| expressionStatement
| assignmentStatement
;
变量声明语句以int开头,后面跟标识符,然后有可选的初始化部分,也就是一个等号和一个表达式,最后再加分号:
intDeclaration : 'int' Id ( '=' additiveExpression)? ';';
表达式语句目前只支持加法表达式,未来可以加其他的表达式,比如条件表达式,它后面同样加分号:
expressionStatement : additiveExpression ';';
赋值语句是标识符后面跟着等号和一个表达式,再加分号:
assignmentStatement : Identifier '=' additiveExpression ';';
为了在表达式中可以使用变量,我们还需要把primaryExpression改写,除了包含整型字面量以外,还要包含标识符和用括号括起来的表达式:
primaryExpression : Identifier| IntLiteral | '(' additiveExpression ')';
这样,我们就把想实现的语法特性,都用语法规则表达出来了。接下来,我们就一步一步实现这些特性。
之前实现的公式计算器只支持了数字字面量的运算,如果能在表达式中用上变量,会更有用,比如能够执行下面两句:
int age = 45;
age + 10 * 2;
这两个语句里面的语法特性包含了变量声明、给变量赋值,以及在表达式里引用变量。为了给变量赋值,我们必须在脚本语言的解释器中开辟一个存储区,记录不同的变量和它们的值:
private HashMap<String, Integer> variables = new HashMap<String, Integer>();
我们简单地用了一个HashMap作为变量存储区。在变量声明语句和赋值语句里,都可以修改这个变量存储区中的数据,而获取变量值可以采用下面的代码:
if (variables.containsKey(varName)) {
Integer value = variables.get(varName); //获取变量值
if (value != null) {
result = value; //设置返回值
} else { //有这个变量,没有值
throw new Exception("variable " + varName + " has not been set any value");
}
}
else{ //没有这个变量。
throw new Exception("unknown variable: " + varName);
}
通过这样的一个简单的存储机制,我们就能支持变量了。当然,这个存储机制可能过于简单了,我们后面讲到作用域的时候,这么简单的存储机制根本不够。不过目前我们先这么用着,以后再考虑改进它。
接下来,我们来解析赋值语句,例如“age = age + 10 * 2;”:
private SimpleASTNode assignmentStatement(TokenReader tokens) throws Exception {
SimpleASTNode node = null;
Token token = tokens.peek(); //预读,看看下面是不是标识符
if (token != null && token.getType() == TokenType.Identifier) {
token = tokens.read(); //读入标识符
node = new SimpleASTNode(ASTNodeType.AssignmentStmt, token.getText());
token = tokens.peek(); //预读,看看下面是不是等号
if (token != null && token.getType() == TokenType.Assignment) {
tokens.read(); //取出等号
SimpleASTNode child = additive(tokens);
if (child == null) { //出错,等号右面没有一个合法的表达式
throw new Exception("invalide assignment statement, expecting an expression");
}
else{
node.addChild(child); //添加子节点
token = tokens.peek(); //预读,看看后面是不是分号
if (token != null && token.getType() == TokenType.SemiColon) {
tokens.read(); //消耗掉这个分号
} else { //报错,缺少分号
throw new Exception("invalid statement, expecting semicolon");
}
}
}
else {
tokens.unread(); //回溯,吐出之前消化掉的标识符
node = null;
}
}
return node;
}
为了方便你理解,我来解读一下上面这段代码的逻辑:
我们既然想要匹配一个赋值语句,那么首先应该看看第一个Token是不是标识符。如果不是,那么就返回null,匹配失败。如果第一个Token确实是标识符,我们就把它消耗掉,接着看后面跟着的是不是等号。如果不是等号,那证明我们这个不是一个赋值语句,可能是一个表达式什么的。那么我们就要回退刚才消耗掉的Token,就像什么都没有发生过一样,并且返回null。回退的时候调用的方法就是unread()。
如果后面跟着的确实是等号,那么在继续看后面是不是一个表达式,表达式后面跟着的是不是分号。如果不是,就报错就好了。这样就完成了对赋值语句的解析。
利用上面的代码,我们还可以改造一下变量声明语句中对变量初始化的部分,让它在初始化的时候支持表达式,因为这个地方跟赋值语句很像,例如“int newAge = age + 10 * 2;”。
不知道你有没有发现,我在设计语法规则的过程中,其实故意设计了一个陷阱,这个陷阱能帮我们更好地理解递归下降算法的一个特点:回溯。理解这个特点能帮助你更清晰地理解递归下降算法的执行过程,从而再去想办法优化它。
考虑一下age = 45;这个语句。肉眼看过去,你马上知道它是个赋值语句,但是当我们用算法去做模式匹配时,就会发生一些特殊的情况。看一下我们对statement语句的定义:
statement
: intDeclaration
| expressionStatement
| assignmentStatement
;
我们首先尝试intDeclaration,但是age = 45;语句不是以int开头的,所以这个尝试会返回null。然后我们接着尝试expressionStatement,看一眼下面的算法:
private SimpleASTNode expressionStatement() throws Exception {
int pos = tokens.getPosition(); //记下初始位置
SimpleASTNode node = additive(); //匹配加法规则
if (node != null) {
Token token = tokens.peek();
if (token != null && token.getType() == TokenType.SemiColon) { //要求一定以分号结尾
tokens.read();
} else {
node = null;
tokens.setPosition(pos); // 回溯
}
}
return node;
}
出现了什么情况呢?age = 45;语句最左边是一个标识符。根据我们的语法规则,标识符是一个合法的addtiveExpresion,因此additive()函数返回一个非空值。接下来,后面应该扫描到一个分号才对,但是显然不是,标识符后面跟的是等号,这证明模式匹配失败。
失败了该怎么办呢?我们的算法一定要把Token流的指针拨回到原来的位置,就像一切都没发生过一样。因为我们不知道addtive()这个函数往下尝试了多少步,因为它可能是一个很复杂的表达式,消耗掉了很多个Token,所以我们必须记下算法开始时候的位置,并在失败时回到这个位置。尝试一个规则不成功之后,恢复到原样,再去尝试另外的规则,这个现象就叫做“回溯”。
因为有可能需要回溯,所以递归下降算法有时会做一些无用功。在assignmentStatement的算法中,我们就通过unread(),回溯了一个Token。而在expressionStatement中,我们不确定要回溯几步,只好提前记下初始位置。匹配expressionStatement失败后,算法去尝试匹配assignmentStatement。这次获得了成功。
试探和回溯的过程,是递归下降算法的一个典型特征。通过上面的例子,你应该对这个典型特征有了更清晰的理解。递归下降算法虽然简单,但它通过试探和回溯,却总是可以把正确的语法匹配出来,这就是它的强大之处。当然,缺点是回溯会拉低一点儿效率。但我们可以在这个基础上进行改进和优化,实现带有预测分析的递归下降,以及非递归的预测分析。有了对递归下降算法的清晰理解,我们去学习其他的语法分析算法的时候,也会理解得更快。
我们接着再讲回溯牵扯出的另一个问题:什么时候该回溯,什么时候该提示语法错误?
大家在阅读示例代码的过程中,应该发现里面有一些错误处理的代码,并抛出了异常。比如在赋值语句中,如果等号后面没有成功匹配一个加法表达式,我们认为这个语法是错的。因为在我们的语法中,等号后面只能跟表达式,没有别的可能性。
token = tokens.read(); //读出等号
node = additive(); //匹配一个加法表达式
if (node == null) {
//等号右边一定需要有另一个表达式
throw new Exception("invalide assignment expression, expecting an additive expression");
}
你可能会意识到一个问题,当我们在算法中匹配不成功的时候,我们前面说的是应该回溯呀,应该再去尝试其他可能性呀,为什么在这里报错了呢?换句话说,什么时候该回溯,什么时候该提示这里发生了语法错误呢?
其实这两种方法最后的结果是一样的。我们提示语法错误的时候,是说我们知道已经没有其他可能的匹配选项了,不需要浪费时间去回溯。就比如,在我们的语法中,等号后面必然跟表达式,否则就一定是语法错误。你在这里不报语法错误,等试探完其他所有选项后,还是需要报语法错误。所以说,提前报语法错误,实际上是我们写算法时的一种优化。
在写编译程序的时候,我们不仅仅要能够解析正确的语法,还要尽可能针对语法错误提供友好的提示,帮助用户迅速定位错误。错误定位越是准确、提示越是友好,我们就越喜欢它。
好了,到目前为止,已经能够能够处理几种不同的语句,如变量声明语句,赋值语句、表达式语句,那么我们把所有这些成果放到一起,来体会一下使用自己的脚本语言的乐趣吧!
我们需要一个交互式的界面来输入程序,并执行程序,这个交互式的界面就叫做REPL。
脚本语言一般都会提供一个命令行窗口,让你输入一条一条的语句,马上解释执行它,并得到输出结果,比如Node.js、Python等都提供了这样的界面。这个输入、执行、打印的循环过程就叫做REPL(Read-Eval-Print Loop)。你可以在REPL中迅速试验各种语句,REPL即时反馈的特征会让你乐趣无穷。所以,即使是非常资深的程序员,也会经常用REPL来验证自己的一些思路,它相当于一个语言的PlayGround(游戏场),是个必不可少的工具。
在SimpleScript.java中,我们也实现了一个简单的REPL。基本上就是从终端一行行的读入代码,当遇到分号的时候,就解释执行,代码如下:
SimpleParser parser = new SimpleParser();
SimpleScript script = new SimpleScript();
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in)); //从终端获取输入
String scriptText = "";
System.out.print("\n>"); //提示符
while (true) { //无限循环
try {
String line = reader.readLine().trim(); //读入一行
if (line.equals("exit();")) { //硬编码退出条件
System.out.println("good bye!");
break;
}
scriptText += line + "\n";
if (line.endsWith(";")) { //如果没有遇到分号的话,会再读一行
ASTNode tree = parser.parse(scriptText); //语法解析
if (verbose) {
parser.dumpAST(tree, "");
}
script.evaluate(tree, ""); //对AST求值,并打印
System.out.print("\n>"); //显示一个提示符
scriptText = "";
}
} catch (Exception e) { //如果发现语法错误,报错,然后可以继续执行
System.out.println(e.getLocalizedMessage());
System.out.print("\n>"); //提示符
scriptText = "";
}
}
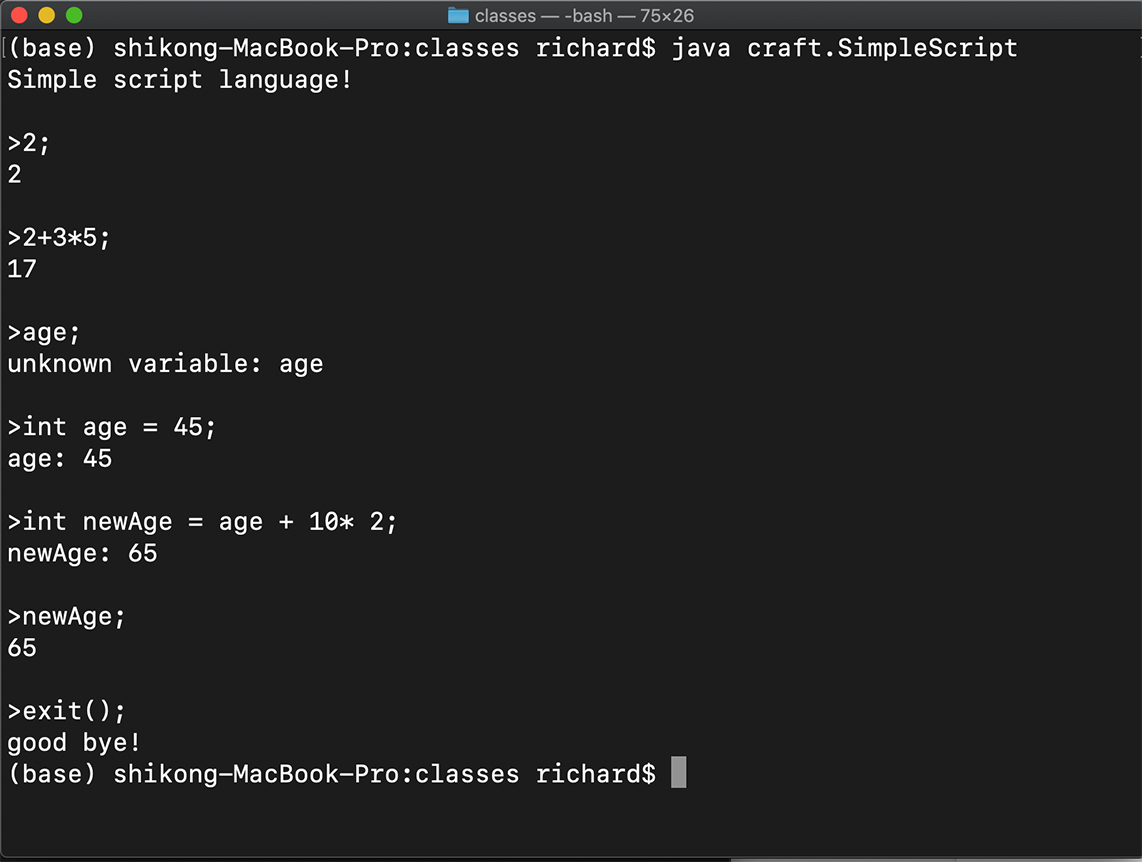
运行java craft.SimpleScript,你就可以在终端里尝试各种语句了。如果是正确的语句,系统马上会反馈回结果。如果是错误的语句,REPL还能反馈回错误信息,并且能够继续处理下面的语句。我们前面添加的处理语法错误的代码,现在起到了作用!下面是在我电脑上的运行情况:

如果你用java craft.SimpleScript -v启动REPL,则进入Verbose模式,它还会每次打印出AST,你可以尝试一下。
退出REPL需要在终端输入ctl+c,或者调用exit()函数。我们目前的解释器并没有支持函数,所以我们是在REPL里硬编码来实现exit()函数的。后面的课程里,我会带你真正地实现函数特性。
我希望你能编译一下这个程序,好好的玩一玩它,然后再修改一下源代码,增加一些你感兴趣的特性。我们学习跟打游戏一样,好玩、有趣才能驱动我们不停地学下去,一步步升级打怪。我个人觉得,我们作为软件工程师,拿出一些时间来写点儿有趣的东西作为消遣,乐趣和成就感也是很高的,况且还能提高水平。
本节课我们通过对三种语句的支持,实现了一个简单的脚本语言。REPL运行代码的时候,你会有一种真真实实的感觉,这确实是一门脚本语言了,虽然它没做性能的优化,但你运行的时候也还觉得挺流畅。
学完这讲以后,你也能找到了一点感觉:Shell脚本也好,PHP也好,JavaScript也好,Python也好,其实都可以这样写出来。
回顾过去几讲,你已经可以分析词法、语法、进行计算,还解决了左递归、优先级、结合性的问题。甚至,你还能处理语法错误,让脚本解释器不会因为输入错误而崩溃。
想必这个时候你已经开始相信我的承诺了:每个人都可以写一个编译器。这其实也是我最想达到的效果。相信自己,只要你不给自己设限,不设置玻璃天花板,其实你能够做出很多让自己惊讶、让自己骄傲的成就。
收获对自己的信心,掌握编译技术,将是你学习这门课程后最大的收获!
本节课,我们设计了一个可能导致递归下降算法中回溯的情景。在你的计算机语言中,有哪些语法在运用递归下降算法的时候,也是会导致回溯的?
如果你还想进一步挑战自己,可以琢磨一下,递归下降算法的回溯,会导致多少计算时间的浪费?跟代码长度是线性关系还是指数关系?我们在后面梳理算法的时候,会涉及到这个问题。
欢迎在留言区里分享你的发现,与大家一起讨论。最后,感谢你的阅读,如果这篇文章让你有所收获,也欢迎你将它分享给更多的朋友。
另外,第2讲到第5讲的代码,都在代码库中的lab子目录的craft子目录下,代码库在码云和GitHub上都有,希望你能下载玩一玩。
评论