在前面的课程中,我讲了递归下降算法。这个算法很常用,但会有回溯的现象,在性能上会有损失。所以我们要把算法升级一下,实现带有预测能力的自顶向下分析算法,避免回溯。而要做到这一点,就需要对自顶向下算法有更全面的了解。
另外,在留言区,有几个同学问到了一些问题,涉及到对一些基本知识点的理解,比如:
要搞清这些问题,也需要全面了解自顶向下算法。比如,了解Follow集合和$符号的用法,能帮你解决第一个问题;了解广度优先算法能帮你解决第二个问题。
所以,本节课,我先把自顶向下分析的算法体系梳理一下,让你先建立更加清晰的全景图,然后我再深入剖析LL算法的原理,讲清楚First集合与Follow集合这对核心概念,最终让你把自顶向下的算法体系吃透。
自顶向下分析的算法是一大类算法。总体来说,它是从一个非终结符出发,逐步推导出跟被解析的程序相同的Token串。
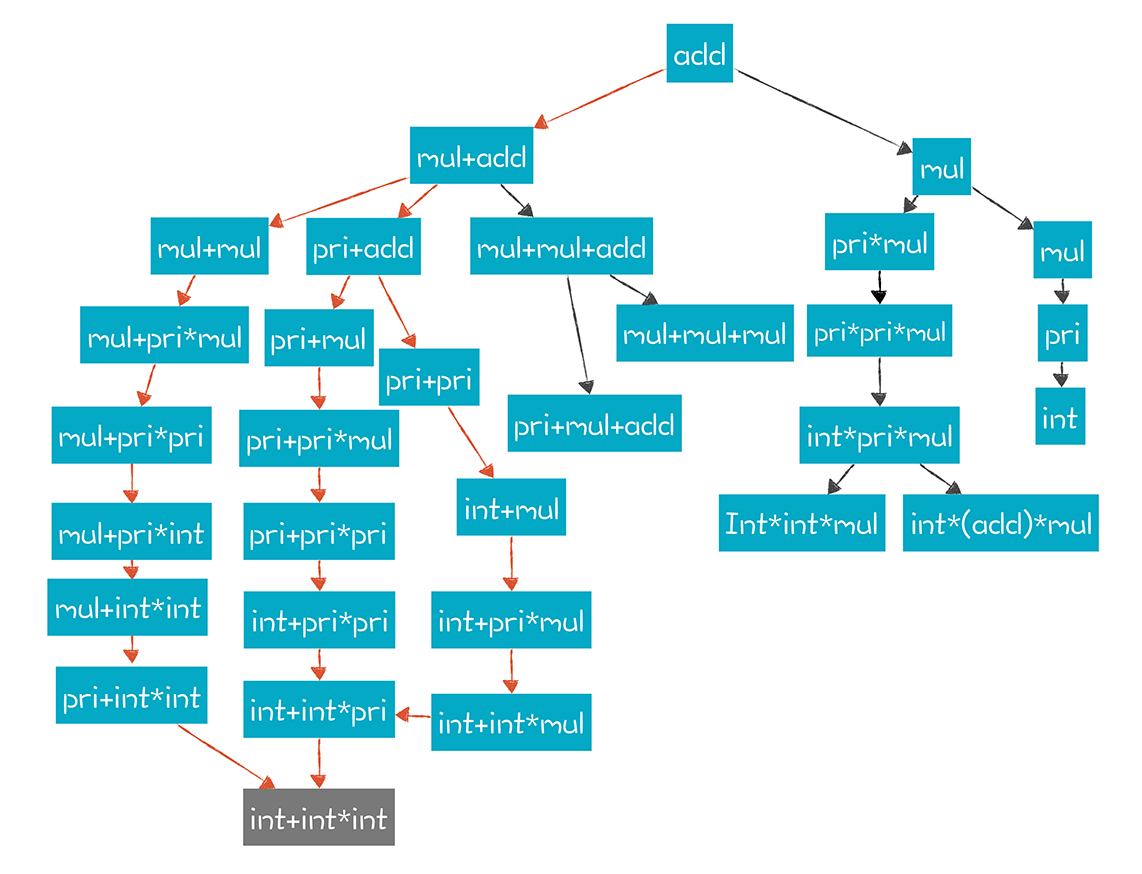
这个过程可以看做是一张图的搜索过程,这张图非常大,因为针对每一次推导,都可能产生一个新节点。下面这张图只是它的一个小角落。

算法的任务,就是在大图中,找到一条路径,能产生某个句子(Token串)。比如,我们找到了三条橘色的路径,都能产生“2+3*5”这个表达式。
根据搜索的策略,有深度优先(Depth First)和广度优先(Breadth First)两种,这两种策略的推导过程是不同的。
深度优先是沿着一条分支把所有可能性探索完。以“add->mul+add”产生式为例,它会先把mul这个非终结符展开,比如替换成pri,然后再把它的第一个非终结符pri展开。只有把这条分支都向下展开之后,才会回到上一级节点,去展开它的兄弟节点。
递归下降算法就是深度优先的,这也是它不能处理左递归的原因,因为左边的分支永远也不能展开完毕。
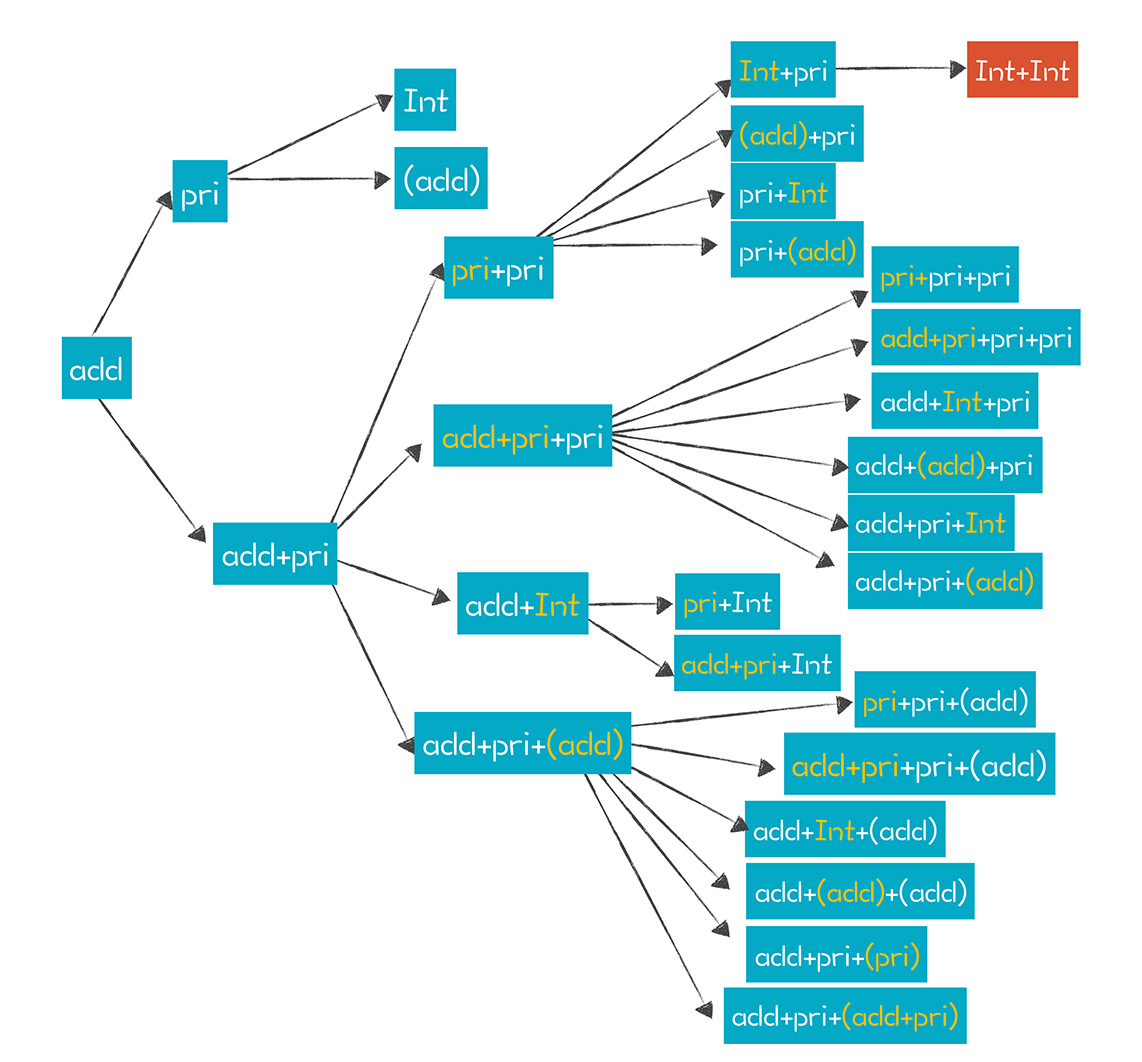
而针对“add->add+mul”这个产生式,广度优先会把add和mul这两个都先展开,这样就形成了四条搜索路径,分别是mul+mul、add+mul+mul、add+pri和add+mul*pri。接着,把它们的每个非终结符再一次展开,会形成18条新的搜索路径。
所以,广度优先遍历,需要探索的路径数量会迅速爆炸,成指数级上升。哪怕用下面这个最简单的语法,去匹配“2+3”表达式,都需要尝试20多次,更别提针对更复杂的表达式或者采用更加复杂的语法规则了。
//一个很简单的语法
add -> pri //1
add -> add + pri //2
pri -> Int //3
pri -> (add) //4
这样看来,指数级上升的内存消耗和计算量,使得广度优先根本没有实用价值。虽然上面的算法有优化空间,但无法从根本上降低算法复杂度。当然了,它也有可以使用左递归文法的优点,不过我们不会为了这个优点去忍受算法的性能。
而深度优先算法在内存占用上是线性增长的。考虑到回溯的情况,在最坏的情况下,它的计算量也会指数式增长,但我们可以通过优化,让复杂度降为线性增长。
了解广度优先算法,你的思路会得到拓展,对自顶向下算法的本质有更全面的理解。另外,在写算法时,你也不会一会儿用深度优先,一会儿用广度优先了。
针对深度优先算法的优化方向是减少甚至避免回溯,思路就是给算法加上预测能力。比如,我在解析statement的时候,看到一个if,就知道肯定这是一个条件语句,不用再去尝试其他产生式了。
LL算法就属于这类预测性的算法。第一个L,是Left-to-right,代表从左向右处理程序代码。第二个L,是Leftmost,意思是最左推导。
按照语法规则,一个非终结符展开后,会形成多个子节点,其中包含终结符和非终结符。最左推导是指,从左到右依次推导展开这些非终结符。采用Leftmost的方法,在推导过程中,句子的左边逐步都会被替换成终结符,只有右边的才可能包含非终结符。
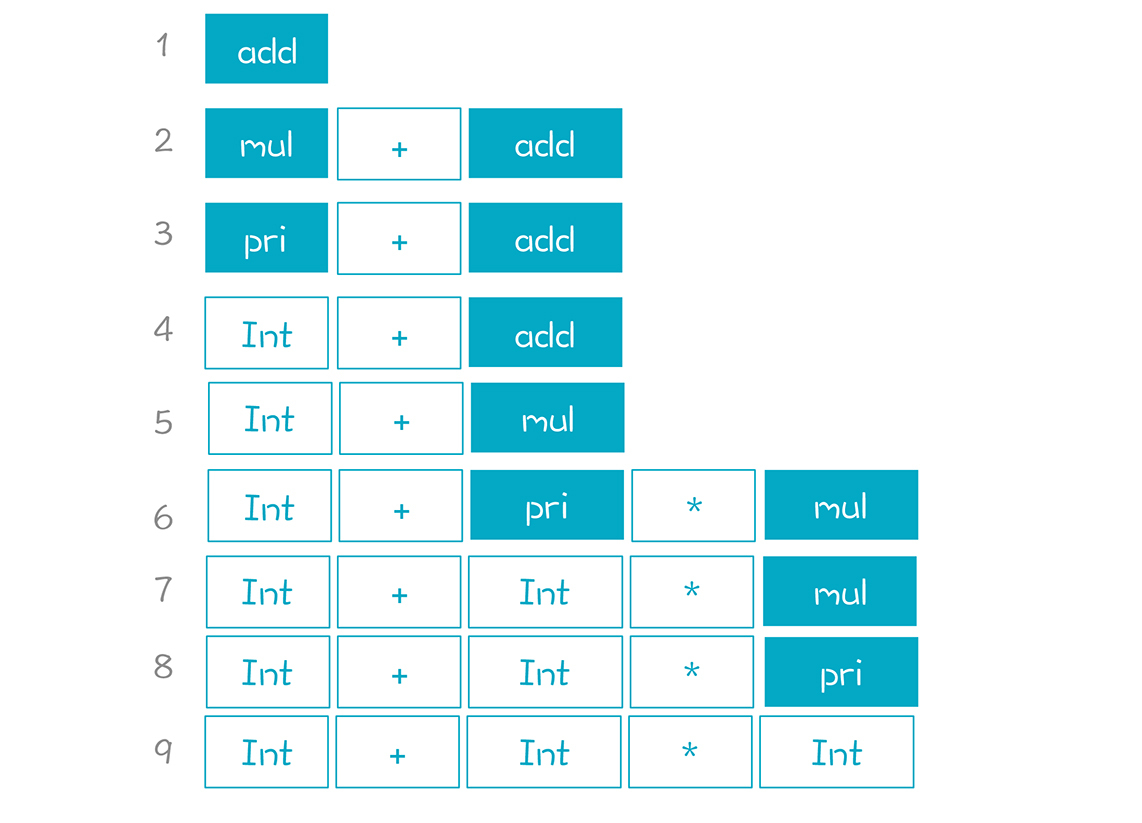
以“2+3*5”为例,它的推导顺序从左到右,非终结符逐步替换成了终结符:
下图是上述推导过程建立起来的AST,“1、2、3……”等编号是AST节点创建的顺序:
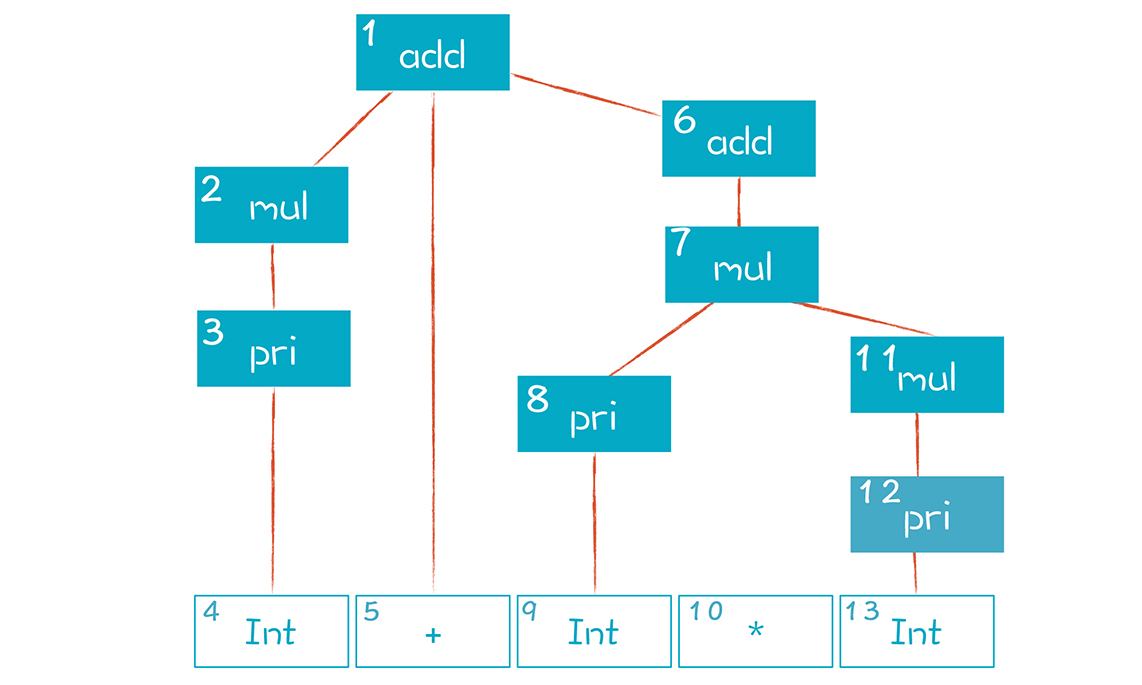
好了,我们把自顶向下分析算法做了总体概述,并讲清楚了最左推导的含义,现在来看看LL算法到底是怎么回事。
LL算法是带有预测能力的自顶向下算法。在推导的时候,我们希望当存在多个候选的产生式时,瞄一眼下一个(或多个)Token,就知道采用哪个产生式。如果只需要预看一个Token,就是LL(1)算法。
拿statement的语法举例子,它有好几个产生式,分别产生if语句、while语句、switch语句……
statement
: block
| IF parExpression statement (ELSE statement)?
| FOR '(' forControl ')' statement
| WHILE parExpression statement
| DO statement WHILE parExpression ';'
| SWITCH parExpression '{' switchBlockStatementGroup* switchLabel*
| RETURN expression? ';'
| BREAK IDENTIFIER? ';'
| CONTINUE IDENTIFIER? ';'
| SEMI
| statementExpression=expression ';'
| identifierLabel=IDENTIFIER ':' statement
;
如果我看到下一个Token是if,那么后面跟着的肯定是if语句,这样就实现了预测,不需要一个一个产生式去试。
问题来了,if语句的产生式的第一个元素就是一个终结符,这自然很好判断,可如果是一个非终结符,比如表达式语句,那该怎么判断呢?
我们可以为statement的每条分支计算一个集合,集合包含了这条分支所有可能的起始Token。如果每条分支的起始Token是不一样的,也就是这些集合的交集是空集,那么就很容易根据这个集合来判断该选择哪个产生式。我们把这样的集合,就叫做这个产生式的First集合。
First集合的计算很直观,假设我们要计算的产生式是x:
blockStatements
: blockStatement*
;
在本讲的示例程序里,我们可以用SampleGrammar.expressionGrammar()方法获得一个表达式的语法,把它dump()一下,这其实是消除了左递归的表达式语法:
expression : assign ;
assign : equal | assign1 ;
assign1 : '=' equal assign1 | ε;
equal : rel equal1 ;
equal1 : ('==' | '!=') rel equal1 | ε ;
rel : add rel1 ;
rel1 : ('>=' | '>' | '<=' | '<') add rel1 | ε ;
add : mul add1 ;
add1 : ('+' | '-') mul add1 | ε ;
mul : pri mul1 ;
mul1 : ('*' | '/') pri mul1 | ε ;
pri : ID | INT_LITERAL | LPAREN expression RPAREN ;
我们用GrammarNode类代表语法的节点,形成一张语法图(蓝色节点的下属节点之间是“或”的关系,也就是语法中的竖线)。
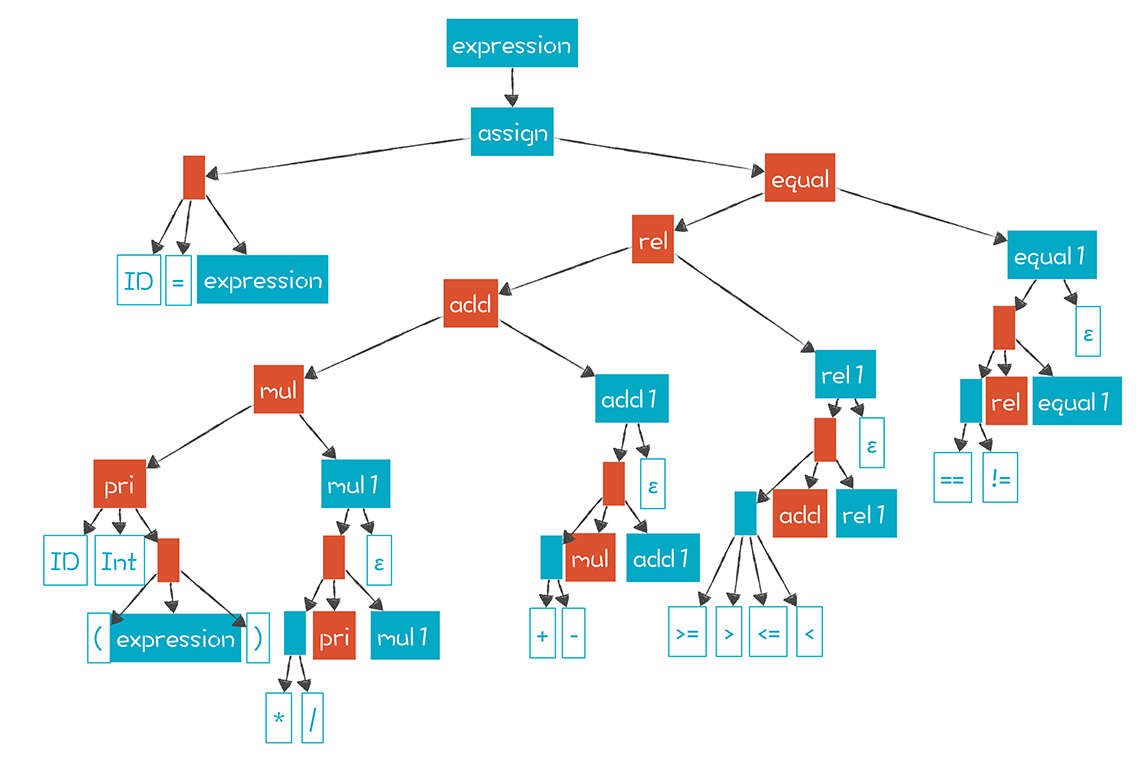
基于这个数据结构能计算每个非终结符的First集合,可以参考LLParser类的caclFirstSets()方法。运行示例程序可以打印出表达式语法中各个非终结符的First集合。
在计算时你要注意,因为上下文无关文法是允许递归嵌套的,所以这些GrammarNode节点构成的是一个图,而不是树,不能通过简单的遍历树的方法来计算First集合。比如,pri节点是expression的后代节点,但pri又引用了expression(pri->(expression))。这样,计算First(expression)需要用到First(pri),而计算First(pri)又需要依赖First(expression)。
破解这个僵局的方法是用“不动点法”来计算。多次遍历图中的节点,看看每次有没有计算出新的集合成员。比如,第一遍计算的时候,当求First(pri)的时候,它所依赖的First(expression)中的成员可能不全,等下一轮继续计算时,发现有新的集合成员,再加进来就好了,直到所有集合的成员都没有变动为止。
现在我们可以用First集合进行分支判断了,不过还要处理产生式可能为ε的情况,比如“+mul add1 | ε”或“blockStatement*”都会产生ε。
对ε的处理分成两种情况。
第一种情况,是产生式中的部分元素会产生ε。比如,在Java语法里,声明一个类成员的时候,可能会用public、private这些来修饰,但也可以省略不写。在语法规则中,这个部分是“accessModifier?”,它就可能产生ε。
memberDeclaration : accessModifier? type identifier ';' ;
accessModifier : 'public' | 'private' ;
type : 'int' | 'long' | 'double' ;
所以,当我们遇到下面这两个语句的时候,都可以判断为类成员的声明:
public int a;
int b;
这时,type能够产生的终结符 ‘int’、‘long’和‘double’也在memberDeclaration的First集合中。这样,我们实际上把accessModifier给穿透了,直接到了下一个非终结符type。所以这类问题依靠First集合仍然能解决。在解析的过程中,如果下一个Token是 ‘int’,我们可以认为accessModifier返回了ε,忽略它,继续解析下一个元素type,因为它的First集合中才会包含 ‘int’。
第二种情况是产生式本身(而不是其组成部分)产生ε。这类问题仅仅依靠First集合是无法解决的,要引入另一个集合:Follow集合。它是所有可能跟在某个非终结符之后的终结符的集合。
以block语句为例,在PlayScript.g4中,大致是这样定义的:
block
: '{' blockStatements '}'
;
blockStatements
: blockStatement*
;
blockStatement
: variableDeclarators ';'
| statement
| functionDeclaration
| classDeclaration
;
也就是说,block是由blockStatements构成的,而blockStatements可以由0到n个blockStatement构成,因此可能产生ε。
接下来,我们来看看解析block时会发生什么。
假设花括号中一个语句也没有,也就是blockStatments实际上产生了ε。那么在解析block时,首先读取了一个Token,即“{”,然后处理blockStatements,我们再预读一个Token,发现是“}”,那这个右花括号是blockStatement的哪个产生式的呢?实际上它不在任何一个产生式的First集合中,下面是进行判断的伪代码:
nextToken = tokens.peek(); //得到'}'
nextToken in First(variableDeclarators) ? //no
nextToken in First(statement) ? //no
nextToken in First(functionDeclaration) ? //no
nextToken in First(classDeclaration) ? //no
我们找不到任何一个可用的产生式。这可怎么办呢?除了可能是blockStatments本身产生了ε之外,还有一个可能性就是出现语法错误了。而要继续往下判断,就需要用到Follow集合。
像blockStatements的Follow集合只有一个元素,就是右花括号“}”。所以,我们只要再检查一下nextToken是不是花括号就行了:
//伪代码
nextToken = tokens.peek(); //得到'}'
nextToken in First(variableDeclarators) ? //no
nextToken in First(statement) ? //no
nextToken in First(functionDeclaration) ? //no
nextToken in First(classDeclaration) ? //no
if (nextToken in Follow(blockStatements)) //检查Follow集合
return Epsilon; //推导出ε
else
error; //语法错误
那么怎么计算非终结符x的Follow集合呢?
这个符号通常记做$,意味一个程序的结束。比如在表达式的语法里,expression 后面可能跟这个符号,expression 的所有右侧分支的后代节点也都可能跟这个符号,也就是它们都可能出现在程序的末尾。但另一些非终结符,后面不会跟这个符号,如blockstatements,因为它后面肯定会有“}”。
你可以参考LLParser类的caclFollowSets()方法,这里也要用到不动点法做计算。运行程序可以打印出示例语法的的Follow集合。我把程序打印输出的First和follow集合整理如下(其实打印输出还包含一些中间节点,这里就不展示了):
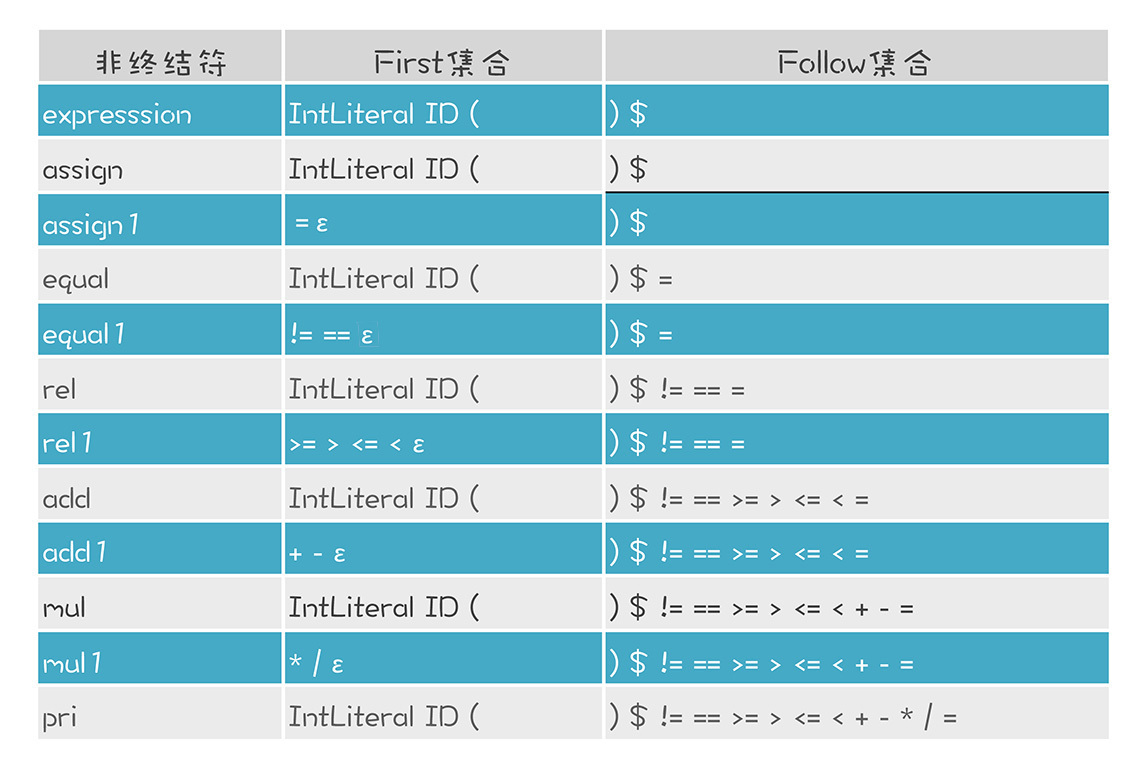
在表达式的解析中,我们会综合运用First和Follow集合。比如,对于“add1 -> + mul add1 | ε”,如果预读的下一个Token是+,那就按照第一个产生式处理,因为+在First(“+ mul add1”)集合中。如果预读的Token是>号,那它肯定不在First(add1)中,而我们要看它是否属于Follow(add1),如果是,那么add1就产生一个ε,否则就报错。
现在我们已经建立了对First集合、Follow集合和LL算法计算过程的直觉认知。这样再写出算法的实现,就比较容易了。用LL算法解析语法的时候,我们可以选择两种实现方式。
第一种,还是采用递归下降算法,只不过现在的递归下降算法是没有任何回溯的。无论走到哪一步,我们都能准确地预测出应该采用哪个产生式。
第二种,是采用表驱动的方式。这个时候需要基于我们计算出来的First和Follow集合构造一张预测分析表。根据这个表,查找在遇到什么Token的情况下,应该走哪条路径。
这两种方式是等价的,你可以根据自己的喜好来选择,我用的是第一种。关于算法,我们就说这么多,接下来,我们谈谈如何设计符合LL(k)特别是LL(1)算法的文法。
我们已经知道左递归的文法是要避免的,也知道要如何避免。除此之外,我们要尽量抽取左公因子,这样可以避免First集合产生交集。举例来说,变量声明和函数声明的规则在前半截都差不多,都是类型后面跟着标识符:
statement : variableDeclare | functionDeclare | other;
variableDeclare : type Identifier ('=' expression)? ;
funcationDeclare : type Identifier '(' parameterList ')' block ;
具体例子如下:
int age;
int cacl(int a, int b){
return a + b;
}
这样的语法规则,如果按照LL(1)算法,First(variableDeclare)和First(funcationDeclare)是相同的,没法决定走哪条路径。你就算用LL(2),也是一样的,要用到LL(3)才行。但对于LL(k) k > 1来说,程序开销有点儿大,因为要计算更多的集合,构造更复杂的预测分析表。
不过这个问题很容易解决,只要把它们的左公因子提出来就可以了:
statement: declarator | other;
declarator : declarePrefix (variableDeclarePostfix
|functionDeclarePostfix) ;
variableDeclarePostfix : ('=' expression)? ;
functionDeclarePostfix : '(' parameterList ')' block ;
这样,解析程序先解析它们的公共部分,即declarePrefix,然后再看后面的差异。这时,它俩的First集合,一个{ = ; },一个是{ ( },两者没有交集,能够很容易区分。
本节课我们比较全面地梳理了自顶向下算法。语法解析过程可以看做是对图的遍历过程,遍历时可以采取深度优先或广度优先的策略,这里要注意,你可能在做深度优先遍历的时候,误用广度优先的思路。
针对LL算法,我们通过实例分析了First集合和Follow集合的使用场景和计算方式。掌握了这两个核心概念,特别是熟悉它们的使用场景,你会彻底掌握LL算法。
处理ε是LL算法中的关键点。在你熟悉的语言中,哪些语法会产生ε,你在做语法解析的时候会怎样处理它们?欢迎在留言区分享你的思考。
最后,感谢你的阅读,如果这篇文章让你有所收获,也欢迎你将它分享给更多的朋友。
本节课的示例代码我放在了文末,供你参考。
评论