
你好,我是宫文学。
通过第1讲的学习,现在你已经清楚了语法分析阶段的任务:依据语法规则,把Token串转化成AST。
今天,我就带你来掌握语法分析阶段的核心知识点,也就是两个基本功和两种算法思路。理解了这些重要的知识点,对于语法分析,你就不是外行了。
在开始语法分析之前,我们要解决的第一个问题,就是如何表达语法规则。在上一讲中,你已经了解了,我们可以用正则表达式来表达词法规则,语法规则其实也差不多。
我还是以下面这个示例程序为例,里面用到了变量声明语句、加法表达式,我们看看语法规则应该怎么写:
int a = 2;
int b = a + 3;
return b;
第一种写法是下面这个样子,它看起来跟上一讲的词法规则差不多,都是左边是规则名称,右边是正则表达式。
start:blockStmts ; //起始
block : '{' blockStmts '}' ; //语句块
blockStmts : stmt* ; //语句块中的语句
stmt = varDecl | expStmt | returnStmt | block; //语句
varDecl : type Id varInitializer? ';' ; //变量声明
type : Int | Long ; //类型
varInitializer : '=' exp ; //变量初始化
expStmt : exp ';' ; //表达式语句
returnStmt : Return exp ';' ; //return语句
exp : add ; //表达式
add : add '+' mul | mul; //加法表达式
mul : mul '*' pri | pri; //乘法表达式
pri : IntLiteral | Id | '(' exp ')' ; //基础表达式
在语法规则里,我们把冒号左边的叫做非终结符(Non-terminal),又叫变元(Variable)。非终结符可以按照右边的正则表达式来逐步展开,直到最后都变成标识符、字面量、运算符这些不可再展开的符号,也就是终结符(Terminal)。终结符其实也是词法分析过程中形成的Token。
提示:
1.在本课程,非终结符以小写字母开头,终结符则以大写字母开头,或者是一个原始的字符串格式。
2.在谈论语法分析的时候,我们可以把Token和终结符这两个术语互换使用。
像这样左边是非终结符,右边是正则表达式的书写语法规则的方式,就叫做扩展巴科斯范式(EBNF)。你在ANTLR这样的语法分析器生成工具中,经常会看到这种格式的语法规则。
对于EBNF的严格定义,你可以去参考Wikipedia上的解释。
在教科书中,我们还经常采用另一种写法,就是产生式(Production Rule),又叫做替换规则(Substitution Rule)。产生式的左边是非终结符(变元),它可以用右边的部分替代,中间通常会用箭头连接。
为了避免跟EBNF中的“*”号、“+”号等冲突,在本节课中,凡是采用EBNF格式,就给字符串格式的终结符加引号,左右两边用“::=”或冒号分隔开;凡是采用产生式,字符串就不加引号,并且采用“->”分隔产生式的左右两侧。
add -> add + mul
add -> mul
mul -> mul * pri
mul -> pri
也有个偷懒的写法,就是把同一个变元的多个产生式写在一起,用竖线分隔(但这时候,如果产生式里面原本就要用到“|”终结符,那么就要加引号来进行区分)。但也就仅此为止了,不会再引入“*”和“+”等符号,否则就成了EBNF了。
add -> add + mul | mul
mul -> mul * pri | pri
产生式不用“ * ”和“+”来表示重复,而是用迭代,并引入“ε”(空字符串)。所以“blockStmts : stmt*”可以写成下面这个样子:
blockStmts -> stmt blockStmts | ε
总结起来,语法规则是由4个部分组成的:
那么符合这四个特点的文法规则,就叫做上下文无关文法(Context-Free Grammar,CFG)。
你可能会问,上下文无关文法和词法分析中用到的正则文法是否有一定的关系?
是的,正则文法是上下文无关文法的一个子集。其实,正则文法也可以写成产生式的格式。比如,数字字面量(正则表达式为“[0-9]+”)可以写成:
IntLiteral -> Digit IntLiteral1
IntLiteral1 -> Digit IntLiteral1
IntLiteral1 -> ε
Digit -> [0-9]
但是,在上下文无关文法里,产生式的右边可以放置任意的终结符和非终结符,而正则文法只是其中的一个子集,叫做线性文法(Linear Grammar)。它的特点是产生式的右边部分最多只有一个非终结符,比如X->aYb,其中a和b是终结符。

你可以试一下,把上一讲用到的正则表达式“a[a-zA-Z0-9]*bc”写成产生式的格式,它就符合线性文法的特点。
S0 -> aS1bc
S1 -> [a-zA-Z0-9]S1
S1 -> ε
但对于常见的语法规则来说,正则文法是不够的。比如,你最常用的算术表达式的规则,就没法用正则文法表示,因为有的产生式需要包含两个非终结符(如“add + mul”)。你可以试试看,能把“2+3”“2+3*5”“2+3+4+5”等各种可能的算术表达式,用一个正则表达式写出来吗?实际是不可能的。
add -> add + mul
add -> mul
mul -> mul * pri
mul -> pri
好,现在你已经了解了上下文无关文法,以及它与正则文法的区别。可是,为什么它会叫“上下文无关文法”这样一个奇怪的名字呢?难道还有上下文相关的文法吗?
答案的确是有的。举个例子来说,在高级语言里,本地变量必须先声明,才能在后面使用。这种制约关系就是上下文相关的。
不过,在语法分析阶段,我们一般不管上下文之间的依赖关系,这样能使得语法分析的任务更简单。而对于上下文相关的情况,则放到语义分析阶段再去处理。
好了,现在你已经知道,用上下文无关文法可以描述程序的语法结构。学习编译原理,阅读和书写语法规则是一项基本功。针对高级语言中的各种语句,你要都能够手写出它们的语法规则来才可以。
接下来,我们就要依据语法规则,编写语法分析程序,把Token串转化成AST。语法分析的算法有很多,但有一个算法也是你必须掌握的一项基本功,这就是递归下降算法。
递归下降算法其实很简单,它的基本思路就是按照语法规则去匹配Token串。比如说,变量声明语句的规则如下:
varDecl : types Id varInitializer? ';' ; //变量声明
varInitializer : '=' exp ; //变量初始化
exp : add ; //表达式
add : add '+' mul | mul; //加法表达式
mul : mul '*' pri | pri; //乘法表达式
pri : IntLiteral | Id | '(' exp ')' ; //基础表达式
如果写成产生式格式,是下面这样:
varDecl -> types Id varInitializer ';'
varInitializer -> '=' exp
varInitializer -> ε
exp -> add
add -> add + mul
add -> mul
mul -> mul * pri
mul -> pri
pri -> IntLiteral
pri -> Id
pri -> ( exp )
而基于这个规则做解析的算法如下:
匹配一个数据类型(types)
匹配一个标识符(Id),作为变量名称
匹配初始化部分(varInitializer),而这会导致下降一层,使用一个新的语法规则:
匹配一个等号
匹配一个表达式(在这个步骤会导致多层下降:exp->add->mul->pri->IntLiteral)
创建一个varInitializer对应的AST节点并返回
如果没有成功地匹配初始化部分,则回溯,匹配ε,也就是没有初始化部分。
匹配一个分号
创建一个varDecl对应的AST节点并返回
用上述算法解析“int a = 2”,就会生成下面的AST:
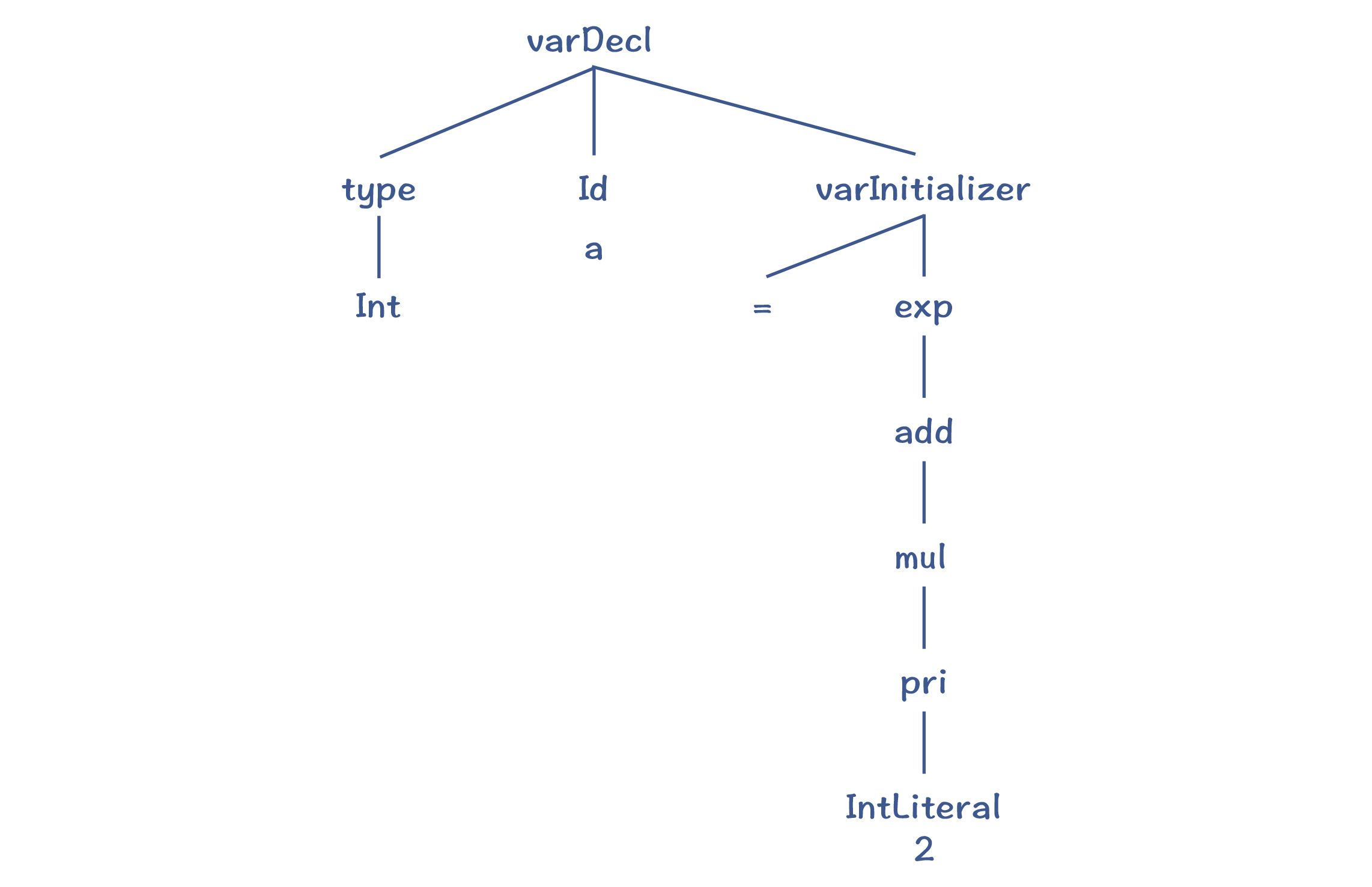
那么总结起来,递归下降算法的特点是:
所以说,递归下降算法是非常容易理解的。它能非常有效地处理很多语法规则,但是它也有两个缺点。
第一个缺点,就是著名的左递归(Left Recursion)问题。比如,在匹配算术表达式时,产生式的第一项就是一个非终结符add,那么按照算法,要下降一层,继续匹配add。这个过程会一直持续下去,无限递归下去。
add -> add + mul
所以,递归下降算法是无法处理左递归问题的。那么有什么解决办法吗?
你可能会说,把产生式改成右递归不就可以了吗?也就是add这个递归项在右边:
add -> mul + add
这样确实可以避免左递归问题,但它同时也会导致结合性的问题。
举个例子来说,我们按照上面的语法规则来解析“2+3+4”这个表达式,会形成如下所示的AST。
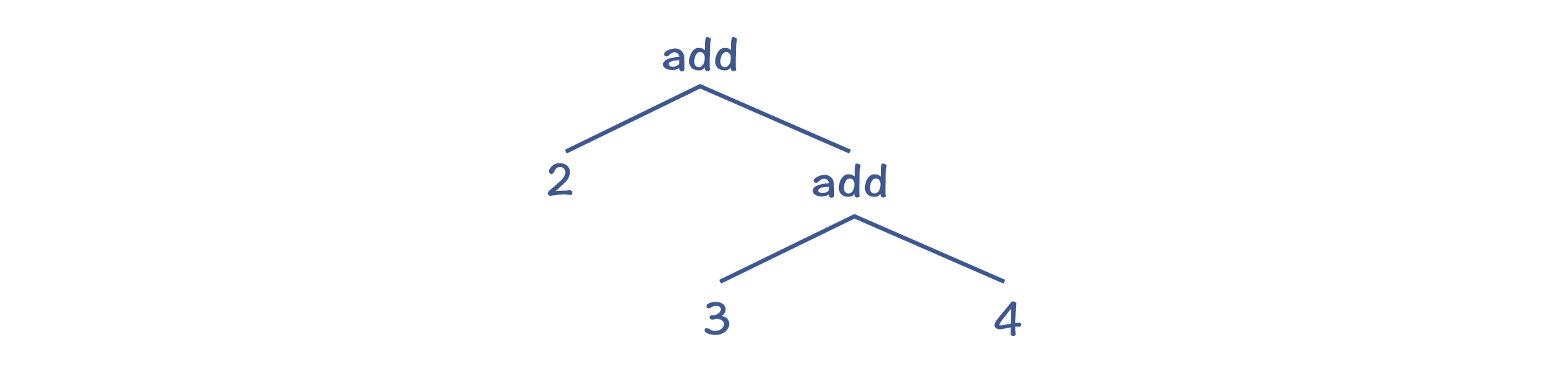
它会先计算“3+4”,而不是先计算“2+3”。这破坏了加法的结合性规则,加法运算本来应该是左结合的。
其实有一个标准的方法,能避免左递归问题。我们可以改写原来的语法规则,也就是引入add',把左递归变成右递归:
add -> mul add'
add' -> + mul add' | ε
接下来,我们用刚刚改写的规则再次解析一下 “2+3+4”这个表达式,会得到下图中的AST:
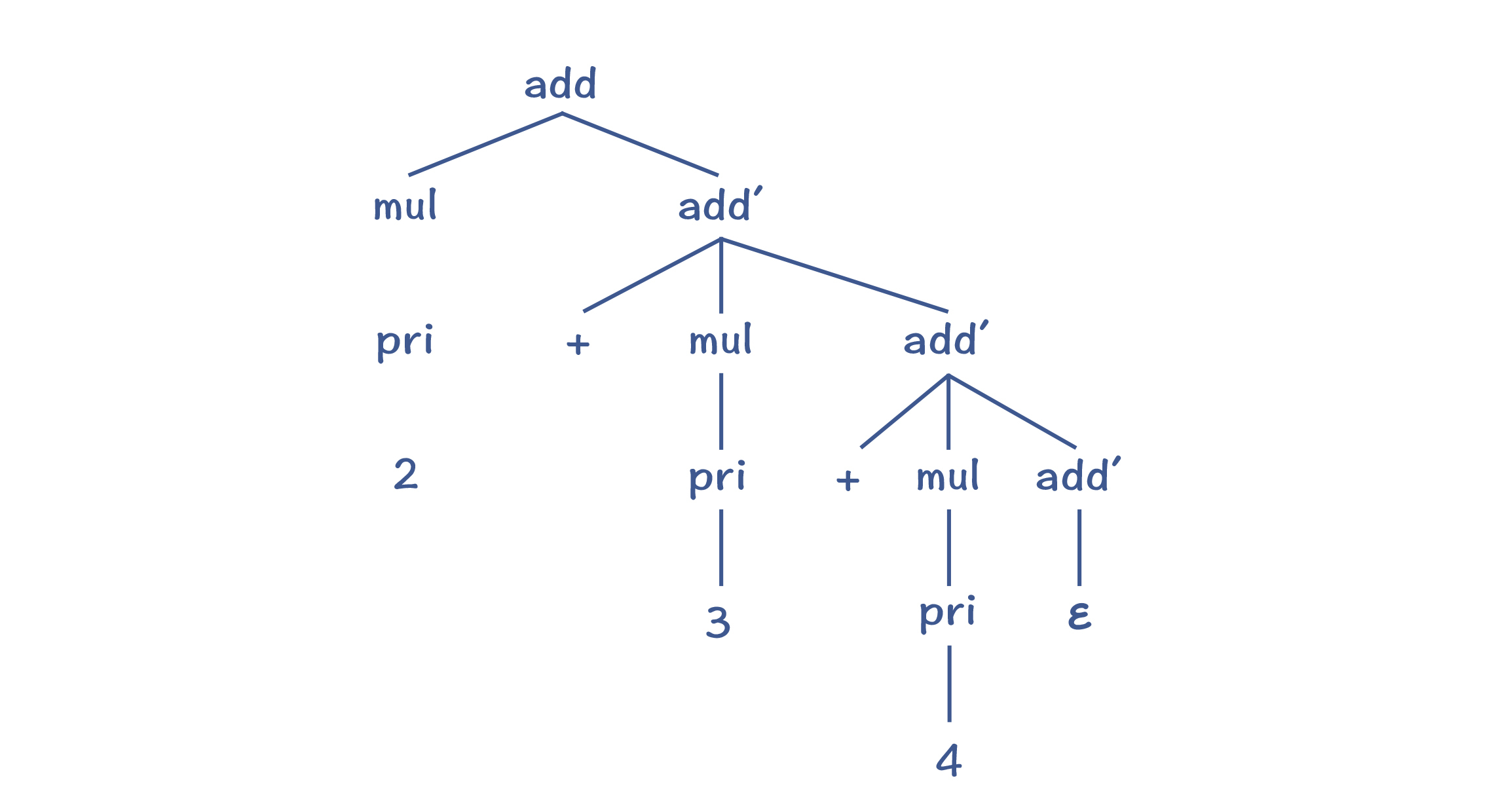
你能看出,这种改写方法虽然能够避免左递归问题,但由于add'的规则是右递归的,采用标准的递归下降算法,仍然会出现运算符结合性的错误。那么针对这点,我们有没有解决办法呢?
有的,方法就是把递归调用转化成循环。这里利用了很多同学都知道的一个原理,即递归调用可以转化为循环。
其实我把上面的规则换成用EBNF方式来表达就很清楚了。在EBNF格式里,允许用“*”号和“+”号表示重复:
add : mul ('+' mul)* ;
所以说,对于('+'mul)*这部分,我们其实可以写成一个循环。而在循环里,我们可以根据结合性的要求,手工生成正确的AST。它的伪代码如下:
左子节点 = 匹配一个mul
while(下一个Token是+){
消化掉+
右子节点 = 匹配一个mul
用左、右子节点创建一个add节点
左子节点 = 该add节点
}
采用上面的算法,就可以创建正确的AST,如下图所示:
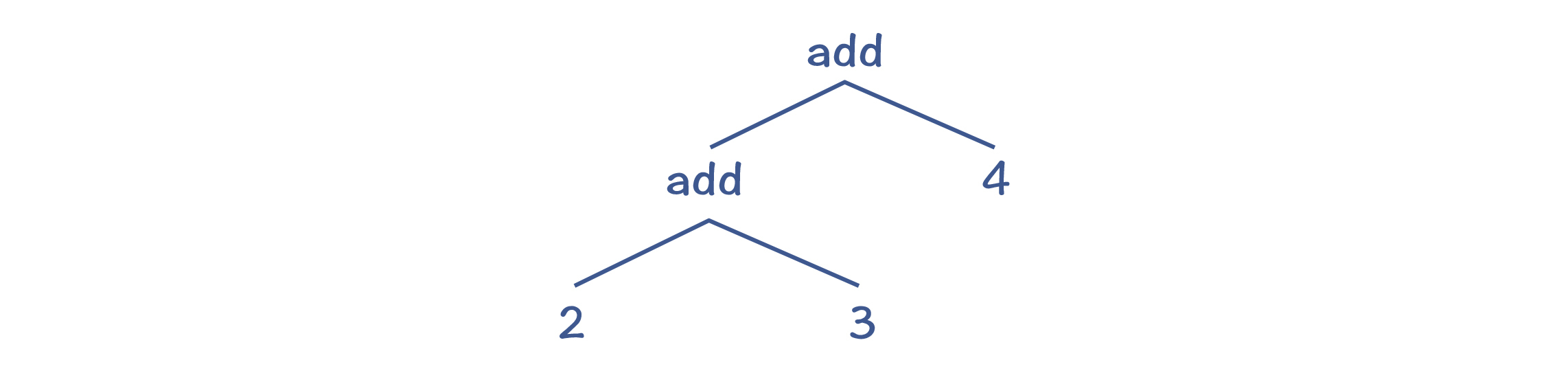
递归下降算法的第二个缺点,就是当产生式匹配失败的时候,必须要“回溯”,这就可能导致浪费。
这个时候,我们有个针对性的解决办法,就是预读后续的一个Token,判断该选择哪个产生式。
以stmt变元为例,考虑它的三个产生式,分别是变量声明语句、表达式语句和return语句。那么在递归下降算法中,我们可以在这里预读一个Token,看看能否根据这个Token来选择某个产生式。
经过仔细观察,你发现如果预读的Token是Int或Long,就选择变量声明语句;如果是IntLiteral、Id或左括号,就选择表达式语句;而如果是Return,则肯定是选择return语句。因为这三个语句开头的Token是不重叠的,所以你可以很明确地做出选择。
如果我们手写递归下降算法,可以用肉眼识别出每次应该基于哪个Token,选择用哪个产生式。但是,对于一些比较复杂的语法规则,我们要去看好几层规则,这样比较辛苦。
那么能否有一个算法,来自动计算出选择不同产生式的依据呢?当然是有的,这就是LL算法家族。
LL算法的要点,就是计算First和Follow集合。
First集合是每个产生式开头可能会出现的Token的集合。就像stmt有三个产生式,它的First集合如下表所示。
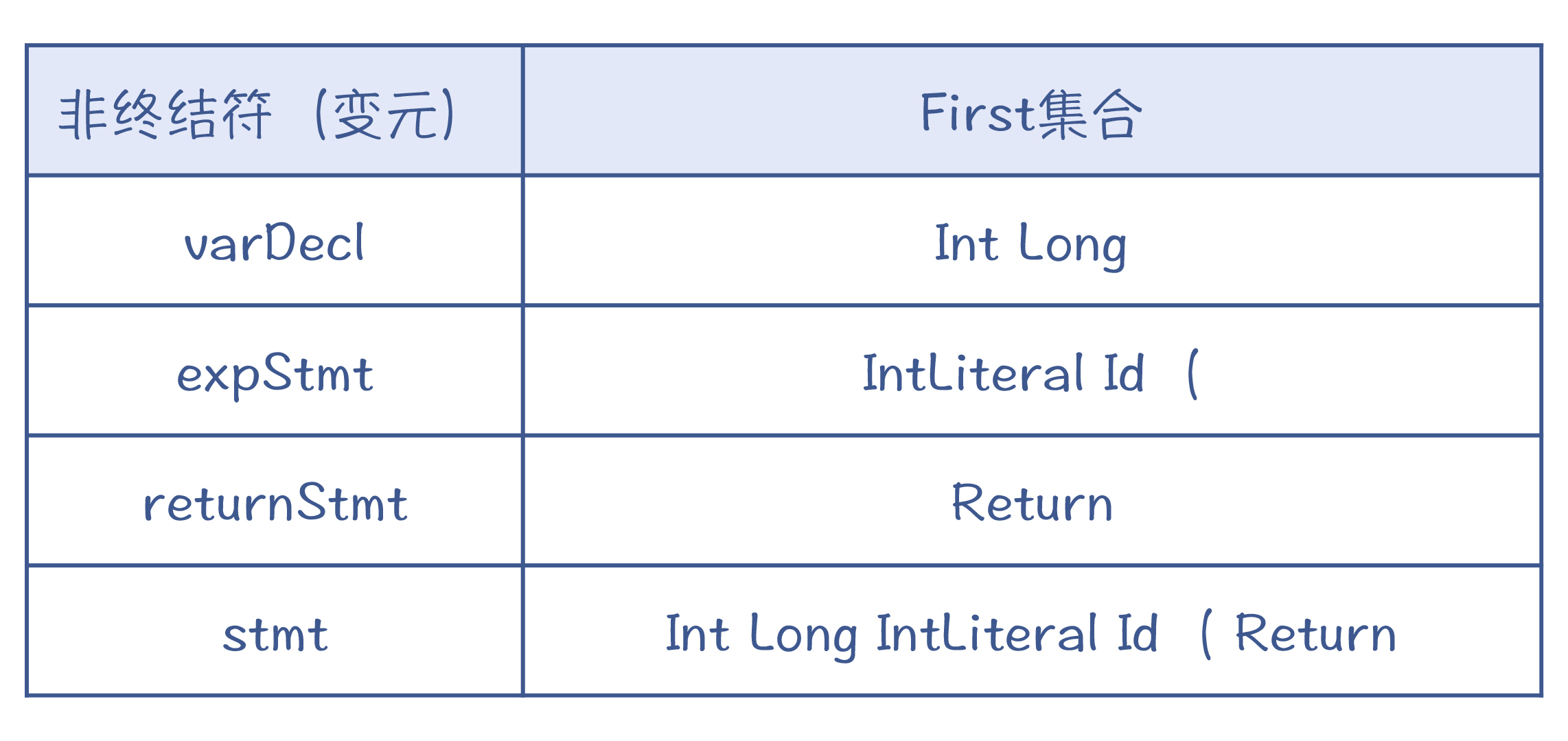
而stmt的First集合,就是三个产生式的First集合的并集,也是Int Long IntLiteral Id ( Return。
总体来说,针对非终结符x,它的First集合的计算规则是这样的:
在计算First集合的时候,具体可以采用“不动点法”。相关细节这里就不展开了,你可以参考示例程序FirstFollowSet类的CalcFirstSets()方法,运行示例程序能打印各个非终结符的First集合。
不过,这样是不是就万事大吉了呢?
其实还有一种特殊情况我们需要考虑,那就是对于某个非终结符,它自身会产生ε的情况。比如说,示例文法中的blockStmts,它是可能产生ε的,也就是块中一个语句都没有。
block : '{' blockStmts '}' ; //语句块
blockStmts : stmt* ; //语句块中的语句
stmt = varDecl | expStmt | returnStmt; //语句
语法解析器在这个时候预读的下一个Token是什么呢?是右花括号。这证明blockStmts产生了ε,所以才读到了后续跟着的花括号。
对于某个非终结符后面可能跟着的Token的集合,我们叫做Follow集合。如果预读到的Token在Follow中,那么我们就可以判断当前正在匹配的这个非终结符,产生了ε。
Follow的算法也比较简单,以非终结符x为例:
这样在计算了First和Follow集合之后,你就可以通过预读一个Token,来完全确定采用哪个产生式。这种算法,就叫做LL(1)算法。
LL(1)中的第一个L,是Left-to-right的缩写,代表从左向右处理Token串。第二个L,是Leftmost的缩写,意思是最左推导。最左推导是什么呢?就是它总是先把产生式中最左侧的非终结符展开完毕以后,再去展开下一个。这也就相当于对AST从左子节点开始的深度优先遍历。LL(1)中的1,指的是预读一个Token。
前面讲的递归下降和LL算法,都是自顶向下的算法。还有一类算法,是自底向上的,其中的代表就是LR算法。
自顶向下的算法,是从根节点逐层往下分解,形成最后的AST;而LR算法的原理呢,则是从底下先拼凑出AST的一些局部拼图,并逐步组装成一棵完整的AST。所以,其中的关键之处在于如何“拼凑”。
假设我们采用下面的上下文无关文法,来推演一个实例,具体语法规则如下所示:
start->add
add->add+mul
add->mul
mul->mul*pri
mul->pri
pri->Int
pri->(add)
如果用于解析“2+3*5”,最终会形成下面的AST:
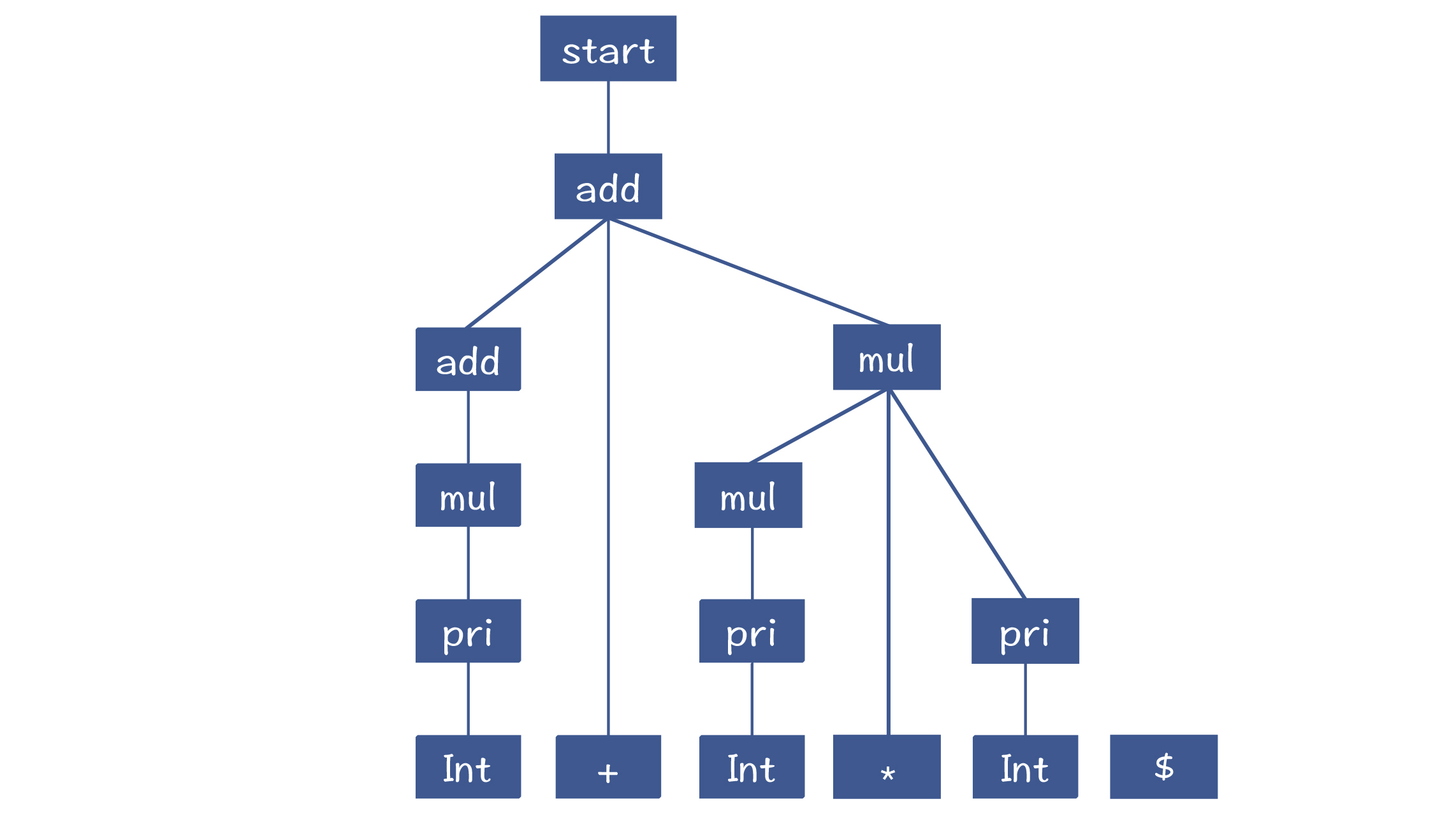
那算法是怎么从底部凑出这棵AST来的呢?
LR算法和LL算法一样,也是从左到右地消化掉Token。在第1步,它会取出“2”这个Token,放到一个栈里,这个栈是用来组装AST的工作区。同时,它还会预读下一个Token,也就是“+”号,用来帮助算法做判断。
在下面的示意图里,我画了一条橙色竖线,竖线的左边是栈,右边是预读到的一个Token。在做语法解析的过程中,竖线会不断地往右移动,把Token放到栈里,这个过程叫做“移进”(Shift)。
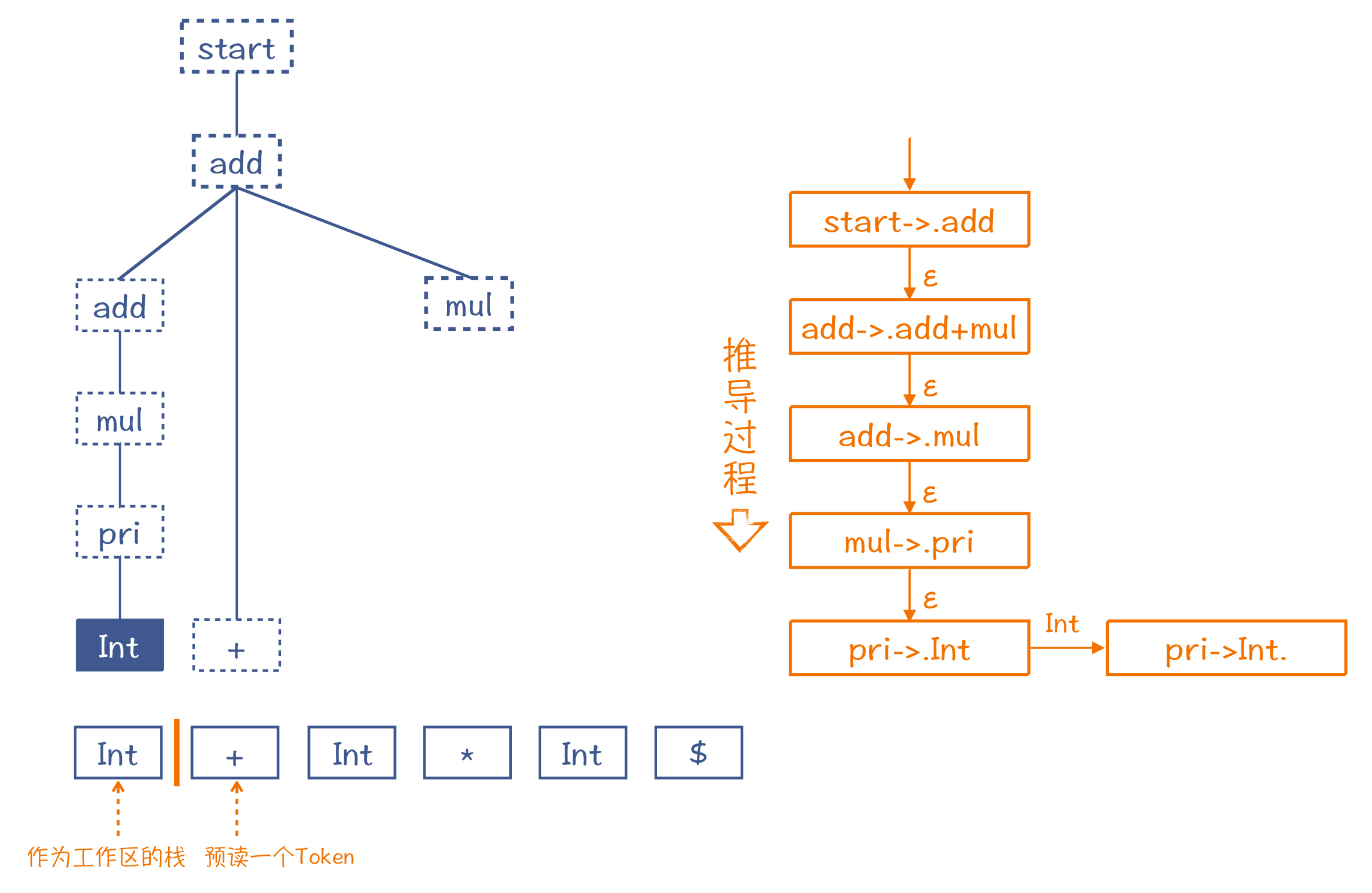
注意,我在图7中还用虚线框推测了AST的其他部分。也就是说,如果第一个Token遇到的是整型字面量,而后面跟着一个+号,那么这两个Token就决定了它们必然是这棵推测出来的AST的一部分。而图中右边就是它的推导过程,其中的每个步骤,都使用了一个产生式加了一个点(如“.add”)。这个点,就相当于图中左边的橙色竖线。
所以你就可以根据这棵假想的AST,也就是依据假想的推导过程,给它反推回去。把Int还原为pri。这个还原过程,就叫做“规约”(Reduce)。工作区里的元素也随之更新成pri。
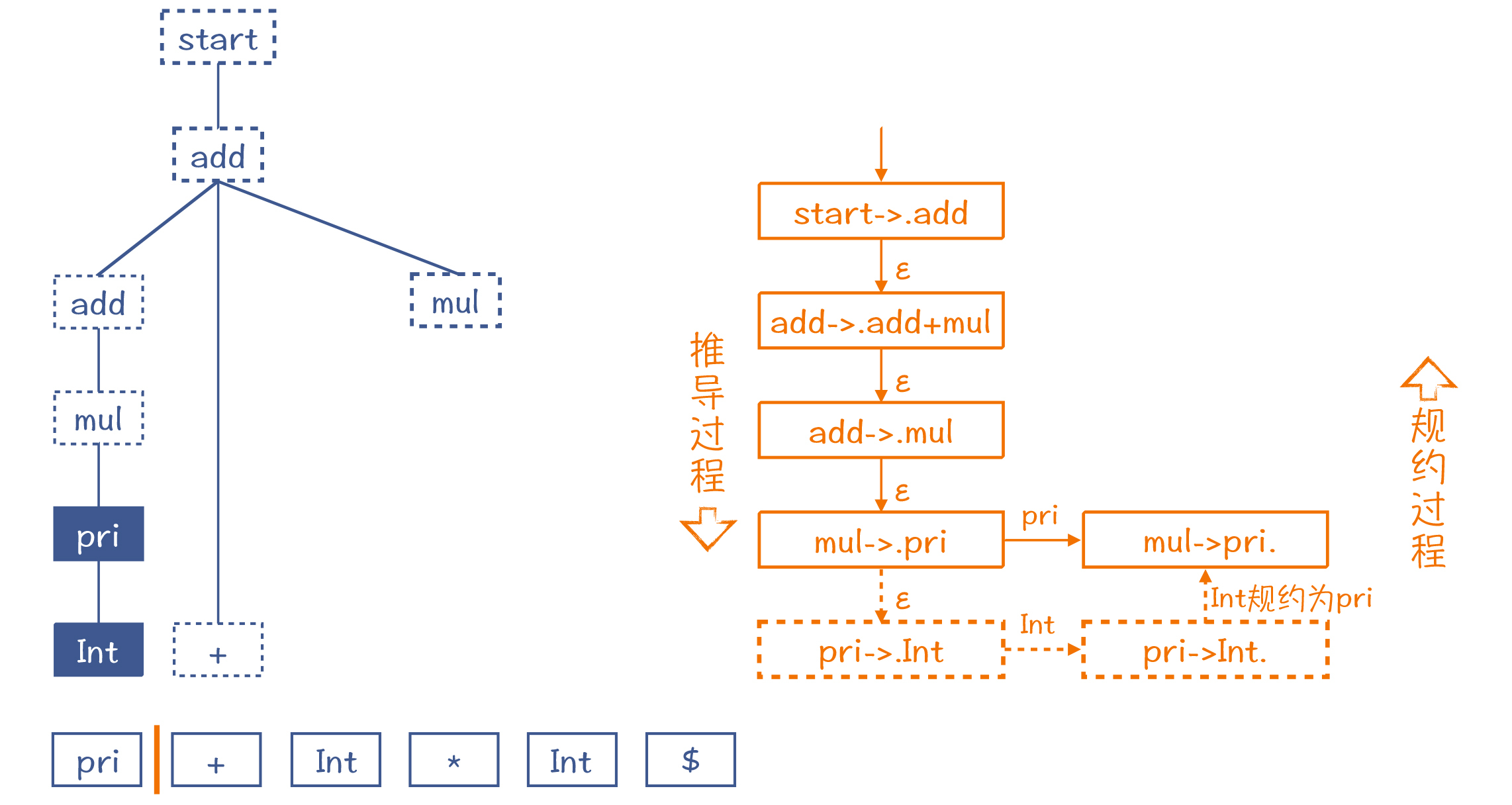
按照这样的思路,不断地移进和规约,这棵AST中推测出来的节点会不断地被证实。而随着读入的Token越来越多,这棵AST也会长得越来越高,整棵树变得更大。下图是推导过程中间的一个步骤。
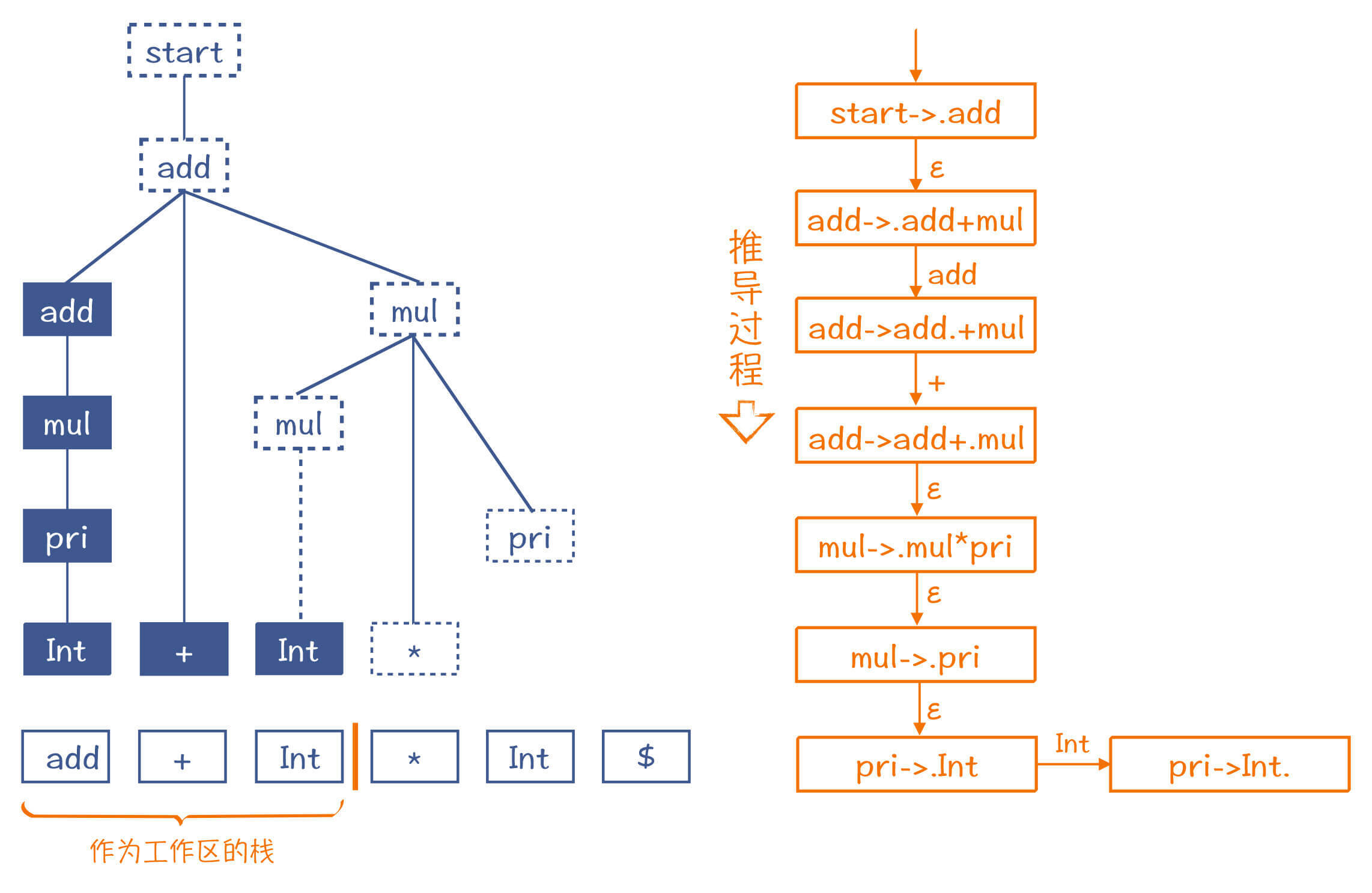
最后,整个AST构造完毕,而工作区里也就只剩了一个Start节点。
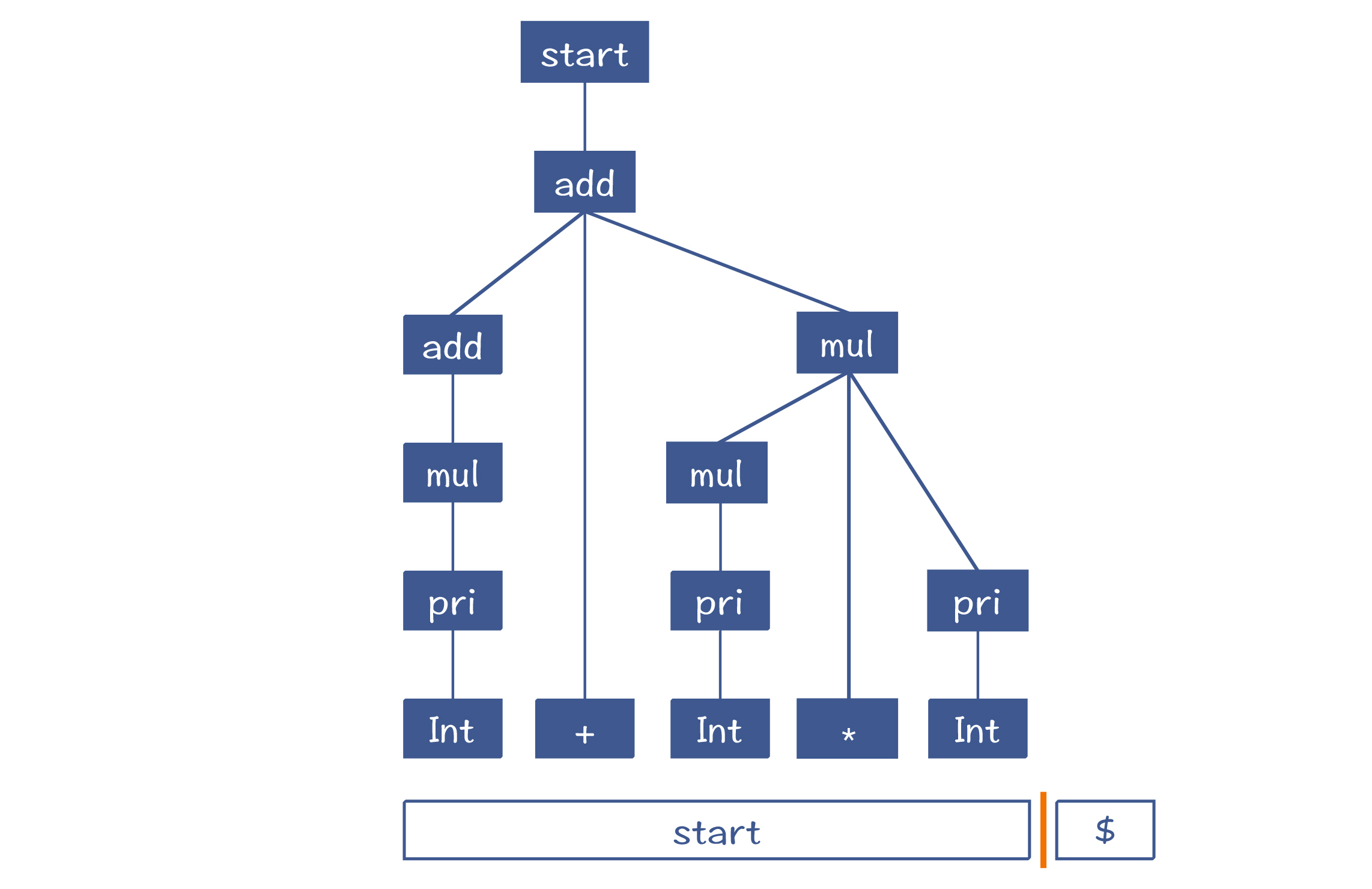
通过上面的介绍,你应该已经建立了对LR算法的直觉认识。如果要把这个推导过程写成严密的算法,你可以参考《编译原理之美》的第18讲。
从示例中,你应该已经看出来了,相对于LL算法,LR算法的优点是能够处理左递归文法。但它也有缺点,比如不利于输出全面的编译错误信息。因为在没有解析完毕之前,算法并不知道最后的AST是什么样子,所以也不清楚当前的语法错误在整体AST中的位置。
最后我再提一下LR的意思,来帮你更完整地理解LR算法。L还是代表从左到右读入Token,而R是最右推导(Rightmost)的意思。我把“2+3*5”最右推导的过程写在了下面,而如果你从最后一行往前一步步地看,它恰好就是规约的过程。

如果你见到LR(k),那它的意思就是会预读k个Token,我们在示例中采用的是LR(1)。
今天花了一讲的时间,把语法分析的要点给你讲解了一下。
对于上下文无关的文法,你要知道产生式、非终结符、终结符、EBNF这几个基本概念,能够熟练阅读各种语言的语法规则,这是一个基本功。
递归下降算法是另一项基本功,所以也一定要掌握。你要注意,递归下降是深度优先的,只有最左边的子树都生成完了,才会往右生成它的兄弟节点。有的同学会在没有把左侧的非终结符匹配完毕的情况下,就开始匹配右边的项,从而不自觉地采用了宽度优先的思路,这是我发现很多同学会容易陷入的一个思维误区。
对于LL算法和LR算法,我只做了简单的讲解,目的是为了帮助你建立直观的理解。我们在后面的课程中,还会遇到使用它们的实际例子,到时你可以与这一讲的内容相互印证。
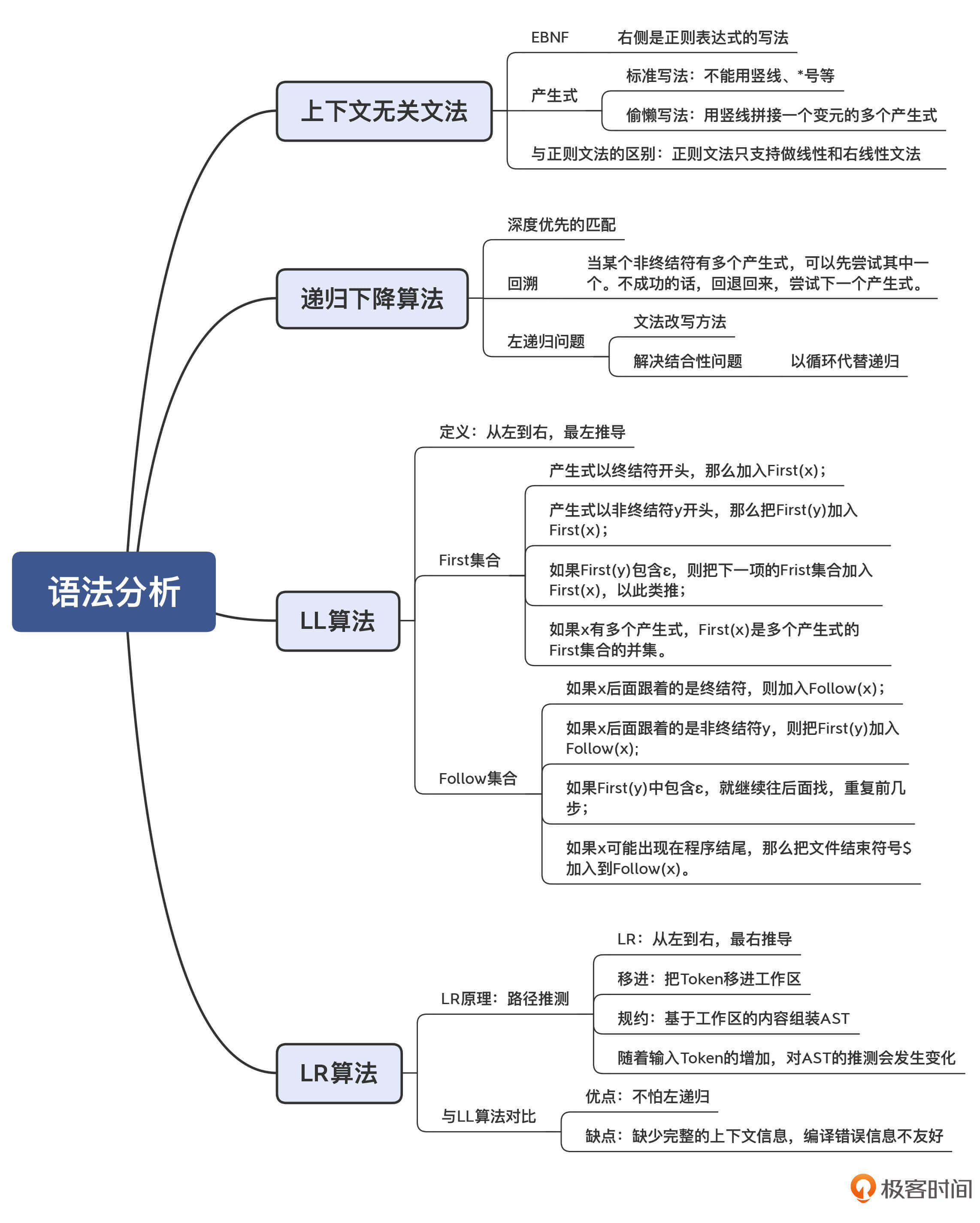
你可以计算一下示例文法中block、blockStmts、stmt、varDecl、returnStmt和expStmt的First和Follow集合吗?这样,你也可以熟悉一下First和Follow集合的计算方法。
欢迎在留言区分享你的答案。如果觉得有收获,也欢迎你把这节课分享给你的朋友。
1.线性文法(Linear Grammar):参见Wikipedia。
2.左递归及其消除方法:参见Wikipedia。
评论