你好,我是月影。
曲线是图形系统的基本元素之一,它可以构成几何图形的边,也可以描述点和几何体的运动轨迹,还可以控制像素属性的变化。不论我们用什么图形系统绘图,图形的呈现都离不开曲线。因此,对于可视化而言,掌握如何描述曲线是非常重要的。
今天,我们就来学习两种常见的描述曲线的方法,也就是用向量和参数方程来描述曲线。
我们先来说第一种方法,用向量来描述曲线。
我们知道,曲线是可以用折线来模拟的。因此,我们第5节课中用向量来绘制折线的方法,同样可以应用于曲线。具体怎么做呢?下面,我就详细来说说。
首先,我们用向量绘制折线的方法来绘制正多边形,我们定义一个函数regularShape,代码如下:
function regularShape(edges = 3, x, y, step) {
const ret = [];
const delta = Math.PI * (1 - (edges - 2) / edges);
let p = new Vector2D(x, y);
const dir = new Vector2D(step, 0);
ret.push(p);
for(let i = 0; i < edges; i++) {
p = p.copy().add(dir.rotate(delta));
ret.push(p);
}
return ret;
}
我们在regularShape函数中,给定边数edges、起点x, y、一条边的长度step,就可以绘制一个正多边形了。绘制的思路和我们上一节课的思路类似,也就是通过rotate旋转向量,然后通过向量加法来计算顶点位置。
具体来说就是,我们定义初始点为new Vector2D(x, y),初始方向为x轴方向new Vector2D(step, 0)。然后循环计算正多边形的顶点位置,也就是从初始点开始,每次将方向向量旋转delta角度,delta角度是根据正多边形内角公式计算出来的。最后,我们将当前点和方向向量相加,就得到下一个顶点坐标了。
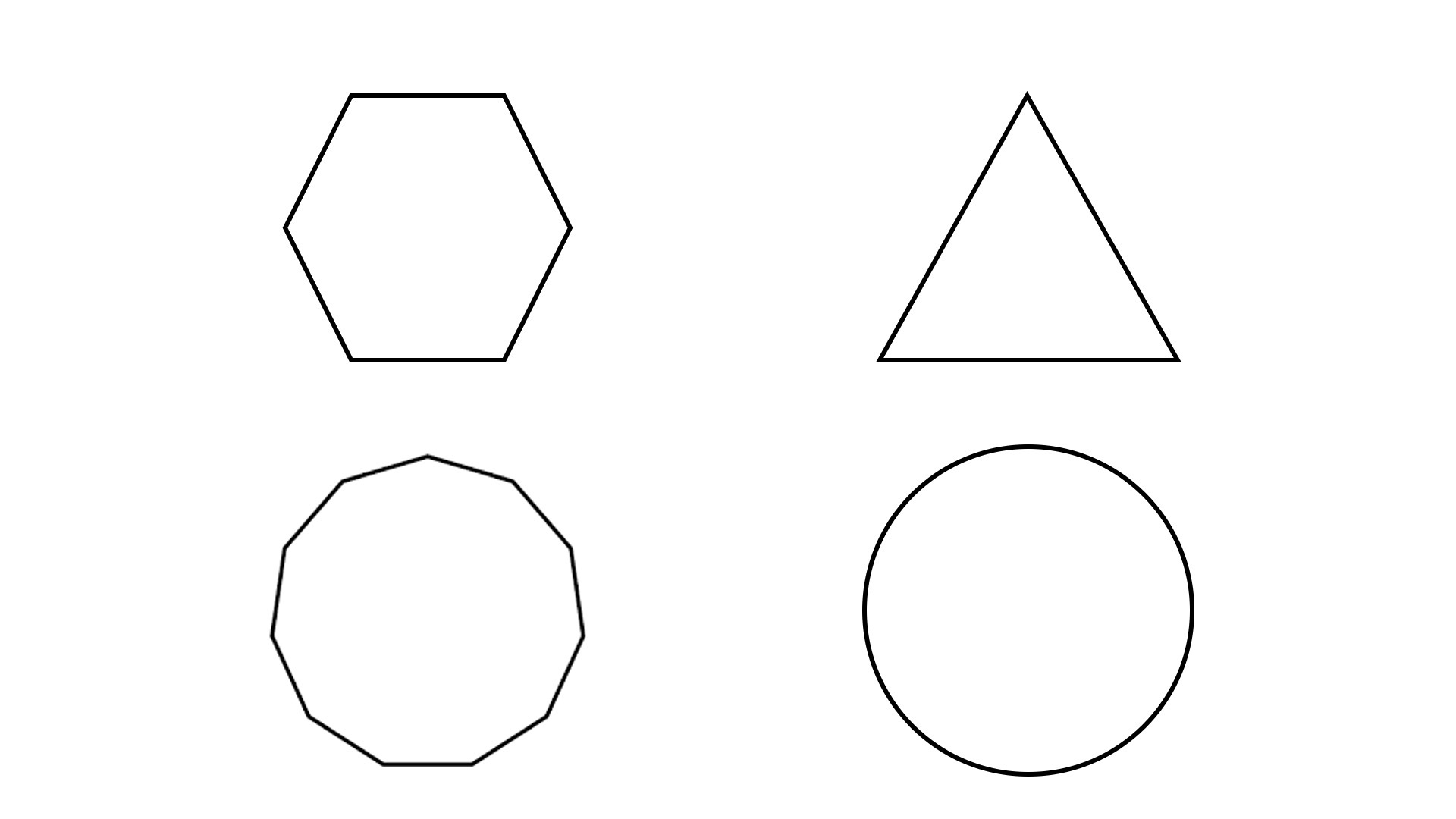
有了这个方法,我们就可以计算出要绘制的多边形的每一个顶点坐标,然后调用图形系统的API将图形绘制出来了。我在下面给出了绘制三角形、六边形、十一边形和六十边形的参数,你可以看一看,也可以试着自己动手绘制一下。
draw(regularShape(3, 128, 128, 100)); // 绘制三角形
draw(regularShape(6, -64, 128, 50)); // 绘制六边形
draw(regularShape(11, -64, -64, 30)); // 绘制十一边形
draw(regularShape(60, 128, -64, 6)); // 绘制六十边形
这些图形用Canvas2D绘制出来的结果如下图所示,详细的代码我放在了GitHub仓库。

从上面的例子中可以看出,当多边形的边数非常多的时候,这个图形就会接近圆。所以,只要利用regularShape函数,将多边形的边数设置得很大,我们就可以绘制出圆形了。不过,这个做法虽然能够绘制出圆这样的曲线,但它还有一些缺点。
首先,regularShape定义边数、起点、一条边的长度,这就和我们通常的使用习惯,也就是定义边数、中心和半径不符。如果我们按照现在这种定义方式绘图,是很难精确对应到图形的位置和大小的。那你可能要说了,不是还可以换算吗?确实可以,但是计算的过程比较繁琐,也很容易出错。
其次,regularShape可以画圆,改进一下也可以画圆弧,但是对于椭圆、抛物线、贝塞尔曲线等其他曲线的绘制就无能为力了。
那么,为了更简单地绘制出更多的曲线样式,我们需要用更好的模型来描述。
接下来,我们就来讨论用参数方程描述曲线的方法。通过这个方法,我们不仅可以描述常见的圆、椭圆、抛物线、正余弦等曲线,还能描述更具有一般性的曲线,也就是没有被数学公式预设好的曲线,比如贝塞尔曲线,或者Catmull–Rom曲线等等。
说到参数方程,接下来我在每次用它来画图之前,还是会先带你一起回顾相关的数学知识,这样对你后面的学习也会很方便。那我们先从最简单的曲线,也就是圆形开始,来看看它是如何用参数方程绘制的。
首先,圆可以用一组参数方程来定义。如下所示的参数方程,定义了一个圆心在(x0,y0),半径为r的圆。
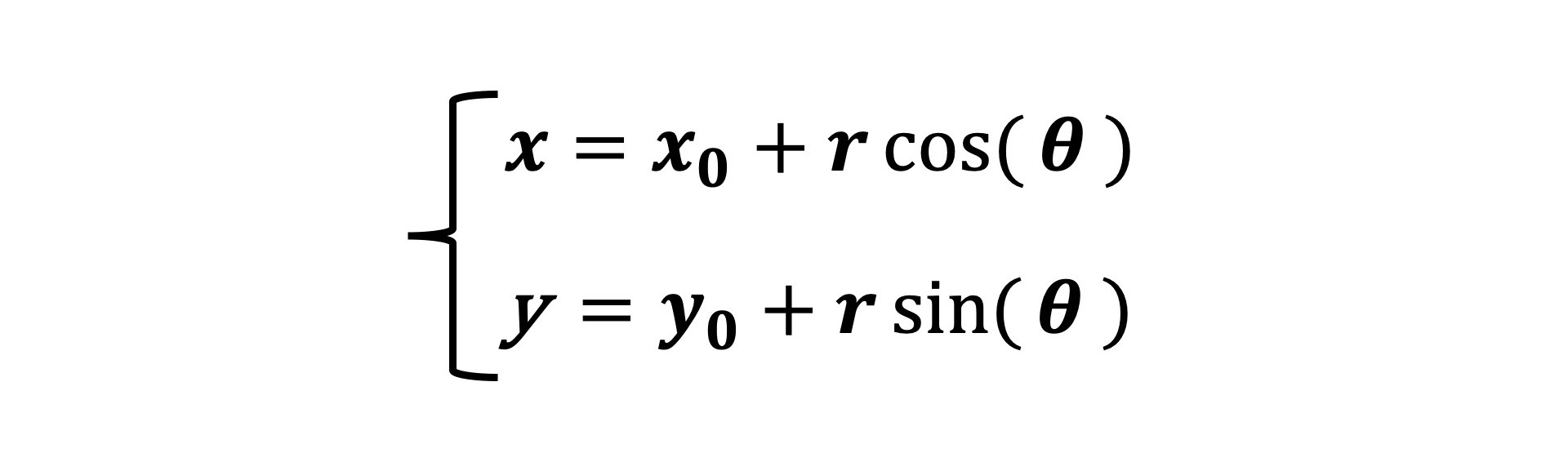
知道了方程,下面我们来说一下计算圆顶点的方法。首先,我们实现一个画圆弧的函数arc,代码如下所示。我们设置圆心为x0、y0,半径为radius,起始角度为startAng,结束角度是endAng。然后,我们就可以用draw(arc(0, 0, 100))这样的方式在(0,0)点绘制一个半径为100的圆了。
const TAU_SEGMENTS = 60;
const TAU = Math.PI * 2;
function arc(x0, y0, radius, startAng = 0, endAng = Math.PI * 2) {
const ang = Math.min(TAU, endAng - startAng);
const ret = ang === TAU ? [] : [[x0, y0]];
const segments = Math.round(TAU_SEGMENTS * ang / TAU);
for(let i = 0; i <= segments; i++) {
const x = x0 + radius * Math.cos(startAng + ang * i / segments);
const y = y0 + radius * Math.sin(startAng + ang * i / segments);
ret.push([x, y]);
}
return ret;
}
draw(arc(0, 0, 100));
这个时候你可能想问,在第2节课利用Canvas2D画圆的时候,我们使用的context.arc方法和我们自己实现的这个函数很像,既然已经有了现成的API,我们为什么还要自己实现呢?关于这一点,我就要再啰嗦几句了。不是所有的图形系统都提供了画圆的API,比如WebGL中就没有默认的画圆API。因此,在没有提供画圆的API的时候,我们上面实现的函数就可以派上用场了。
除了画圆,参数方程还可以描述很多其他的圆锥曲线。比如椭圆的参数方程。它其实和圆的参数方程很接近。其中,a、b分别是椭圆的长轴和短轴,当a = b = r时,这个方程是就圆的方程式。所以,圆实际上就是椭圆的特例。
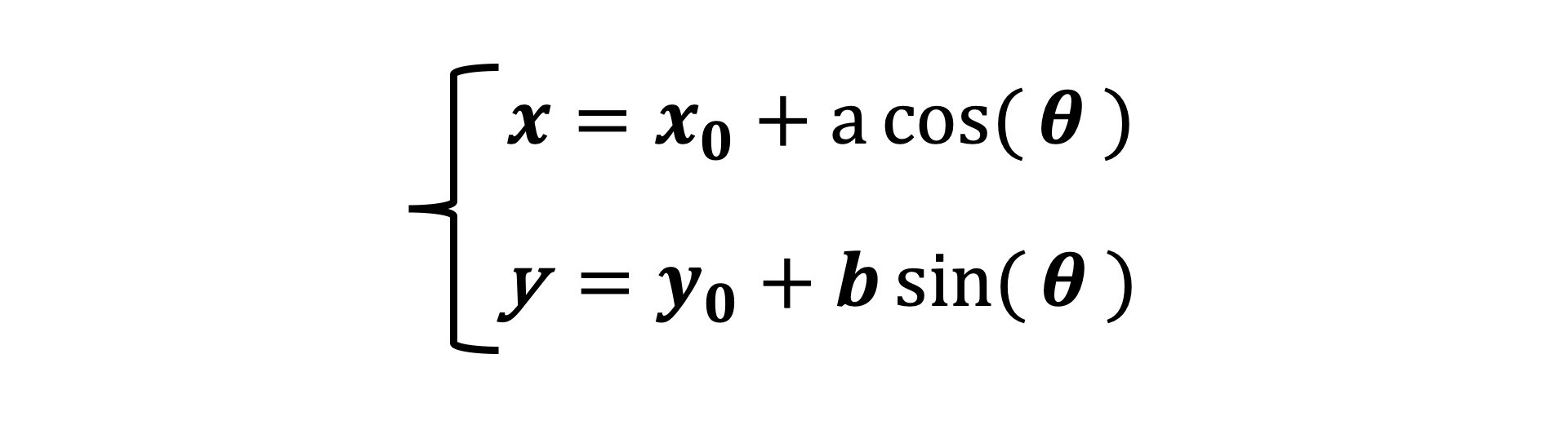
再比如,抛物线的参数方程。其中p是常数,为焦点到准线的距离。
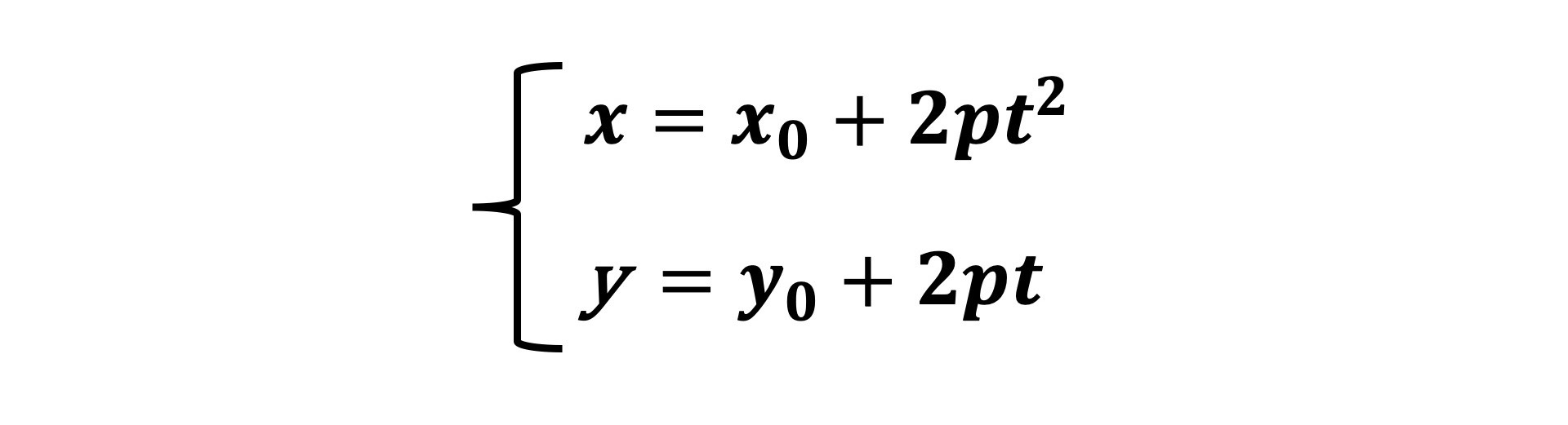
我们修改上面的arc方法中的对应参数,就能同样实现椭圆和抛物线的绘制了。修改的操作非常简单,我就在下面直接给出这两个函数的代码了。
首先是椭圆,它的函数代码如下所示。
const TAU_SEGMENTS = 60;
const TAU = Math.PI * 2;
function ellipse(x0, y0, radiusX, radiusY, startAng = 0, endAng = Math.PI * 2) {
const ang = Math.min(TAU, endAng - startAng);
const ret = ang === TAU ? [] : [[x0, y0]];
const segments = Math.round(TAU_SEGMENTS * ang / TAU);
for(let i = 0; i <= segments; i++) {
const x = x0 + radiusX * Math.cos(startAng + ang * i / segments);
const y = y0 + radiusY * Math.sin(startAng + ang * i / segments);
ret.push([x, y]);
}
return ret;
}
draw(ellipse(0, 0, 100, 50));
其次是抛物线,它的函数代码如下所示。
const LINE_SEGMENTS = 60;
function parabola(x0, y0, p, min, max) {
const ret = [];
for(let i = 0; i <= LINE_SEGMENTS; i++) {
const s = i / 60;
const t = min * (1 - s) + max * s;
const x = x0 + 2 * p * t ** 2;
const y = y0 + 2 * p * t;
ret.push([x, y]);
}
return ret;
}
draw(parabola(0, 0, 5.5, -10, 10));
除了前面说的圆锥曲线,应用参数方程我们还可以绘制许多比较有趣的曲线,这些曲线在实际工作中,常常用来构建各种几何图形。
不过,如果我们为每一种曲线都分别对应实现一个函数,就会非常笨拙和繁琐。那为了方便,我们可以用函数式的编程思想,封装一个更简单的JavaScript参数方程绘图模块,以此来绘制出不同的曲线。这个绘图模块的使用过程主要分为三步。
第一步,我们实现一个叫做parametric的高阶函数,它的参数分别是x、y坐标和参数方程。
第二步,parametric会返回一个函数,这个函数会接受几个参数,比如,start、end这样表示参数方程中关键参数范围的参数,以及seg这样表示采样点个数的参数等等。在下面的代码中,当seg默认100时,就表示在start、end范围内采样101(seg+1)个点,后续其他参数是作为常数传给参数方程的数据。
第三步,我们调用parametric返回的函数之后,它会返回一个对象。这个对象有两个属性:一个是points,也就是它生成的顶点数据;另一个是draw方法,我们可以利用这个draw方法完成绘图。
这个过程的代码如下:
// 根据点来绘制图形
function draw(points, context, {
strokeStyle = 'black',
fillStyle = null,
close = false,
} = {}) {
context.strokeStyle = strokeStyle;
context.beginPath();
context.moveTo(...points[0]);
for(let i = 1; i < points.length; i++) {
context.lineTo(...points[i]);
}
if(close) context.closePath();
if(fillStyle) {
context.fillStyle = fillStyle;
context.fill();
}
context.stroke();
}
export function parametric(xFunc, yFunc) {
return function (start, end, seg = 100, ...args) {
const points = [];
for(let i = 0; i <= seg; i++) {
const p = i / seg;
const t = start * (1 - p) + end * p;
const x = xFunc(t, ...args); // 计算参数方程组的x
const y = yFunc(t, ...args); // 计算参数方程组的y
points.push([x, y]);
}
return {
draw: draw.bind(null, points),
points,
};
};
}
利用绘图模块,我们就可以绘制出各种有趣的曲线了。比如,我们可以很方便地绘制出抛物线,代码如下:
// 抛物线参数方程
const para = parametric(
t => 25 * t,
t => 25 * t ** 2,
);
// 绘制抛物线
para(-5.5, 5.5).draw(ctx);
再比如,我们可以绘制出阿基米德螺旋线,代码如下:
const helical = parametric(
(t, l) => l * t * Math.cos(t),
(t, l) => l * t * Math.sin(t),
);
helical(0, 50, 500, 5).draw(ctx, {strokeStyle: 'blue'});
以及,我们还可以绘制星形线,代码如下:
const star = parametric(
(t, l) => l * Math.cos(t) ** 3,
(t, l) => l * Math.sin(t) ** 3,
);
star(0, Math.PI * 2, 50, 150).draw(ctx, {strokeStyle: 'red'});
同时绘制三条曲线后的效果,如下图所示。详细的代码,我都放到了GitHub仓库。你可以自己动手试一试,看看怎么把它们组合成更多有趣的图形。
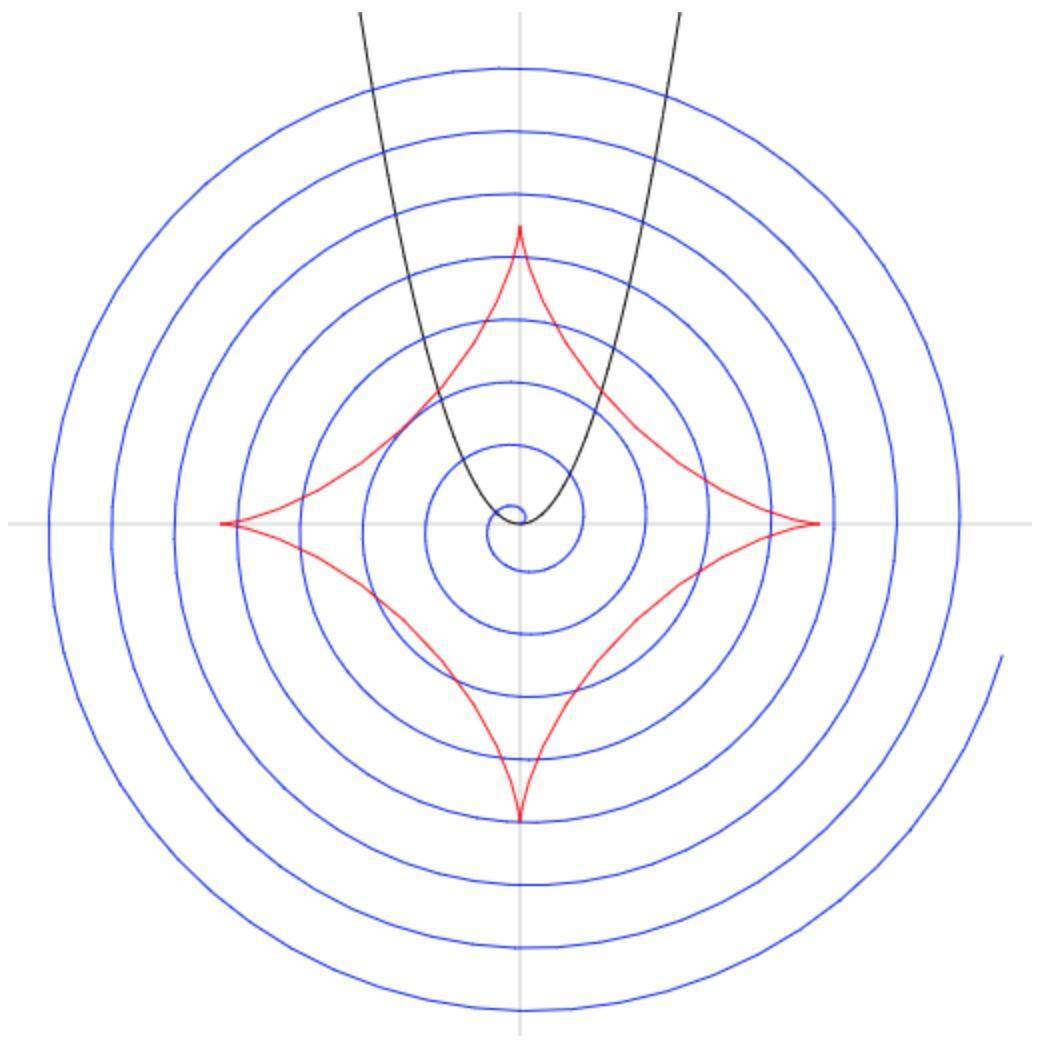
前面我们说的这些曲线都比较常见,它们都是符合某种固定数学规律的曲线。但生活中还有很多不规则的图形,无法用上面这些规律的曲线去描述。那我们该如何去描述这些不规则图形呢?贝塞尔曲线(Bezier Curves)就是最常见的一种解决方式。它在可视化领域中也是一类非常常用的曲线,它通过起点、终点和少量控制点,就能定义参数方程来生成复杂的平滑曲线,所以它通常被用来构建数据信息之间连接线。
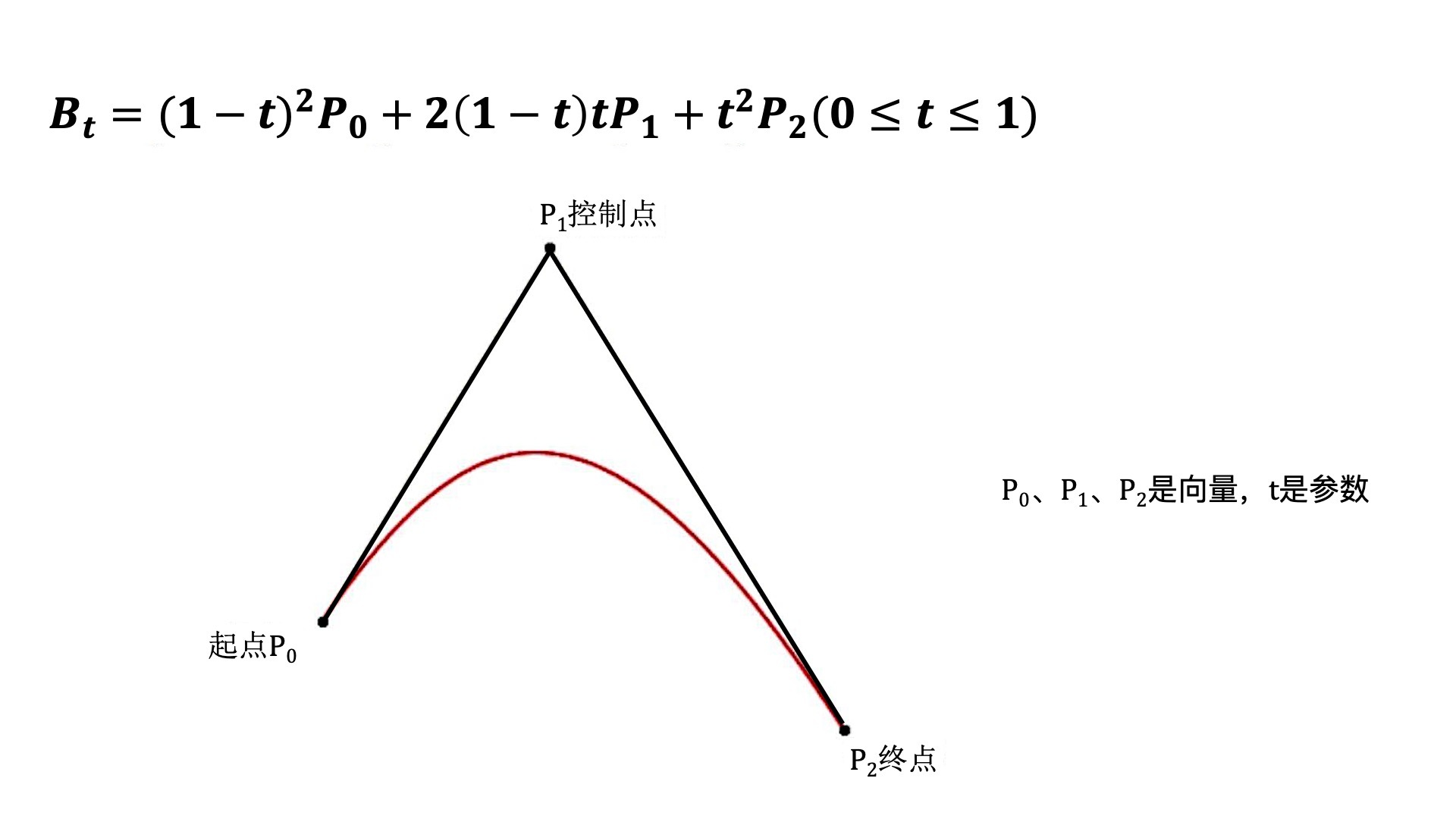
贝塞尔曲线又分为二阶贝塞尔曲线(Quadratic Bezier Curve)和三阶贝塞尔曲线(Qubic Bezier Curve)。顾名思义,二阶贝塞尔曲线的参数方程是一元二次多项式,那么三阶贝塞尔曲线的参数方程是一元三次多项式。接下来,我们就分别说说它们的公式和描述曲线的方法
其中,二阶贝塞尔曲线由三个点确定,P0是起点,P1是控制点,P2是终点,示意图如下:
我们可以用parametric构建并绘制二阶贝塞尔曲线,代码如下所示:
const quadricBezier = parametric(
(t, [{x: x0}, {x: x1}, {x: x2}]) => (1 - t) ** 2 * x0 + 2 * t * (1 - t) * x1 + t ** 2 * x2,
(t, [{y: y0}, {y: y1}, {y: y2}]) => (1 - t) ** 2 * y0 + 2 * t * (1 - t) * y1 + t ** 2 * y2,
);
const p0 = new Vector2D(0, 0);
const p1 = new Vector2D(100, 0);
p1.rotate(0.75);
const p2 = new Vector2D(200, 0);
const count = 30;
for(let i = 0; i < count; i++) {
// 绘制30条从圆心出发,旋转不同角度的二阶贝塞尔曲线
p1.rotate(2 / count * Math.PI);
p2.rotate(2 / count * Math.PI);
quadricBezier(0, 1, 100, [
p0,
p1,
p2,
]).draw(ctx);
}
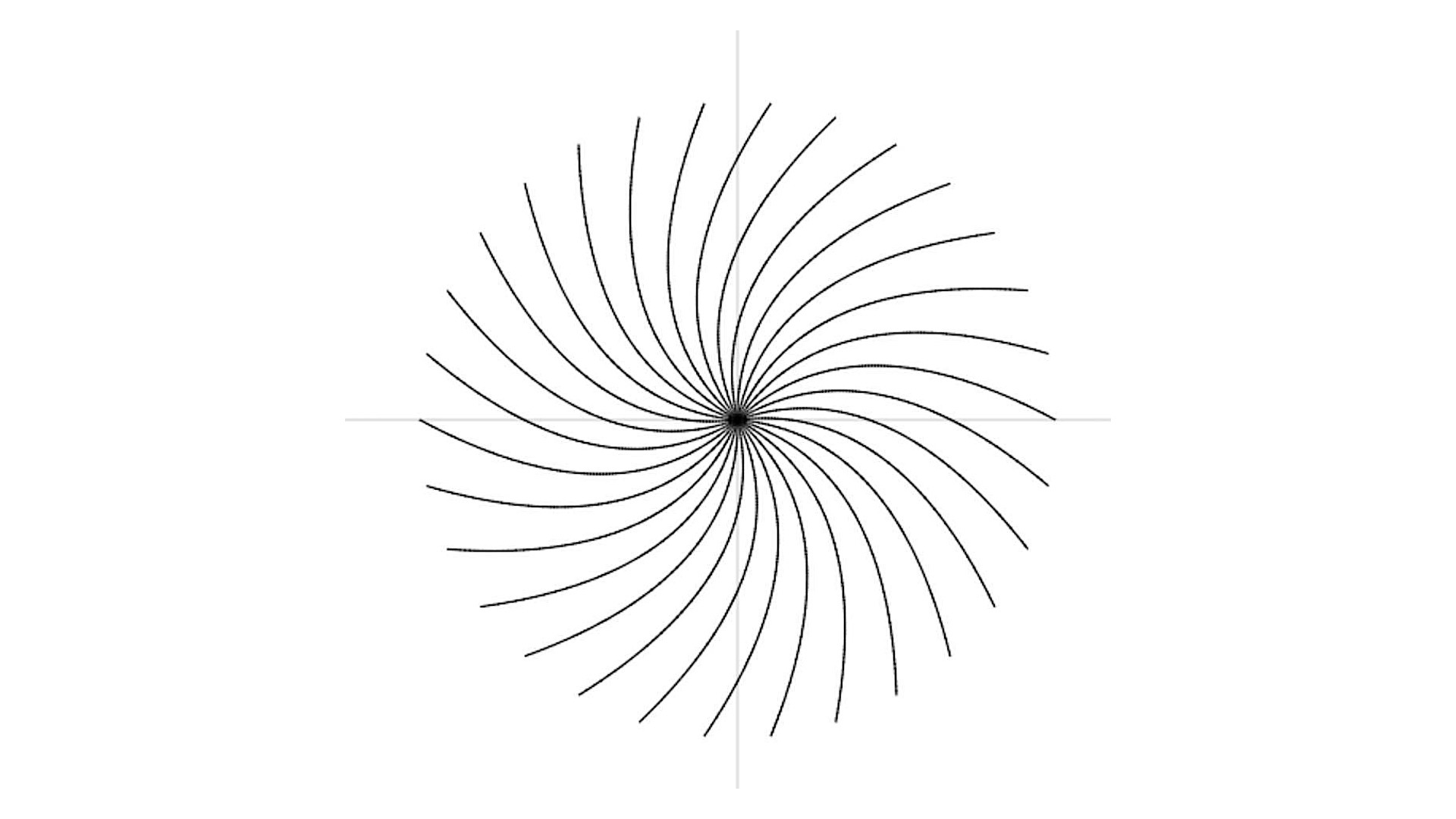
在上面的代码中,我们绘制了30个二阶贝塞尔曲线,它们的起点都是(0,0),终点均匀分布在半径200的圆上,控制点均匀地分布在半径100的圆上。最终,实现的效果如下图所示。详细的代码,你可以访问GitHub仓库:
三阶贝塞尔曲线的参数方程为:

可以看到,与二阶贝塞尔曲线相比,三阶贝塞尔曲线有4个点,其中P0和P3是起点和终点,P1、P2是控制点,所以三阶贝塞尔曲线有两个控制点。
我们同样可以用parametric构建并绘制三阶贝塞尔曲线:
const cubicBezier = parametric(
(t, [{x: x0}, {x: x1}, {x: x2}, {x: x3}]) => (1 - t) ** 3 * x0 + 3 * t * (1 - t) ** 2 * x1 + 3 * (1 - t) * t ** 2 * x2 + t ** 3 * x3,
(t, [{y: y0}, {y: y1}, {y: y2}, {y: y3}]) => (1 - t) ** 3 * y0 + 3 * t * (1 - t) ** 2 * y1 + 3 * (1 - t) * t ** 2 * y2 + t ** 3 * y3,
);
const p0 = new Vector2D(0, 0);
const p1 = new Vector2D(100, 0);
p1.rotate(0.75);
const p2 = new Vector2D(150, 0);
p2.rotate(-0.75);
const p3 = new Vector2D(200, 0);
const count = 30;
for(let i = 0; i < count; i++) {
p1.rotate(2 / count * Math.PI);
p2.rotate(2 / count * Math.PI);
p3.rotate(2 / count * Math.PI);
cubicBezier(0, 1, 100, [
p0,
p1,
p2,
p3,
]).draw(ctx);
}
三阶贝塞尔曲线控制点比二阶贝塞尔曲线多,这有什么优势呢?因为控制点越多,曲线能够模拟出更多不同的形状,也能更精确地控制细节。比如说,在上面的代码中,我们绘制了30个三阶贝塞尔曲线,它们的起点都为(0,0),终点均匀分布在半径200的圆上,控制点1均匀分布在半径为100的圆上,控制点2均匀分布半径150的圆上。它和我们之前实现的二阶贝塞尔曲线相比,控制得更细致,形成的图案信息更丰富。

总的来说,贝塞尔曲线对于可视化,甚至整个计算机图形学都有着极其重要的意义。因为它能够针对一组确定的点,在其中构造平滑的曲线,这也让图形的实现有了更多的可能性。而且,贝塞尔曲线还可以用来构建Catmull–Rom曲线。Catmull–Rom曲线也是一种常用的曲线,它可以平滑折线,我们在数据统计图表中经常会用到它。

实际上Canvas2D和SVG都提供了直接绘制贝塞尔曲线的API,比如在Canvas2D中,我们可以通过创建Path2D对象,使用Path2D支持的SVGPath指令添加贝塞尔曲线。即使如此,我们依然需要掌握贝塞尔曲线的基本原理。因为在WebGL这样的图形系统里,我们还是需要自己实现贝塞尔曲线的绘制,而且贝塞尔曲线除了绘制曲线之外,还有其他的用处,比如构建平滑的轨迹动画、属性插值等等。这些内容,我们也会在后续课程中会深入讨论。
这一节课我们讨论了用曲线和参数方程描述曲线的方法。
用向量描述比较简单直接,先确定起始点和起始向量,然后通过旋转和向量加法来控制形状,就可以将曲线一段一段地绘制出来。但是它的缺点也很明显,就是数学上不太直观,需要复杂的换算才能精确确定图形的位置和大小。
使用参数方程能够避免向量绘制的缺点,因此是更常用的绘制方式。使用参数方程绘制曲线时,我们既可以使用有规律的曲线参数方程来绘制这些规则曲线,还可以使用二阶、三阶贝塞尔曲线来在起点和终点之间构造平滑曲线。
欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课见!
[1]绘制圆锥曲线完整代码.
[2]绘制其他曲线完整代码.
[3]绘制贝塞尔曲线完整代码.
评论