你好，我是月影。

在前面的课程里，我们学习过使用仿射变换来移动和旋转二维图形。那在三维世界中，想要移动和旋转物体，我们也需要使用仿射变换。

但是，仿射变换该怎么从二维扩展到三维几何空间呢？今天，我们就来看一下三维仿射变换的基本方法，以及怎么对它进行优化。

三维仿射变换和二维仿射变换类似，也包括平移、旋转与缩放等等，而且具体的变换公式也相似。

比如，对于平移变换来说，如果向量$P(x_{0},y_{0},z_{0})$沿着向量 $Q(x_{1},y_{1},z_{1})$平移，我们只需要让$P$加上$Q$，就能得到变换后的坐标。

$$
\left\{\begin{array}{l}
x=x_{0}+x_{1} \\\
y=y_{0}+y_{1} \\\
z=z_{0}+z_{1}
\end{array}\right.
$$

再比如，对于缩放变换来说，我们直接让三维向量乘上标量，就相当于乘上要缩放的倍数就可以了。最后我们得到的三维缩放变换矩阵如下：

$$
M=\left[\begin{array}{ccc}
s_{x} & 0 & 0 \\\
0 & s_{y} & 0 \\\
0 & 0 & s_{z}
\end{array}\right]
$$

而且，我们也可以使用齐次矩阵来表示三维仿射变换，通过引入一个新的维度，就可以把仿射变换转换为齐次矩阵的线性变换了。

$$
M’=\left[\begin{array}{ccc}
M & 0 \\\
0 & 1
\end{array}\right]
$$

这个齐次矩阵，是一个4X4的矩阵，其实它就是我们在第20节课提到的模型矩阵（ModelMatrix）。

总之，对于三维的仿射变换来说，平移和缩放都只是增加一个$z$分量，这和二维放射变换没有什么不同。但对于物体的旋转变换，三维就要比二维稍微复杂一些了。因为二维旋转只有一个参考轴，就是$z$轴，所以二维图形旋转都是围绕着$z$轴的。但是，三维物体的旋转却可以围绕$x、y、z$，这三个轴其中任意一个轴来旋转。

因此，这节课，我们就把重点放在处理三维物体的旋转变换上。

使用欧拉角来旋转几何体

我们先来看一下三维物体的旋转变换矩阵：

$$绕y轴旋转：R_{y}=\left[\begin{array}{ccc}\cos \alpha & 0 & \sin \alpha \\\ 0 & 1 & 0 \\\ -\sin \alpha & 0 & \cos \alpha\end{array}\right]$$

$$绕x轴旋转：R_{x}=\left[\begin{array}{ccc}1 & 0 & 0 \\\ 0 & \cos \beta & -\sin \beta \\\ 0 & \sin \beta & \cos \beta\end{array}\right]$$

$$绕z轴旋转：R_{z}=\left[\begin{array}{ccc}\cos \gamma & -\sin \gamma & 0 \\\ \sin \gamma & \cos \gamma & 0 \\\ 0 & 0 & 1\end{array}\right]$$

你会看到，我们使用了三个旋转矩阵$Ry、Rx、Rz$来描述三维的旋转变换。这三个旋转矩阵分别表示几何体绕$y$轴、$x$轴、$z$轴转过$α、β、γ$角。而这三个角，就叫做欧拉角。

什么是欧拉角？

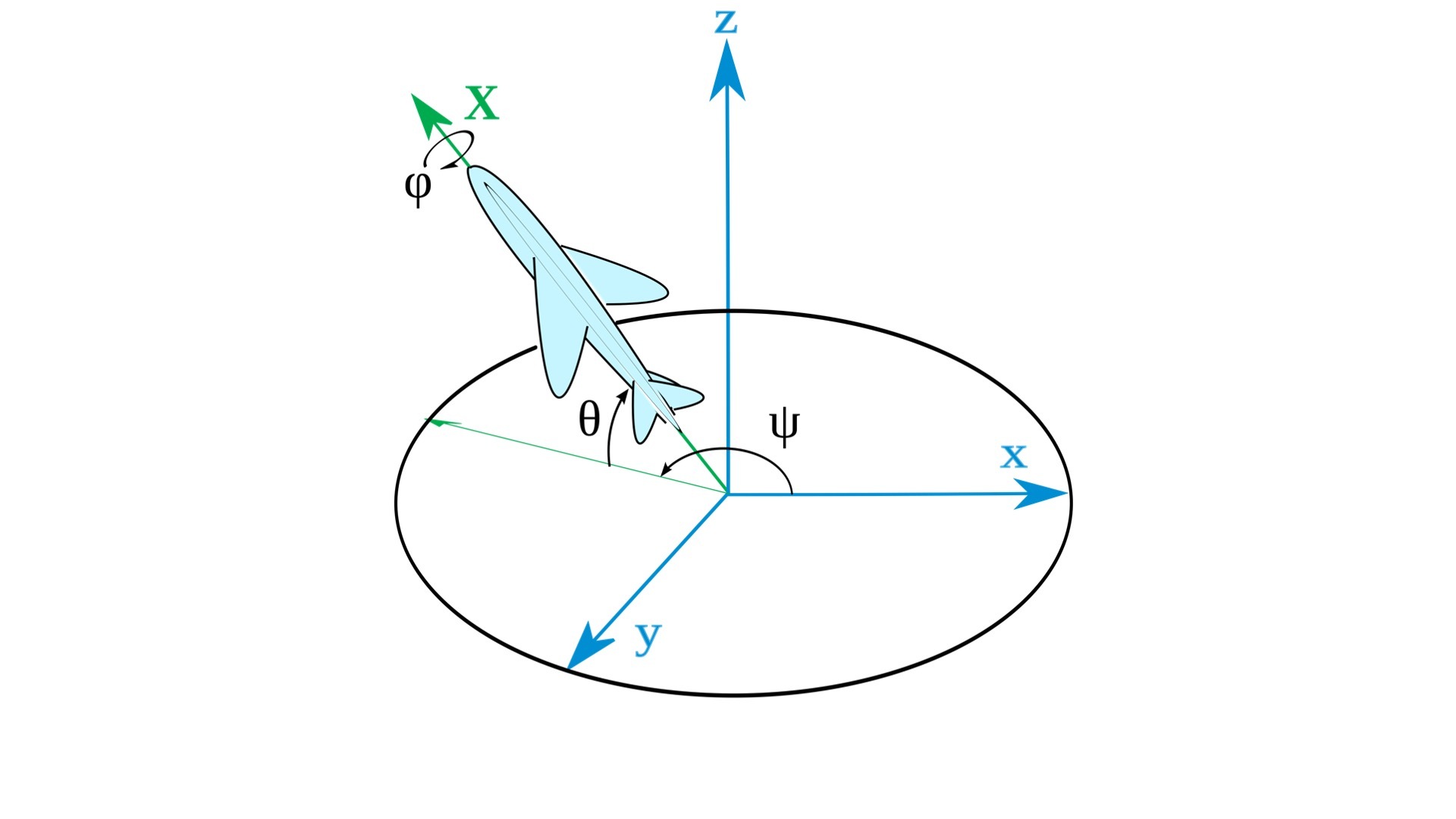
那什么是欧拉角呢？欧拉角是描述三维物体在空间中取向的标准数学模型，也是航空航天普遍采用的标准。对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表示。

举个例子，下图中这个飞机的飞行姿态，可以由绕$x$轴的旋转角度（翻滚机身）、绕$y$轴的旋转角度（俯仰），以及绕$z$轴的旋转角度（偏航）来表示。

也就是说，这个飞机的姿态可以由这三个欧拉角来确定。具体的表示公式就是$Rx、Ry、Rz$，这三个旋转矩阵相乘。

$$M=R_{y} \times R_{x} \times R_{z}$$

这里，我们是按照$Ry、Rx、Rz$的顺序相乘的。而$y-x-z$顺序有一个专属的名字叫做欧拉角的顺规，也就是说，我们现在采用的是$y-x-z$顺规。欧拉角有很多种不同的顺规表示方式，一共可以分两种：一种叫做Proper Euler angles，包含六种顺规，分别是$z-x-z、x-y-x、y-z-y、z-y-z、x-z-x、y-x-y$；另一种叫做Tait–Bryan angles，也包含六种顺规，分别是$x-y-z、y-z-x、z-x-y、x-z-y、z-y-x、 y-x-z$。

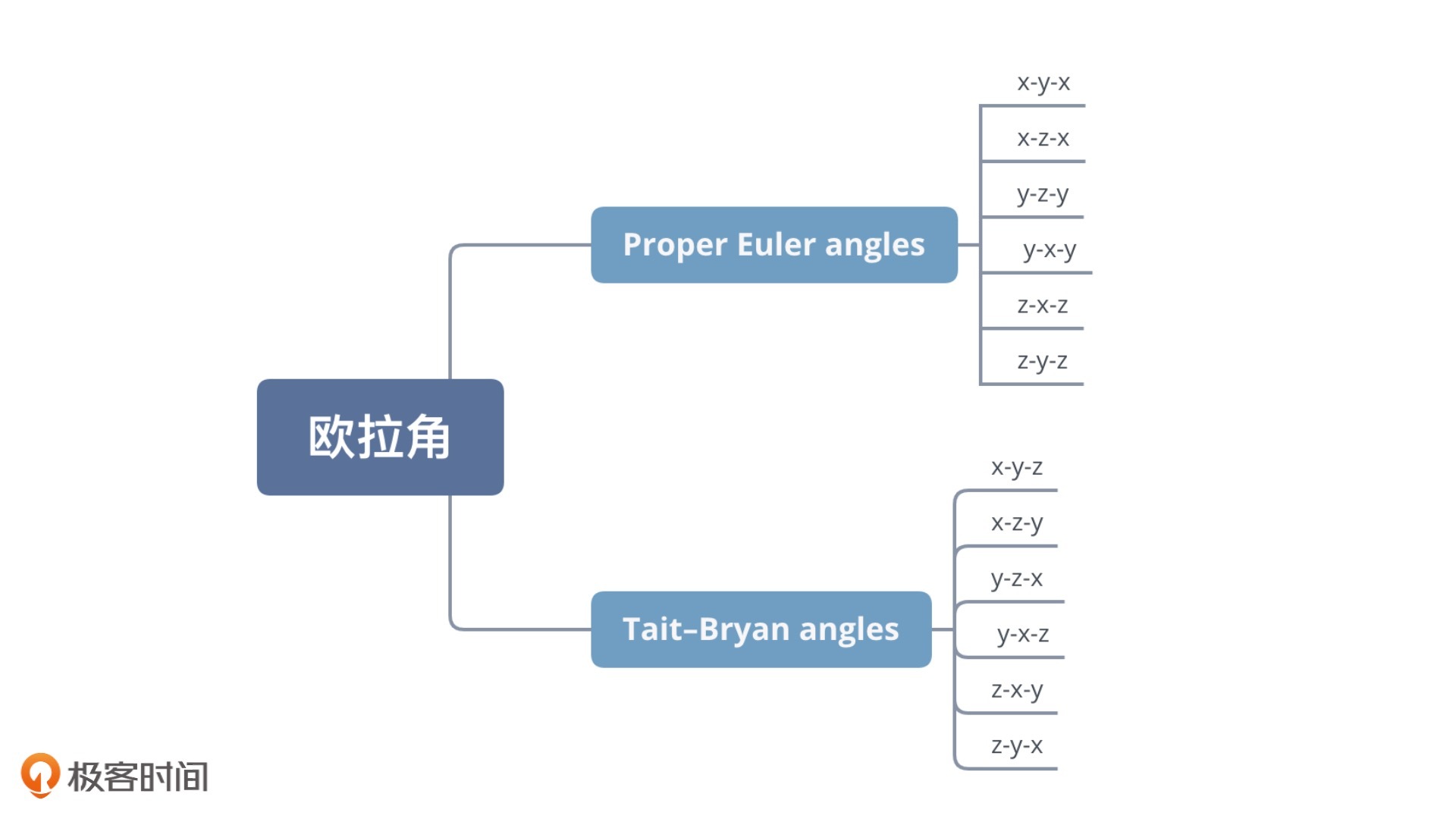
显然，我们采用的 $y-x-z$ 顺规，属于Tait–Bryan angles。

不同的欧拉角顺规虽然表示方法不同，但它们本质上还是欧拉角，都可以表示三维几何空间中的任意取向。所以，我们在绘制三维图形的时候，使用任何一种表示法都可以。今天，我就以$y-x-z$顺规为例来接着讲。

采用$y-x-z$顺规的欧拉角之后，我们能得到如下的旋转矩阵结果：

如何使用欧拉角来旋转几何体？

接下来，我们通过一个例子来实际体会，使用欧拉角旋转几何体的具体过程。

这里，我们还是用OGL框架。OGL的几何网格（Mesh）对象直接支持欧拉角，我们直接用对象的rotation属性就可以设置欧拉角，rotation属性是一个三维向量，它的$x、y、z$坐标就对应围绕$x、y、z$旋转的欧拉角。而且OGL框架默认的欧拉角顺规是$y-x-z$。

为了增加趣味性，我们不用立方体、圆柱体这些一般几何体，而是旋转一个飞机的几何模型。

在OGL中，我们可以加载JSON文件，来载入预先设计好的几何模型。

下面就是我先封装好的，一个加载几何模型的函数。这个函数会载入JSON文件的内容，然后根据其中的数据创建Geometry对象，并返回这个对象。

async function loadModel(src) {
  const data = await (await fetch(src)).json();

  const geometry = new Geometry(gl, {
    position: {size: 3, data: new Float32Array(data.position)},
    uv: {size: 2, data: new Float32Array(data.uv)},
    normal: {size: 3, data: new Float32Array(data.normal)},
  });

  return geometry;
}

这样，我们通过如下指令，就可以加载飞机几何体模型了。

const geometry = await loadModel('../assets/airplane.json');

这里的assets/airplane.json是一份几何模型文件，内容类似于下面这样：

{
  "position": [0.752, 1.061, 0.0, 0.767...],
  "normal": [0.975, 0.224, 0.0, 0.975...],
  "uv": [0.745, 0.782, 0.705, 0.769...]
}

其中position、normal、uv是顶点数据，我们比较熟悉，分别是顶点坐标、法向量和纹理坐标。这样的数据一般是由设计工具直接生成的，不需要我们来计算。

接下来，我们加载飞机的纹理图片，同样要先封装一个加载图片纹理的函数。在函数里，我们用img元素加载图片，然后将图片赋给对应的纹理对象。函数代码如下：

function loadTexture(src) {
  const texture = new Texture(gl);
  return new Promise((resolve) => {
    const img = new Image();
    img.onload = () => {
      texture.image = img;
      resolve(texture);
    };
    img.src = src;
  });
}

接着，我们就可以加载飞机的纹理图片了。具体操作如下：

const texture = await loadTexture('../assets/airplane.jpg');

然后，我们在片元着色器中，直接读取纹理图片中的颜色信息：

precision highp float;

uniform sampler2D tMap;
varying vec2 vUv;

void main() {
  gl_FragColor = texture2D(tMap, vUv);
}

最后，我们就能将元素渲染出来了。渲染指令如下：

const program = new Program(gl, {
  vertex,
  fragment,
  uniforms: {
    tMap: {value: texture},
  },
});
const mesh = new Mesh(gl, {geometry, program});
mesh.setParent(scene);
renderer.render({scene, camera});

最终，我们就能得到可以随意调整欧拉角的飞机模型了，效果如下图所示：

如何理解万向节锁？

使用欧拉角来操作几何体的方向，虽然很简单，但是有一个小缺陷，这个缺陷叫做万向节锁(Gimbal Lock)。那万向节锁是什么呢，我们通过上面的例子来解释。

你会发现，当我们分别改变飞机的alpha、beta、theta值时，飞机会做出对应的姿态调整，包括偏航（改变alpha）、翻滚（改变beta）和俯仰（改变theta）。

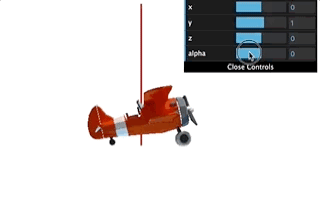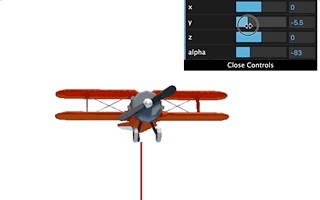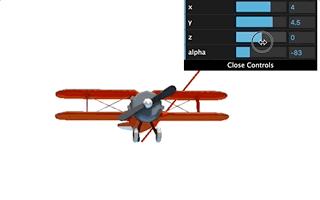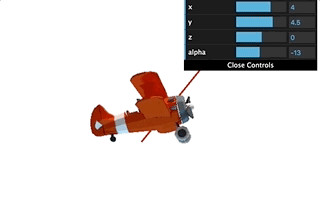
但是如果我们将beta固定在正负90度，改变alpha和beta，我们会发现一个奇特的现象：

如上图所示，我们将beta设为90度，不管改变alpha还是改变theta，飞机都绕着$y$轴旋转，始终处于一个平面上。也就是说，本来飞机姿态有$x、y、z$三个自由度，现在$y$轴被固定了，只剩下两个自由度了，这就是万向节锁。

万向节锁，并不是真的“锁”住。而是在特定的欧拉角情况下，姿态调整的自由度丢失了。而且，只要是欧拉角，不管我们使用哪一种顺规，万向节锁都会存在。这该怎么解决呢？

要避免万向节锁的产生，我们只能使用其他的数学模型，来代替欧拉角描述几何体的旋转。其中一个比较好的模型是四元数（Quaternion）。

使用四元数来旋转几何体

四元数是一种高阶复数，一个四元数可以表示为：$q = w + xi + yj + zk$。其中，$i、j、k$是三个虚数单位，$w$是标量，它们满足$i^{2} = j^{2} = k^{2} = ijk = -1$。如果我们把 $xi + yj + zk$ 看成是一个向量，那么四元数$q$又可以表示为 $q=(v, w)$，其中$v$是一个三维向量。

我们可以用单位四元数来描述3D旋转。所谓单位四元数，就是其中的参数满足 $x^{2} + y^{2} + z^{2} + w^{2}= 1$。单位四元数对应的旋转矩阵如下：

$$
R(q)=\left[\begin{array}{ccc}
1-2 y^{2}-2 z^{2} & 2 x y-2 z w & 2 x z+2 y w \\\
2 x y+2 z w & 1-2 x^{2}-2 z^{2} & 2 y z-2 x w \\\
2 x z-2 y w & 2 y z+2 x w & 1-2 x^{2}-2 y^{2}
\end{array}\right]
$$

这个旋转矩阵的数学推导过程比较复杂，我们只要记住这个公式就行了。

与欧拉角相比，四元数没有万向节死锁的问题。而且与旋转矩阵相比，四元数只需要四个分量就可以定义，模型上更加简洁。但是，四元数相对来说没有旋转矩阵和欧拉角那么直观。

四元数与轴角

四元数有一个常见的用途是用来处理轴角。所谓轴角，就是在三维空间中，给定一个由单位向量表示的轴，以及一个旋转角度$⍺$，以此来表示几何体绕该轴旋转$⍺$角。

绕单位向量$u$旋转$⍺$角，对应的四元数可以表示为：$q = (usin(⍺/2), cos(⍺/2))$。接着，我们来看一个四元数处理轴角的例子。

还是以前面飞机为例，不过，这次我们将欧拉角换成轴角，实现一个updateAxis和updateQuaternion函数，分别更新轴和四元数。

// 更新轴
function updateAxis() {
  const {x, y, z} = palette;
  const v = new Vec3(x, y, z).normalize().scale(10);
  points[1].copy(v);
  axis.updateGeometry();
  renderer.render({scene, camera});
}

// 更新四元数
function updateQuaternion(val) {
  const theta = 0.5 * val / 180 * Math.PI;
  const c = Math.cos(theta);
  const s = Math.sin(theta);
  const p = new Vec3().copy(points[1]).normalize();
  const q = new Quat(p.x * s, p.y * s, p.z * s, c);
  mesh.quaternion = q;
  renderer.render({scene, camera});
}

然后，我们定义轴，再把它显示出来。在OGL里面，我们可以通过Polyline对象来绘制轴。代码如下：

const points = [
  new Vec3(0, 0, 0),
  new Vec3(0, 10, 0),
];

const axis = new Polyline(gl, {
  points,
  uniforms: {
    uColor: {value: new Color('#f00')},
    uThickness: {value: 3},
  },
});
axis.mesh.setParent(scene);

那么，随着我们修改轴或者修改旋转角，物体就会绕着轴旋转。效果如下图所示：

这样，我们就实现了用四元数让飞机沿着某个轴旋转的效果了。这其中最重要的一步，是要你理解怎么根据旋转轴和轴角来计算对应的四元数，也就是updateQuaternion函数里面做的事情。然后我们将这个更新后的四元数赋给飞机的mesh对象，就可以更新飞机的位置，实现飞机绕轴的旋转。我只在课程中给出了关键部分的代码，你可以去GitHub仓库里找到对应例子的完整代码。

要点总结

今天，我们学习了使用三维仿射变换，来移动和旋转3D物体。三维仿射变换在平移和缩放变换上的绘制方法，与二维仿射变换类似，只不过增加了一个z维度。但是对于旋转变换，三维放射变换就要复杂一些了，因为3D物体可以绕$x、y、z$轴中任意一个方向旋转。

那想要旋转三维几何体，我们可以使用欧拉角。欧拉角实际上就等于，绕$x、y、z$三个轴方向的旋转矩阵相乘，相乘的顺序就是欧拉角的顺规。

虽然顺规有很多种，但是选择不同的顺规，只是表达方式不一样，最终结果是等价的，都是欧拉角。那在这节课中，我们采用$y-x-z$顺规，它也是OGL库默认采用的。

但是欧拉角有一个万向节锁的问题，就是当$β$角旋转到正负90度的时候，我们无论怎么改变$α、γ$角，都只能让物体在一个水平面上运动。而且，只要我们使用欧拉角，就无法避免万向节锁的出现。

为了避免万向节锁，我们可以用四元数来旋转几何体。除此之外，四元数还有一个作用是可以用来构造轴角，让物体沿着某个具体的轴旋转。你可以回想一下我们刚刚实现的绕轴飞行的飞机。

小试牛刀

你可以试着利用放射变换，来实现一个旋转的3D陀螺效果。陀螺的形状可以用一个简单的圆锥体来表示。旋转的过程中，你可以让陀螺绕自身的中间轴旋转，也可以让它绕着三维空间某个固定的轴旋转。快来动手试一试吧。效果如下：

除了旋转的飞机和旋转的陀螺，你还能实现哪些旋转的物体呢？不如也把这篇文章分享给你的朋友们，一起来实现一下吧！

源码

课程中详细示例代码GitHub仓库