
你好,我是月影。
在我们生活的真实物理世界中,充满了各种类型的光。在这些光的照射下,我们看到的每个物体都会呈现不同的色彩。所以,要想让我们渲染出的3D物体看起来更自然、逼真,很重要的一点就是模拟各种光照的效果。那今天,我们就一起来学习一下,怎么模拟光照效果。
物体的光照效果是由光源、介质(物体的材质)和反射类型决定的,而反射类型又由物体的材质特点决定。在3D光照模型中,根据不同的光源特点,我们可以将光源分为4种不同的类型,分别是环境光(Ambient Light)、平行光(Directional Light)、点光源(Positional Light)和聚光灯(Spot Light)。而物体的反射类型,则分为漫反射和镜面反射两种。
当然了,实际自然界中的光照效果,肯定比我说的要复杂得多。但现阶段,我们弄明白这三个决定因素,就能模拟出非常真实的光照效果了。
我们先来说说怎么给物体增加环境光效果。
那什么是环境光呢?环境光就是指物体所在的三维空间中天然的光,它充满整个空间,在每一处的光照强度都一样。环境光没有方向,所以,物体表面反射环境光的效果,只和环境光本身以及材质的反射率有关。
物体在环境光中呈现的颜色,我们可以利用下面的公式来求。其中,环境光的颜色为$L$,材质对光的反射率为$R$。
$$
C=L R=\left[\begin{array}{c}
L_{r} \times R_{r} \\\
L_{g} \times R_{g} \\\
L_{b} \times R_{b}
\end{array}\right]
$$
接着,我们创建一个片元着色器,代码如下:
precision highp float;
uniform vec3 ambientLight;
uniform vec3 materialReflection;
void main() {
gl_FragColor.rgb = ambientLight * materialReflection;
gl_FragColor.a = 1.0;
}
我们用这个着色器创建WebGL着色器程序,传入环境光ambientLight和材质反射率materialReflection,就可以渲染出各种颜色的几何体了。

那你可能有疑问了,通过这样渲染出来的几何体颜色,与我们之前通过设置颜色属性得到的颜色有什么区别呢?
在前面的课程里,我们绘制的几何体只有颜色属性,但是在光照模型里,我们把颜色变为了环境光和反射率两个属性。这样的模型更加接近于真实世界,也让物体的颜色有了更灵活的控制手段。比如,我们修改环境光,就可以改变整个画布上所有受光照模型影响的几何体的颜色,而如果只是像之前那样给物体分别设置颜色,我们就只能一一修改这些物体各自的颜色了。
最后,我希望你能记住环境光的两个特点。
首先,因为它在空间中均匀分布,所以在任何位置上环境光的颜色都相同。其次,它与物体的材质有关。如果物体的RGB通道反射率不同的话,那么它在相同的环境光下就会呈现出不同的颜色。因此,如果环境光是白光(#FFF),那么物体呈现的颜色就是材质反射率表现出的颜色,也就是物体的固有颜色。
除了环境光以外,平行光也很常见。与环境光不同,平行光是朝着某个方向照射的光,它能够照亮几何体的一部分表面。
而且,平行光除了颜色这个属性之外,还有方向,它属于有向光。有向光在与物体发生作用的时候,根据物体的材质特性,会产生两种反射,一种叫做漫反射(Diffuse reflection),另一种叫做镜面反射(Specular reflection),而一个物体最终的光照效果,是漫反射、镜面反射以及我们前面说的环境光叠加在一起的效果。因为内容比较多,所以这节课,我们先来讨论光源的漫反射效果。下节课,我们再继续讨论光源的镜面反射,以及多个光源混合的反射效果。如下图所示:
有向光的漫反射在各个方向上的反射光均匀分布,反射强度与光的射入方向与法线的夹角的余弦成正比。
那我们该如何让3D物体呈现出,平行光照射下的颜色效果呢?下面,我就以添加一道白色的平行光为例,来具体说说操作过程。
首先,我们在顶点着色器中添加一道平行光。具体来说就是传入一个directionalLight向量。为什么是顶点着色器呢?因为,我们在顶点着色器中计算光线的方向,需要运算的次数少,会比在片元着色器中计算的性能要好很多。
precision highp float;
attribute vec3 position;
attribute vec3 normal;
uniform mat4 modelViewMatrix;
uniform mat4 projectionMatrix;
uniform mat4 viewMatrix;
uniform mat3 normalMatrix;
uniform vec3 directionalLight;
varying vec3 vNormal;
varying vec3 vDir;
void main() {
// 计算光线方向
vec4 invDirectional = viewMatrix * vec4(directionalLight, 0.0);
vDir = -invDirectional.xyz;
// 计算法向量
vNormal = normalize(normalMatrix * normal);
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
}
然后,在片元着色器里,我们计算光线方向与法向量夹角的余弦,计算出漫反射光。在平行光下,物体最终呈现的颜色是环境光加上漫反射光与材质反射率的乘积。
precision highp float;
uniform vec3 ambientLight;
uniform vec3 materialReflection;
uniform vec3 directionalLightColor;
varying vec3 vNormal;
varying vec3 vDir;
void main() {
// 求光线与法线夹角的余弦
float cos = max(dot(normalize(vDir), vNormal), 0.0);
// 计算漫反射
vec3 diffuse = cos * directionalLightColor;
// 合成颜色
gl_FragColor.rgb = (ambientLight + diffuse) * materialReflection;
gl_FragColor.a = 1.0;
}
接着,我们在JavaScript代码里,给WebGL程序添加一个水平向右的白色平行光,代码如下:
const ambientLight = {value: [0.5, 0.5, 0.5]};
const directional = {
directionalLight: {value: [1, 0, 0]},
directionalLightColor: {value: [1, 1, 1]},
};
const program1 = new Program(gl, {
vertex,
fragment,
uniforms: {
ambientLight,
materialReflection: {value: [0, 0, 1]},
...directional,
},
});
...
最终显示的效果如下图所示,当旋转相机位置的时候,我们看到物体因为光照,不同方向表面的明暗度不一样。
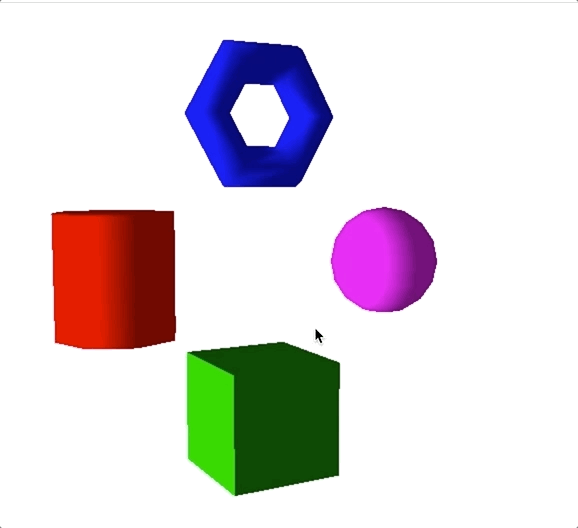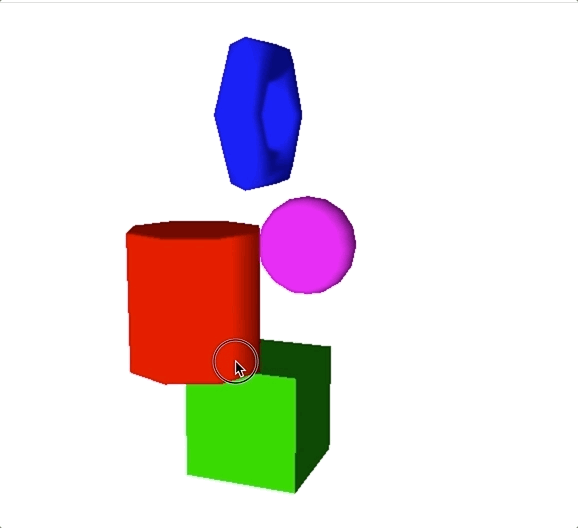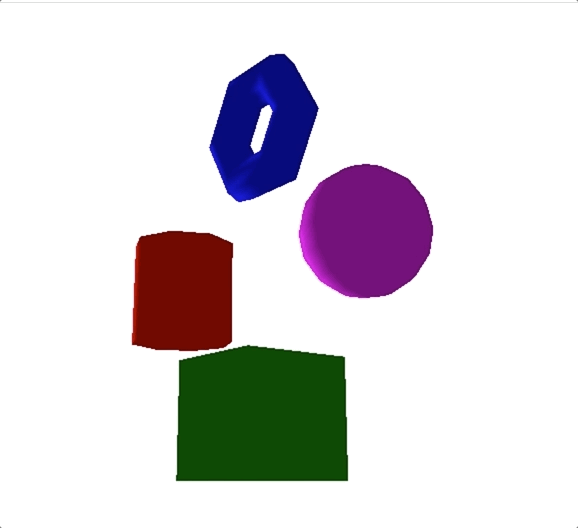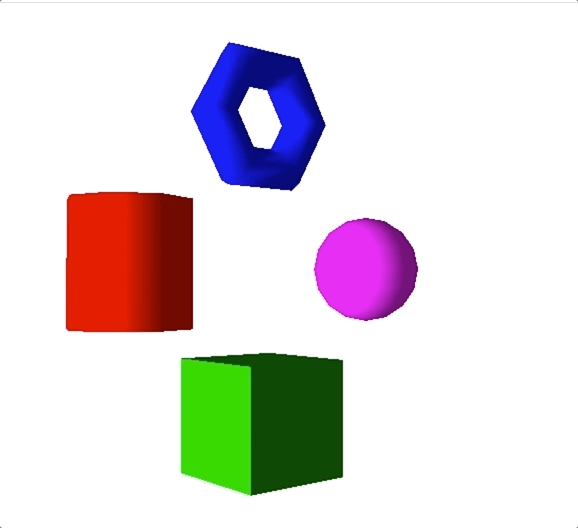
除了平行光之外,点光源和聚光灯也都是有向光。
点光源顾名思义,就是指空间中某一点发出的光,与方向光不同的是,点光源不仅有方向属性,还有位置属性。因此计算点光源的光照,我们要先根据光源位置和物体表面相对位置来确定方向,然后再和平行光一样,计算光的方向和物体表面法向的夹角。计算过程要比平行光稍微复杂一些。
对于平行光来说,只要法向量相同,方向就相同,所以我们可以直接在顶点着色器中计算方向。但点光源因为其方向与物体表面的相对位置有关,所以我们不能在顶点着色器中计算,需要在片元着色器中计算。
因此,计算点光源光照效果的第一步,就是要在顶点着色器中,将物体变换后的坐标传给片元着色器,代码如下:
precision highp float;
attribute vec3 position;
attribute vec3 normal;
uniform mat4 modelViewMatrix;
uniform mat4 projectionMatrix;
uniform mat3 normalMatrix;
varying vec3 vNormal;
varying vec3 vPos;
void main() {
vPos = modelViewMatrix * vec4(position, 1.0);;
vNormal = normalize(normalMatrix * normal);
gl_Position = projectionMatrix * vPos;
}
那接下来,片元着色器中的计算过程就和平行光类似了。 我们要计算光线方向与法向量夹角的余弦,我们用 (viewMatrix * vec4(pointLightPosition, 1.0)).xyz - vPos 得出点光源与当前位置的向量,然后用这个向量和法向量计算余弦值,这样就得到了我们需要的漫反射余弦值。对应的片元着色器如下:
precision highp float;
uniform vec3 ambientLight;
uniform vec3 materialReflection;
uniform vec3 pointLightColor;
uniform vec3 pointLightPosition;
uniform mat4 viewMatrix;
varying vec3 vNormal;
varying vec3 vPos;
void main() {
// 光线到点坐标的方向
vec3 dir = (viewMatrix * vec4(pointLightPosition, 1.0)).xyz - vPos;
// 与法线夹角余弦
float cos = max(dot(normalize(dir), vNormal), 0.0);
// 计算漫反射
vec3 diffuse = cos * pointLightColor;
// 合成颜色
gl_FragColor.rgb = (ambientLight + diffuse) * materialReflection;
gl_FragColor.a = 1.0;
}
假设我们将点光源设置在(3,3,0)位置,颜色为白光,得到的效果如下图所示。
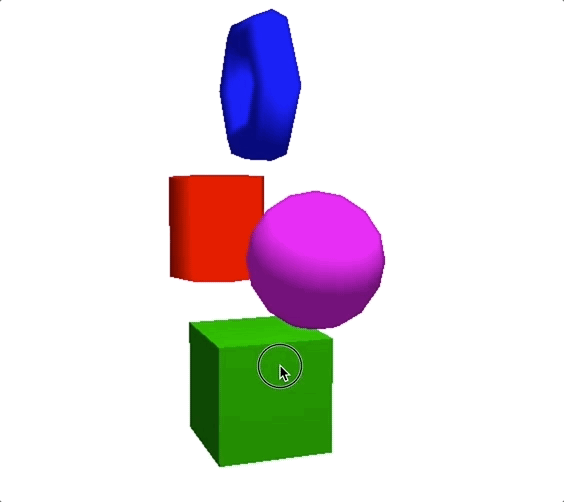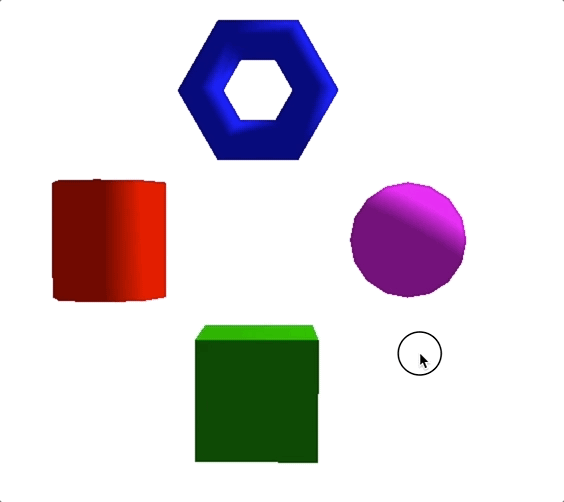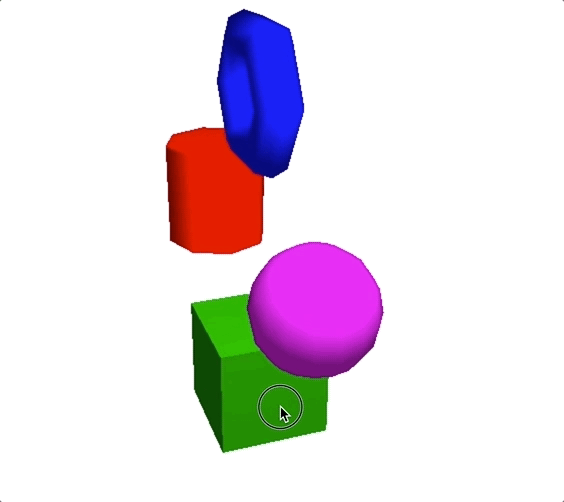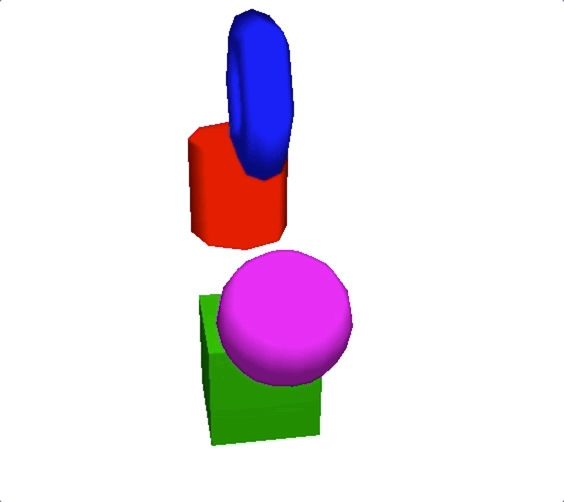
但是,前面的计算过程都是理想状态下的。而真实世界中,点光源的光照强度会随着空间的距离增加而衰减。所以,为了实现更逼真的效果,我们必须要把光线衰减程度也考虑进去。光线的衰减程度,我们一般用衰减系数表示。衰减系数等于一个常量$d_{0}$(通常为1),除以衰减函数$p$。
一般来说,衰减函数可以用一个二次多项式$P$来描述,它的计算公式为:
$$
\left\{\begin{array}{l}
P=A z^{2}+B z+C \\\
d=\frac{d_{0}}{P}
\end{array}\right.
$$
其中$A、B、C$为常量,它们的取值会根据实际的需要随时变化,$z$是当前位置到点光源的距离。
接下来,我们需要在片元着色器中增加衰减系数。在计算的时候,我们必须要提供光线到点坐标的距离。具体的操作代码如下:
precision highp float;
uniform vec3 ambientLight;
uniform vec3 materialReflection;
uniform vec3 pointLightColor;
uniform vec3 pointLightPosition;
uniform mat4 viewMatrix;
uniform vec3 pointLightDecayFactor;
varying vec3 vNormal;
varying vec3 vPos;
void main() {
// 光线到点坐标的方向
vec3 dir = (viewMatrix * vec4(pointLightPosition, 1.0)).xyz - vPos;
// 光线到点坐标的距离,用来计算衰减
float dis = length(dir);
// 与法线夹角余弦
float cos = max(dot(normalize(dir), vNormal), 0.0);
// 计算衰减
float decay = min(1.0, 1.0 /
(pointLightDecayFactor.x * pow(dis, 2.0) + pointLightDecayFactor.y * dis + pointLightDecayFactor.z));
// 计算漫反射
vec3 diffuse = decay * cos * pointLightColor;
// 合成颜色
gl_FragColor.rgb = (ambientLight + diffuse) * materialReflection;
gl_FragColor.a = 1.0;
}
假设,我们将衰减系数设置为(0.05, 0, 1),就能得到如下效果。把它和前一张图对比,你会发现,我们看到较远的几何体几乎没有光照了。这就是因为光线强度随着距离衰减了,也就更接近真实世界的效果。
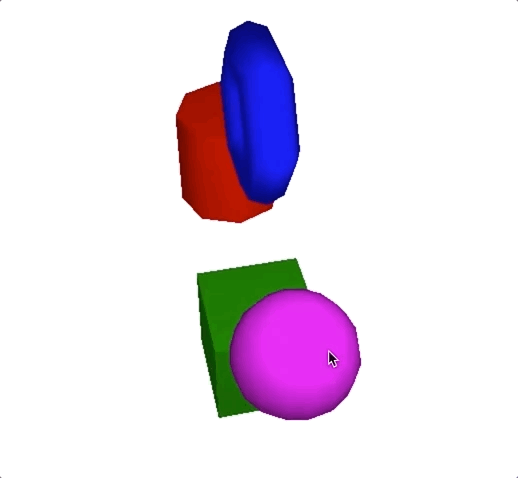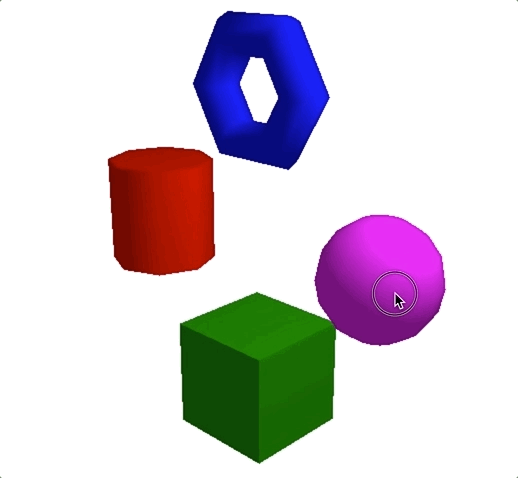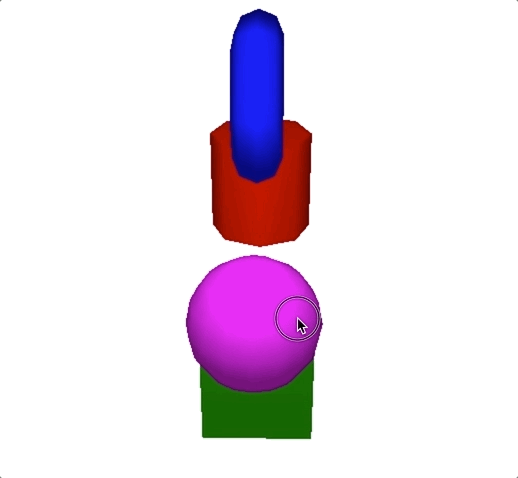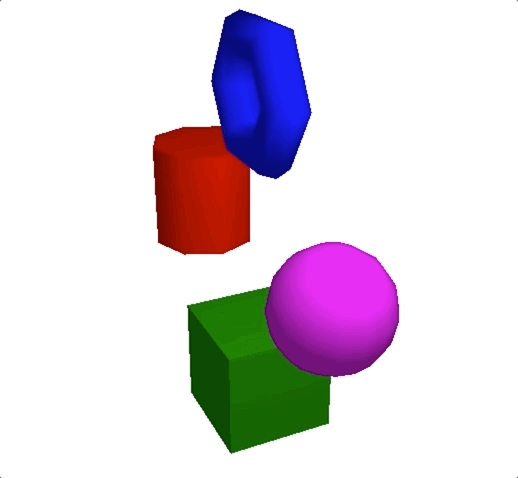
最后,我们再来说说,怎么给物体添加聚光灯效果。
与点光源相比,聚光灯增加了方向以及角度范围,只有在这个范围内,光线才能照到。那该如何判断坐标是否在角度范围内呢?我们可以根据法向量与光线方向夹角的余弦值来判断坐标是否在夹角内,还记得我们在第6节课一开始就讨论的那道题目吗,这里就是具体应用。
所以,最终片元着色器中的代码如下:
precision highp float;
uniform mat4 viewMatrix;
uniform vec3 ambientLight;
uniform vec3 materialReflection;
uniform vec3 spotLightColor;
uniform vec3 spotLightPosition;
uniform vec3 spotLightDecayFactor;
uniform vec3 spotLightDirection;
uniform float spotLightAngle;
varying vec3 vNormal;
varying vec3 vPos;
void main() {
// 光线到点坐标的方向
vec3 invLight = (viewMatrix * vec4(spotLightPosition, 1.0)).xyz - vPos;
vec3 invNormal = normalize(invLight);
// 光线到点坐标的距离,用来计算衰减
float dis = length(invLight);
// 聚光灯的朝向
vec3 dir = (viewMatrix * vec4(spotLightDirection, 0.0)).xyz;
// 通过余弦值判断夹角范围
float ang = cos(spotLightAngle);
float r = step(ang, dot(invNormal, normalize(-dir)));
// 与法线夹角余弦
float cos = max(dot(invNormal, vNormal), 0.0);
// 计算衰减
float decay = min(1.0, 1.0 /
(spotLightDecayFactor.x * pow(dis, 2.0) + spotLightDecayFactor.y * dis + spotLightDecayFactor.z));
// 计算漫反射
vec3 diffuse = r * decay * cos * spotLightColor;
// 合成颜色
gl_FragColor.rgb = (ambientLight + diffuse) * materialReflection;
gl_FragColor.a = 1.0;
}
如上面代码所示,聚光灯相对来说比较复杂,我们要用整整5个参数来描述,它们分别是:
在计算光线和法线夹角的余弦值时,我们是用与点光源一样的方式。此外,我们还增加了一个步骤,就是以聚光灯方向和角度,计算点坐标是否在光照角度内。如果在,那么r的值是1,否则r的值是0。
假设我们是这样设置的,那么最终的光照效果就只会出现在光照的角度内。
const directional = {
spotLightPosition: {value: [3, 3, 0]},
spotLightColor: {value: [1, 1, 1]},
spotLightDecayFactor: {value: [0.05, 0, 1]},
spotLightDirection: {value: [-1, -1, 0]},
spotLightAngle: {value: Math.PI / 12},
};
我们最终渲染出来的结果如下图:
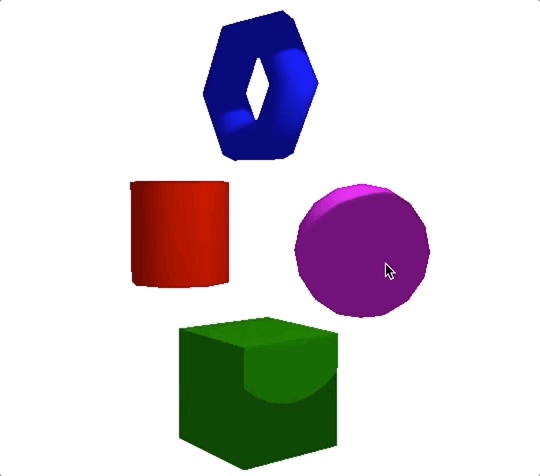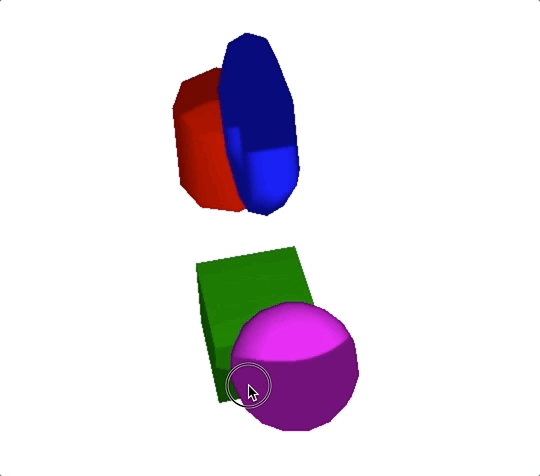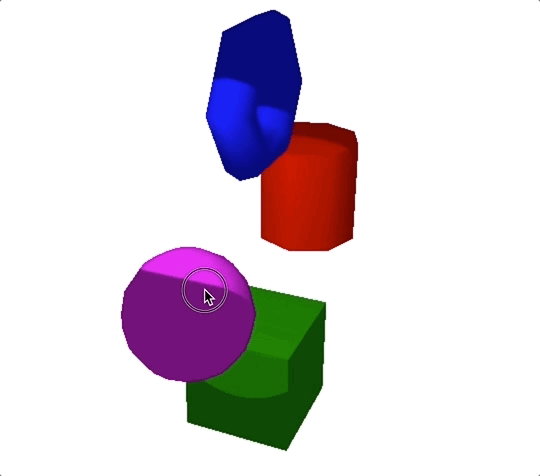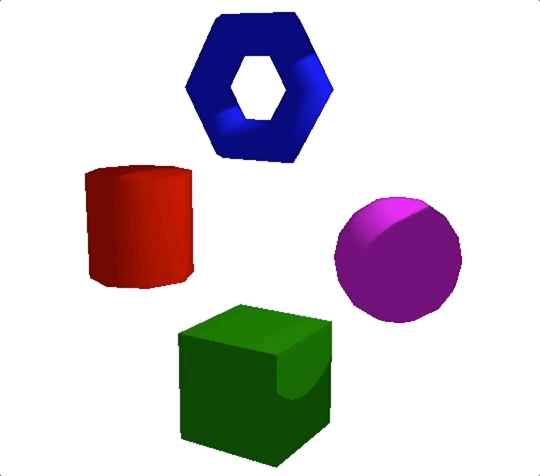
在这一节课,我们主要讲了模拟真实世界中4种不同光源的方法,这四种不同光源分别是环境光、平行光、点光源和聚光灯。
其中,环境光比较简单,它充满整个环境空间,在空间每一处的强度都相同。环境光作用于物体材质,根据材质对光的反射率,让材质呈现出不同的颜色。
另外三种光是有向光,它们作用于物体表面的效果,除了与物体材质的反射率有关,还和表面的朝向有关,所以我们需要计算光线方向和表面法向量的余弦值,用它来计算反射强度。
这三种光当中,平行光只有方向和颜色两个参数,点光源有位置、颜色和衰减系数三个参数,而聚光灯更加复杂,有位置、方向、角度范围、颜色和衰减系数五个参数。我们在着色器中根据这些参数进行计算,最终就能得到物体被光照后的漫反射结果。
你会发现,这节课,我举的都是单一光源的例子,也就是空间中除了环境光以外,只有一个光源。但在真实的世界里,空间中肯定不止一种光源。你能试着修改例子中的代码,添加多个光源,让它们共同作用于物体吗?会实现什么样的效果呢?
欢迎在留言区分享你的答案和思考,也希望你能把这节课的内容转发出去,我们下节课再见!
本课中完整的示例代码见 GitHub仓库
评论