你好,我是月影。
刚刚学完了可视化的数学篇,今天咱们放松一下,以我的个人经历来聊一聊,数学对我们程序员的重要性。
作为奇舞团团长和从事前端15年以上的“老人”,我为团队面试过许多同学,也和许多同学聊过前端或者程序员的职业发展方向。一般来说,我面试的时候会要求面试者有一定的数学基础,在聊关于职业发展的话题时,我也会强调数学对于程序员成长的重要性。甚至,在可视化这门课里面,我也认为学习可视化的第一步是学好图形学相关的数学知识。
不过,行业里也有些不同的声音,有些人觉得除了部分特殊的领域,大部分普通的编程领域不太需要数学知识。比如说,在我们平时的Web开发项目中,不论是前端还是后端,似乎更多地是和产品与业务逻辑打交道,比较少或几乎没有用到数学知识。甚至有些人认为,程序员根本用不着学好数学,特别是在前端这样偏UI层的领域,数学更是没有用武之地。
当然,以上这些认为数学不重要的想法,我都可以理解,曾经我自己也没有意识到数学和编程有什么必然的联系。而且,我当年在学校学习的时候,数学也学得很马虎,基础也不是那么好。不过后来,我个人的一段经历,让我很早就意识到数学对编程的重要性,而这个认知,对我后来的职业发展有着非常重要的影响。所以,我想在这里和你分享一些我个人成长中的经历和收获,希望能对你有些帮助。
2003年,因为朋友的推荐,我获得了微软亚洲研究院(MSRA)访问学生的面试机会,当时的面试官是浙江大学的刘利刚博士,他也是我后来的实习导师。那时,他正在MSRA做访问学者。
在这之前,我没有任何面试经验,在学校里面,我的学习成绩也一般,只是对编程比较感兴趣,自己做过一些小项目。我不知道会被面试什么问题,所以也没特意准备。见到了利刚博士之后,他并没有问我任何有关编程的问题,而是问了我两个数学问题,这两个问题让我至今仍记忆犹新。
第一个问题是这样的:
已知ABC是三个不同的数字,且能使以下等式成立,求A、B、C分别是多少。

求这道题的答案并不是很难,但是花多久的时间能得出答案却是一个问题。我当时回答出这个问题,大概只用了不到10秒钟。你可以先试着解一下,看看你能在10秒内给出这个问题的答案吗?
其实,利刚博士出这道题,主要在考察我的数感。啥是数感呢?这不是指一个人具备了多么高深的数学知识,而是指他对数字的一种直觉以及洞察力。
我在解决这个问题的时候,完全是脱口而出答案,我甚至都没有意识到自己是怎么得出来的。但是,当我一下说出答案之后,再回想为什么才反应过来,这道题其实是有规律的。
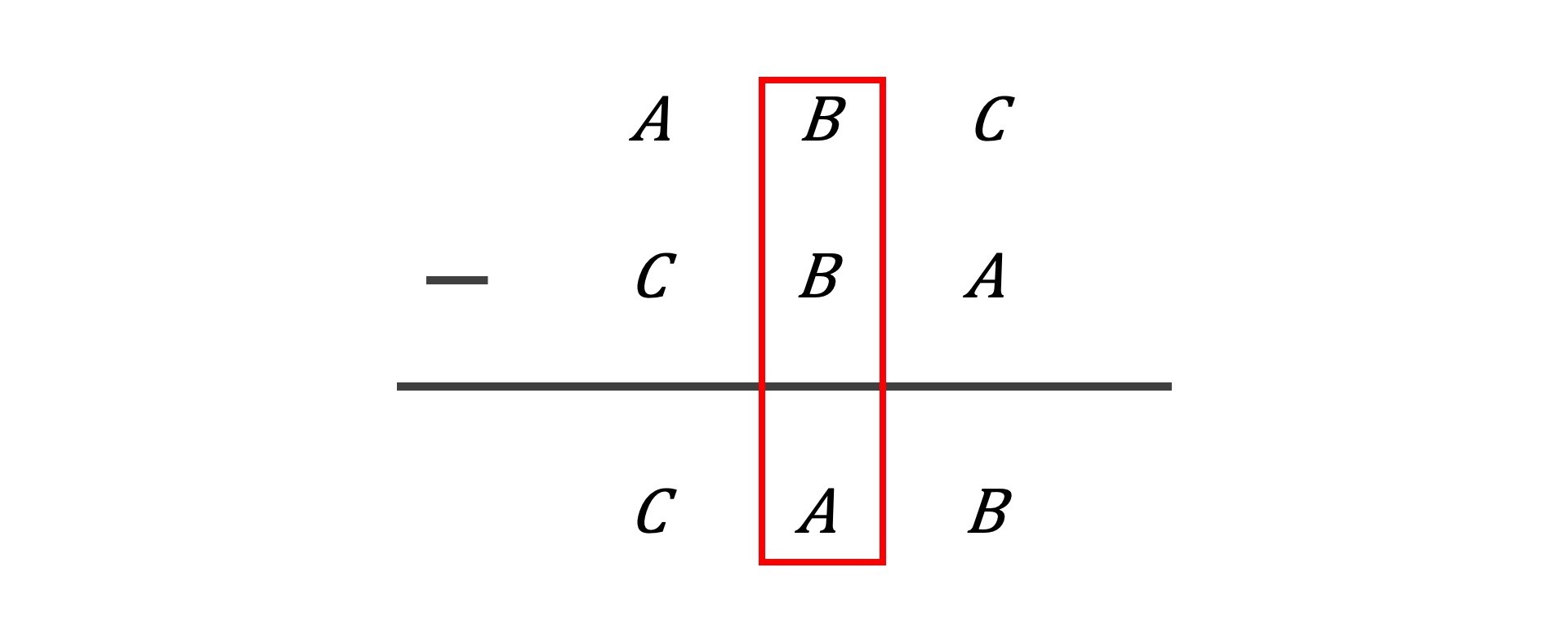
你仔细看中间这一列,应该能一下子得出A的值是9。然后再看第一列,就能得到C的值是4,最后B的值自然就是5了。所以答案就是A = 9、B = 5、C = 4。
那面试为啥要考察数感呢?利刚博士是这么给我解释的:数感好表示学习和理解能力强,因为访问学生要做的工作内容就是图形学的基础研究,一些知识肯定是要现学的,这需要有比较强的学习能力和理解力,所以作为数学基础的数感就很重要了。正是通过这个问题,我认识到了数感的重要性。
好了,接下来我们接着来看第二个问题。
给你一个天平和一个物体,让你设计一些砝码,无论这个物体的重量是在1~100克之间的任何一个整数克数,都能用这些砝码称量出来,并且砝码的数量要尽可能少,你最少需要几个砝码呢?
乍一看,这个问题似乎与计算机和编程完全不沾边,但实际上这个问题涉及基础的数的进制原理。为什么说这个天平称重涉及数的进制原理呢?
因为我们知道,天平一般来说标准的用法是左边托盘放物体,右边托盘放砝码。那如果我们要称重的物体在1~100克之间,还要设计尽可能少的砝码,最优解肯定是称某个克数的砝码组合是唯一的,这样最省砝码。
怎么理解呢?我举个例子。
假如说,现在我们有3个砝码,分别为A砝码1克、B砝码2克、C砝码也是2克,显然这3个砝码可以称1~5克的物体。如果物体是1克的话,那么用A砝码就行;如果物体是2克的话,有两种方法,用B砝码,或者用C砝码;如果物体是3克的话,也有两种方法,用A+B或A+C砝码;如果物体是4克的话,用B+C砝码,如果物体是5克的话,用A+B+C砝码。
但是我们看到,在物体是2克和3克的时候,分别有两种砝码组合对应的称量方法。如果我们把一种砝码组合作为一种编码,再把一种物体克数作为一个状态的话,那么重复的编码就只表示同一种状态,这就属于浪费。显然更好的解决办法,是用最少的编码组合表示尽可能多的状态。甚至我们应该做到一种编码唯一对应一种状态,这样才是最优的。
所以呢,我们应该把C砝码改为4克,这样一来,3个砝码就可以称出1~7克的物体,而且没有任何两种编码表示同一种状态,这就是最优的。我把具体的称量方法总结出一张表,列在了下面。
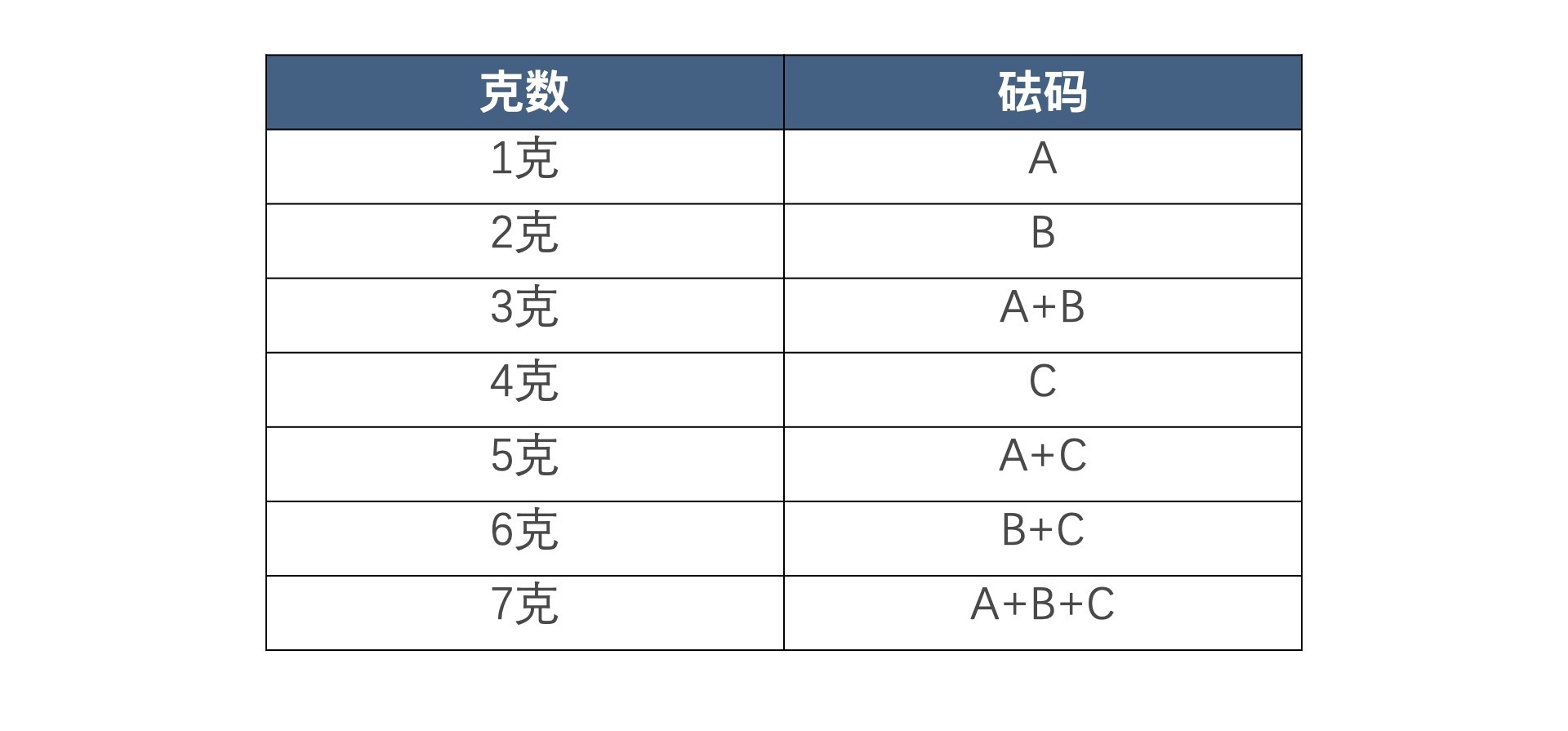
看到这里,聪明的同学应该已经知道这一题的答案了。实际上,我们将砝码被使用记为1,将砝码不被使用记为0,那这个问题就等价于:用多少位二进制数可以表示不大于100的正整数?因此,答案自然是7位,也就是说砝码需要7个,重量分别是1克、2克、4克、8克、16克、32克和64克。
所以你看,这个问题表面上是天平问题,实际上牵扯到数的进制表示,或者说是编码,这显然是一个计算机问题。这其实也是利刚博士问我这个问题的真正目的,它同时考查了我关于数学模型的抽象能力,以及对计算机基础知识的理解程度。
顺便再说一下,这个问题如果允许将砝码放在天平左侧托盘中,那么有一个技巧可以让用到的砝码数量更少,你能想到该怎么做吗?如果你想到了,可以在留言里分享你的答案。
回答出这两个问题之后,我通过了面试,来到微软亚洲研究院实习。我的课题是图形学基础研究,恰好是和三角剖分有关,具体来说是简单多边形的相容三角剖分。
什么是简单多边形的相容三角剖分呢?简单来说,就是将两个简单多边形剖分成同样数量的三角形,同时还需要保证每个三角形的顶点能够一一对应。所谓一一对应,就是给两个多边形的顶点进行编号之后,它们中每一对三角形顶点的编号都相同。
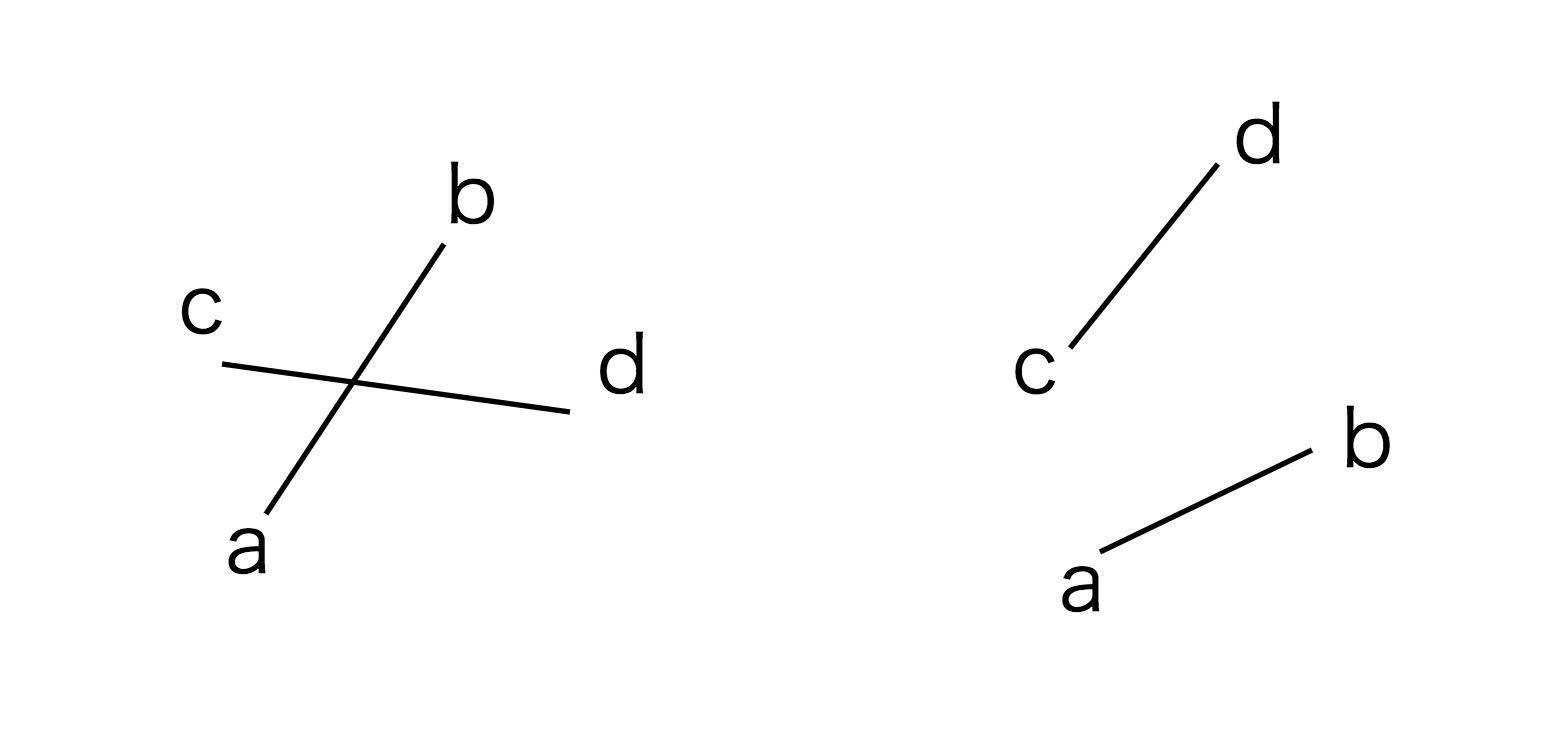
如果两个简单多边形的边数相同,在不允许添加内部点的情况下,并不总能构成相容三角剖分。比如下图中的两个六边形,左边三条虚线构成三角形,而右边的三条虚线却相交于一个点,所以对这两个图形来说,如果我们不添加内部点,就不存在相容三角剖分了。
如果我们允许在图形内部添加点进行三角剖分,就可以得到相容三角剖分了,剖分后的效果如下图:
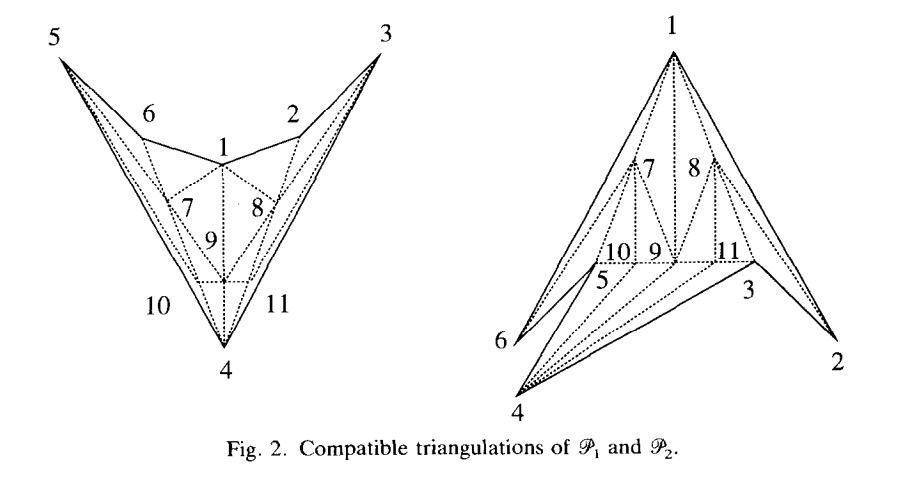
而我当时的工作主要是研究如何对多边形进行快速相容三角剖分。之所以研究相容三角剖分,是因为通过相容三角剖分可以生成拓扑结构相同的三角网格,而拓扑结构相同的三角网格是实现物体变形特效的基础。比如说,我们可以用相容三角剖分实现人物的“变脸”特效等等。
大体上,我的研究就是围绕相容三角剖分涉及的算法,因为它们都比较复杂,这里我就不多说了。接下来,我主要介绍一下我的工作中遇到的问题。因为涉及图形学的基础内容,自然会有一些基础的图形学计算,比如计算点到直线和线段的距离,计算边的切线和法线,判断线段的关系,绘制圆锥曲线等等。
在我刚开始实习的时候,第一个任务就是要计算点到直线和线段的距离。
不过,一开始我在求点到直线的距离的时候,是先写出直线的两点式代数方程,然后求点与直线的垂线方程,接着将两个方程联立求交点,最后再求出点与交点的距离。
这么做当然是可以求出结果来的,但是计算过程可以说是相当繁琐了,而且它还有缺陷。缺陷究竟是什么呢?我们知道,用直线方程求垂线的时候,要用到点斜式,但是点斜式的斜率,在直线垂直于X轴时,会有斜率计算出来是无穷大的问题。这种特殊情况还需要特殊处理,就更增加了我计算的复杂度。
所以,当时我花了一天时间才把“求点到直线和线段距离的问题”用代数方程解决。但是,第二天给利刚博士交差的时候,就被他批评了一顿,他问我为什么要用代数方程去做这个问题,如果用向量来做,根本就是分分钟的事儿。
如果你认真学了数学篇的课程,应该也已经知道,用向量解决这个问题的确非常简单。因为向量叉积的几何意义就是平行四边形的面积,在用向量叉积除以底边就是高,也就是点到向量所在直线的距离了。而我当时并没有想起可以用向量来解决这类问题,所以才走了弯路。
经过这次教训,我深刻意识到选择正确数学工具,能够把看似非常复杂的问题转化为简简单单问题,从而顺利解决。这也是为什么数学对于程序员来说非常重要。这个教训也是我在MSRA实习中最重要的收获。
大约4个多月后,我就结束了MSRA的实习,回到了学校。毕业后,我去了一家深圳的软件公司,真正地成为了一名程序员。后来更是在机缘巧合下接触到了前端,也一直成长到今天。
在成长的过程中,我始终牢记:用数学思想和意识去解决工作中的问题。你别说,还真被我遇到了两个事儿。接下来,我就和你说说我印象最深刻的这两个案例。
第一个案例是我在08年到百度时遇到的。当时,某个产品中有一个绘制椭圆的需求,负责开发的工程师是使用椭圆的代数方程来计算的。因为代数方程涉及开平方的问题,所以开发人员还要根据象限来判断正负号,这会非常麻烦。
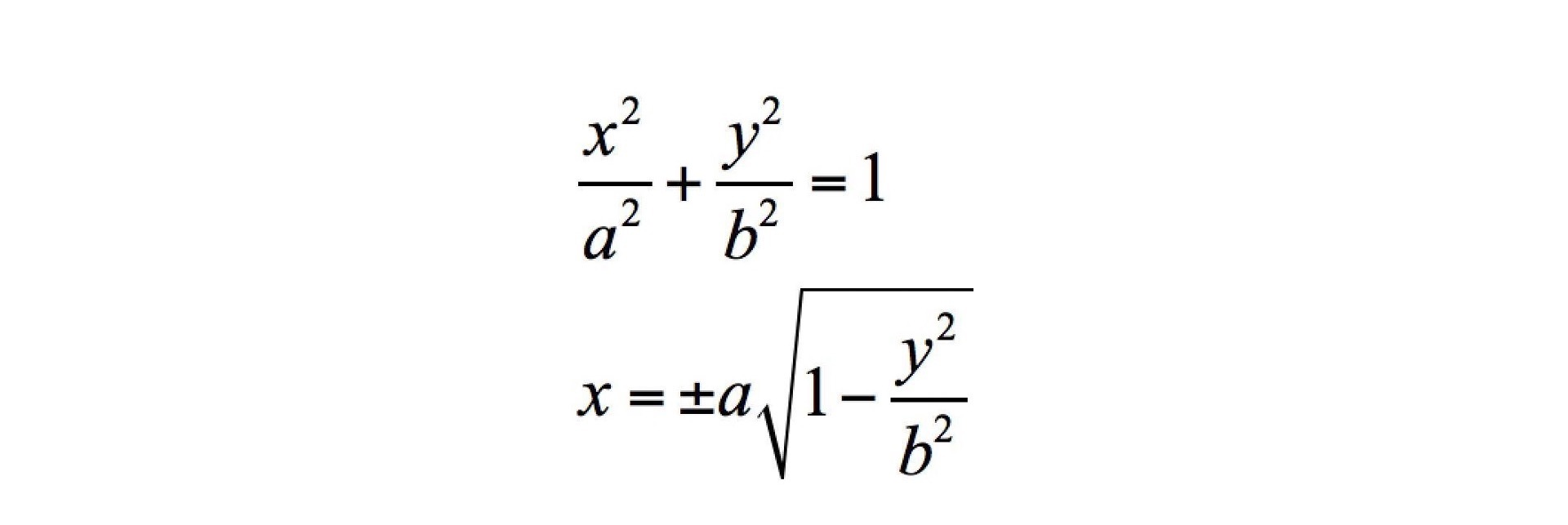
现在你学习了数学篇的课程,应该知道用椭圆的参数方程来解决,根本不会涉及开根号和象限判断问题,操作起来也会简单很多。
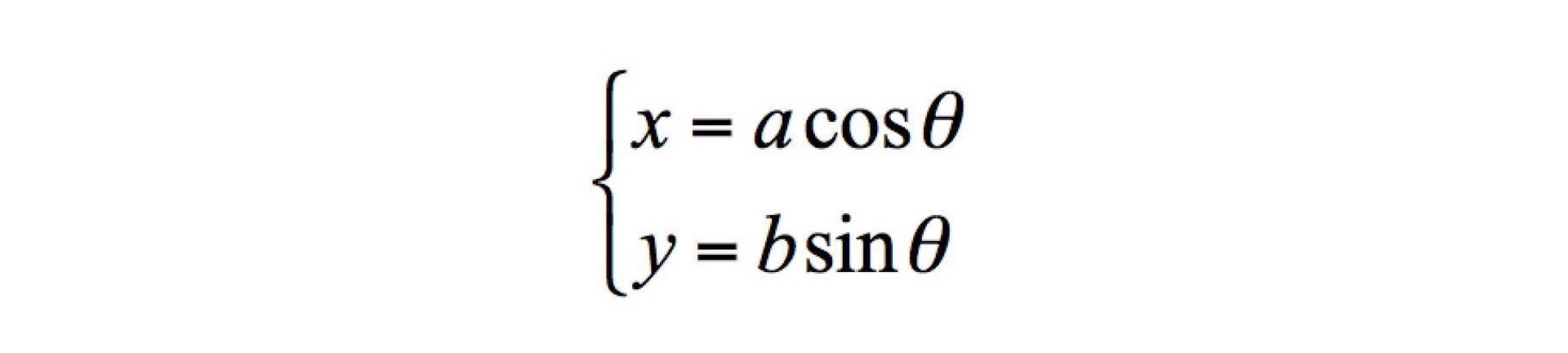
另一个案例,是我在360搜索的一个运营活动中遇到的。当时需要我们实现一个Canvas2D的图片特效,效果如下:

具体要求是在一张静态图片上,选择若干个运动区域,比如示意图中的猫的耳朵、眼睛、鼻子区域,然后对区域做这样逆时针旋转的运动,最终将它变为动图。
这其实是一个Canvas2d的特效。最初的时候,我们的工程师是使用代数方法来解决的,具体的方法如下:
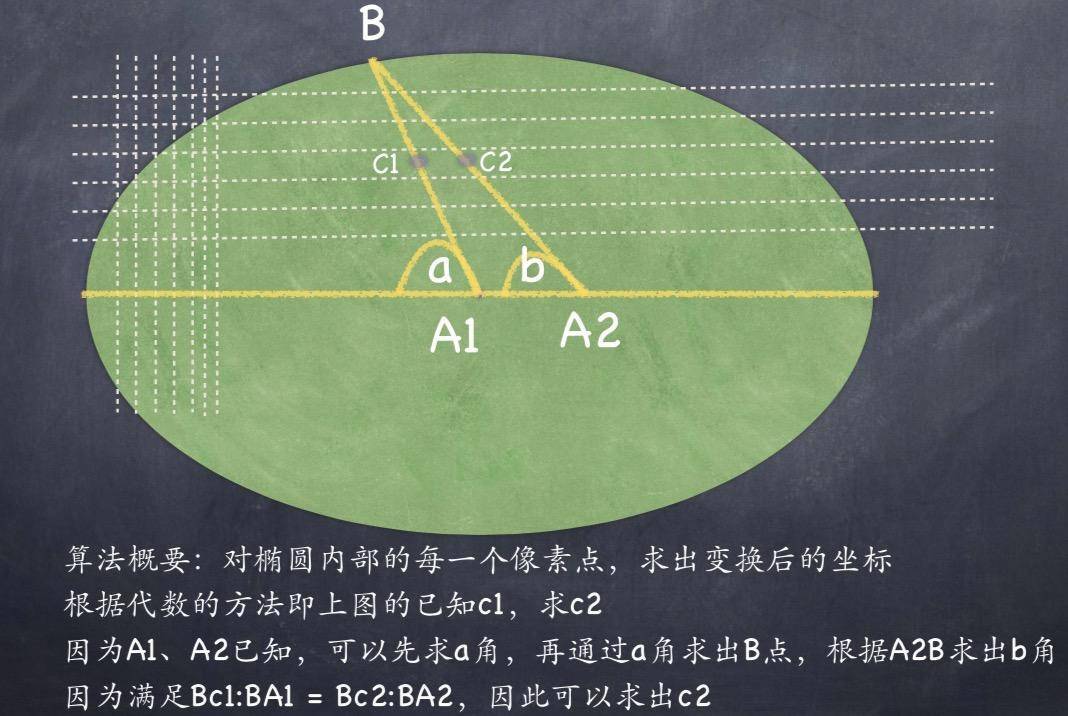
代数方法虽然能解决问题,但是会有4个缺陷:
不过,在我采用了向量法进行优化之后,这个动图的性能提升了数倍。具体算法如下图:
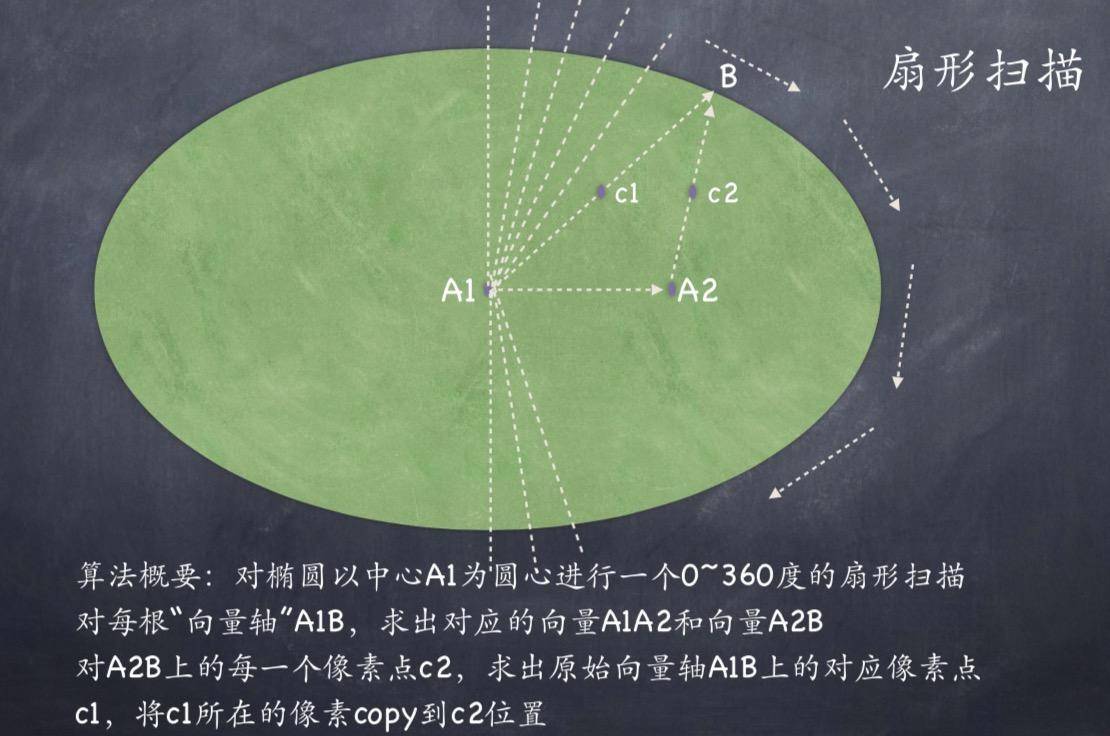
这两个案例其实共同说明一个道理:学会选择合适的数学工具,才能用最优的方式轻松解决问题。
以上就是我和数学相关的个人经历了。总的来说,我收获到最重要的经验就是,要学会选择合适的数学工具来解决问题。当你选对工具之后,那些看似复杂的问题,可能会变得无比简单,从而被迅速解决。所以我们要重视数学基础的积累,锻炼自己的数感,拓宽知识面,以数学思维来思考计算机问题。
当然,我也不是说,程序员必须要有多么高深的数学知识。你看我们专栏中需要的数学知识,基本上就是一些高中数学知识和一部分基础的线性代数知识。但是数感、数学思维锻炼还是很重要的,这些锻炼越多,程序员的逻辑能力、抽象能力也会得到提高。更重要的是,通过锻炼我们能形成用数学思维思考问题的习惯,这样才能迅速找到最合适解决某类问题的数学工具,从而提升我们的技术能力。
最后我再留两道思考题,来锻炼一下你的数感和数学思维能力。
欢迎你在留言说说数学对你的影响,也欢迎你和我分享关于数学方面的疑惑,我们一起探讨。