你好,我是Chrono。
在第26讲里,我介绍了TLS 1.2的握手过程,在Client Hello和Server Hello里用到了ECDHE算法做密钥交换,参数完全公开,但却能够防止黑客攻击,算出只有通信双方才能知道的秘密Pre-Master。
这是TLS握手的关键步骤,也让很多同学不太理解,“为什么数据都是不保密的,但中间人却无法破解呢?”
解答这个问题必须要涉及密码学,我原本觉得有点太深了,不想展开细讲,但后来发现大家都对这个很关心,有点“打破砂锅问到底”的精神。所以,这次我就试着从底层来解释一下。不过你要有点心理准备,这不是那么好懂的。
先从ECDHE算法的名字说起。ECDHE就是“短暂-椭圆曲线-迪菲-赫尔曼”算法(ephemeral Elliptic Curve Diffie–Hellman),里面的关键字是“短暂”“椭圆曲线”和“迪菲-赫尔曼”,我先来讲“迪菲-赫尔曼”,也就是DH算法。
DH算法是一种非对称加密算法,只能用于密钥交换,它的数学基础是“离散对数”(Discrete logarithm)。
那么,什么是离散对数呢?
上中学的时候我们都学过初等代数,知道指数和对数,指数就是幂运算,对数是指数的逆运算,是已知底数和真数(幂结果),反推出指数。
例如,如果以10作为底数,那么指数运算是y=10^x,对数运算是y=logx,100的对数是2(10^2=100,log100=2),2的对数是0.301(log2≈0.301)。
对数运算的域是实数,取值是连续的,而“离散对数”顾名思义,取值是不连续的,数值都是整数,但运算具有与实数对数相似的性质。
离散对数里的一个核心操作是模运算,也就是取余数(mod,在C、Java、Lua等语言里的操作符是“%”)。
假设有模数17,底数5,那么“5的3次方再对17取余数得6”(5 ^ 3 % 17 = 6)就是在离散整数域上的一次指数运算(5 ^ 3 (mod 17) = 6)。反过来,以5为底,17为模数,6的离散对数就是3(Ind(5, 6) = 3 ( mod 17))。
这里的(17,5)是离散对数的公共参数,6是真数,3是对数。知道了对数,就可以用幂运算很容易地得到真数,但反过来,知道真数却很难推断出对数,于是就形成了一个“单向函数”。
在这个例子里,选择的模数17很小,使用穷举法从1到17暴力破解也能够计算得到6的离散对数是3。
但如果我们选择的是一个非常非常大的数,比如说是有1024位的超大素数,那么暴力破解的成本就非常高了,几乎没有什么有效的方法能够快速计算出离散对数,这就是DH算法的数学基础。
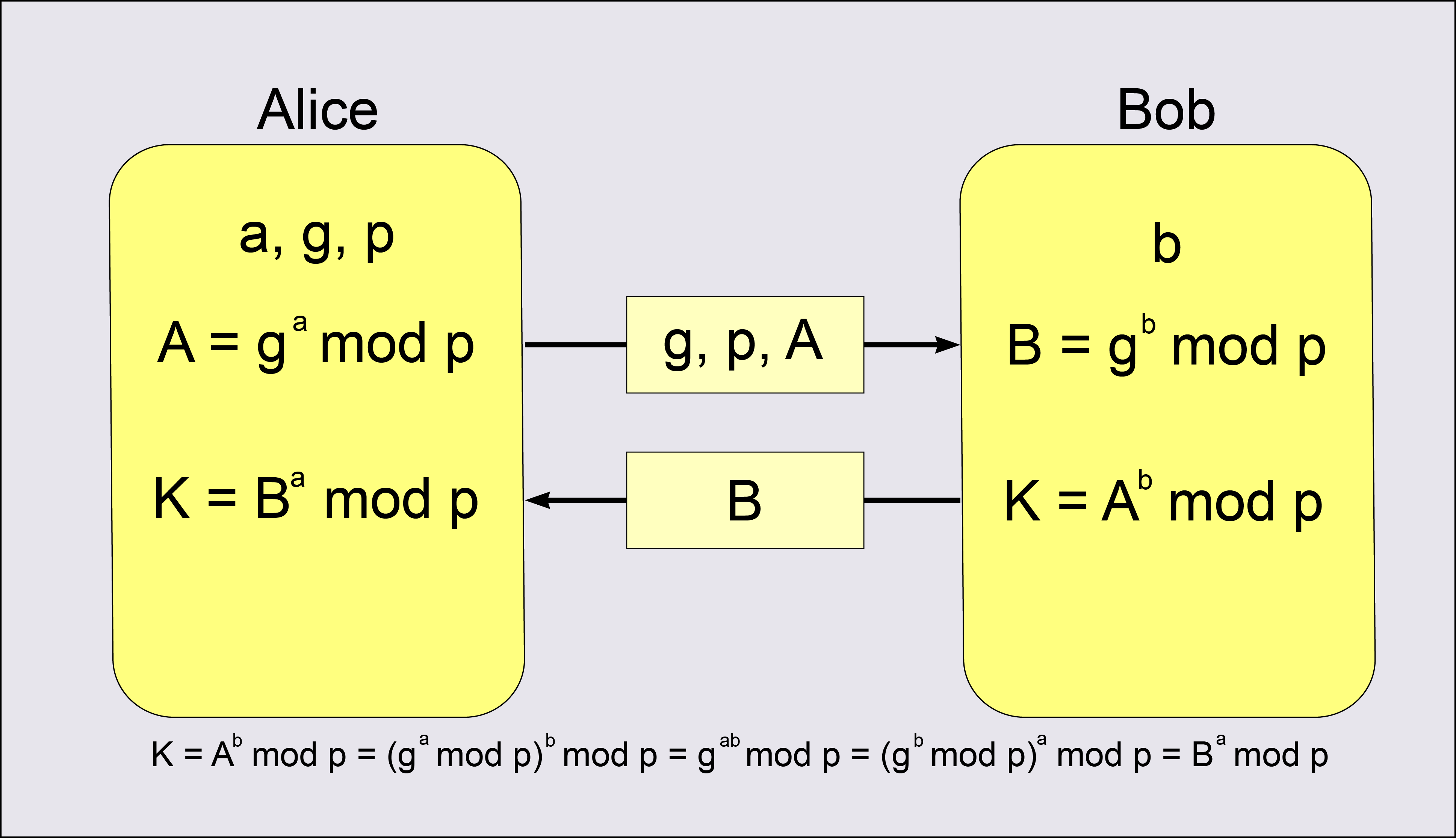
知道了离散对数,我们来看DH算法,假设Alice和Bob约定使用DH算法来交换密钥。
基于离散对数,Alice和Bob需要首先确定模数和底数作为算法的参数,这两个参数是公开的,用P和G来代称,简单起见我们还是用17和5(P=17,G=5)。
然后Alice和Bob各自选择一个随机整数作为私钥(必须在1和P-2之间),严格保密。比如Alice选择a=10,Bob选择b=5。
有了DH的私钥,Alice和Bob再计算幂作为公钥,也就是A = (G ^ a % P) = 9,B = (G ^ b % P) = 14,这里的A和B完全可以公开,因为根据离散对数的原理,从真数反向计算对数a和b是非常困难的。
交换DH公钥之后,Alice手里有五个数:P=17,G=5,a=10,A=9,B=14,然后执行一个运算:(B ^ a % P)= 8。
因为离散对数的幂运算有交换律,B ^ a = (G ^ b ) ^ a = (G ^ a) ^ b = A ^ b,所以Bob计算A ^ b % P也会得到同样的结果8,这个就是Alice和Bob之间的共享秘密,可以作为会话密钥使用,也就是TLS里的Pre-Master。

那么黑客在这个密钥交换的通信过程中能否实现攻击呢?
整个通信过程中,Alice和Bob公开了4个信息:P、G、A、B,其中P、G是算法的参数,A和B是公钥,而a、b是各自秘密保管的私钥,无法获取,所以黑客只能从已知的P、G、A、B下手,计算9或14的离散对数。
由离散对数的性质就可以知道,如果P非常大,那么他很难在短时间里破解出私钥a、b,所以Alice和Bob的通信是安全的(但在本例中数字小,计算难度很低)。
实验环境的URI“/42-1”演示了这个简单DH密钥交换过程,可以用浏览器直接访问,命令行下也可以用“resty www/lua/42-1.lua”直接运行。
DH算法有两种实现形式,一种是已经被废弃的DH算法,也叫static DH算法,另一种是现在常用的DHE算法(有时候也叫EDH)。
static DH算法里有一方的私钥是静态的,通常是服务器方固定,即a不变。而另一方(也就是客户端)随机选择私钥,即b采用随机数。
于是DH交换密钥时就只有客户端的公钥会变,而服务器公钥不变,在长期通信时就增加了被破解的风险,使得拥有海量计算资源的攻击者获得了足够的时间,最终能够暴力破解出服务器私钥,然后计算得到所有的共享秘密Pre-Master,不具有“前向安全”。
而DHE算法的关键在于“E”表示的临时性上(ephemeral),每次交换密钥时双方的私钥都是随机选择、临时生成的,用完就扔掉,下次通信不会再使用,相当于“一次一密”。
所以,即使攻击者破解了某一次的私钥,其他通信过程的私钥仍然是安全的,不会被解密,实现了“前向安全”。
现在如果你理解了DHE,那么理解ECDHE也就不那么困难了。
ECDHE算法,就是把DHE算法里整数域的离散对数,替换成了椭圆曲线上的离散对数。
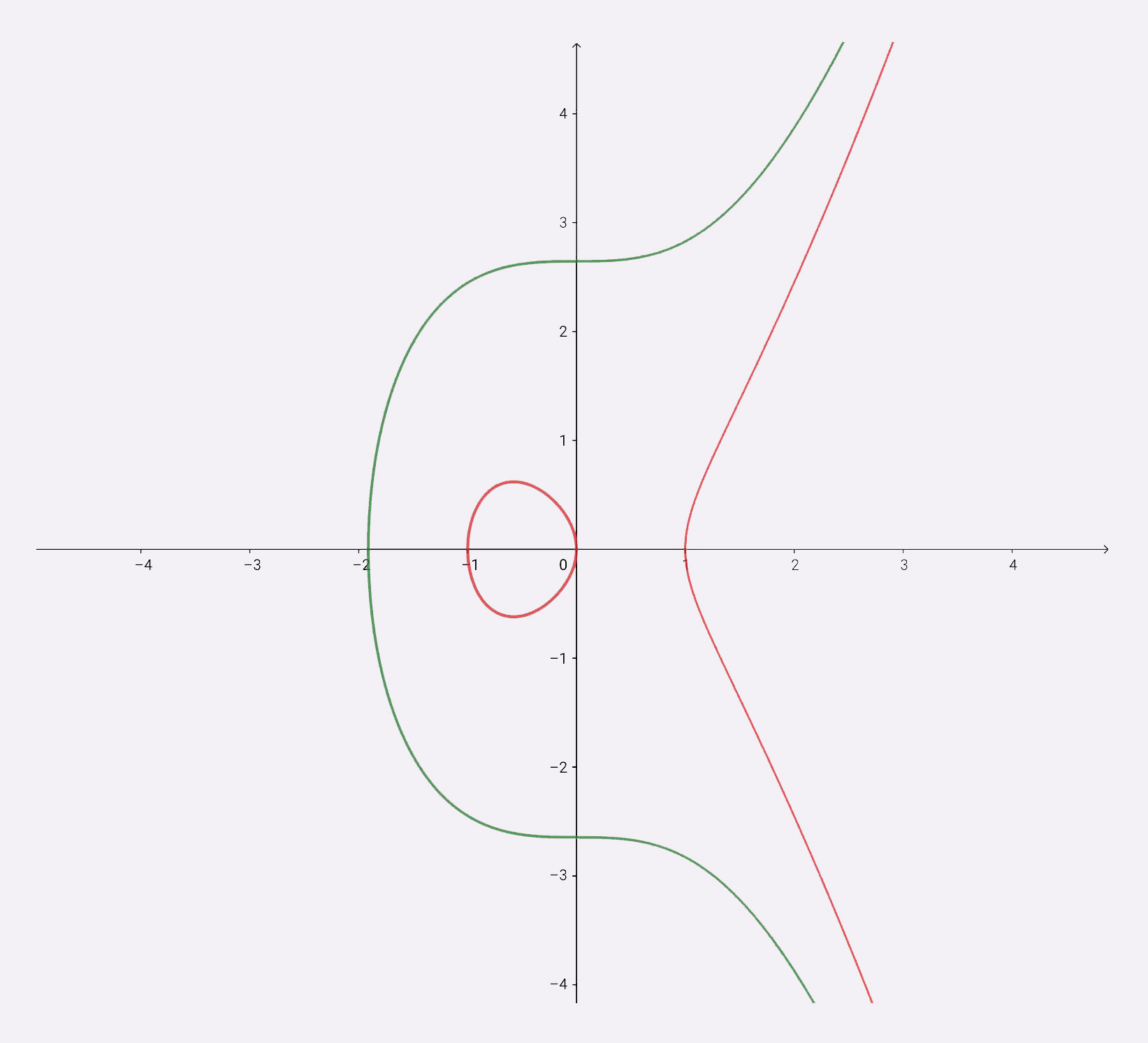
原来DHE算法里的是任意整数,而ECDHE则是把连续的椭圆曲线给“离散化”成整数,用椭圆曲线上的“倍运算”替换了DHE里的幂运算。
在ECDHE里,算法的公开参数是椭圆曲线C、基点G和模数P,私钥是倍数x,公钥是倍点xG,已知倍点xG要想计算出离散对数x是非常困难的。
在通信时Alice和Bob各自随机选择两个数字a和b作为私钥,计算A=aG、B=bG作为公钥,然后互相交换,用与DHE相同的算法,计算得到aB=abG=Ab,就是共享秘密Pre-Master。
因为椭圆曲线离散对数的计算难度比普通的离散对数更大,所以ECDHE的安全性比DHE还要高,更能够抵御黑客的攻击。
最后留一个思考题吧:为什么DH算法只能用于密钥交换,不能用于数字签名,如果你理解了DH算法的原理应该不难回答出来。
