
你好,我是winter,今天我们来学习一下CSS的动画和交互。
在CSS属性中,有这么一类属性,它负责的不是静态的展现,而是根据用户行为产生交互。这就是今天我们要讲的属性。
首先我们先从属性来讲起。CSS中跟动画相关的属性有两个:animation和transition。
我们先来看下animation的示例,通过示例来了解一下animation属性的基本用法:
@keyframes mykf
{
from {background: red;}
to {background: yellow;}
}
div
{
animation:mykf 5s infinite;
}
这里展示了animation的基本用法,实际上animation分成六个部分:
我们先来看 animation-name,这个是一个keyframes类型,需要配合@规则来使用。
比如,我们前面的示例中,就必须配合定义 mymove 这个 keyframes。keyframes的主体结构是一个名称和花括号中的定义,它按照百分比来规定数值,例如:
@keyframes mykf {
0% { top: 0; }
50% { top: 30px; }
75% { top: 10px; }
100% { top: 0; }
}
这里我们可以规定在开始时把top值设为0,在50%是设为30px,在75%时设为10px,到100%时重新设为0,这样,动画执行时就会按照我们指定的关键帧来变换数值。
这里,0%和100%可以写成from和to,不过一般不会混用,画风会变得很奇怪,比如:
@keyframes mykf {
from { top: 0; }
50% { top: 30px; }
75% { top: 10px; }
to { top: 0; }
}
这里关键帧之间,是使用 animation-timing-function 作为时间曲线的,稍后我会详细介绍时间曲线。
接下来我们来介绍一下transition。transition与animation相比来说,是简单得多的一个属性。
它有四个部分:
这里的四个部分,可以重复多次,指定多个属性的变换规则。
实际上,有时候我们会把transition和animation组合,抛弃animation的timing-function,以编排不同段用不同的曲线。
@keyframes mykf {
from { top: 0; transition:top ease}
50% { top: 30px;transition:top ease-in }
75% { top: 10px;transition:top ease-out }
to { top: 0; transition:top linear}
}
在这个例子中,在keyframes中定义了transition属性,以达到各段曲线都不同的效果。
接下来,我们就来详细讲讲刚才提到的timing-function,动画的时间曲线。
我想,你能从很多CSS的资料中都找到了贝塞尔曲线,但是为什么CSS的时间曲线要选用(三次)贝塞尔曲线呢?
我们在这里首先要了解一下贝塞尔曲线,贝塞尔曲线是一种插值曲线,它描述了两个点之间差值来形成连续的曲线形状的规则。
一个量(可以是任何矢量或者标量)从一个值到变化到另一个值,如果我们希望它按照一定时间平滑地过渡,就必须要对它进行插值。
最基本的情况,我们认为这个变化是按照时间均匀进行的,这个时候,我们称其为线性插值。而实际上,线性插值不大能满足我们的需要,因此数学上出现了很多其它的插值算法,其中贝塞尔插值法是非常典型的一种。它根据一些变换中的控制点来决定值与时间的关系。
贝塞尔曲线是一种被工业生产验证了很多年的曲线,它最大的特点就是“平滑”。时间曲线平滑,意味着较少突兀的变化,这是一般动画设计所追求的。
贝塞尔曲线用于建筑设计和工业设计都有很多年历史了,它最初的应用是汽车工业用贝塞尔曲线来设计车型。
K次贝塞尔插值算法需要k+1个控制点,最简单的一次贝塞尔插值就是线性插值,将时间表示为0到1的区间,一次贝塞尔插值公式是:

“二次贝塞尔插值”有3个控制点,相当于对P0和P1,P1和P2分别做贝塞尔插值,再对结果做一次贝塞尔插值计算
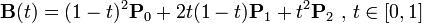
“三次贝塞尔插值”则是“两次‘二次贝塞尔插值’的结果,再做一次贝塞尔插值”:
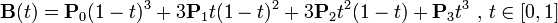
贝塞尔曲线的定义中带有一个参数t,但是这个t并非真正的时间,实际上贝塞尔曲线的一个点(x, y),这里的x轴才代表时间。
这就造成了一个问题,如果我们使用贝塞尔曲线的直接定义,是没办法直接根据时间来计算出数值的,因此,浏览器中一般都采用了数值算法,其中公认做有效的是牛顿积分,我们可以看下JavaScript版本的代码:
function generate(p1x, p1y, p2x, p2y) {
const ZERO_LIMIT = 1e-6;
// Calculate the polynomial coefficients,
// implicit first and last control points are (0,0) and (1,1).
const ax = 3 * p1x - 3 * p2x + 1;
const bx = 3 * p2x - 6 * p1x;
const cx = 3 * p1x;
const ay = 3 * p1y - 3 * p2y + 1;
const by = 3 * p2y - 6 * p1y;
const cy = 3 * p1y;
function sampleCurveDerivativeX(t) {
// `ax t^3 + bx t^2 + cx t' expanded using Horner 's rule.
return (3 * ax * t + 2 * bx) * t + cx;
}
function sampleCurveX(t) {
return ((ax * t + bx) * t + cx ) * t;
}
function sampleCurveY(t) {
return ((ay * t + by) * t + cy ) * t;
}
// Given an x value, find a parametric value it came from.
function solveCurveX(x) {
var t2 = x;
var derivative;
var x2;
// https://trac.webkit.org/browser/trunk/Source/WebCore/platform/animation
// First try a few iterations of Newton's method -- normally very fast.
// http://en.wikipedia.org/wiki/Newton's_method
for (let i = 0; i < 8; i++) {
// f(t)-x=0
x2 = sampleCurveX(t2) - x;
if (Math.abs(x2) < ZERO_LIMIT) {
return t2;
}
derivative = sampleCurveDerivativeX(t2);
// == 0, failure
/* istanbul ignore if */
if (Math.abs(derivative) < ZERO_LIMIT) {
break;
}
t2 -= x2 / derivative;
}
// Fall back to the bisection method for reliability.
// bisection
// http://en.wikipedia.org/wiki/Bisection_method
var t1 = 1;
/* istanbul ignore next */
var t0 = 0;
/* istanbul ignore next */
t2 = x;
/* istanbul ignore next */
while (t1 > t0) {
x2 = sampleCurveX(t2) - x;
if (Math.abs(x2) < ZERO_LIMIT) {
return t2;
}
if (x2 > 0) {
t1 = t2;
} else {
t0 = t2;
}
t2 = (t1 + t0) / 2;
}
// Failure
return t2;
}
function solve(x) {
return sampleCurveY(solveCurveX(x));
}
return solve;
}
这段代码其实完全翻译自WebKit的C++代码,牛顿积分的具体原理请参考相关数学著作,注释中也有相关的链接。
这个JavaScript版本的三次贝塞尔曲线可以用于实现跟CSS一模一样的动画。
理论上,贝塞尔曲线可以通过分段的方式拟合任意曲线,但是有一些特殊的曲线,是可以用贝塞尔曲线完美拟合的,比如抛物线。
这里我做了一个示例,用于模拟抛物线:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<meta name="viewport" content="width=device-width">
<title>Simulation</title>
<style>
.ball {
width:10px;
height:10px;
background-color:black;
border-radius:5px;
position:absolute;
left:0;
top:0;
transform:translateY(180px);
}
</style>
</head>
<body>
<label>运动时间:<input value="3.6" type="number" id="t" />s</label><br/>
<label>初速度:<input value="-21" type="number" id="vy" /> px/s</label><br/>
<label>水平速度:<input value="21" type="number" id="vx" /> px/s</label><br/>
<label>重力:<input value="10" type="number" id="g" /> px/s²</label><br/>
<button onclick="createBall()">来一个球</button>
</body>
</html>
function generateCubicBezier (v, g, t){
var a = v / g;
var b = t + v / g;
return [[(a / 3 + (a + b) / 3 - a) / (b - a), (a * a / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)],
[(b / 3 + (a + b) / 3 - a) / (b - a), (b * b / 3 + a * b * 2 / 3 - a * a) / (b * b - a * a)]];
}
function createBall() {
var ball = document.createElement("div");
var t = Number(document.getElementById("t").value);
var vx = Number(document.getElementById("vx").value);
var vy = Number(document.getElementById("vy").value);
var g = Number(document.getElementById("g").value);
ball.className = "ball";
document.body.appendChild(ball)
ball.style.transition = `left linear ${t}s, top cubic-bezier(${generateCubicBezier(vy, g, t)}) ${t}s`;
setTimeout(function(){
ball.style.left = `${vx * t}px`;
ball.style.top = `${vy * t + 0.5 * g * t * t}px`;
}, 100);
setTimeout(function(){ document.body.removeChild(ball); }, t * 1000);
}
这段代码中,我实现了抛物线运动的小球,其中核心代码就是 generateCubicBezier 函数。
这个公式完全来自于一篇论文,推理过程我也不清楚,但是不论如何,它确实能够用于模拟抛物线。
实际上,我们日常工作中,如果需要用贝塞尔曲线拟合任何曲线,都可以找到相应的论文,我们只要取它的结论即可。
我们今天的课程,重点介绍了动画和它背后的一些机制。
CSS用transition和animation两个属性来实现动画,这两个属性的基本用法很简单,我们今天还介绍了它们背后的原理:贝塞尔曲线。
我们中介绍了贝塞尔曲线的实现原理和贝塞尔曲线的拟合技巧。
最后,留给你一个小问题,请纯粹用JavaScript来实现一个transition函数,用它来跟CSS的transition来做一下对比,看看有哪些区别。
评论