你好，我是朱维刚。欢迎你跟我一起重学线性代数！

在开篇词中，我和你大致讲过我自己的经历，从2006年开始到现在14年的时间里，我都专注于机器学习领域。对于线性代数在机器学习中的应用，我非常了解。而这也是线性代数最主要的应用场景之一。因此，今天第一节课，我想先和你聊一聊，如何在机器学习中运用线性代数工具，在我们开始自下而上的学习之前，先从上层来看一看。

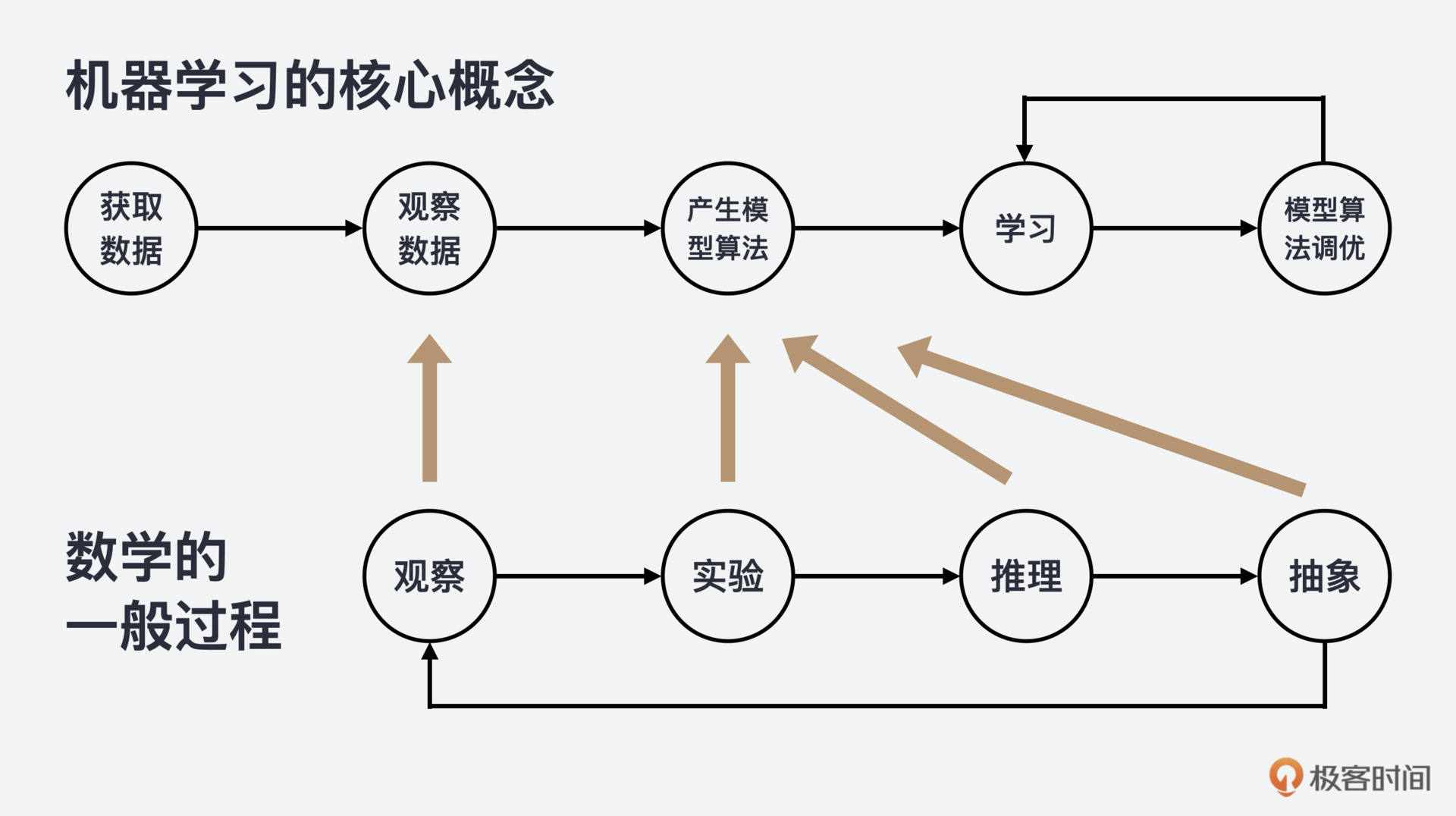
我们都知道，“数据”是机器学习的前提，机器学习的第一步就是要进行数据的收集、预处理和特征提取；而模型就是通过数据来学习的算法；学习则是一个循环过程，一个自动在数据中寻找模式，并不停调优模型参数的过程。那我们就从机器学习的三个核心概念：数据、模型和学习说起。

你看，不论是模型，还是学习，都涉及数据，而数据加上模型和学习，就是数学的一般过程了，也就是：观察、实验、推理和抽象。所以，我认为学好数学，不仅有利于理解复杂的机器学习系统，还能调优算法参数，甚至能帮助你创建新的机器学习解决方案。

从机器学习到线性代数

那机器学习和线性代数之间到底有着怎样的关系呢？我想，用一个实际的机器学习算法的例子来解释，你可能更容易搞清楚。接下来，我使用KNN（K-Nearest Neighbor，K最近邻分类算法）来让你简单了解一下机器学习，以及它和线性代数之间的关系。

之所以选KNN分类算法，因为它是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。这个方法的思路是：如果一个样本在特征空间中的K个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

这里有个前提，KNN算法中，所选择的“邻居”都是已经正确分类的对象。KNN分类算法在分类决策上只依据最邻近的一个或者几个样本的类别，来决定待分样本所属的类别。我们通过图来理解的话或许更容易一些。

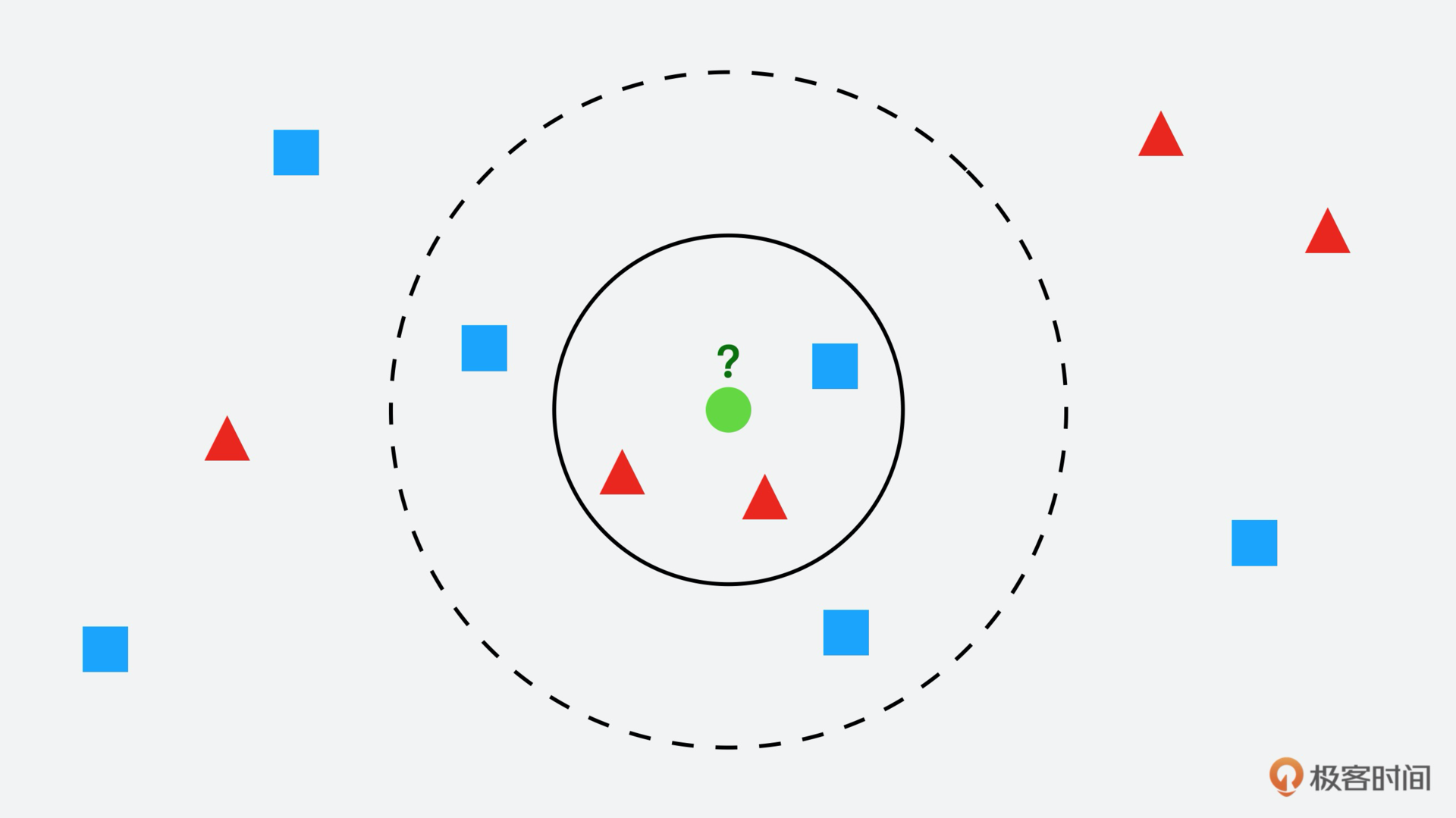
假设图片中那个绿色圆就要是我们要决策的对象，那么根据KNN算法它属于哪一类？是红色三角形还是蓝色四方形？

如果K=3（实线圆），也就是包含离绿色圆最近的3个，由于红色三角形所占比例为2/3，绿色圆就属于红色三角形那个类。但如果K=5（虚线圆），就是包含离绿色圆最近的5个，由于蓝色四方形比例为3/5，绿色圆就属于蓝色四方形那个类。

鸢尾花分类问题中的线性代数

通过前面这个小例子，你应该已经理解了KNN算法的概念。那么接下来，我们就试着使用KNN在给定鸢尾花特征值的情况下，给鸢尾花做花种分类，带你来实际看一下线性代数在这里起到的作用。

特别说明一下，鸢尾花分类问题是一个国际上通用的案例，一般都被作为机器学习入门来使用，所以它的数据集也是公开的。

1.数据集的收集、加载和分析

首先，我们要做的是数据集的收集、加载和分析，你也可以点击这里下载原始数据集，来看看原始数据长什么样，下面是获取和加载数据的代码，sklearn数据集已经包含了样本数据，你可以直接用。

import pandas as pd

from sklearn import datasets
iris = datasets.load_iris()

species = [iris.target_names[x] for x in iris.target]

iris = pd.DataFrame(iris['data'], columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])

iris['Species'] = species

从显示的结果，我们能够看出鸢尾花有四个特征：花萼的长、宽和花瓣的长、宽。我们来看下这四个特征的数据类型：

iris.dtypes
Sepal_Length    float64
Sepal_Width     float64
Petal_Length    float64
Petal_Width     float64
Species          object
dtype: object

这些特征都是数值型，而且标签Species表示的是花种，是一个字符串类型的变量。我们继续看一下鸢尾花的分类统计：

iris['count'] = 1
iris[['Species', 'count']].groupby('Species').count()

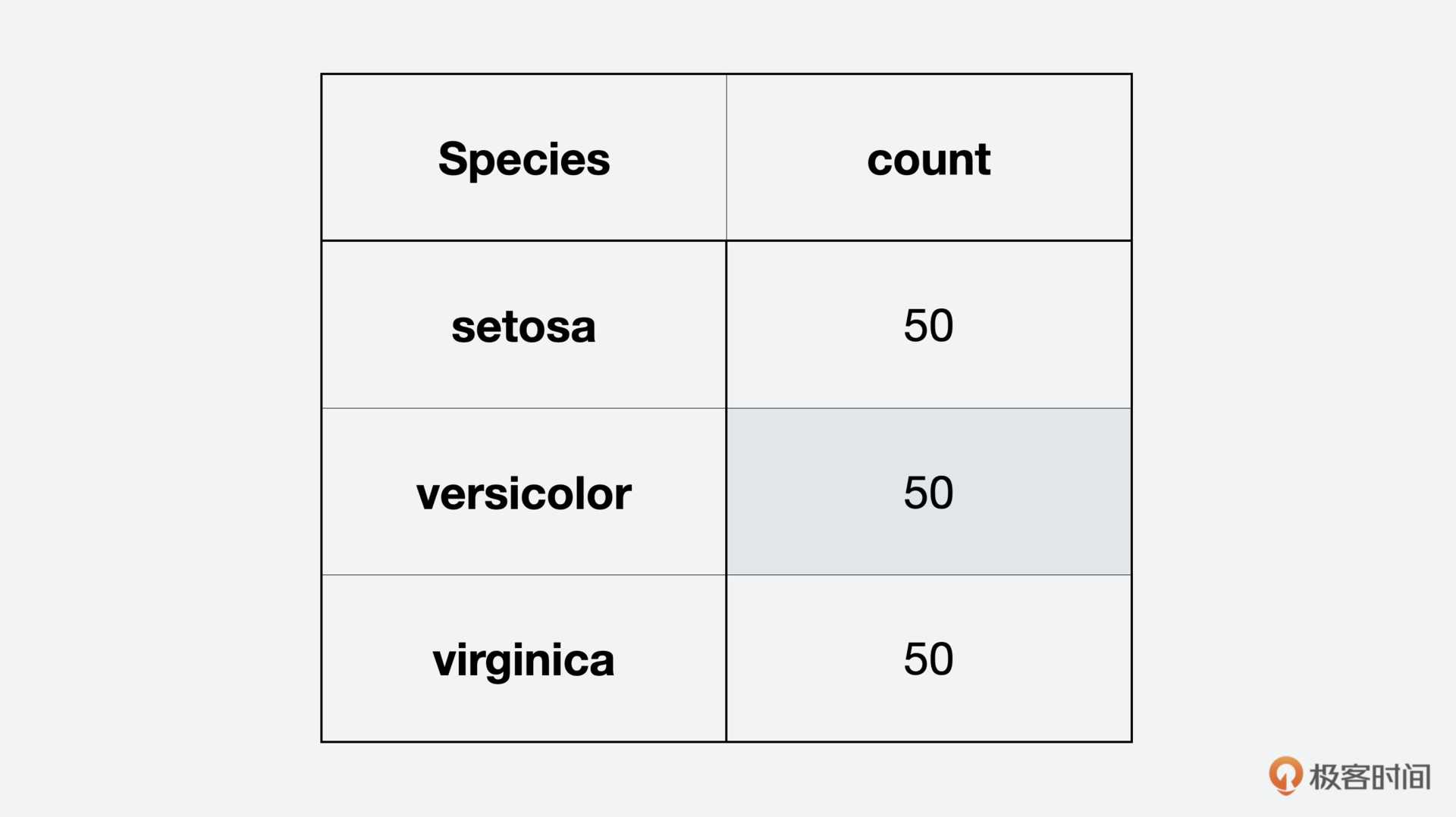
这里我们直接能够看到，鸢尾花有三个花种，每个种类有50个实例，或者说50条数据，我们再用图来更直观地显示这三种鸢尾花。

%matplotlib inline

def plot_iris(iris, col1, col2):
    import seaborn as sns
    import matplotlib.pyplot as plt

    sns.lmplot(x = col1, y = col2,
               data = iris,
               hue = "Species",
               fit_reg = False)

    plt.xlabel(col1)

    plt.ylabel(col2)

    plt.title('Iris species shown by color')

    plt.show()

plot_iris(iris, 'Petal_Width', 'Sepal_Length')

plot_iris(iris, 'Sepal_Width', 'Sepal_Length')

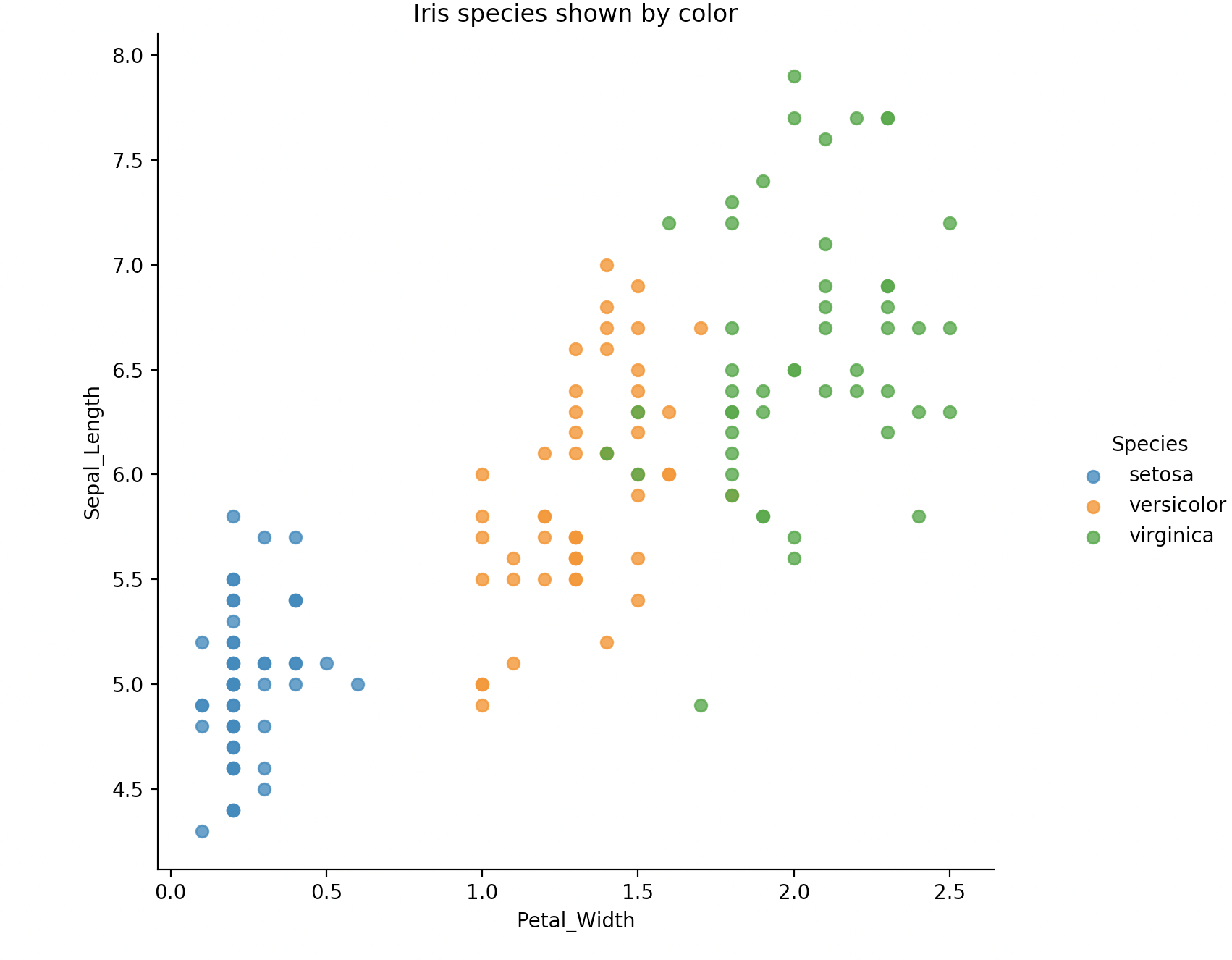
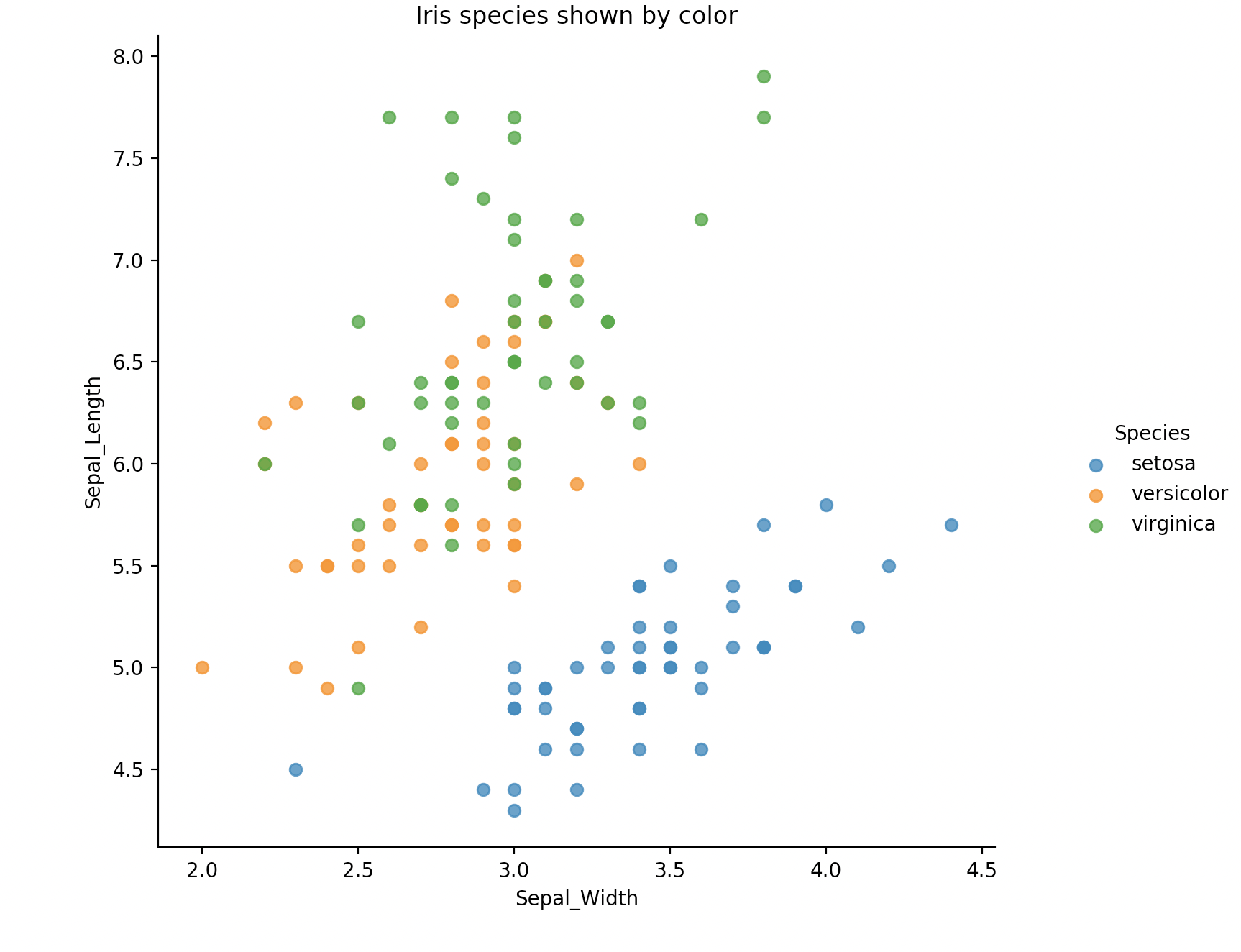
蓝、黄、绿，这三种颜色分别代表了三种鸢尾花，显示还是很清楚的。

2.数据集的准备

接下来的第二步就是数据集的准备了。在训练任何机器学习模型前，数据准备都相当重要，这里也要涉及两步准备。

第一步，特征数值标准化。如果我们不做标准化，后果就是大数值特征会主宰模型训练，这会导致更有意义的小数值特征被忽略。这里我们用Z Score标准化，使每一类特征平均值为0，方差为1.0，我们可以通过代码实现来看下效果。

from sklearn.preprocessing import scale

import pandas as pd

num_cols = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width']

iris_scaled = scale(iris[num_cols])

iris_scaled = pd.DataFrame(iris_scaled, columns = num_cols)

print(iris_scaled.describe().round(3))

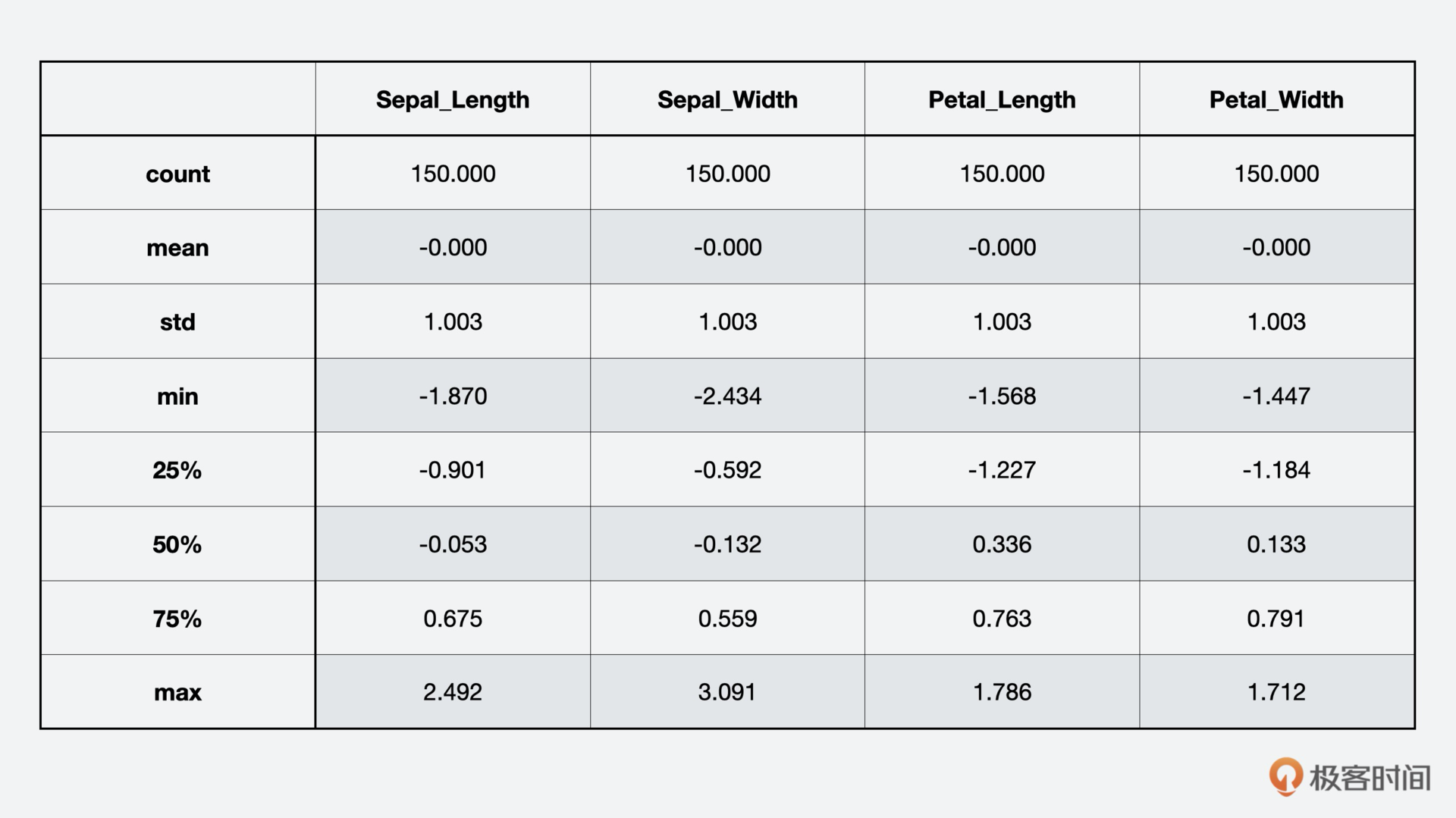
你可以看到，每一列平均值为0，标准差大约是1.0。为了分类需要，我们用字典把花种从字符串类型转换成数字表示。

levels = {'setosa':0, 'versicolor':1, 'virginica':2}

iris_scaled['Species'] = [levels[x] for x in iris['Species']]

iris_scaled.head()

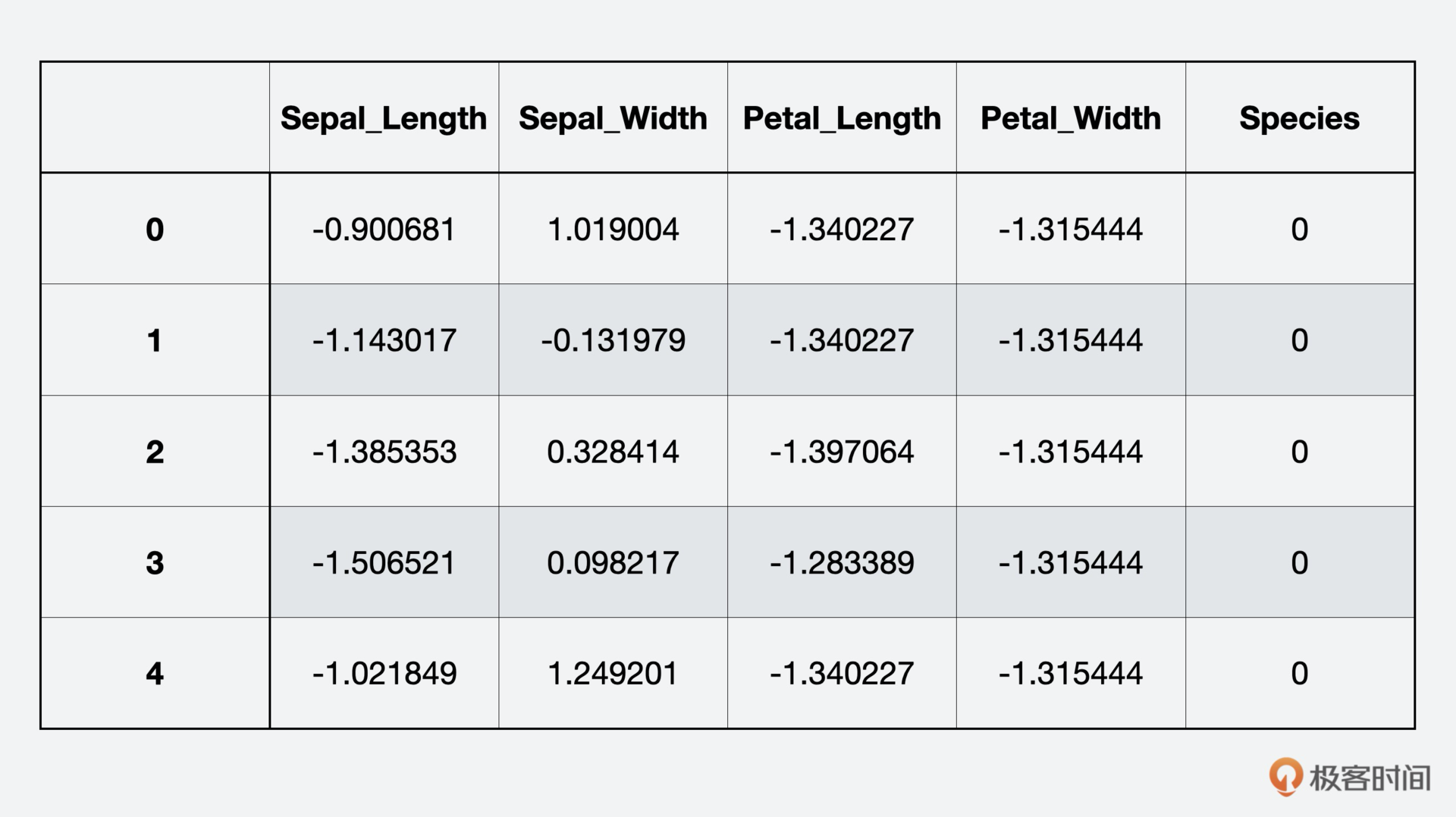
第二步，把数据集随机分割成样本训练集和评估数据集，训练集用来训练KNN模型，评估集用来测试和评估KNN的分类结果。

from sklearn.model_selection import train_test_split

import numpy as np

np.random.seed(3456)

iris_split = train_test_split(np.asmatrix(iris_scaled), test_size = 75)

iris_train_features = iris_split[0][:, :4]

iris_train_labels = np.ravel(iris_split[0][:, 4])

iris_test_features = iris_split[1][:, :4]

iris_test_labels = np.ravel(iris_split[1][:, 4])

print(iris_train_features.shape)

print(iris_train_labels.shape)

print(iris_test_features.shape)

print(iris_test_labels.shape)

通过代码，我们得到了下面这样的结果。

(75, 4)
(75,)
(75, 4)
(75,)

3.训练模型

数据准备好后，就是第三步训练模型了。这里我们使用K=3来训练KNN模型，当然你也可以调整这个参数来进行观察和调优。

from sklearn.neighbors import KNeighborsClassifier

KNN_mod = KNeighborsClassifier(n_neighbors = 3)

KNN_mod.fit(iris_train_features, iris_train_labels)

4.模型测试

执行KNN训练后，我们来到了最后一步，模型测试，这里我们使用测试集来测试模型。

iris_test = pd.DataFrame(iris_test_features, columns = num_cols)

iris_test['predicted'] = KNN_mod.predict(iris_test_features)

iris_test['correct'] = [1 if x == z else 0 for x, z in zip(iris_test['predicted'], iris_test_labels)]

accuracy = 100.0 * float(sum(iris_test['correct'])) / float(iris_test.shape[0])

print(accuracy)

96.0

最终，我们得到的准确率是96.0，说明了KNN的训练模型不错，适用这类场景。我们通过代码把其中的两个分类setosa和versicolor打印出来看看。

levels = {0:'setosa', 1:'versicolor', 2:'virginica'}

iris_test['Species'] = [levels[x] for x in iris_test['predicted']]

markers = {1:'^', 0:'o'}

colors = {'setosa':'blue', 'versicolor':'green',}

def plot_shapes(df, col1,col2,  markers, colors):
    import matplotlib.pyplot as plt
    import seaborn as sns

    ax = plt.figure(figsize=(6, 6)).gca() # define plot axis

    for m in markers: # iterate over marker dictioary keys
        for c in colors: # iterate over color dictionary keys
            df_temp = df[(df['correct'] == m)  & (df['Species'] == c)]
            sns.regplot(x = col1, y = col2,
                        data = df_temp, 
                        fit_reg = False,
                        scatter_kws={'color': colors[c]},
                        marker = markers[m],
                        ax = ax)
    plt.xlabel(col1)
    plt.ylabel(col2)
    plt.title('Iris species by color')
    return 'Done'

plot_shapes(iris_test, 'Petal_Width', 'Sepal_Length', markers, colors)
plot_shapes(iris_test, 'Sepal_Width', 'Sepal_Length', markers, colors)

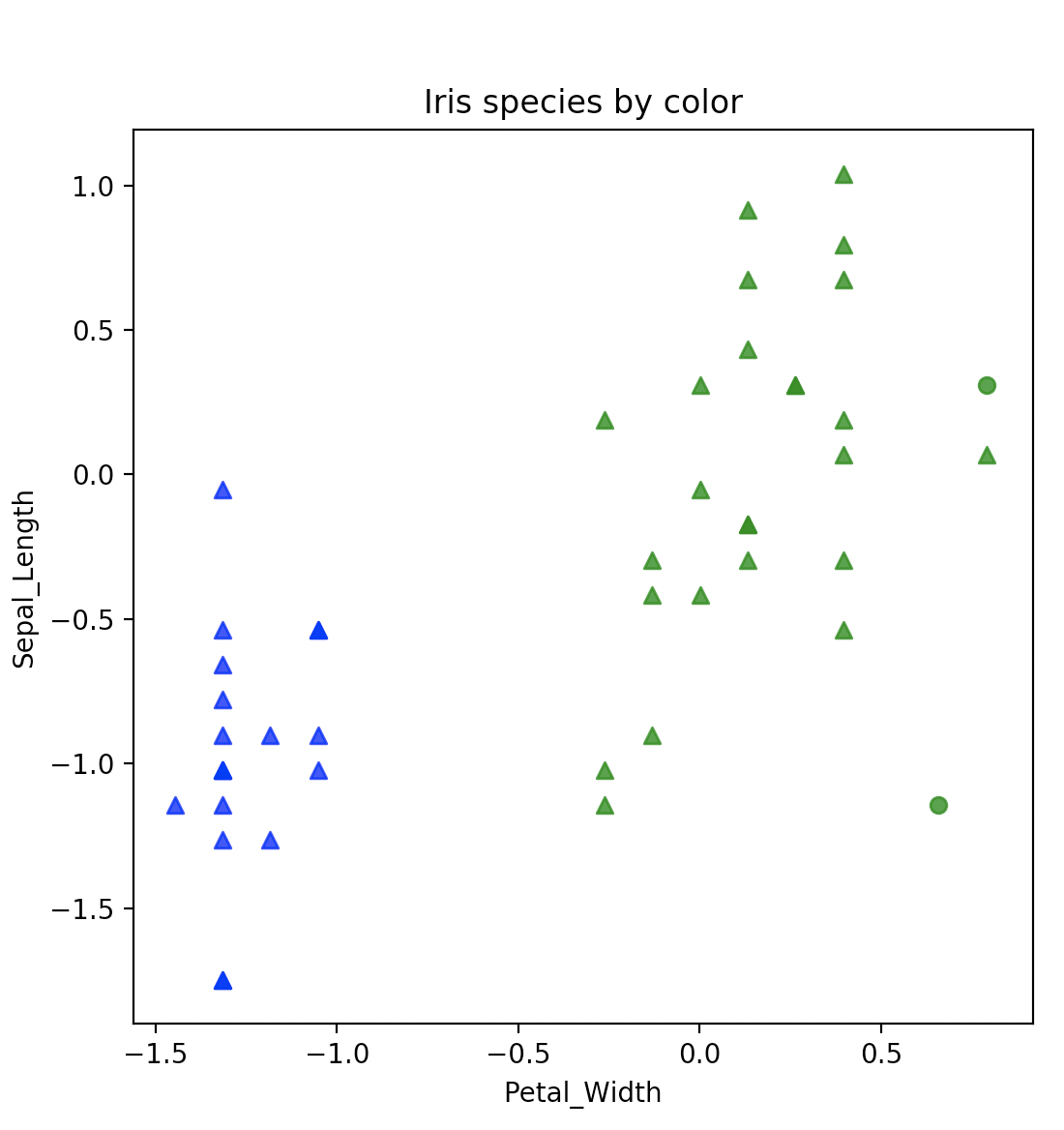
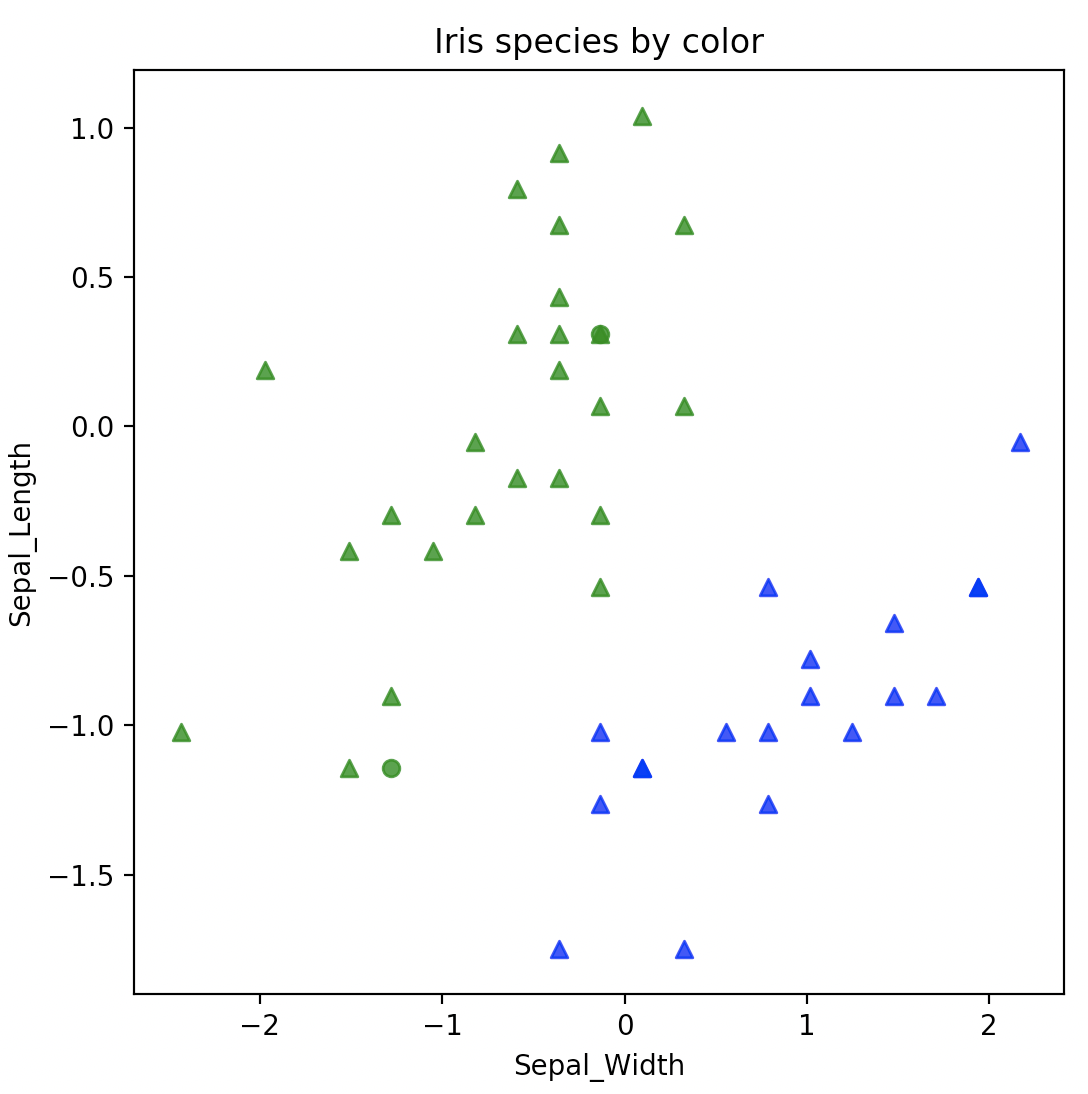
从显示的效果来说，分类还是挺明显的，熟悉了最基础的机器学习过程后，你可能会问，讲了半天，线性代数到底在哪里呢？关键就在KNeighborsClassifier模块上，这个模型算法的实现背后，其实用到了线性代数的核心原理。

首先，因为每种鸢尾花都有四个特征：花萼的长、宽和花瓣的长、宽，所以每条数据都是四维向量。

接着，量化样本之间的相似度，也就是计算向量之间的距离。而向量之间距离的运算有很多方式，比如：曼哈顿距离、欧式距离、切比雪夫距离、闵可夫斯基距离等等。其中，欧式距离你应该很熟悉了，因为我们初中都学过，在二维平面上计算两点之间的距离公式：

$$d=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}}$$

扩展到我们实例中的四维向量，也是同样的算法。

你看，这就是线性代数在机器学习中的一种应用场景。KNN是一种监督学习算法，因为在样本集中有分类信息，通过计算距离来衡量样本之间相似度，算法简单，易于理解和实现。还有另一种机器学习算法是无监督学习，底层的数学原理其实也是差不多的，总的思想就是“物以类聚”。

现在，你是不是有一种豁然开朗的感觉？终于看到了线性代数原来那么有意义，而且再简单的公式也是美的。

本节小结

好了，到这里导读这一讲就结束了，最后我再总结一下前面讲解的内容。

这一讲我使用机器学习的监督学习算法KNN，在给定鸢尾花特征值的情况下，给鸢尾花做花种分类，让你了解机器学习最基本的过程外，能够真正了解其背后的线性代数真相，为你进入后面课程的学习提供一个感性的认知。

机器学习中用到的线性代数知识点比比皆是，而且往往软件架构上看上去复杂的事情，在数学上反而很简单，希望你在学习了这门课程后，能够多从数学角度出发去构思解决问题的方案。

同时，欢迎你在留言区说说自己对机器学习的理解，也可以分享一下自己的线性代数学习经历，如果你有所收获，也欢迎你把这篇文章分享给你的朋友。