你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“线性无关”。
上一节课中,我讲的是线性空间的基本概念,是立足于宏观角度来讲的。那么今天,我们就要深入线性空间,从微观角度,再来看看线性空间中元素之间的关系,也就是线性组合。
线性组合有线性相关和线性无关,而线性无关是线性代数中最重要的概念之一,为什么这么说呢?因为线性相关的向量组中存在多余的向量,去掉它们不影响我们所考虑的问题。而线性无关向量集合是没有任何冗余的,也就是说,失去集合中任意一个向量,我们都会失去一些东西。接下来我们就开始把这个“直观上的理解”固化成实实在在的知识体系。
在正式开始讲解前,我还是一样,先通过一个例子,让你对线性组合有个大致的了解。
假设,有一家物流运输公司$Y$,$Y$主要靠车辆的货物运输来赚钱,而且$Y$拥有很多直营的运输车辆,设共有$n$辆车,${x_{1}, x_{2}, \ldots, x_{n}}$,那么,$Y$公司的收入可以表示成:$Y_{i}=a_{0}+a_{1} x_{1}+a_{2} x_{2}+\cdots+a_{n} x_{n}$。
这是个线性方程,它的系数$a$表示了各辆车对收入的贡献率,$a_{0}$表示企业的日常总支出。这时企业内,任何一辆车对收入的贡献大小和这个企业其他的车都没有关系,所以各车之间就是线性无关的。如果这时,我们再聚焦到每辆车本身的利润上,比如我们都知道的这个公式:利润=收入-成本,那每辆车的利润、成本和收入之间就是线性相关的。
在例子中,我们已经知道了线性组合中的线性相关、线性无关的意思。那么接下来,我们来看线性组合的确切定义:一个向量空间$V$和属于这个向量空间的有限数量的向量${x_{1}, x_{2}, \ldots, x_{k}}$,对于属于向量空间$V$的每个向量$v$,都有这样的表达形式:$v=\lambda_{1} x_{1}+\lambda_{2} x_{2}+\cdots+\lambda_{k} x_{k}=\sum_{i=1}^{k} \lambda_{i} x_{i}$。
那么,$v$就是向量${x_{1}, x_{2}, \ldots, x_{k}}$的线性组合。
我们继续看线性相关和线性无关的定义,一个向量空间$V$和属于这个向量空间的有限数量的向量${x_{1}, x_{2}, \ldots, x_{k}}$,有一个非平凡线性组合:$0=\lambda_{1} x_{1}+\lambda_{2} x_{2}+\cdots+\lambda_{k} x_{k}=\sum_{i=1}^{k} \lambda_{i} x_{i}$。如果其中至少有一个$λ$不等于0,这时,向量${x_{1}, x_{2}, \ldots, x_{k}}$是线性相关的。而如果有平凡解存在,例如:$λ_{1}= \ldots=λ_{k}=0$,则向量${x_{1}, x_{2}, \ldots, x_{k}}$是线性无关的。
注意:这里有个数学用语“平凡解”,术语“平凡”经常用于结构非常简单的对象,一般来说,$Ax=0$中的零解,即$x=0$,就叫做平凡解。
现在,我们通过一个实际的例子来加深一下理解。
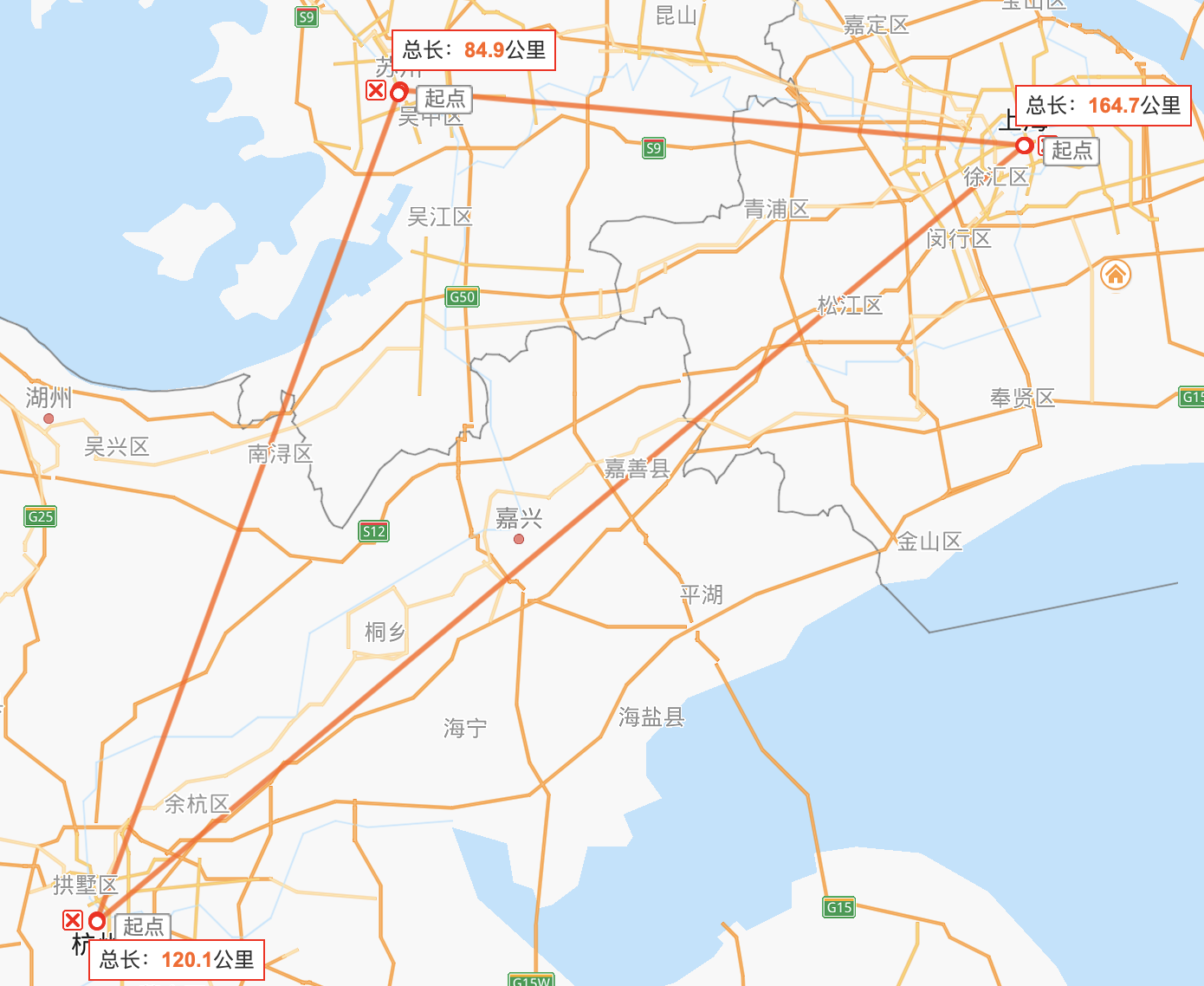
假如你想从上海去杭州,有两条路线可以供你选择:一条是从上海出发,行驶$84.9$公里后到苏州,再从苏州出发行驶$120.14$公里后到达杭州;另一条是从上海出发行驶$164.7$公里后直接到达杭州。

我们可以把地理位置坐标系看成是一个二维的向量空间,上海到苏州可以表示成向量$v1$,苏州到杭州可以表示成向量$v2$,上海到杭州可以表示成向量$v3$,这样很明显可以看出,向量$v1$和$v2$是线性无关的,而上海到杭州$v3$却可以被另两个向量$v1$和$v2$表达,于是我们可以说$v1$,$v2$和$v3$之间是线性相关的。
线性无关的判断,对于实践中数据冗余的判断非常有用,那有没有一些方法来判断向量之间是线性无关的呢?我们来看一些有用的方法吧:
之前的方式方法都是偏理论的,而更加实践的方法,就是用高斯消元法来判断向量集合${x_{1}, x_{2}, \ldots, x_{k}}$是否是线性无关的。将所有向量组合成矩阵的列,做高斯消元,一直到形成行阶梯型矩阵为止。如果所有的列都是主元列,那矩阵所有列向量是线性无关的,反之,如果有至少一个非主元列,那矩阵所有列向量是线性相关的。
现在我们来做个小练习,就用高斯消元法来看一下这3个向量是否是线性无关的。
$$x_{1}=\left[\begin{array}{c}
1 \\\
2 \\\
-3 \\\
4
\end{array}\right], x_{2}=\left[\begin{array}{l}
1 \\\
1 \\\
0 \\\
2
\end{array}\right], x_{3}=\left[\begin{array}{c}
-1 \\\
-2 \\\
1 \\\
1
\end{array}\right]$$
首先,我们把它表示成一般线性方程形式,或者一个非平凡线性组合。
$$\lambda_{1} x_{1}+\lambda_{2} x_{2}+\lambda_{3} x_{3}=\lambda_{1}\left[\begin{array}{c}
1 \\\
2 \\\
-3 \\\
4
\end{array}\right]+\lambda_{2}\left[\begin{array}{c}
1 \\\
1 \\\
0 \\\
2
\end{array}\right]+\lambda_{3}\left[\begin{array}{c}
-1 \\\
-2 \\\
1 \\\
1
\end{array}\right]=0$$
接着,把向量组合成矩阵的列,运用行运算,一直到能够识别出主元列为止。
$$\left[\begin{array}{ccc}
1 & 1 & -1 \\\
2 & 1 & -2 \\\
-3 & 0 & 1 \\\
4 & 2 & 1
\end{array}\right] \cdots\left[\begin{array}{ccc}
1 & 1 & -1 \\\
0 & 1 & 0 \\\
0 & 0 & 1 \\\
0 & 0 & 0
\end{array}\right]$$
这里,矩阵每一列都是主元列,所以,它没有非平凡解,只有在$λ_{1}=0$,$λ_{2}=0$,$λ_{3}=0$的情况下,方程才有解。因此,我们能说向量${x_{1}, x_{2}, x_{k}}$ 是线性无关的。
理论是这样的,接下来我们再扩展一下学到的知识,把它用到更普遍和复杂的情况中,也就是有$k$个线性无关的向量${b_{1}, b_{2}, \ldots, b_{k}}$,以及$m$个线性组合的情况:
$$
\begin{aligned}
x_{1} &=\sum_{i=1}^{k} \lambda_{i 1} b_{i} \\\
x_{2} &=\sum_{i=1}^{k} \lambda_{i 2} b_{i} \\\
\cdot & \\\
\cdot & \\\
\cdot & \\\
x_{m} &=\sum_{i=1}^{k} \lambda_{i m} b_{i}
\end{aligned}
$$
如果把这$k$个线性无关的向量组合成矩阵$B$,$B=\left[\begin{array}{lll}b_{1} & \ldots & b_{k}\end{array}\right]$ ,我们就能用更紧凑的形式来表达:
$$x_{j}=B \lambda_{i}, \lambda_{j}=\left[\begin{array}{c}
\lambda_{1 j} \\\
\cdot \\\
\cdot \\\
\cdot \\\
\lambda_{kj}
\end{array}\right], j=1, \ldots, m$$
这时,如何判断${x_{1}, x_{2}, \ldots, x_{m}}$ 是否是线性无关的呢?首先,我们用一个非平凡线性组合来测试,就和之前的方法一样,把它表示成这样的形式:$\sum_{i=1}^{m} \varphi_{j} x_{j}=\sum_{i=1}^{m} \varphi_{j} B \lambda_{j}=B \sum_{i=1}^{m} \varphi_{j} \lambda_{j}=0$。
接着,从这样的等式可以很容易看出,只有向量${λ_{1}, λ_{2}, \ldots, λ_{m}}$线性无关,${x_{1}, x_{2}, \ldots, x_{m}}$ 才是线性无关的。
还是老样子,我们通过一个例子来看下。假设,有一组线性无关的向量 ${b_{1}, b_{2}, b_{3}, b_{4}}$,和4个线性组合。
$$\left\{\begin{aligned}
x_{1} &=b_{1}-2 b_{2}+b_{3}-b_{4} \\\
x_{2} &=-4 b_{1}-2 b_{2}+4 b_{4} \\\
x_{3} &=2 b_{1}+3 b_{2}-b_{3}-3 b_{4} \\\
x_{4} &=17 b_{1}-10 b_{2}+11 b_{3}+b_{4}
\end{aligned}\right.$$
接下来我们该怎么判断${x_{1}, x_{2}, x_{3}, x_{4}}$是否是线性无关的呢?按刚才说的方法,我们需要首先找到$λ$向量,通过$λ$向量组合成这样的矩阵:
$$\left[\begin{array}{cccc}
1 & -4 & 2 & 17 \\\
-2 & -2 & 3 & -10 \\\
1 & 0 & -1 & 11 \\\
-1 & 4 & -3 & 1
\end{array}\right]$$
接着,使用高斯消元法,一直到形成行阶梯型矩阵为止。高斯消元法的用法已经在第四节课中详细说了,如果你有些记不清,可以回去复习一下。这里我们直接得到了行阶梯型矩阵:
$$
\left[\begin{array}{cccc}
1 & 0 & 0 & -7 \\\
0 & 1 & 0 & -15 \\\
0 & 0 & 1 & -18 \\\
0 & 0 & 0 & 0
\end{array}\right]
$$
矩阵的最后一列不是主元列,而且你可以很直观地发现 $x_{4}=-7 x_{1}-15 x_{2}-18 x_{3}$,所以,我们可以判断 ${x_{1}, x_{2}, x_{3}, x_{4}}$是线性相关的,$x_{4}$ 能由 ${x_{1}, x_{2}, x_{3}}$ 的线性组合来表达。
友情提醒:已知在一个向量空间$V$中,有$k$个向量 ${x_{1}, x_{2}, \ldots, x_{k}}$和$m$个线性组合,如果$m>k$,那么我们可以说,这$k$个向量 ${x_{1}, x_{2}, \ldots, x_{k}}$ 的$m$个线性组合是线性相关的。所以,在这样的情况下,就为你省去了计算的时间。
在了解了线性组合的概念,以及线性组合中的线性相关,特别是线性无关的判断后,我们来看一个机器学习中的实践例子,来了解一下线性组合是怎么体现在机器学习中的。
机器学习中,最经典,也是最简单的线性组合应用莫过于线性回归了。线性回归是比较常见,也是简单实用的机器学习算法,它是利用数理统计中的回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
线性回归假设目标值与特征之间线性相关,也就是说满足一个多元一次方程。它可以通过构建“损失(loss)”函数,来求解损失函数最小时的参数$w$和$b$,也就是说,整个机器学习的过程就是通过样本数据,得到最后的参数$w$和$b$。
我们通过一个例子来看看线性回归。
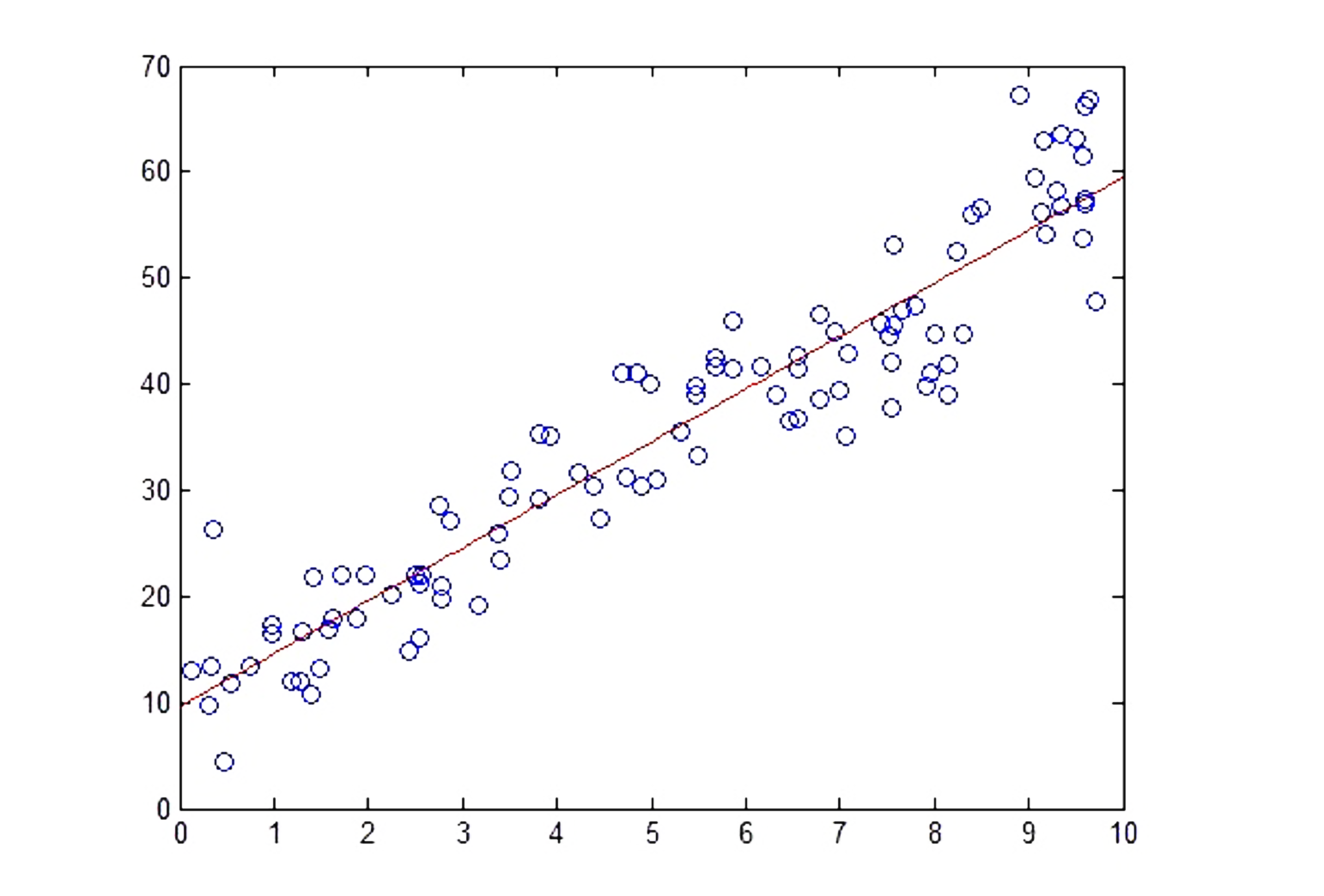
这是一个典型的一元线性回归模型。图中的空心圆点是真实数据点,而红线是一元线性回归模型,是用来做数据预测的,也就是$y=\omega^{T} x+b$。我们可以根据给定的$x$值通过方程式来计算$y$值。从分布在红色线周围的真实数据点来看,其实我们可以直观的得出结论:这个一元线性回归模型可以被用来很好的做预测。
线性回归在现实生活中的一个典型的应用场景是健身卡路里的燃烧预测,比如输入数据是年龄、性别、身高、体重、健身心跳、健身持久时间,而输出则是燃烧掉的卡路里。
怎么样?机器学习是不是很简单?
其实,机器学习的本质就是用数学来解决现实的问题。而很多看起来简单的数学公式可以解决很多问题,比如这里说的线性组合应用——线性回归。
我最近发现,有不少同学遇到问题,都想着怎么用复杂的机器学习算法去解决问题,特别是高大上的深度学习、神经网络之类的。但其实对于机器学习来说,算法不是越复杂越好,而是越适用越好。你可以先从简单的算法模型入手,先验证效果后,再做进一步的判断,是否需要用更复杂的算法模型。
好了,到这里线性无关这一讲就结束了,最后我再总结一下前面讲解的内容。
向量空间是实践的基本单位,之前都是从宏观角度出发的,而今天的知识的重点在于,我从微观角度,深入讲解了线性空间中元素之间的关系,也就是线性组合,线性组合有线性相关和线性无关,而线性无关是线性代数中最重要的概念之一。所以,你一定要掌握线性组合的概念,以及它包含的线性相关,特别是线性无关的判断方式,希望你能多练习线性组合中的线性无关的判断,为实践打好坚实的基础。
练习时刻到了,今天的练习题简单一些,和之前举过的例子相似,假设我们有一组线性无关的向量${b_{1}, b_{2}, b_{3}, b_{4}}$,和4个线性组合。
$$\left\{\begin{aligned}
x_{1} &=b_{1}+b_{2}-2 b_{3}-b_{4} \\\
x_{2} &=b_{1}+5 b_{2}-3 b_{3}-2 b_{4} \\\
x_{3} &=3 b_{1}-b_{2}+b_{3}+4 b_{4} \\\
x_{4} &=-2 b_{1}+2 b_{2}+b_{3}-b_{4}
\end{aligned}\right.$$
请你判断${x_{1}, x_{2}, x_{3}, x_{4}}$是线性无关的吗?
友情提示:通过高斯消元法,我们能得到行阶梯型矩阵,通过行阶梯型矩阵,就可以判断${x_{1}, x_{2}, x_{3}, x_{4}}$是否是线性无关的。
欢迎你在留言区或部落里晒出你的运算过程和结果。如果有收获,也欢迎你把这篇文章分享给你的朋友。
评论