你好，我是朱维刚。欢迎你继续跟我学习线性代数，今天我要讲的内容是“如何运用线性代数方法解决图论问题”。

“图”这个字在计算机科学领域很常见，特别是在数据结构中。一说到图，是必定要联系到图论（Graph Theory）的，因为它是以图为研究对象的数学的一个分支。图论中的图，是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用点代表事物，用连接两点的线表示相应两个事物间具有这种关系。

说到这，你也许会问，这个和线性代数、矩阵有什么关系？

图的数学定义

既然是数学课，我们还是要先讲一下图的数学定义：一个图$G$是指一个有序三元组$(V, E, \phi)$，$V$是非空的顶点集；$E$是不与$V$相交的边集；$\phi$是关联函数，它使$G$的每条边对应于$G$的无序顶点对。如果$e$是一条边，$u$和$v$是顶点，使得$\phi(e)=u v$，则$e$连接$u$和$v$，也就是顶点$u$和$v$是$e$的端点。

好了，现在是时候通过两个应用场景来看下，如何把矩阵和图论关联起来，并运用在解决实际问题中了。

邻接矩阵应用

首先，是邻接矩阵（Adjacency Matrix），邻接矩阵是表示顶点之间相邻关系的矩阵。假设$G$是一个图，$V(G)$是$G$的顶点集，$E(G)$是$G$的边集，设$G$中有$n$个顶点，$v_{1}, v_{2}, \ldots, v_{n}$，$A=(a_{ij})_{n×n}$是$G$的邻接矩阵。

$$a_{i}=\left\{\begin{array}{l}
1, v_{i} v_{j} \in E(G) \\\
0, v_{i} v_{j} \notin E(G)^{\prime}, i, j=1,2, \ldots, n
\end{array}\right.$$

已知情况是这样的，那我们现在来看一下邻接矩阵在现实问题中的应用。这个例子来源于1994年全国大学生数学建模竞赛试题B题。

某厂生产一种弹子锁具，每个锁具的钥匙有5个槽，每个槽的高度从$｛1,2,3,4,5,6｝$中任取一数。由于工艺及其他原因，制造锁具时对5个槽的高度还有两个限制。

至少有3个不同的数；
相邻两槽的高度之差不能为5。

满足以上条件制造出来的所有互不相同的锁具称为一批。销售部门在一批锁具中随意地取每60个装成一箱出售。问：每一批锁具有多少个，装多少箱？

我们先来看下弹子锁具的样子，否则自己想象会要一些时间。

这是一个7个槽的弹子锁具，只是比我们例子的5个槽多了两个槽。有了弹子锁具形象化输出后，我们开始解题。锁具装箱是一个排列组合的数学问题，但如果我们用图论的邻接矩阵方法来解这个问题，就能够起到化繁为简的作用。

首先，我们构造一个6节点的图：把1、2、3、4、5、6这6个数作为6个节点，如果两个数字可以相邻，那这两个节点之间就加一条边，每个节点有自己到自己的一条边。于是，我们得到了锁具各槽之间的关系图：

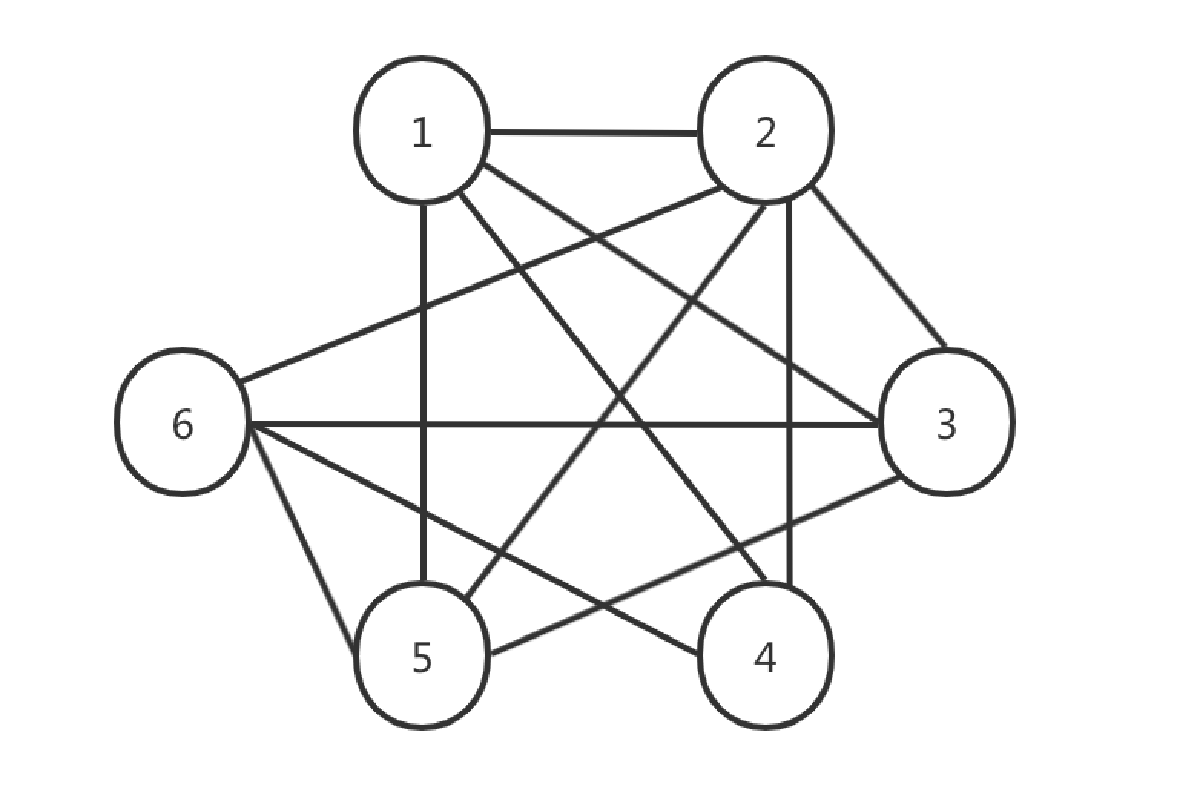
接着，构建邻接矩阵$A$，根据前面说的，如果两点之间有一条边，那在矩阵中，相应位置的值就是1，比如：节点1和2之间有一条边，那矩阵第一行第二列和第二行第一列的值就是1，节点1和6之间没有边，那矩阵第一行第六列和第六行第一列的值就是0，因为每个节点有自己到自己的一条边，所以第一行第一列的值就是1，其它5个节点也是一样的。

$$A=\left[\begin{array}{llllll}
1 & 1 & 1 & 1 & 1 & 0 \\\
1 & 1 & 1 & 1 & 1 & 1 \\\
1 & 1 & 1 & 1 & 1 & 1 \\\
1 & 1 & 1 & 1 & 1 & 1 \\\
1 & 1 & 1 & 1 & 1 & 1 \\\
0 & 1 & 1 & 1 & 1 & 1
\end{array}\right]$$

因为我们从没有1、6相邻的关系图得到了邻接矩阵$A$，所以$A$中所有元素之和表示两个槽高无1、6相邻的锁具个数。而每个无1、6相邻的5位数与关系图中长度是1的一条链一一对应。于是，$A^{k}$中各元素之和就是长度为$k$的链接个数。比如，$A^{2}$中第$i$行第$j$列的元素就是$i$开始经过两条边到达$j$的链接个数。我们这里因为是5个元素，也就是要经过4条边，所以需要计算$A^{4}$。

$$A^{4}=\left[\begin{array}{cccccc}
141 & 165 & 165 & 165 & 165 & 140 \\\
165 & 194 & 194 & 194 & 194 & 165 \\\
165 & 194 & 194 & 194 & 194 & 165 \\\
165 & 194 & 194 & 194 & 194 & 165 \\\
165 & 194 & 194 & 194 & 194 & 165 \\\
140 & 165 & 165 & 165 & 165 & 141
\end{array}\right]$$

把$A^{4}$中的元素求和，就能得到相邻高差为5的锁具数是6306。

最后，因为题目的限制提到了槽的高度至少有3个不同的数，我们还要把6306这个数字减去仅有一个、两个槽高的锁具：$6306-\left(6+\left(C_{6}^{2}-1\right)\left(2^{5}-2\right)\right)=5880$。

所以，我们得到一批锁具的个数是5880，总共装5880/60=98箱。

这样，我们通过邻接矩阵的图论知识，解决了一批锁具的数量问题，比其它方法看起来更简单。

特别提示：文中用到的$A^{k}$在图论中的实际意义，是来自刘亚国的一篇文献《图论中邻接矩阵的应用》。

关联矩阵应用

接下来，我们在邻接矩阵上再升级一下，把边变成有向边。这样就形成了另一类矩阵：关联矩阵。关联矩阵经常被用在图论中，现在我们就来看一下关联矩阵和图之间的关系。如下图所示，我们定义了一个拥有4个节点和6条边的图。

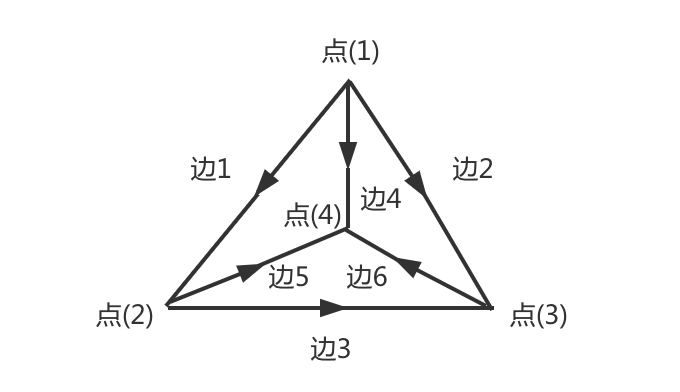
接下来，定义一个6×4的矩阵来描述这个图，其中列表示点(1)到点(4)，行表示边1到边6：

$$A=\left[\begin{array}{cccc}
-1 & 1 & 0 & 0 \\\
-1 & 0 & 1 & 0 \\\
0 & -1 & 1 & 0 \\\
-1 & 0 & 0 & 1 \\\
0 & -1 & 0 & 1 \\\
0 & 0 & -1 & 1
\end{array}\right]$$

矩阵$A$只包含了三类元素：-1、1、0。-1表示点的箭头的出方向，1表示点的箭头的入方向，0则表示点和点之间没有关联。举例来说，矩阵$A$的第一行元素是-1、1、0、0，那对于边1和点(1)、点(2)说，我们从图中可以看到边1是从点(1)到点(2)，$A$中-1对于点(1)来说是箭头的出方向，1对于点(2)来说是箭头的入方向，而边1和点(3)、点(4)没有任何关系，所以第一行第三列和第四列都是0。

这里，我们把关联矩阵用到现实场景中，比如：让它为电子电路服务，用它来分析整个电路的情况，也就是电路的拓扑结构，这里的电路指的是基尔霍夫定律，是分析和计算较为复杂电路的基础。假设$x_{1}, x_{2}, x_{3}, x_{4}$是这几个点的电压值，我们来看一下$Ax$的结果：

$$A x=\left[\begin{array}{cccc}
-1 & 1 & 0 & 0 \\\
-1 & 0 & 1 & 0 \\\
0 & -1 & 1 & 0 \\\
-1 & 0 & 0 & 1 \\\
0 & -1 & 0 & 1 \\\
0 & 0 & -1 & 1
\end{array}\right]\left[\begin{array}{l}
x_{1} \\\
x_{2} \\\
x_{3} \\\
x_{4}
\end{array}\right]=\left[\begin{array}{c}
x_{2}-x_{1} \\\
x_{3}-x_{1} \\\
x_{3}-x_{2} \\\
x_{4}-x_{1} \\\
x_{4}-x_{2} \\\
x_{4}-x_{3}
\end{array}\right]$$

由此可见，结果是差值，也就是沿着边1到6的电势差，有了电势差，就说明有电流，但如果Ax=0会怎样呢？也就是方程满足这样的等式：

很明显，这些差值，也就是电势差都等于0，意味着没有电流。同理，如果把电压值换成温度呢？那应用场景就切换成热传导了。

刚才我们看到了$Ax=0$的情况，你还记得第八篇中说的零空间吗？它关注的就是$Ax=0$，也就是向量空间$V$中所有经过$\phi$映射为零的向量集合，用符号表示就是：$ker(\phi)$，它的维数叫做零化度（nullity），表示成：$dim(ker(\phi))$。

而在电路例子中，它表示的是所有六个电势差都是0，也就意味着：所有四个电压值是相等的，在零空间中的每个$x$都是一个常向量：$x=(c,c,c,c)$。所以，$A$的零空间是一条线。无论我们怎么同时升高或降低电压量$c$，都不会改变电势差0。

刚才我们说的是电压，现在我们来具体看看关联矩阵在基尔霍夫电流定律上的运用。我们来定义一个拥有4个节点和5条边的图：

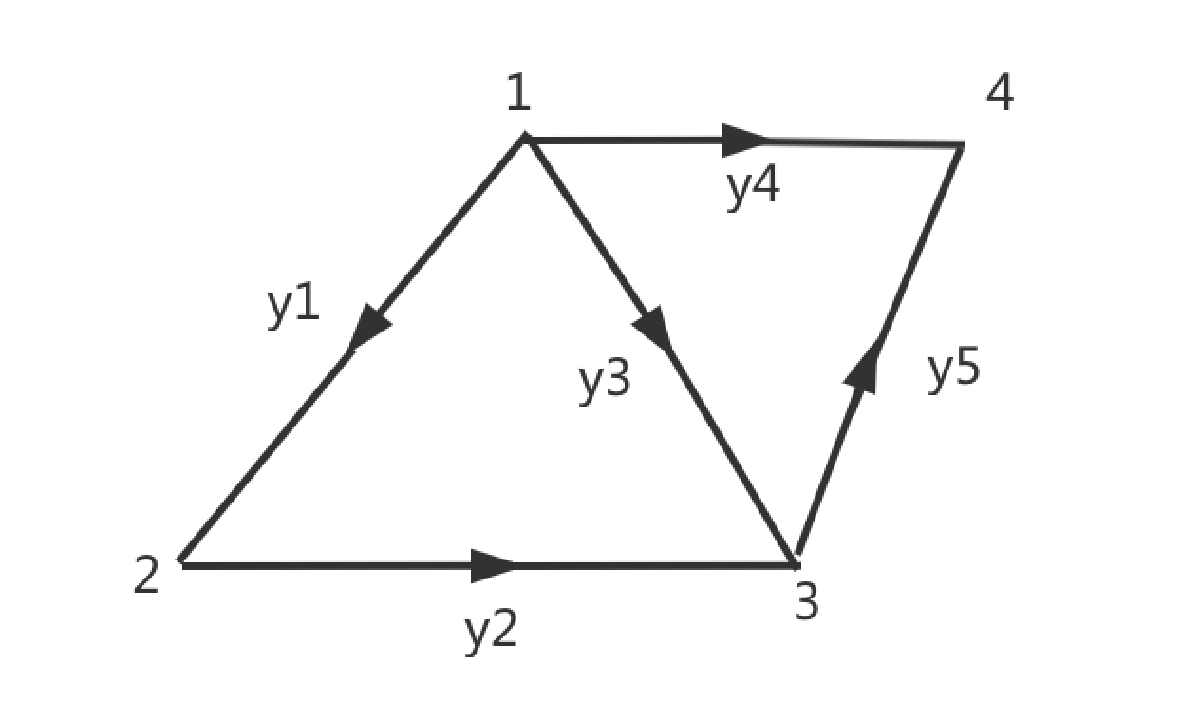
基尔霍夫电流定律定义：$A^{T} y=0$，其中y是向量$y_{1}, y_{2}, y_{3}, y_{4}, y_{5}$，我们把这个图以关联矩阵的形式写出来就是：

$$\left[\begin{array}{ccccc}
-1 & 0 & -1 & -1 & 0 \\\
1 & -1 & 0 & 0 & 0 \\\
0 & 1 & 1 & 0 & -1 \\\
0 & 0 & 0 & 1 & 1
\end{array}\right]\left[\begin{array}{l}
y_{1} \\\
y_{2} \\\
y_{3} \\\
y_{4} \\\
y_{5}
\end{array}\right]=\left[\begin{array}{c}
0 \\\
0 \\\
0 \\\
0
\end{array}\right]$$

这里-1，0，1的含义上面有所描述，第一行和$y$向量相乘后得到：$-y_{1}-y_{3}-y_{4}=0$，说明从节点1出来的总电流等于0，满足守恒定律；第二行和$y$向量相乘后得到：$y_{1}-y_{2}=0$，说明流入节点2的电流和从节点2流出的电流相等；同样，后面两行分别和$y$向量相乘后得到：$y_{2}+y_{3}-y_{5}=0$和$y_{4}+y_{5}=0$，和图表示的都一致，也都符合守恒定律。

好了，到这里简单电路的数学知识，也就是关联矩阵讲完了，如果碰到更复杂的电路，比如：在节点之间，也就是边上有电流源，那么，等式就要从$A^{T} y=0$变成$A^{T} y=f$。

本节小结

本节是第一篇应用篇，所以我从更贴近生活的例子来讲解线性代数的应用，通过弹子锁具，让你能够了解，邻接矩阵与图论之间是怎么关联的；通过基尔霍夫定律，让你能够了解关联矩阵与图论之间是怎么关联的。

所以，邻接矩阵、关联矩阵的最大意义就是用数学的方式描述图，进而来描述某些事物之间的某种特定关系，是不是发现问题后通过数学工具来解决问题很美妙呢？

线性代数练习场

这次的练习题稍微有些难度，是一道传统练习题。

三名商人各带一个随从乘船渡河，现有一只小船只能容纳两个人，由他们自己划行，若在河的任一岸的随从人数多于商人，他们就可能抢劫财物。但如何乘船渡河由商人决定，试给出一个商人安全渡河的方案，使得渡河的次数最少。

注意：这里的问题包含两层含义——安全渡河和渡河次数最少。
提示：使用本节的第一个例子的邻接矩阵和$A^{k}$来解这道题。

欢迎在留言区晒出你的运算过程和结果，我会及时回复。同时，也欢迎你把这篇文章分享给你的朋友，一起讨论、学习。