你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我要讲的内容是“如何从计算机的角度来理解线性代数”。
基础和应用篇整体走了一圈后,最终我们还是要回归到一个话题——从计算机的角度来理解线性代数。或者更确切地说,如何让计算机在保证计算精度和内存可控的情况下,快速处理矩阵运算。在数据科学中,大部分内容都和矩阵运算有关,因为几乎所有的数据类型都能被表达成矩阵,比如:结构化数据、时序数据、在Excel里表达的数据、SQL数据库、图像、信号、语言等等。
线性代数一旦和计算机结合起来,需要考虑的事情就多了。你还记得开篇词中我讲到的四个层次的最后一层——“能够踏入大规模矩阵计算的世界”吗?当我们面对大规模矩阵的时候,计算机的硬件指标就需要考虑在内了,这也是硬性的限制条件。在碰到大规模矩阵的时候,这些限制条件会被放大,所以精度、内存、速度和扩展这四点是需要你思考的。
接下来,我就从这几点深入讲解一下。
首先是精度,我们先从计算机如何存储数字的角度入手,来做一个练习。你可以执行一下这个Python代码,想想会发生什么情况呢?
def f(x):
if x <= 1/2:
return 2 * x
if x > 1/2:
return 2*x - 1
x = 1/10
for i in range(80):
print(x)
x = f(x)
这个结果可能会和你想象的有很大的不同。
其实数学和计算机之间存在很大的不同,数学是连续的、无穷的,而计算机是离散的、有限的。就像这个练习,计算机存储的数字精度是有限的,而很小的误差通过很多次的迭代会累加,最终放大成比较大的错误。一个惨痛的例子就是1996年欧洲航天局的Ariane 5号火箭的发射失败,最后发现问题出在操作数误差上,也就是64位数字适配16位空间发生的整数溢出错误。
那我们该怎么来理解数学是连续的,而计算机是离散的呢?举个简单的例子,我们来看下数学中的区间表达[1,2],这个形式就是连续的;但如果在计算机中以双精度来表达同样的东西,则会是这样的离散形式:
$$
1,1+2^{-52}, 1+2 \times 2^{-52}, 1+3 \times 2^{-52}, \ldots, 2
$$
于是,我们就引出了一个计算机领域精度计算的概念——机械最小值(EPSILON),对于双精度来说,IEEE标准指定机械最小值是:$ε=2^{-53}$。
刚才我们看的是数字精度,现在我们接着来看看矩阵的存储方式。我们都知道,内存是有限的,所以,当你面对大矩阵时,千万不要想着把矩阵所有的元素都存储起来。解决这个问题的一个最好方式就是只存储非零元素,这种方式就叫做稀疏存储。稀疏存储和稀疏矩阵是完美匹配的,因为稀疏矩阵大部分的元素都是零。
我们来看一个机器学习中比较简单的稀疏矩阵的例子:Word Embedding中的One-Hot编码。One-Hot编码就是给句子中的每个字分别用一个0或1编码,一个句子中有多少个字,就有多少维度。这样构造出来的矩阵是很大的,而且是稀疏矩阵。比如:“重学线性代数”这六个字,通过One-Hot编码,就能表达成下面这样的形式。
$$
\left[\begin{array}{llllll}
1 & 0 & 0 & 0 & 0 & 0 \\\
0 & 1 & 0 & 0 & 0 & 0 \\\
0 & 0 & 1 & 0 & 0 & 0 \\\
0 & 0 & 0 & 1 & 0 & 0 \\\
0 & 0 & 0 & 0 & 1 & 0 \\\
0 & 0 & 0 & 0 & 0 & 1
\end{array}\right]
$$
所以,一般稀疏矩阵的大致形态如下图所示。
$$
\left[\begin{array}{llllllll}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\\
0 & 0 & 2 & 0 & \frac{1}{2} & 0 & 0 & 0 \\\
0 & 0 & 0 & 1 & 0 & 0 & 2 & 0 \\\
0 & 0 & \frac{1}{2} & 0 & 4 & 0 & 0 & 0 \\\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\\
0 & 0 & 0 & 1 & 2 & 0 & 1 & 0 \\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1
\end{array}\right]
$$
也有特殊类型的结构化矩阵,比如:对角线矩阵、三对角矩阵、海森堡矩阵等等,它们都有自己的特殊稀疏表达,也都通常被用来减少内存存储和计算量。可以说,数值线性代数在运算方面更多地聚焦在稀疏性上。
接下来我们再来看速度。速度涉及到很多方面,比如计算复杂度、单指令多数据矢量运算、存储类型和网络等。
算法通常由计算复杂度表达,同一问题可用不同算法解决,而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适的算法或者优化算法。
那么我们该如何评价一个算法呢?主要就是从时间复杂度和空间复杂度来综合考虑的。从矩阵计算的角度看,计算复杂度的考虑是很有必要的。简单的计算,我们可以用直接法来计算,而有的比较复杂的计算就要用间接迭代法了。特别是在很多场景中会用到的大型稀疏矩阵,这些计算复杂度都是不同的。我在第4篇“解线性方程组”中提到了迭代法,你可以回顾一下,同时你也可以参考上一节课的迭代法应用细节。
现代CPU和GPU都支持在同一时间以同步方式执行同一条指令。
举个例子来说,一个向量中的4个浮点数的指数幂运算可以同时执行,从而极大地提高运算效率,这类单指令多数据矢量运算处理就叫做SIMD(Single Instruction Multiple Data)。这在矩阵运算中非常重要,虽然我们不用太关心底层的实现,但如果你可以了解一些矩阵运算的包和库,那么你就可以在实际的开发中直接使用它们了,其中比较出名的就是python的NumPy,以及BLAS(Basic Linear Algebra Subprograms)和LAPACK。
LAPACK是用Fortran写的,这里也纪念一下Fortran创始人约翰·巴库斯(John W. Backus),不久前在美国俄勒冈州的家中去世,享年82岁。
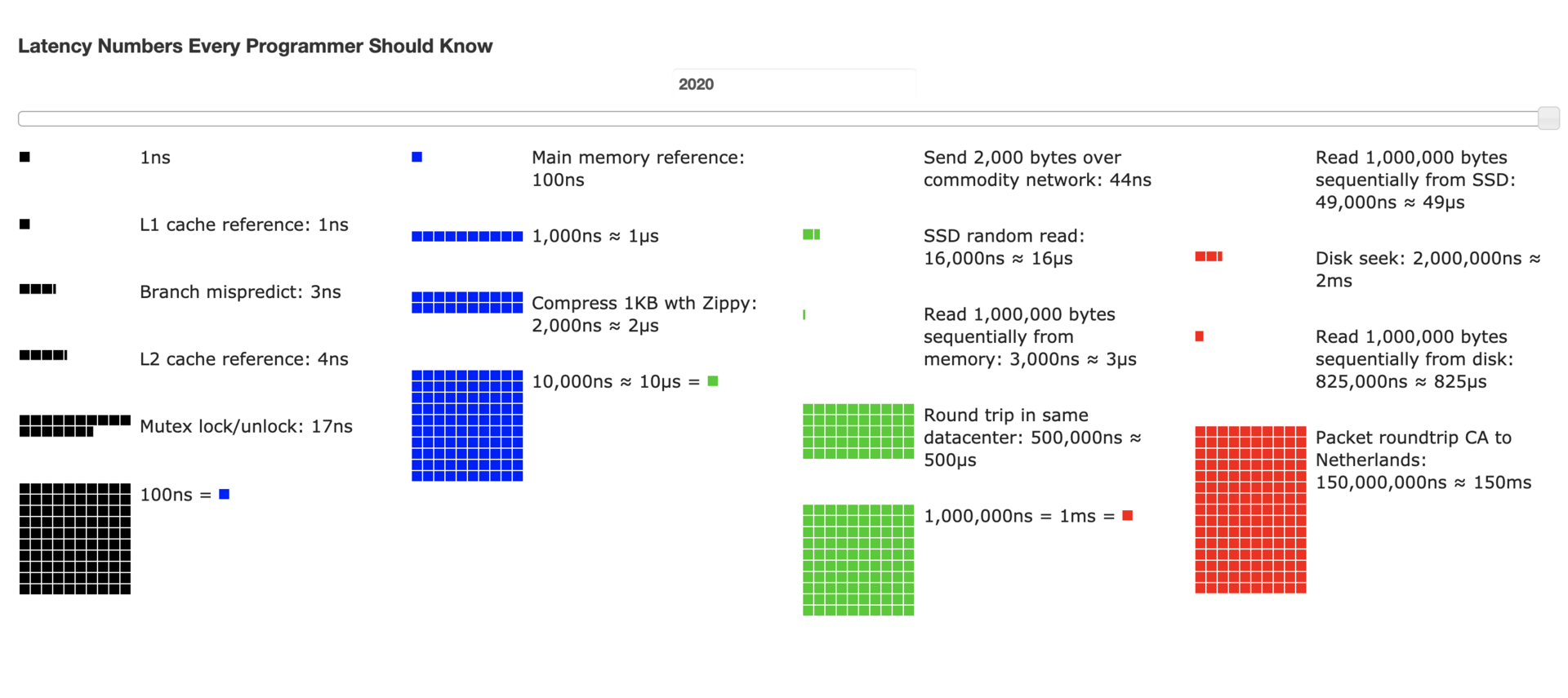
计算机存储类型有很多,比如:缓存、内存、机械盘、SSD,这些不同存储媒介的存储延迟都是不一样的;在网络方面,不同IDC、地区、地域的传输速率也是不同的。

上图中的这些数据是所有程序员必须要知道的,因为毕竟各类计算机资源是有限的,在做解决方案时,必须综合考虑存储和网络的性能和成本来做组合,最终达到最大的产出投入比。这些数据来自GitHub,可以调整年限值来观察每年的动态变换。
最后我再来讲一下扩展,扩展分为单机多核、多处理器的垂直方向扩展,以及多节点平行方向扩展。
当我们想要利用多处理器能力来处理大型矩阵运算的时候,传统的方法就是把大矩阵分解成小矩阵块。比如:一台拥有4个处理器的服务器,现在有这样的两个6×6矩阵$A$和$B$要做乘运算。
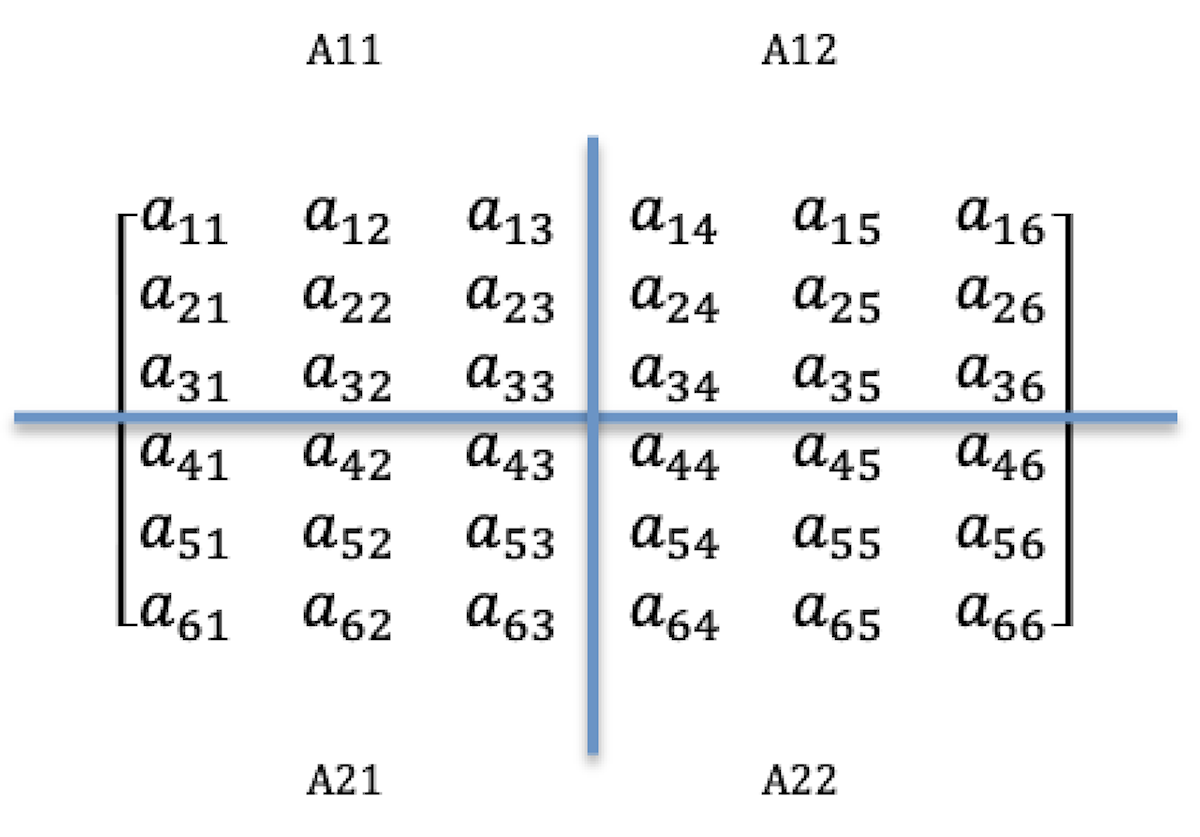
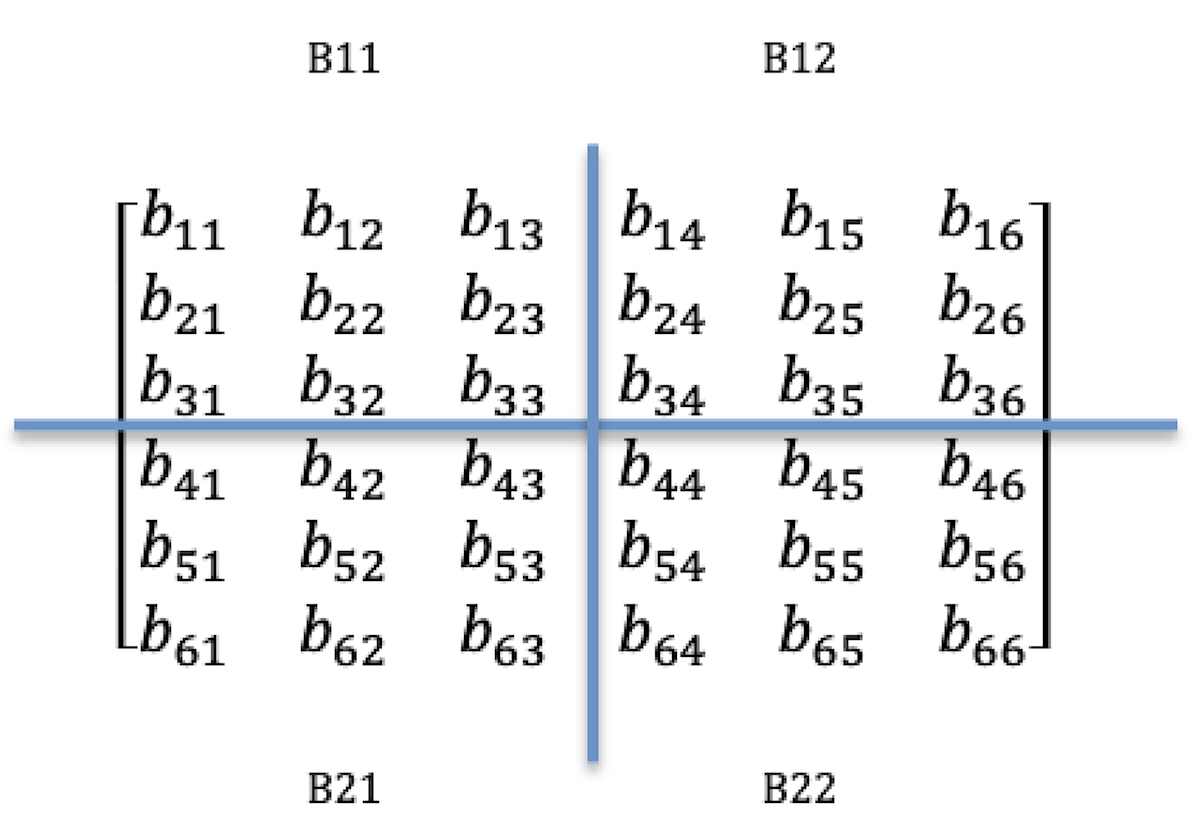
我们可以把这两个矩阵分别分成四块,每块都是3×3矩阵,例如:$A11、A12、A21$和$A22、B11、B12、B21$和$B22$,$A$和$B$的乘运算就是把各自分好的块分配到各处理器上做并行处理,处理后的结果再做合并。
比如:处理器P1处理$A11$和$B11$,处理器P2处理$A12$和$B12$,处理器P3处理$A21$和$B21$,处理器P4处理$A22$和$B22$。于是,4个处理器分别处理$A$和$B$的乘计算来获取结果:$C11、C12、C21$和$C22$。拿$C11$来看,$C11=A11×B11+A12×B21$,虽然$B21$不在P2中,但可以从P3传递过来再计算。
当计算机垂直扩展到极限后,就需要考虑扩展到多节点计算了,其实原理也是一样的,不一样的是需要从应用层面来设计调度器,来调度不同的计算机节点来做计算。
线性代数运用在计算机科学中就是数值线性代数,它是一门特殊的学科,是特别为计算机上进行线性代数计算服务的,可以说它是研究矩阵运算算法的学科。这里,你需要掌握很重要的一个点就是:数学和计算机之间存在很大的不同,数学是连续的、无穷的,而计算机是离散的、有限的。
所以,从计算机角度来执行矩阵运算,需要考虑很多方面:精度、内存、速度和扩展,这样,你在做解决方案时,又或者在写程序时,才能在计算机资源有限的情况下做到方案或程序的最优化,也可以避免类似1996年欧洲航天局的Ariane 5号火箭发射失败的这类错误。
我想让最后一篇的练习成为一个知识点的补充。
针对矩阵高性能并行计算,我前面在“扩展”一模块讲的是一般传统方法,也就是把大矩阵分解成小矩阵块,利用多处理器能力来处理大型矩阵运算。现在,请你研究一下如何用Cannon算法解决这个问题?
Cannon算法是一种存储效率很高的算法,也是对传统算法的改进,目标就是减少分块矩阵乘法的存储量。而且你也可以把它看成是MPI编程的一个例子。
欢迎在留言区分享你的研究成果,大家一起探讨。同时,也欢迎你把这篇文章分享给你的朋友,一起讨论、学习。
评论