你好,我是黄佳。欢迎来到零基础实战机器学习。
经历过了前面几个项目实战,你是不是想告诉我说,佳哥,机器学习的流程也很简单,似乎只要选个模型并重复5个步骤,就可以搞定任何数据集。
看起来是这样,不过也没有这么简单。模型,谁都可以构建,但是,如何让模型的性能更优,才是我们真正的考验。今天,我们就来谈一个与模型优化相关的重要内容,也就是特征工程。
人们常说,数据和特征决定了机器学习的上限,而模型和算法只是无限逼近这个上限而已。请你想一想,在那些给定数据集的机器学习竞赛中,高手们为什么能在数据集相同、模型也类似的前提下,让模型达到一个很高的预测准确率?其实,就是因为他们大都通过漂亮的特征工程,提高了机器学习的上限。
特征工程说起来很简单,就是指优化数据集的特征,使机器学习算法更起作用的过程,但用好特征工程并不容易。对于很多初学者来说,常常感觉特征工程实现起来种类繁多,五花八门,不知道怎么下手。今天这节课我就来带你解决这一难题。
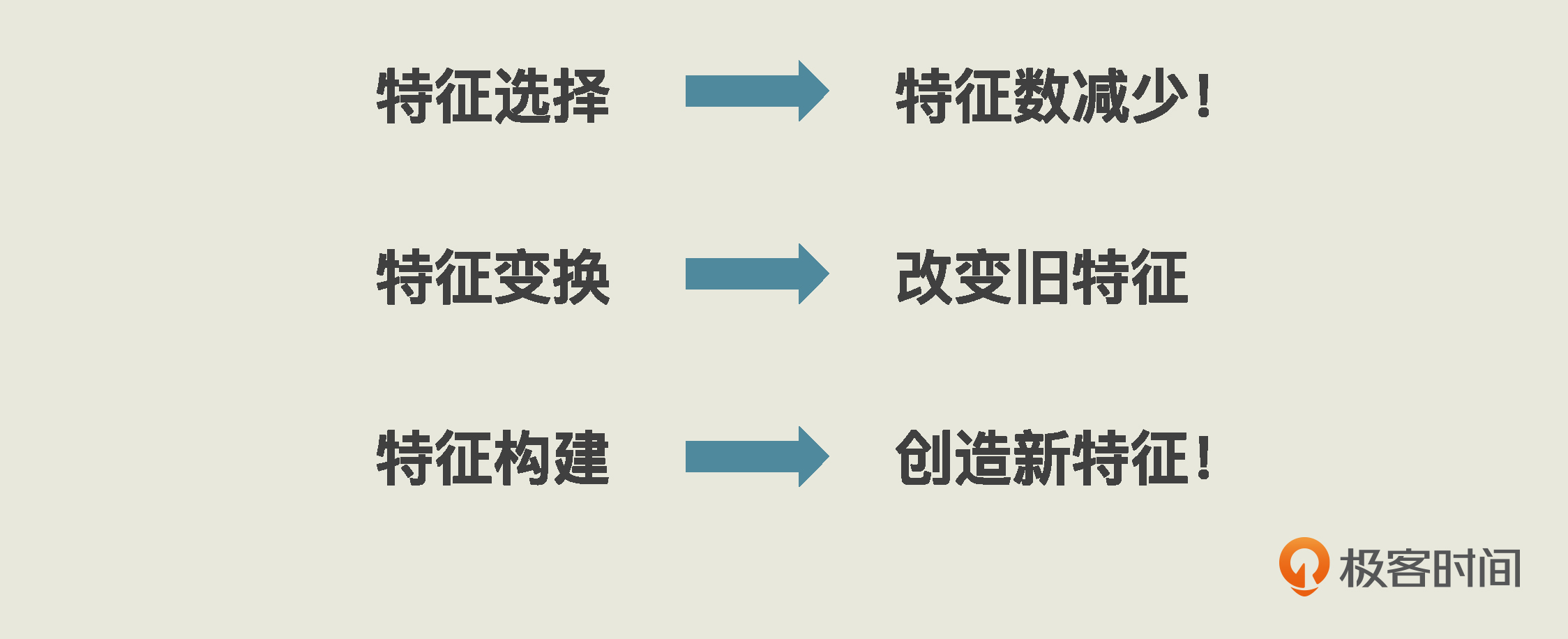
根据我这么多年的经验和理解,特征工程其实是有章可循的。总结起来,几乎所有的特征工程,都逃不开三个基本的思路:特征选择,特征变换和特征构建。只要你掌握了它们,以后每拿到一个新的问题和新的数据集时,都可以从这三个维度去分析。这样,你就不至于无从下手,你的特征工程也不会有大的偏差。
那你肯定很想了解它们都是怎么回事儿,别着急,现在我就跟你一一道来。
其实,在一个数据集中,每个特征在标签预测或分类过程中发挥的作用其实都不同。对于那些没作用和作用小的数据,我们就可以删掉,来降低数据的维度,节省模型拟合时的计算空间。这就是特征选择。
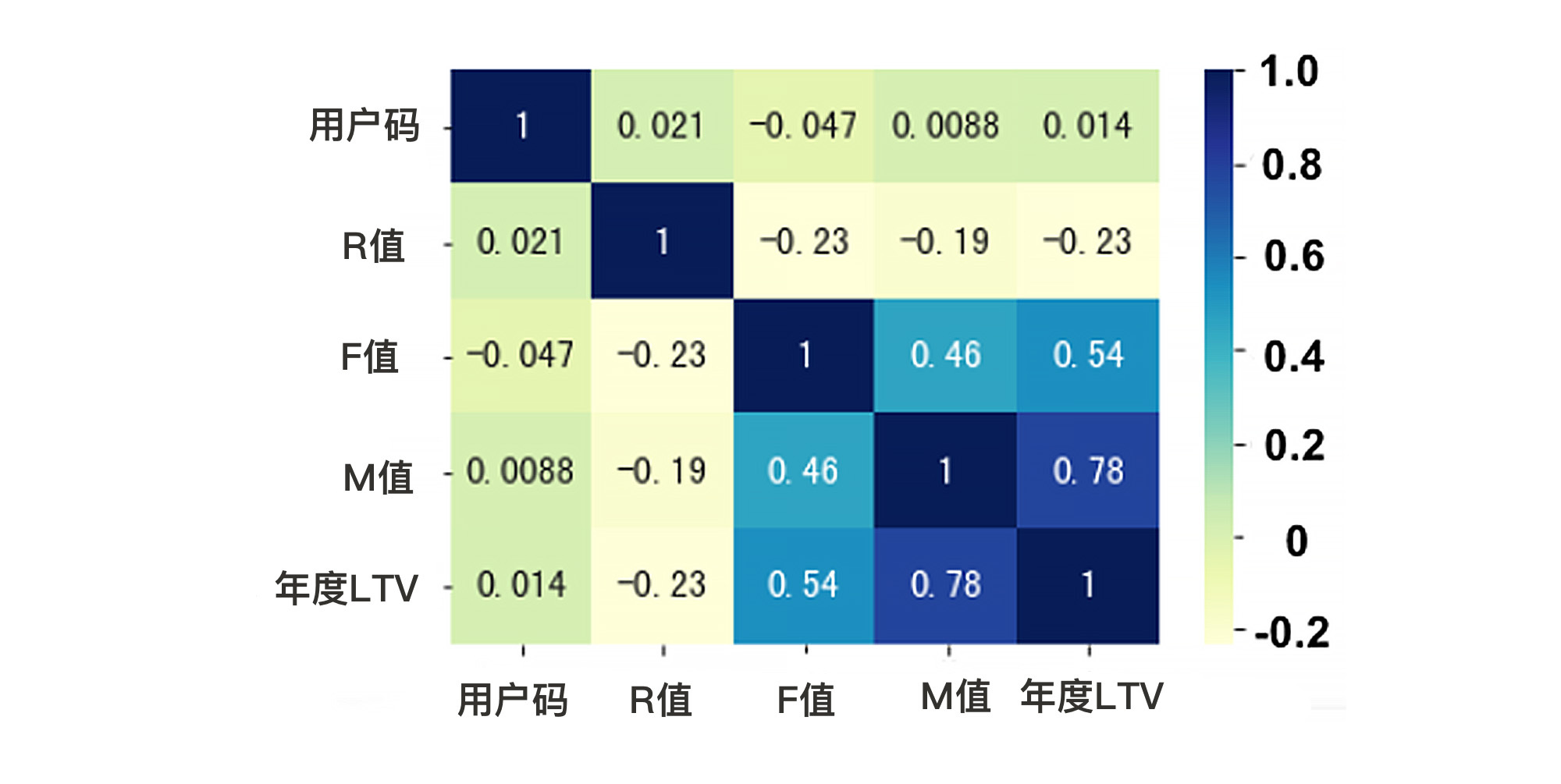
那么,怎么看哪个特征作用大,哪个作用小?我给你介绍一种常用的方法:相关性热力图。就拿我们上节课的项目来说,在我们预测LTV的数据集中,一共有3个特征,分别是“R值”、“F值”和“M值”,还有1个标签“LTV”。这时候,我们就可以通过相关性热力图来看看,哪些特征和标签的相关性更高。
具体的实现过程,就是用corr()方法求出数据集中所有字段之间的相关性,然后用seaborn的heatmap方法,将它以热力图的形式呈现出来:
# 对所有的标签和特征两两显示其相关性热力图(heatmap)
import seaborn as sns
sns.heatmap(df_LTV.corr(), cmap="YlGnBu", annot = True)
输出如下:

那么怎么去看这个相关性热力图呢?
首先,我们只要聚焦于LTV标签和R、F、M三个特征之间的关系就可以了,用户码这个字段和LTV肯定是不相关的。
然后我们再来看这张图中方格里的数字,这类数字叫做皮尔逊相关系数,表示两个变量间的线性相关性,数值越接近1,就代表相关性越大。那么,自己和自己的相关性当然就是1了。
接下来,你需要知道的是,相关性是有正负的。正值说明是正相关,负值说明是负相关,从图中我们看到,R值和年度LTV的相关性为-0.23,就表明这个数据集中新进度(R)数字越大,年度LTV就越小。你可以想一想这是为什么。
此外,我们还会发现,M值、F值和LTV的相关度比较高,而R值和LTV的相关度比较低。这时候,我们就可以选择丢弃“R值”这个字段。这就是一个特征选择。
X_train_less_feature = X_train.drop(['R值'], axis=1) #特征训练集
X_valid_less_feature = X_valid.drop(['R值'], axis=1) #特征验证集
model_lr_less_feature = LinearRegression() #创建线性回归模型
model_lr_less_feature.fit(X_train_less_feature, y_train) #拟合线性回归模型
print('测试集上的R平方分数-线性回归: %0.4f' % r2_score(y_valid, model_lr.predict(X_valid)))
print('测试集上的R平方分数-少R值特征的线性回归: %0.4f' % r2_score(y_valid, model_lr_less_feature.predict(X_valid_less_feature)))
输出结果如下:
测试集上的R平方分数-线性回归: 0.4410
测试集上的R平方分数-少R值特征的线性回归: 0.4356
在这段代码中,我们用同样的线性回归模型进行拟合、评估,唯一的区别就是特征减少了一个R值。你会发现,在这种情况下训练出来的模型,得分会低一点点,不过变化并不太显著,这就说明“R值”这个特征对函数最终的性能影响确实不大。但是,如果你丢掉的是F值或M值,那么模型的分数将显著降低。
尽管如此,我还是要说明一下,在这个项目的模型训练中,我并不建议你进行这样的特征选择。因为原始的特征数目已经很少了,要是再把R值这样的特征丢弃,显然不合逻辑。我刚才做这样的尝试,只是想为你展示特征选择的思路。
在上面的过程中,我们通过“相关性热力图”,观察了每个特征和标签之间的关系,并手工选择了特征。那么你可能会问,难道没有工具可以帮我们自动进行特征选择吗?当然有。
在sklearn的feature_selection模块中,有很多自动特征选择工具。这里我给你介绍一个常用的单变量特征选择工具,SelectKBest。SelectKBest的原理和使用都非常简单,它是对每个特征和标签之间进行统计检验,根据X 和 y 之间的相关性统计结果,来选择最好的K个特征,并返回。
对于我们的LTV预测数据集来说,我们可以这样调用SelectKBest来选择特征。
from sklearn.feature_selection import SelectKBest, mutual_info_regression #导入特征选择工具
selector = SelectKBest(mutual_info_regression, k = 2) #选择最重要的两个特征
selector.fit(X, y) #用特征选择模型拟合数据集
X.columns[selector.get_support()] #输出选中的两个特征
输出如下:
Index(['F值', 'M值'], dtype='object')
在调用SelectKBest的过程中,我们是指定了参数score_func = mutual_info_regression,其中,mutual_info_regression是用于对连续型标签进行特征评分。如果标签是离散型的,那么就是分类问题,我们就要用过mutual_info_classif来评分了。
从输出的结果来看,F值和M值的分数比R值高。所以,在K=2的情况下,我们就需要在这3个特征中舍弃一个,这时候R值就要被舍弃。这个结果和我们前面观察到的一致。
总体来说,单变量特征选择比较直接,速度快,并且独立于模型。但是,你有没有想过这种做法可能会有一个问题?那就是,如果一个特征表面上和标签不大相关,但是在与另一个特征组合之后,才会具有信息量,那么上面的做法可能会让你错误地舍弃这个特征。
那么,有没有一种考虑了各个特征之间的组合后,才做出特征选择的工具呢?有。不过,这样的多变量组合型特征选择工具必须结合具体的模型存在,也就是说,当所有特征都被输入模型进行拟合时,在这个过程中才能评估出最不重要的特征,然后再进行特征选择。
在sklearn的feature_selection里,有下列几种在拟合特定模型时进行特征选择的工具,你可以选择使用:

除了这些特征选择工具,我认为“数据降维”也可以归入到特征选择中。当然,也有人把降维视为一种独立的特征工程类型。
那什么是数据降维呢? 其实就是通过特定算法,把多维特征压缩成低维的特征,也就是通过算法实现特征选择,减少特征的数目。常见的降维算法有两种:主成分分析法(PCA)和线性判别分析(LDA)。PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。出于咱们的课程定位,这些降维算法我们并不会过多涉及。
另外,还有一种方式,就是用深度学习来进行特征选择,这在计算机视觉领域十分普遍。因为深度学习具有自动学习特征的能力。就拿图片识别来说,当图片被输入到卷积神经网络后,网络会自动形成一条条特征通道,选择提取有用的信息来进行最终的目标模型训练。
不过,神经网络中的这些特征通道是怎么形成的,我们目前还没有很好的方式用数学手段去推导、确定,它对于我们来说就像一个黑箱。
总而言之,特征选择的目标是,尽量保持对模型训练有效的信息,与此同时减少数据集的特征数量。
除了特征选择外,还有一种特征工程是在原有特征的基础上进行加工,没有减少特征数,这就是特征变换。
特征变换的整体目标是让原始特征变得机器学习模型可用,甚至是更好用。
要搞清楚特征变换,我们就得先了解一下特征的类型。其实,特征和标签一样,也分为连续和离散两类。像分数、点击量这些,就属于连续特征(continuous feature);而离散特征(discrete feature),也叫类别特征(categorical feature),像男生、女生,或者说北京、上海、深圳、广州等等,这些都属于离散特征。
不同的特征类型,有不同的特征变换方式。对连续特征来说,我们最常见的特征变换就是特征缩放(feature scaling),也就是改变特征的分布或者压缩特征的区间。因为有很多模型都喜欢范围比较小、分布有规律的数据,比如采用梯度下降方法求解最优化的模型,较小的数值分布区间能够提升收敛速度,还有SVM、KNN、神经网络等模型,都要求对特征进行缩放。
在sklearn中,特征缩放方法很多:

下面是各个特征缩放方法从原始特征到新特征的缩放效果图,你可以看看:
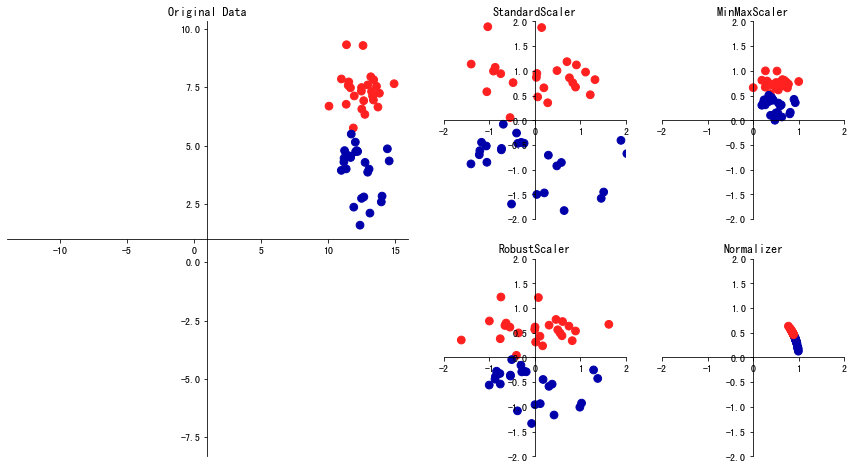
下面,我们选择其中最常见的两个特征缩放工具StandardScaler和MinMaxScaler,来预测用户LTV,比较一下它们的优劣。你要注意,这里所谓的优劣,仅针对于这个特定数据集和特定问题而言。
由于大部分的代码和实战中介绍过的相同,我这里就不再重复了。下面我只是展示和特征工程相关的代码,你可以在这里下载到完整的代码。
首先,我们调用StandardScaler,进行数值特征的标准化缩放,这个缩放将形成正态分布的新特征。
from sklearn.preprocessing import StandardScaler #导入标准化缩放器
scaler = StandardScaler() #创建标准化缩放器
X_train_standard = scaler.fit_transform(X_train) #拟合并转换训练集数据
X_valid_standard = scaler.transform(X_valid) #转换验证集数据
X_test_standard = scaler.transform(X_test) #转换测试集数据
在上面的代码中,你要特别注意,在创建标准化缩放器之后,我们对于训练集使用了fit_transform这个API,这是fit和transform两个API的整合,它的意思是先根据训练集拟合数据,找到合适的标准化参数,然后再把参数应用在训练集上,给数据做缩放。
而在验证集和测试集上,我们只使用transform这个API,来通过从训练集中得到的参数,来转换数据,这个步骤中就没有fit的过程,这是因为对于模型来说,验证集和测试集是新的看不见的数据,因此在训练之前或训练期间它是不应该被访问的,使用来自验证集和测试集的任何信息都属于数据泄露,会导致评估性能的潜在偏差。
这也就是为什么特征缩放必须在拆分完训练集和测试集后进行,因为它的参数只能来自训练集的数据。
然后,我们用缩放后的特征训练模型,得到一个随机森林模型model_rfr_standard。这里的rfr是一个缩写,代表random forest refressor,也就是随机森林回归。
model_rfr_standard = RandomForestRegressor() #创建随机森林回归模型
model_rfr_standard.fit(X_train_standard, y_train) #拟合随机森林模型
讲完了StandardScaler,我们再用MinMaxScaler来预测用户LTV。进行数值特征的归一化缩放。所谓“归一化”,就是把特征的值压缩到给定的最小值和最大值,比如0-1之间。如果有负值的话,那就是-1到1之间。
与标准化的过程相同,在对验证集和测试集进行归一化时,我们也应该按原样,使用先前从训练集中获得的归一化参数,而不是在验证集和测试集上重新计算它们。
from sklearn.preprocessing import MinMaxScaler #导入归一化缩放器
scaler = MinMaxScaler() #创建归一化缩放器
X_train_minmax = scaler.fit_transform(X_train) #拟合并转换训练集数据
X_valid_minmax = scaler.transform(X_valid) #转换验证集数据
X_test_minmax = scaler.transform(X_test) #转换测试集数据
然后,我们用缩放之后的特征训练模型,得到一个随机森林模型model_rfr_minmax。
model_rfr_minmax = RandomForestRegressor() #创建随机森林回归模型
model_rfr_minmax.fit(X_train_minmax, y_train) #拟合随机森林模型
那到这里,我们就得到了两个随机森林模型:model_rfr_standard和model_rfr_minmax。我们拿这两个模型,和不使用特征缩放训练出来的模型,整体做一个对比,看看这三种模型在验证集上的分数怎么样。这里我把评估的结果用柱状图来展示了(对应的代码你可以参见这个链接):
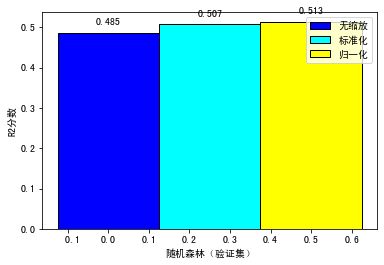
可以看到,对于预测用户LTV这个项目来说,采用特征缩放,尤其是MinMaxScaler,模型在验证集上会得到较优的结果。
你也许会问,数值型特征常见的变换是特征缩放,那么类别型特征呢?其实对于类别型特征来讲,最常见的变换方式是通过虚拟变量(也叫哑编码或者哑变量)把机器不能读取的类别文本,转换成一个个的0、1值。
把类别特征转换成机器可以读取的编码,也非常简单。如果数据表中的字段值是“男”、“女”这样的数据,我们就用下面的代码直接转换成0、1值即可。
df['性别'].replace(to_replace='女', value=0, inplace=True)
df['性别'].replace(to_replace='男', value=1, inplace=True)
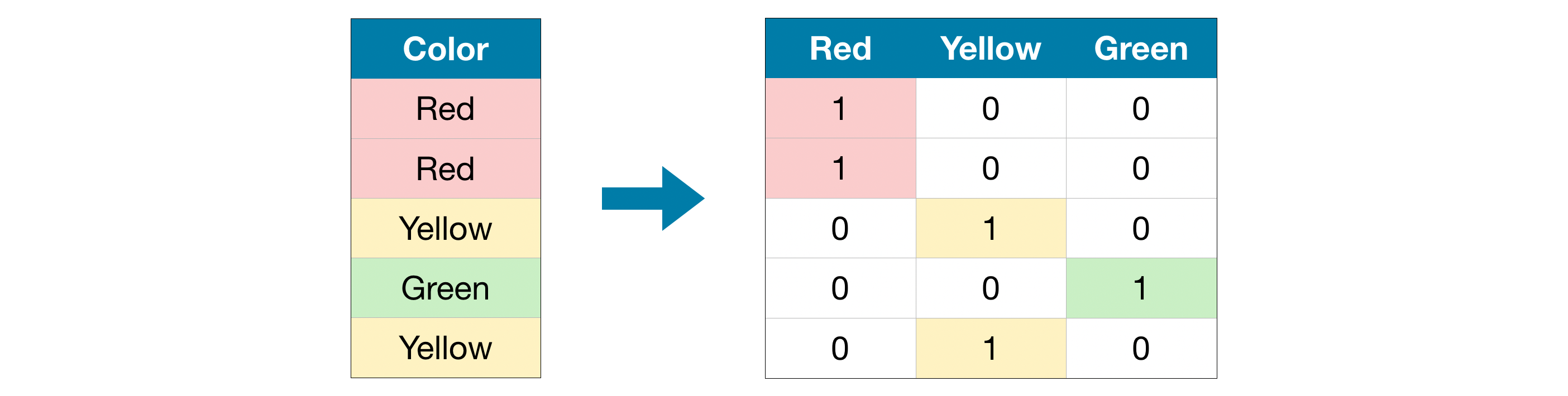
对于两个以上的分类,pandas编码有一种非常简单的方法,就是get_dummies函数。get_dummies函数会自动变换所有具有对象类型(比如字符串)的列或所有分类的列,而分类特征的每个可能取值都会被扩展为一个新特征,并且每一个新特征只有0、1两种取值。这个过程就是虚拟变量的生成过程,你看看这张图就会比较清楚了。
下面我们就把上一个项目中的订单数据集里的“城市”转化为虚拟变量。对于这一步,其实我在之前的课程中给你留过作业,并给出了“提示”,这里我就用和提示不大一样的代码,来实现相同的功能。
# 把多分类字段转换为二分类虚拟变量
category_features = ['城市'] #要转换的特征列表
df_sales = pd.get_dummies(df_sales, drop_first=True, columns=category_features) #创建哑变量
df_sales #显示数据
输出如下:
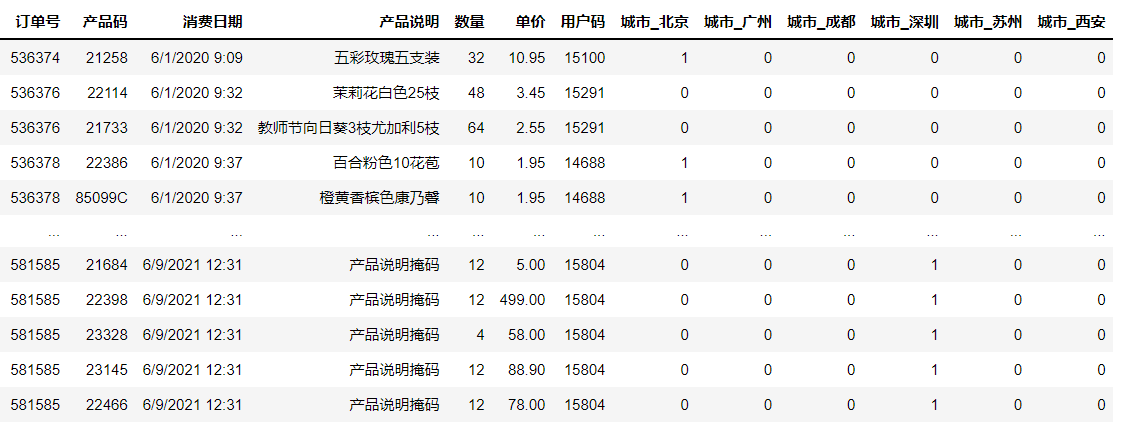
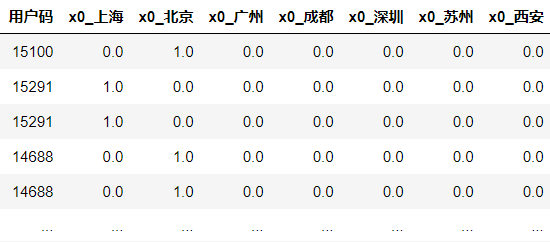
可以看到,原来的城市字段,变成了多个二分类字段,比如城市_北京、城市_成都等,并且每个字段只有0、1值,这样的编码格式就可以被机器识别。
这里呢,我要请你特别注意一下drop_first这个参数。这个参数实际上控制着get_dummies函数返回的结果,值为True返回结果是虚拟变量(Dummy Variable),值为False则返回独热编码( One Hot Encoding)。
独热编码与虚拟变量非常相似,它们的不同之处在于:在虚拟编码方案中,当特征具有 m 个不同类别标签时,我们将得到 m-1 个二进制特征,作为基准的特征被完全忽略;而在独热编码方案中,我们将得到 m 个二进制特征。因此,你仔细观察上面get_dummies的结果,就会发现“城市_上海”这个特征没有被生成。而如果你把drop_first设为False,“城市_上海”就会出现。
那么,为什么要有这样的区别呢?主要有两个原因。第一个原因是,如果有N个特征,并且前N-1个特征的值是已知的,那么第N个特征的值也就知道了。因此,独热编码有冗余,虚拟变量没有冗余。举个例子,对于用户来说,如果其它所有城市的值都是0,唯独“上海”这个字段的值不知道,我们自然就能推知这个用户是属于上海这个城市,因为这是仅有的可能性了。
第二个原因是,独热编码的这种冗余会导致共线性问题,也就是自变量之间存在高度相关关系,不总是相互独立的,从而使模型参数估计不准确。不过,这也意味着,独热编码可以直接从“1”值看出所对应的类别,而虚拟变量需要进行推理。因此独热编码比较直观,虚拟变量没有那么直观。
那我们应该在什么时候使用虚拟变量,在什么时候使用独热编码呢?如果线性模型有截距项,就使用虚拟变量;如果线性模型无截距项,那么使用独热编码。
此外,在线性模型有截距项的情况下,如果使用正则化,那么也推荐使用独热编码,因为正则化能处理多余的自由度,可以约束参数;如果不使用正则化,那么就使用虚拟变量,这样多余的自由度都被统摄到截距项intercept里去了。关于正则化的进一步说明,我会在下一讲详细介绍。
上面所说的虚拟变量和独热编码是对类别型特征的处理,不过在某些情况下,我们还需要把数值型特征离散化。
你可能会奇怪为什么要对特征做离散化处理?这是因为,当特征的数量级跨度过大,而且与标签的关系又非线性的时候,模型可能只对大数量级的特征值敏感,也就是说模型可能会向大特征值的那一侧倾斜。另外,模型的运算速度也会受到影响。
比如说,一个特征的数据值为[3.5, 2.7, 16.9, 5.5, 98],这里的“98”明显偏离其他数据,很容易影响到模型的效果。这时候我们就可以把这些数值做个离散化,比如把小于5的值记为“0”,大于5且小于10的值记为“1”,大于10的值记为“2”,那么[3.5, 2.7, 16.9, 5.5, 98]就可以变成0、1、2这样的离散值,也就是[0,0,2,1,2],这不仅能减弱像“98”这样的异常数据的权重,还能提高模型的运算速度。
我们在这里用的方式呢,就叫做分桶,分桶也叫分箱,就是指将连续型特征离散化为一系列的离散值。而这里的0、1、2呢,就是我们说的“桶”或者“箱”了。
对数值进行分桶,我们首先要确定两点:一是桶的数量,二是把什么范围的数据分成一个桶,也就是桶的宽度是多少。在这个过程中,常规的做法有三种:
等距分桶:每个桶的宽度固定,如 0-99,100-199,200-299等。这种方式适合样本分布比较均匀的情况,如果样本分布不均,就容易出现有的桶多、有的桶少的情况。
等频分桶:每个桶有一样多的样本,但可能出现数值相差很大的样本放在同一个桶的情况。
模型分桶:利用模型找到最佳分桶。比如决策树模型,它本身就具有对连续型特征切分的能力,因此我们可以利用分割点进行特征离散化。再比如聚类模型,可以将连续性特征分成多个类别。在之前的用户画像项目中,我们对R值、F值、M值进行聚类,就是一种模型分桶操作,即把连续的数值切分成这三维度的离散类别。
到这里,我们就了解了两种特征工的基本思路,一种是通过特征选择减少特征的维度,另一种是通过特征变换加工原始特征。你可能会问我,有没有什么方法能根据原始数据创造出新的特征呢?
自然是有的,这就是第三种特征工程类型:特征构建。
特征构建是整个特征工程领域最具创造力的部分,也是我觉得在数据预处理环节中最有意思的地方。因为它完全没有一定之规,全凭借你的经验、领域知识和创造力。就像我们在获客关的项目实战里,从原始的订单数据集中,我们经过整理和组合原始数据,求出了三个完全不存在于原始数据集中的新值:R值、F值和M值,这就是一个典型的特征构建。
为什么我们知道要构建这三个值?就是因为我们具有运营领域的经验和相关知识,知道R值、F值和M值对用户分组画像是重要的因子,能够输入到聚类模型和回归模型中去。
所以,要想把原始数据集中的特征工程做好,就要不断积累经验和知识,展开自己的想象力,看看可以构建出什么样有用的新特征,能让机器学习模型学得更好。
这里我再给你举一个例子。假设我们现在有一个航班的旅客订单信息数据集,记录了几年内每一天航班的旅客订票情况。通过这个数据集,我们要帮航空公司构建一个模型,来预测未来某天的客流量。那么,你能想到什么特征工程方法,有可能提高模型的效率?
其实,我们可以根据“订单日期”这个字段,再人工添加一个新字段,来标明每一天的具体航班是在国家公休假日的之前、之中还是之后,或并不靠近公休假日。这个方法,其实是把与预测客流量这个任务的相关先验知识编码到了特征中,以辅助机器学习算法理解为什么流量会出现可能的波动。
当然,添加一个新特征并不意味着机器学习算法肯定会用到它,即使模型发现假日信息和客流量没啥关联,那也无伤大雅。但是,如果真的有关联,这个新特征就会提高模型的预测准确率,尤其是当预测未来公休假日附近的客流量时,会更准。
为了让你进一步理解特征构建的作用,我再用一个例子,通过程序代码和示意图来直观地给你进行展示。这次,我们读入一个简单的数据集“特征构建示意数据集”(你可以在这里下载数据集),来看看特征X和标签Y之间的关系,然后思索一下怎么拟合二者。
import pandas as pd #导入Pandas
import numpy as np #导入NumPy
import matplotlib.pyplot as plt #导入绘图工具
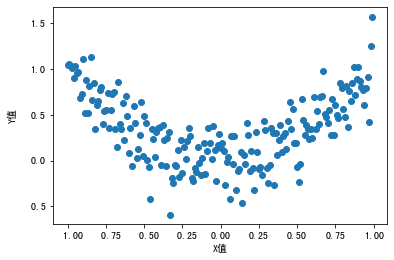
df = pd.read_csv('特征构建示意数据集.csv') #导入数据
plt.scatter(df.X, df.Y) #X,Y散点图
输出显示,这个数据集中的特征X和标签y呈现一种符合回归模型的趋向。
如果我们用线性回归进行建模,就会得到一个线性回归模型:
from sklearn.model_selection import train_test_split #导入train_test_split
df_x = df['X'].to_frame() #特征集
df_y = df['Y'] #标签集
X_train, X_test, y_train, y_test = train_test_split(df_x,df_y,test_size=0.3, random_state = 0) #拆分数据集
from sklearn.linear_model import LinearRegression #导入LinearRegression
model = LinearRegression() #创建模型
model.fit(X_train, y_train) #拟合模型
plt.scatter(df.X, df.Y) #散点图
plt.plot(X_test, model.predict(X_test),linestyle='--', color = 'red') #显示拟合曲线
输出这个模型,可以看到这个回归线并不能很好地拟合从X到Y的关系:
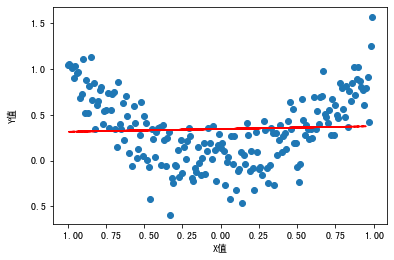
那怎么办呢?其实,我们从图中可以观察到,X-Y之间的关系其实更接近多项式回归(polynomial regression)中的二项式回归,也就是说,Y是X的二次函数。那么,我们就在X的基础上做个平方,构建出一个新特征。
X2_train = X_train.copy() #新特征训练集
X2_test = X_test.copy() #新特征测试集
X2_train['X2'] = X2_train['X']**2 #构建新特征X2
X2_test['X2'] = X2_test['X']**2 #构建新特征X2
model2 = LinearRegression() #创建新模型
model2.fit(X2_train, y_train) #拟合新模型
plt.scatter(df.X, df.Y) #散点图
plt.scatter(X_test, model2.predict(X2_test), linestyle='--', color = 'red') #新拟合函数曲线
这里,我们还是用一样的模型来拟合,并显示原始特征X和预测值之间的关系。这时候我们发现,拟合曲线更趋近于X和Y的真实关系:
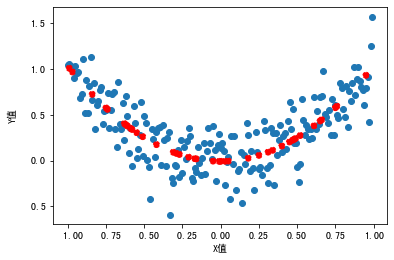
是不是很奇妙呢?希望通过这个小例子,你能理解:在实践中,我们所使用的特征,以及特征与方法之间的匹配,通常都是让机器学习模型能够有良好表现的最重要因素。
好了,这节课到这里就结束了,我给你总结了三类重要的特征工程。其中,特征选择可以减少特征的维度,特征变换则能把原始特征塑造的更容易被机器学习模型使用,特征构建则需要你激发极大的创造力,以原始数据为基础去发现对建模有用的新特征。
在这一讲中,我特别为你示范了不少精巧的特征工程小示例,所有的代码你都可以在这里找到。不过师傅领进门,修行在个人,更多特征工程的知识和应用,还有待于你在实践中去继续挖掘。
那么,这一讲我给你留三道思考题:
1.我在前面使用了StandardScaler工具和MinMaxScaler工具做特征缩放,请你用一下别的特征缩放器,看看适不适合我们这个数据集。
2.Sklearn的OneHotEncoder工具和Pandas的get_dummies类似,也可以把整个数据集的字段或者指定的特征字段转换为虚拟变量。请你试一试这个工具。
提示:这个题目较难,涉及数组形状变换。如果遇到麻烦,可以试着上网搜索一下解决方案。
from sklearn.preprocessing import OneHotEncoder #导入OneHotEncoder工具
encoder = OneHotEncoder(sparse=False)
...
df_city = pd.DataFrame(df_city, columns=encoder.get_feature_names())
...
OneHotEncoder输出的结果:
3.你在工作中用特征工程构建过新特征吗?有没有比较巧妙的特征工程可以给大家分享呢?如果你还没有做过特征工程,那么请你谈一谈学了这节课之后,你对特征工程有怎样的理解。
欢迎你在留言区分享你的想法和收获,我在留言区等你。如果这节课帮到了你,也欢迎你把这节课分享给自己的朋友。我们下一讲再见!
