你好,我是黄佳。欢迎来到零基础实战机器学习。
在上一讲中,我们用lifelines包中的工具,在“易速鲜花”的会员信息中,挖掘出了与用户流失相关比性较大的几个因素。今天,运营部门又来了新需求,我们通过这个需求,一起来看看怎么解决二元分类问题。
之前,我们接触的绝大多数业务场景都是回归场景,但是,后面更多的场景实战中,也需要分类算法大显身手,而今天这一讲将为我们解决后续诸多分类问题打下基础,它的重要性不言而喻。
好,让我们直接开始吧!
这回运营部门又提出了什么需求呢?运营部门的同事是这样向你诉苦的:“要留住会员,真的是难上加难。老板要求我们啊,对于每一个流失的客户,都要打电话,给优惠来挽留,还要发一个调查问卷,收集为什么他不再续费的原因,你说这不是事后诸葛亮吗?人都走了,挽留还有什么意思呢?你们数据这块能不能给建立一个模型,预测一下哪些客户流失风险比较高,然后我们可以及时触发留客机制,你看行吗?”
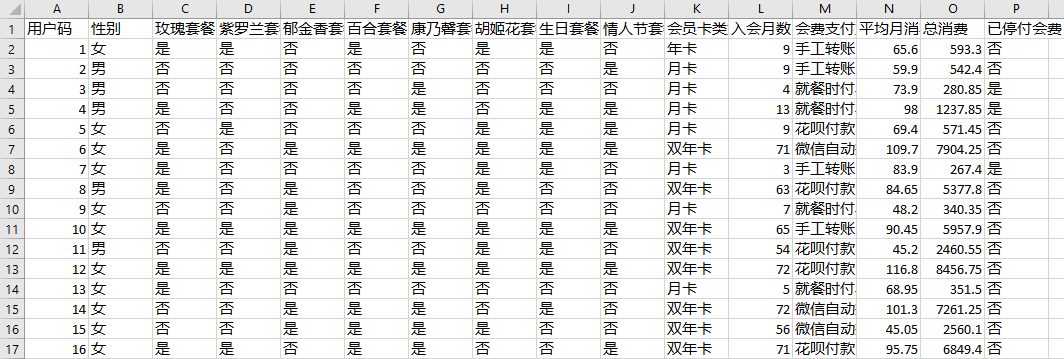
以你现在对机器学习的理解,你觉得这个需求可以做到吗?当然可以。现在,让我们先来回顾一下运营部门给我们的这个数据集。

根据运营同事的描述,我们要预测的标签就是“已停付会费”这个字段。从已有的数据中训练出模型,我们自然就可以推知其它具有类似特征的会员,“停付会费”的可能性大小。
既然有标签,这肯定是一个监督学习问题。再进一步,那它是回归问题,还是分类问题呢?这就要看标签是连续值还是离散值了。“是否已停付会费”这个字段的值,要么为“是”,要么为“否”,也就是非1即0,自然是离散的。所以,这是一个分类问题,而且它还是一个典型的二元分类问题。
因此,机器学习中的分类模型可以告诉我们每一个用户具体的流失风险。如果风险高,那这个用户很有可能会流失,他就需要被运营团队关注了。请你注意,这个“高风险值”是多个特征相组合显现出的结果,并不是单纯取决于某个特征。
分析到这里,我们就开始着手处理了。
对于这个问题来说,数据的读入、清洗、可视化和特征工程等工作,我们在上一讲中已经做好了:
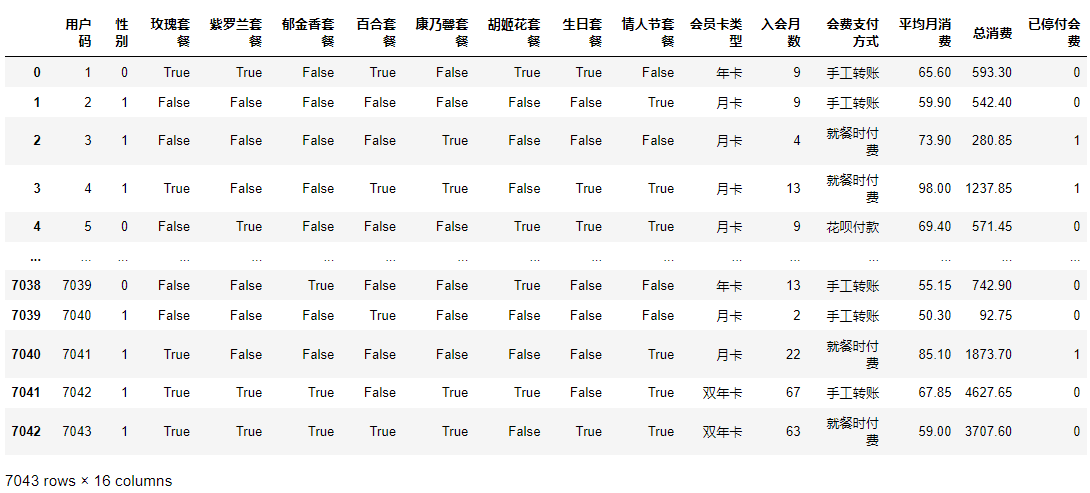
所以,我们就直接来构建特征集和标签集就可以了:
X = df_churn.drop(['Churn'], axis = 1) # 基于df_churn构建特征集
y = df_churn.Churn.values # 基于df_churn构建标签集
然后,我们再来拆分一下训练集和测试集。
from sklearn.model_selection import train_test_split #导入train_test_split模块
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2) #拆分数据集
准备好训练集和测试集之后,我们直接进入算法选择的环节。
我们刚才说,“预测哪些客户流失风险比较高”是一个二元分类问题。那么,能够解决这种分类问题的算法又有哪些呢?在第7讲中,我们在做回归分析时,介绍了很多回归算法。其实,和回归类似,机器学习中能够用来解决分类问题的算法也非常多,我把比较常用的分类算法整理在下面这个表中:

我们说过,在解决具体问题的时候,我们通常会选择多种算法进行建模,相互比较之后,再确定比较适合的模型。不过,在这一讲中,我们不太可能把上面所有的模型都挨个讲解和尝试一遍,所以,我就挑两个没讲过的算法:逻辑回归和神经网络,来带你解决这个问题。如果你对其他模型的效果很感兴趣,可以自行做个尝试。
我们先来看逻辑回归算法。
逻辑回归是最为基础的分类算法,它在分类算法中的地位和和线性回归在回归算法中的地位一样,也常常作为基准算法,其它算法的结果可以与逻辑回归算法进行比较。
其实,逻辑回归的本质仍然是线性回归,这也是为什么它的名字中仍然保留了“回归”二字。只不过,在线性回归算法的基础之上,它又增加了一个Sigmoid函数。
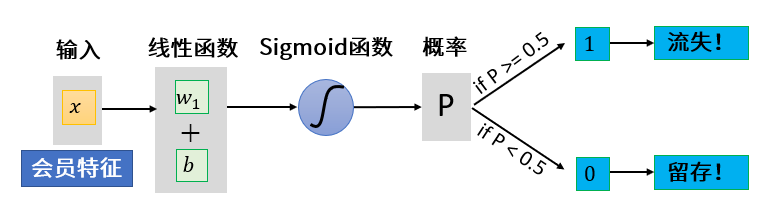
这个函数的作用是什么呢?它其实是在线性回归算法的预测值基础上,把预测值做一个非线性的转换,也就是转换成0~1区间的一个值。而这个值,就是逻辑回归算法预测出的分类概率。这个过程你可以参考下面的Sigmoid函数图像以及它的公式。
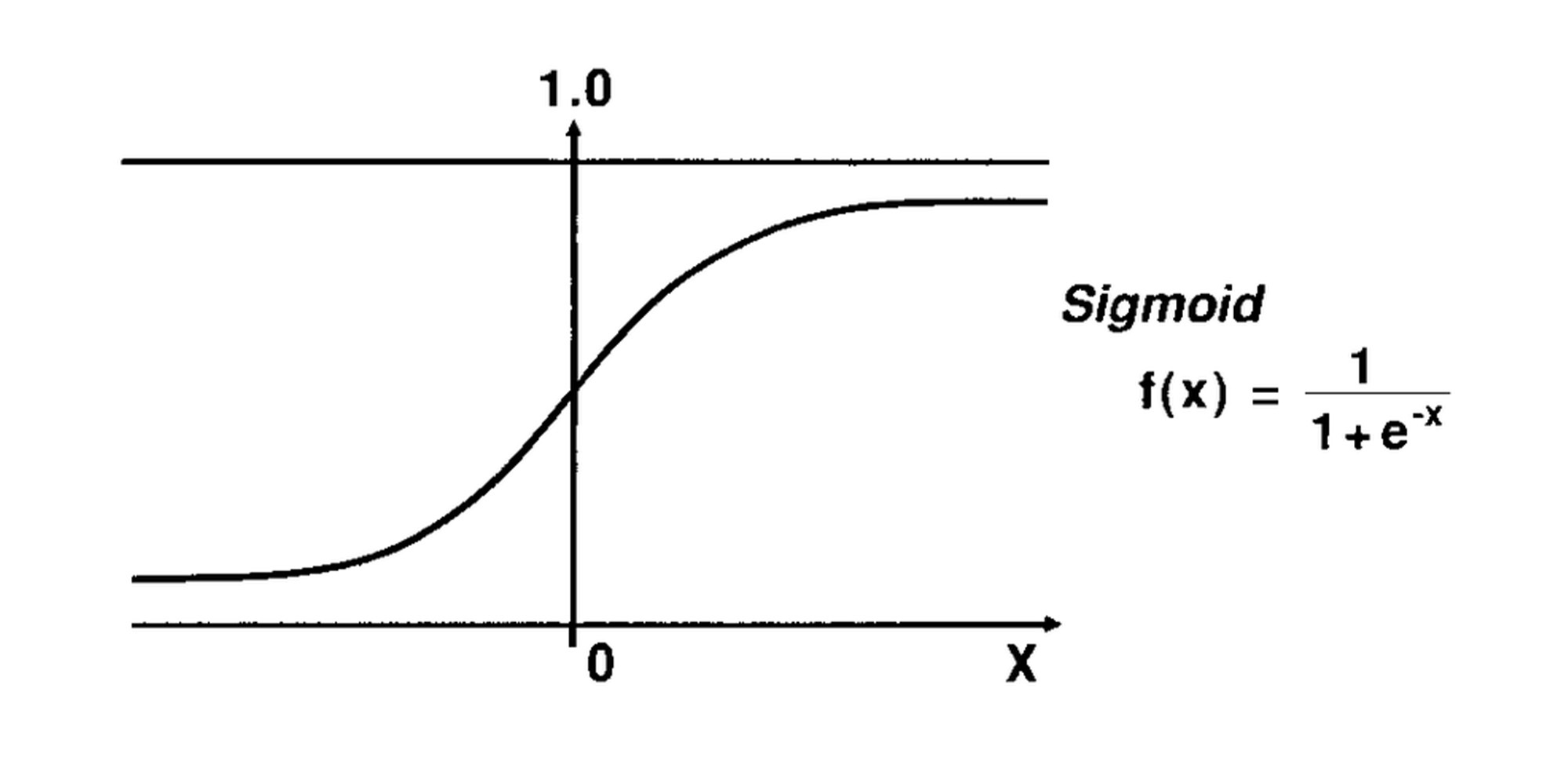
我们以会员是否流失为例,如果Sigmoid函数转化之后的预测结果值为0.7,就说明流失的概率大于0.5,可以认为该会员可能会流失。如果Sigmoid函数转化之后的预测结果值为0.4,就说明该会员留存的可能性比较高。对于其它的二元分类判断,比如病患是否患病、客户是否存在欺诈行为等等,都是同样的道理。
明白了这一点后,我们就用逻辑回归算法来预测一下“易速鲜花”的哪些客户流失风险比较高。首先,我们导入逻辑回归算法,并创建逻辑回归模型,我把模型命名为logreg(即LogisticRegression的缩写):
from sklearn.linear_model import LogisticRegression #导入逻辑回归模型
logreg = LogisticRegression() # lr,就代表是逻辑回归模型
然后,我们通过fit方法,开展对机器的训练:
logreg.fit(X_train,y_train) #拟合模型
模型拟合好之后,我们就可以对模型的分数进行评估了。
print("SK-learn逻辑回归测试准确率{:.2f}%".format(logreg.score(X_test,y_test)*100)) #模型分数
注意,这里的score方法给出的是预测准确率的均值。
输入如下:
SK-learn逻辑回归测试准确率78.70%
结果显示,这个逻辑回归模型在测试集上的准确率为78.70%。
最后,我们用这个模型来预测具体的用户是否会流失,我们选择测试集的第一个用户查看结果。
y_pred = logreg.predict(X_test) #对测试集进行预测
print("测试集第一个用户预测结果", y_pred[0]) #第一个用户预测结果
输出如下:
测试集第一个用户预测结果 0
我们得到的结果是0,说明这个逻辑回归模型判断第一个用户并不会流失,这个预测结果与真值一致。
这个模型看起来好像还不错,我们是不是可以把它应用于会员流失风险的评估呢?先别急,我们再来看看神经网络模型的表现如何。
你可能还在奇怪,我们已经用神经网络模型解决过问题了,为什么这里还要选择它呢?没错,在第11讲和第12讲中,我们用CNN完成了图像识别,用RNN完成了点击量的预测。不过,我们还没有使用普通的神经网络模型来解决分类问题。
相对于逻辑回归以及其它的分类算法,神经网络适合解决特征数量比较多、数据集样本数量庞大的分类问题,因为神经网络结构复杂,它的拟合能力当然也就比较强。所以,神经网络是我们解决分类问题时一个不错的选择。
怎么理解呢?这要从最早的神经网络说起。1958年,Rosenblatt提出了一种一元的“感知器”(Perceptron)模型,这是一种单个神经元的神经网络,也是最基本、最简单的神经网络,它的结构如下图所示:
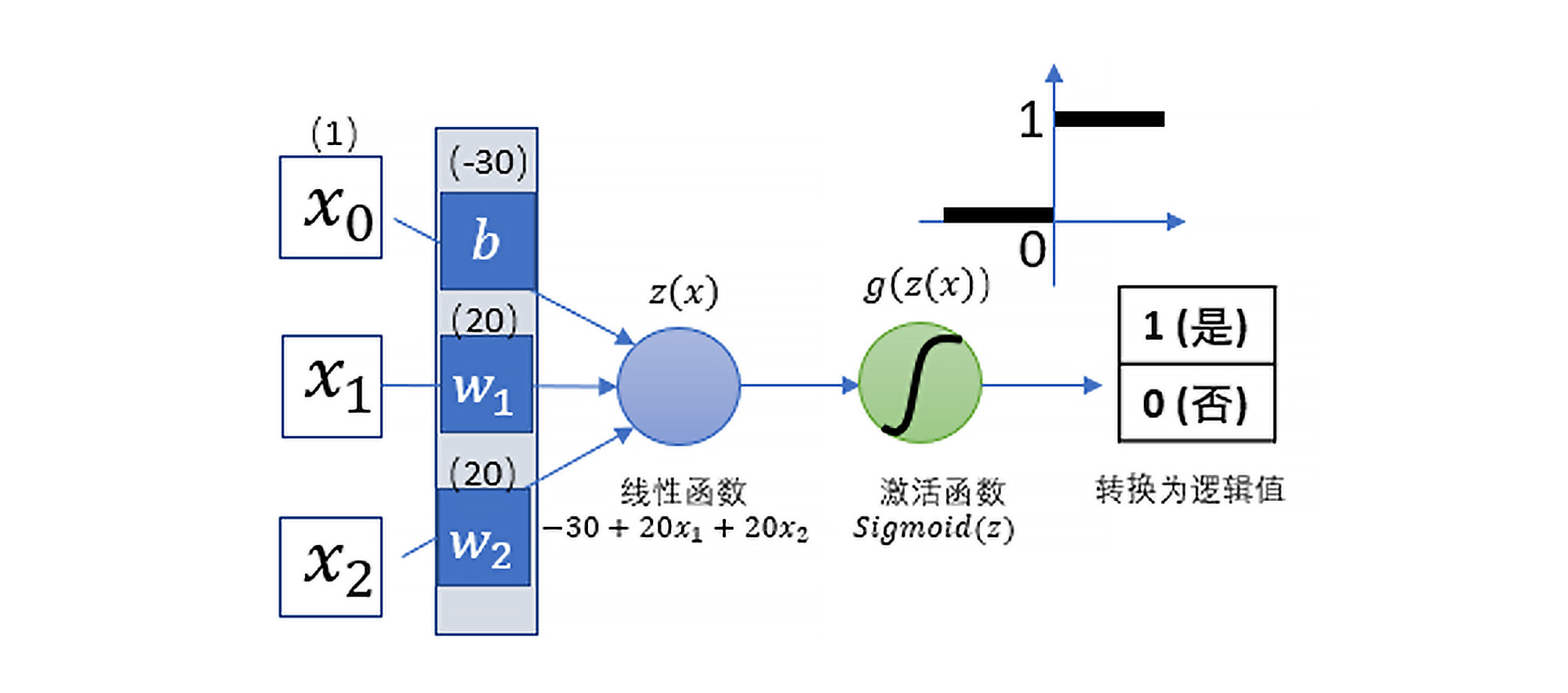
你看,这种一元的感知器从整体上是先接收特征的输入,然后做线性回归,进而通过Sigmoid函数求出分类概率,最后转化为分类值。 它实际上就是一个逻辑回归模型。所以,你可以认为,最基本、最简单的神经网络就是逻辑回归模型。
当然,现代神经网络已经演化成了具有很多层的深度学习网络,每一层也有非常多的类型,它们能够解决的问题也就更复杂了。但是,无论是浅层神经网络,还是深层神经网络,它们的网络结构都可以细分并简化为多个“一元感知器”,所以,现代的神经网络也都能够很好地解决二元分类问题。
现在回到我们的项目,请你思考一个问题,既然我们要预测一下“易速鲜花”的哪些客户流失风险比较高,那什么样的神经网络模型比较合适呢?我们之前学过CNN和RNN,它们合适吗?我们说,CNN网络主要用来处理图形图像等计算机视觉问题,RNN网络主要是处理自然语言、文字和时序问题。而我们当前这个数据具有很好的特征结构,它不是图片、文本,也不是时序数据,因此,它不需要CNN,也不需要RNN。
在这里呢,我们其实用普通的Dense层,也就是密集连接层,来搭建神经网络就可以了。Dense层是最普通的全连接网络层,因为它其中既没有卷积,也没有循环。而这样的神经网络我们叫它DNN。DNN网络非常适合解决分类问题,尤其是特征比较多的情况。
那DNN的网络结构是什么样的呢?别着急,我们先把这个模型构建起来,再一探究竟。由于数据集不大,这次实战并不需要GPU的出场,所以,我们直接在Jupyter Notebook上跑神经网络模型就可以了。
首先,我们安装Keras和Tensorflow这两个神经网络框架:
!pip install keras
!pip install tensorflow
安装过程输出如下:
Collecting keras
......
Successfully installed keras 2.6.0
......
Collecting tensorflow
Downloading tensorflow-2.6.0-cp38-cp38-win_amd64.whl (423.2 MB)
......
Successfully installed absl-py-0.13.0 astunparse-1.6.3 cachetools-4.2.
......
下面就开始搭建DNN神经网络模型:
import keras # 导入Keras库
from keras.models import Sequential # 导入Keras序贯模型
from keras.layers import Dense # 导入Keras密集连接层
dnn = Sequential() # 创建一个序贯DNN模型
dnn.add(Dense(units=12, input_dim=17, activation = 'relu')) # 添加输入层
dnn.add(Dense(units=24, activation = 'relu')) # 添加隐层
dnn.add(Dense(units=1, activation = 'sigmoid')) # 添加输出层
dnn.summary() # 显示网络模型(这个语句不是必须的)
# 编译神经网络,指定优化器,损失函数,以及评估标准
dnn.compile(optimizer = 'RMSProp', #优化器
loss = 'binary_crossentropy', #损失函数
metrics = ['acc']) #评估标准
DNN神经网络的结构输出如下:
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 12) 228
_________________________________________________________________
dense_1 (Dense) (None, 24) 312
_________________________________________________________________
dense_2 (Dense) (None, 1) 25
=================================================================
Total params: 565
Trainable params: 565
Non-trainable params: 0
_________________________________________________________________
可以看到,这个DNN神经网络的结构和我们之前见过的CNN和RNN大同小异,唯一的区别就在于,我们这里使用的是Dense层。
另外,在编译时,损失函数、优化器和评估指标的选择也不太一样。其中,我们把损失函数指定为binary_crossentropy,这是专门用来二分类问题的损失函数;而对于优化器,我们选择的是RMSProp;评估指标则是Accuracy(分类准确率)。
如果你仔细看上面搭建DNN网络模型的代码,可能会留意到:前两个Dense层的activation值为relu,而最后一层是sigmoid。这是什么意思呢?
其实,这里的activation就是神经网络的激活函数。激活函数在神经网络中是用来引入非线性因素的,目的是提升模型的表达能力。否则的话,各层神经元之间只存在线性关系,这种模型的表达能力就不够强,不能覆盖更复杂的特征空间,因此神经网络的每一个神经元,在向下一层网络输出特征时都需要用激活函数进行激活。
在早期的神经网络中,神经元全都是使用sigmoid函数作为激活函数的,后来又出现了和sigmoid函数类似的tanh函数。不过,人们发现,当输入的特征值较大时,tanh函数的梯度(导数)接近于零,这时参数几乎不再更新,梯度的反向传播过程将被中断,可能会出现梯度消失的现象,而这会影响神经网络的性能。
这里所说的“反向传播”,就是指在神经网络的梯度下降中,从后面的层向前面层传播的过程(神经网络中,既有从前面层向后面层的传播,也有从后面的层向先前面层的传播)。
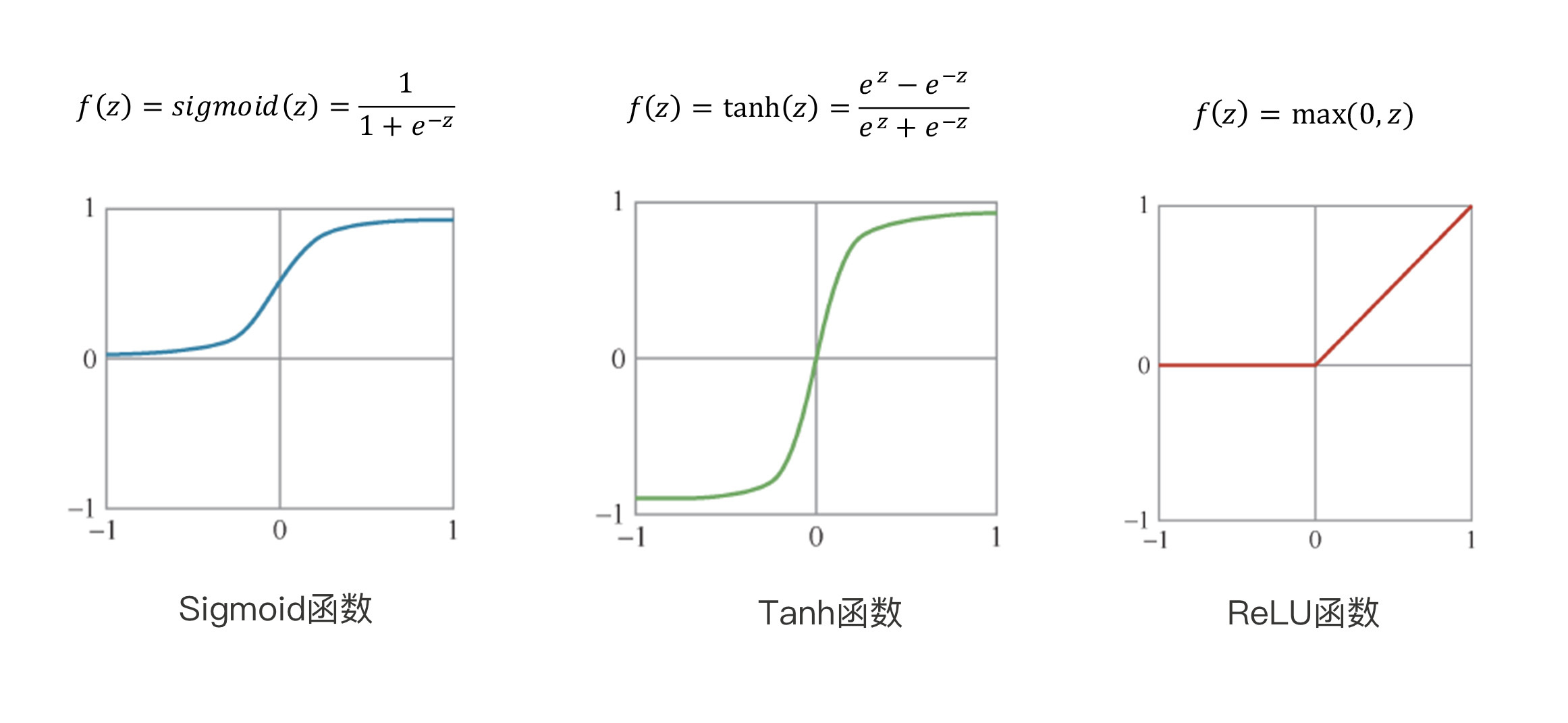
再后来,人们发现了一个更好的神经元激活函数:ReLU函数。它实现起来非常简单,不仅加速了梯度下降的收敛过程,而且还没有饱和问题,这大大缓解了梯度消失的现象。
不过,ReLU函数也不是完全没有缺点,在某些情况下,如果参数的权重都处于负值区间,ReLU函数对损失函数的导数可能永远为零。这个神经元将永远不参与整个模型的学习过程,等同于“死掉”。
为了解决这个问题,人们又发明了Leaky ReLU、eLu、PreLu、Parametric ReLU、Randomized ReLU等变体,为ReLU函数在负区间赋予一定的斜率,从而让它的导数不为零。不过,对于我们初学者来说,不需要深入掌握这些变体的区别和用法,我们一般使用ReLU函数激活就可以了,它也是目前普通神经网络中最常用的激活函数。
上面所说的激活过程,只是针对于神经网络内部的神经元而言的。而对于神经网络的输出层来说,激活函数的作用就只是确定分类概率了。
我们知道,概率必须是一个0~1之间的值,这时候,ReLU等函数就无法发挥作用了。所以,如果是二元分类问题,我们在神经网络的输出层中会使用sigmoid函数来进行分类激活;如果是多元分类问题,我们则使用softmax函数进行分类激活。
搞清楚了DNN网络模型的结构后,现在我们开始进行神经网络的训练。不过,在开始训练之前,我们要做一下格式的转换,把Dataframe格式的对象转换为NumPy张量。关于张量,我们在第11讲中介绍过,这里就不重复了。
X_train = np.asarray(X_train).astype(np.float32) # 转换为NumPy张量
X_test = np.asarray(X_test).astype(np.float32) # 转换为NumPy张量
history = dnn.fit(X_train, y_train, # 指定训练集
epochs=30, # 指定训练的轮次
batch_size=64, # 指定数据批量
validation_split=0.2) #这里直接从训练集数据中拆分验证集,更方便
训练过程输出如下:
Epoch 1/30
71/71 [==============================] - 1s 6ms/step - loss: 4.1202 - acc: 0.6761 - val_loss: 2.9610 - val_acc: 0.4632
Epoch 2/30
71/71 [==============================] - 0s 3ms/step - loss: 1.1665 - acc: 0.7182 - val_loss: 0.8802 - val_acc: 0.6016
Epoch 3/30
71/71 [==============================] - 0s 2ms/step - loss: 1.1551 - acc: 0.7087 - val_loss: 2.1645 - val_acc: 0.7773
......
Epoch 29/30
71/71 [==============================] - 0s 3ms/step - loss: 0.8423 - acc: 0.7495 - val_loss: 1.3655 - val_acc: 0.7862
Epoch 30/30
71/71 [==============================] - 0s 3ms/step - loss: 0.8477 - acc: 0.7404 - val_loss: 1.1125 - val_acc: 0.7977
这个训练信息不够直观,我们要做个处理。不知道你记不记得在第11讲中,我们介绍过显示损失曲线和准确率曲线的方法,现在我们就用这个方法看一看在上述训练过程中,随着梯度的下降和模型的拟合,损失和准确率在训练集和验证集上的变化情况:
def show_history(history): # 显示训练过程中的学习曲线
loss = history.history['loss'] #训练损失
val_loss = history.history['val_loss'] #验证损失
epochs = range(1, len(loss) + 1) #训练轮次
plt.figure(figsize=(12,4)) # 图片大小
plt.subplot(1, 2, 1) #子图1
plt.plot(epochs, loss, 'bo', label='Training loss') #训练损失
plt.plot(epochs, val_loss, 'b', label='Validation loss') #验证损失
plt.title('Training and validation loss') #图题
plt.xlabel('Epochs') #X轴文字
plt.ylabel('Loss') #Y轴文字
plt.legend() #图例
acc = history.history['acc'] #训练准确率
val_acc = history.history['val_acc'] #验证准确率
plt.subplot(1, 2, 2) #子图2
plt.plot(epochs, acc, 'bo', label='Training acc') #训练准确率
plt.plot(epochs, val_acc, 'b', label='Validation acc') #验证准确率
plt.title('Training and validation accuracy') #图题
plt.xlabel('Epochs') #X轴文字
plt.ylabel('Accuracy') #Y轴文字
plt.legend() #图例
plt.show() #绘图
show_history(history) # 调用这个函数
输出如下:
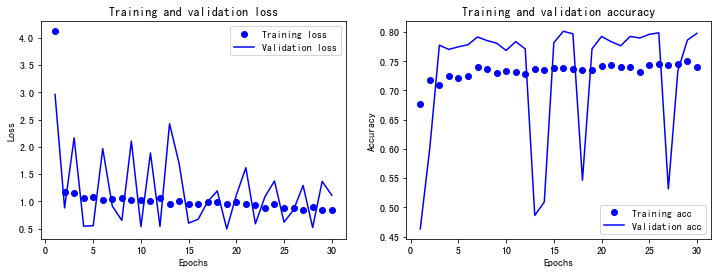
从图中可见,训练集的损失逐渐下降,准确率逐渐提升。但是,验证集的曲线不那么漂亮,有振荡的情况,这种情况意味着网络没有训练起来。接下来,我们还是看一看它在测试集上的准确率是否理想吧:
result = dnn.evaluate(X_test, y_test) #评估测试集上的准确率
print('DNN的测试准确率为',"{0:.2f}%".format(result[1])*100)
输出如下:
45/45 [==============================] - 0s 1ms/step - loss: 1.0171 - acc: 0.7658
DNN的测试准确率为 77%
再看看第一个测试集用户的预测结果:
prediction = dnn.predict(X_test) #预测测试集的图片分类
print('第一个用户分类结果为:', np.argmax(prediction[0]))
输出如下:
第一个用户分类结果为: 0
0值代表客户未流失,说明这个神经网络模型预测该用户并不会流失,与真值相符。
那这个模型到底满不满足我们的需求呢?其实,我们还是不能确定。这个问题我们暂且放在一边,后续再做探讨。
现在,我想请你思考一下,DNN神经网络模型在测试集上的预测准确率达到了77%,表面上还可以。但是,损失曲线和准确率曲线图却显示,这个模型的损失和准确率都出现了很大的振荡波动,时好时坏。这又是什么原因呢?
其实,这种振荡现象的出现是数据所造成的。我们之前说过,神经网络非常不喜欢未经归一化的数据,因此,对于神经网络来说,我们前面对这个数据集做预处理时,可能缺少了一个环节,就是归一化。
下面,我们就把应该做的对X特征集的归一化工作给补上:
from sklearn.preprocessing import MinMaxScaler #导入归一化缩放器
scaler = MinMaxScaler() #创建归一化缩放器
X_train = scaler.fit_transform(X_train) #拟合并转换训练集数据
X_test = scaler.transform(X_test) #转换测试集数据
然后,我们仍然用同样DNN神经网络训练数据,并绘制损失曲线和准确率曲线:
history = dnn.fit(X_train, y_train, # 指定训练集
epochs=30, # 指定训练的轮次
batch_size=64, # 指定数据批量
validation_split=0.2) #指定验证集,这里为了简化模型,直接用训练集数据
show_history(history) # 调用这个函数
输出如下:
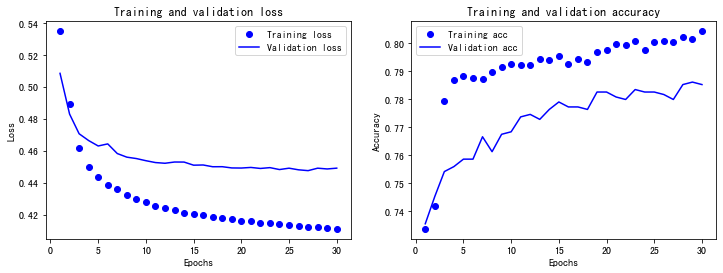
结果显示,振荡现象消失了,曲线的变得平滑了很多,这是神经网络能够正常训练起来的一种表现:
最后,我们看一下新的神经网络模型的测试准确率。
result = dnn.evaluate(X_test, y_test) #评估测试集上的准确率
print('DNN(归一化之后)的测试准确率为',"{0:.2f}%".format(result[1])*100)
输出如下:
45/45 [==============================] - 0s 2ms/step - loss: 78.6179 - acc: 0.7800
DNN(归一化之后)的测试准确率为 78%
可以看到,归一化后的测试准确率为78%,比起刚才的77%,基本没什么差别。
到这里,我们针对“预测哪些客户流失风险比较高”这个任务,产出了三个模型:逻辑回归模型、未做归一化的神经网络模型DNN,以及归一化之后的神经网络模型DNN。那这三种模型是不是都符合我们的需求呢?哪一种模型更好呢?你可以思考一下,在下一讲中,我会为你揭晓答案。
这节课,我们用逻辑回归和深度学习神经网络预测了“易速鲜花”的会员是否会流失,这是一个典型的二元分类问题。二元分类是很常见的一类监督学习问题,能够用于解决二元分类问题的算法也非常多,包括逻辑回归、朴素贝叶斯、KNN等等。
逻辑回归是解决二元分类问题最简单的方法,它的实现也比较简单,就是从sklearn中导入、创建并拟合逻辑回归模型,方法与我们在前面几关中的步骤完全相同。
值得一提的是,在解决二元分类问题时,我们可以通过logreg.predict()函数来预测分类的值,也可以通过logreg.predict_proba()函数来输出分类的概率,概率越高,模型就认为归为该类可能性越大。举例来说,0.51和0.99两个概率值,模型都预测用户会流失,但是有多大的信心?明显概率为0.99的高得多。
在用神经网络解决二元分类问题时,我们选择了最普通的神经网络模型DNN,它的创建和训练过程与我们在第11讲到第13讲中的步骤并无区别。由于神经网络模型的predict()函数输出的是概率,如果你需要手工进行分类转化,可以用np.argmax函数来完成,这个步骤我们在第11讲也介绍过,你如果不太清楚,可以再复习一下。
最后,我还想强调一点,通过这一讲,我们已经看到,对于神经网络的输入张量,如果不做归一化,就会影响神经网络的训练效果。因此,我希望你能明白为神经网络输入张量做归一化的重要性。
好,这节课就到这里,我给你留两道思考题:
欢迎你在留言区和我分享你的观点,如果你认为这节课的内容有收获,也欢迎把它分享给你的朋友,我们下一讲再见!
