
这里的 P(至少出现一个第一类错误)的概率又叫做 FWER (Family-wise Error Rate)。
通过计算得出来的概率是64%。这就意味着当同时比较20个检验时,在这20个结果中,至少出现一个第一类错误的概率是64%。看看,这是不是个很大的概率了呢?事实上,随着检验次数的增加,这个概率会越来越大,你看看下面这个图就明白了。
你好,我是博伟。
上节课,我们讲了一个在做A/B测试时普遍存在的一个问题,那么接下来,我就根据自己这些年做A/B测试的经验,精选了一些在实际业务中会经常遭遇的误区,主要是多重检验问题、学习效应、辛普森悖论和实验/对照组的独立性这四大误区。
这四个误区,其实也可以被看作在实际业务中经常出现的几个问题。不过我在题目中之所以强调说这是误区,是因为你很可能会在这些问题的理解上产生一些偏差。
所以接下来我在讲这两节课时,会按照“问题阐述—问题解析—总结引申—课后思考”的范式来给你讲。也就是说,我会先带你深入剖析问题的成因,然后再举例分析这些问题在实践中的表现形式,最后给出对应的解决方法。
毕竟,在搞清楚问题原理的前提下,再学习问题的表现形式和解决方法,不仅你的学习效果会事半功倍,而且在实际应用时,你也能根据变化多端的业务场景,随机应变,灵活运用。
多重检验问题,又叫多重测试问题或多重比较问题(Multiple Comparison Problem),指的是当同时比较多个检验时,第一类错误率α就会增大,而结果的准确性就会受到影响这个问题。我在基础篇讲A/B测试流程时就多次提到过它,比如第4节课讲OEC的好处时,还有第7节课讲什么时间才能查看测试结果时。
要搞清楚多重检验为什么会是一个问题,我们还得先从第一类错误率α(又叫假阳性率,显著水平,是测试前的预设值,一般为5%)说起。我在第2节课也讲过,第一类错误率指的就是当事实上两组指标是相同的时候,假设检验推断出两组指标不同的概率,或者说由于偶然得到显著结果的概率。而且,它在统计上的约定俗成是5%。
5%看上去是个小概率事件,但是如果我们同时比较20个检验(测试)呢?你可以先思考一下,如果每个检验出现第一类错误的概率是5%,那么在这20个检验中至少出现一个第一类错误的概率是多少呢?
要直接求出这个事件的概率不太容易,我们可以先求出这个事件发生情况的反面,也就是在这20个检验中完全没有出现第一类错误的概率,然后再用100%减去这个反面事件的概率。
这里我们用P(A)来表示出现事件A的概率。P(每个检验出现第一类错误)=5%,那么P(每个检验不出现第一类错误) = (1-5%)=95%,所以P(20个检验中完全没有第一类错误)= 95%的20次方。
这样我们就可以求得这个概率:

这里的 P(至少出现一个第一类错误)的概率又叫做 FWER (Family-wise Error Rate)。
通过计算得出来的概率是64%。这就意味着当同时比较20个检验时,在这20个结果中,至少出现一个第一类错误的概率是64%。看看,这是不是个很大的概率了呢?事实上,随着检验次数的增加,这个概率会越来越大,你看看下面这个图就明白了。
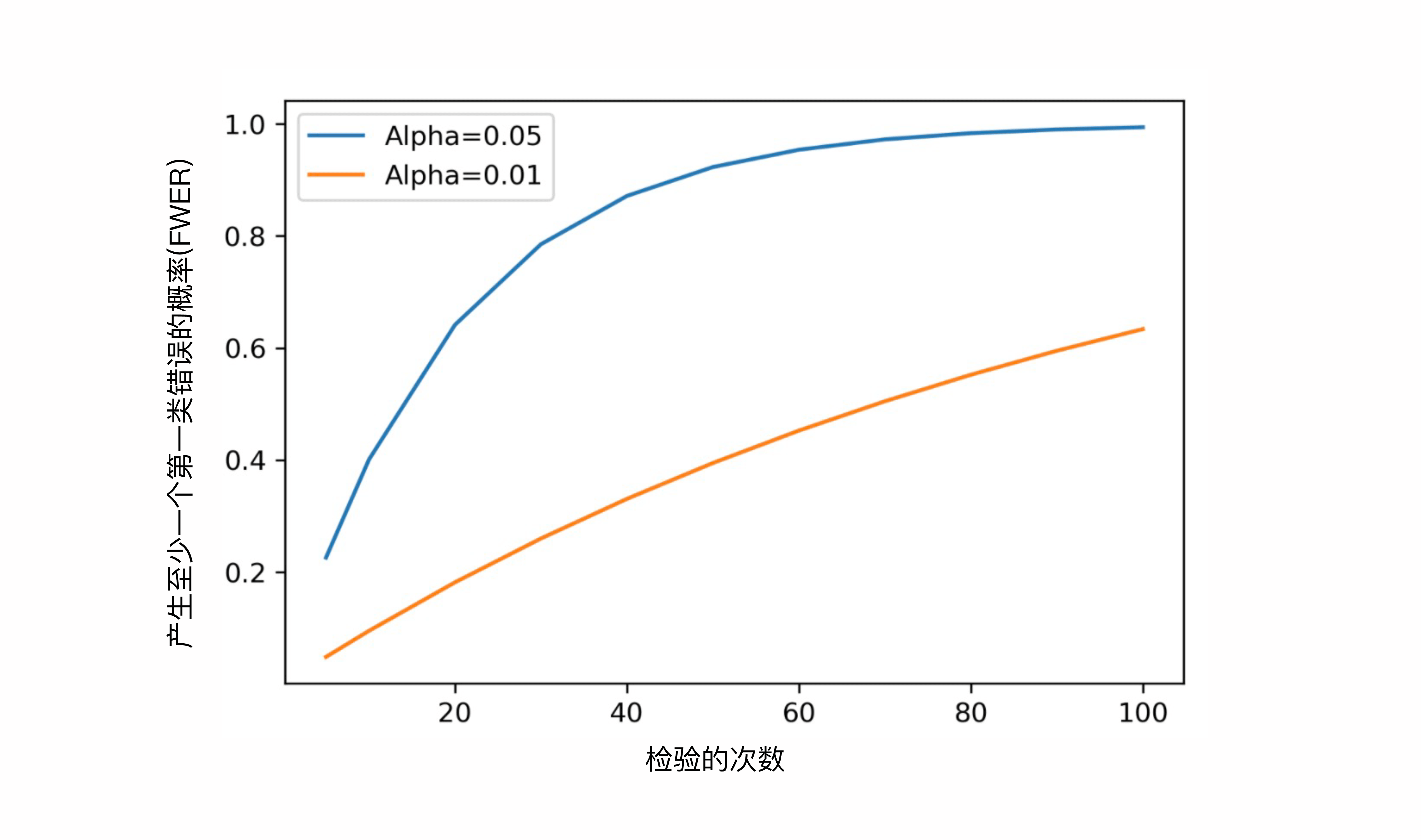
图中的蓝线和橙线分别表示当α=5%和1%时,FWER的变化情况。根据这个图我们可以得出两个结论:
随着检验次数的增加,FWER,也就是出现第一类错误的概率会显著升高。
当α越小时,FWER会越小,上升的速度也越慢。
第一个结论讲的就是多重检验带来的问题。第二个结论其实为我们提供了一种潜在的解决方法:降低α。
这就意味着,当我们同时比较多个检验时,就增加了得到第一类错误的概率(FWER),这就变成了一个潜在的多重检验问题。
你可能会说我平时都是一个测试一个测试去跑,不会同时跑多个测试,是不是就不会遇到这个问题了呢?其实不是的,实践中出现多重检验问题比你想象的要普遍得多,它在实践中主要以4种形式出现。
第一种形式,当A/B测试有不止一个实验组时。
当我们想要改变不止一个变量且样本量充足时,我们可以不必等测试完一个变量后再去测试下一个,而是可以同时测试这些变量,把它们分在不同的实验组当中。
每个实验组只变化一个变量,在分析结果时分别用每个实验组和共同的对照组进行比较,这种测试方法也叫做A/B/n测试。比如我想要改变广告来提升其效果,那么想要改变的变量包括内容、背景颜色、字体大小等等,这个时候我就要有相对应的3个实验组,然后把它们分别和对照组进行比较。
这就相当于同时进行了3个检验,就会出现多重检验问题。
第二种形式,当A/B测试有不止一个评价指标时。
这个很好理解,因为我们分析测试结果,其实就是比较实验组和对照组的评价指标。如果有多个评价指标的话,就会进行多次检验,产生多重检验问题。
第三种形式,当你在分析A/B测试结果,按照不同的维度去做细分分析(Segmentation Analysis)时。
当我们分析测试结果时,根据业务需求,有时我们并不满足于只把实验组和对照组进行总体比较。
比如对于一个跨国公司来说,很多A/B测试会在全球多个国家同时进行,这时候如果我们想要看A/B测试中的变化对于各个国家的具体影响时,就会以国家为维度来做细分的分析,会分别比较单个国家中的两组指标大小,那么此时分析每个国家的测试结果就是一个检验,多个国家则是多个检验。
第四种形式,当A/B测试在进行过程中,你不断去查看实验结果时。
这种情况我在第7节课中提到过,因为当测试还在进行中,所以每次查看的测试都和上一次的不一样,每查看一次结果都算是一次检验,这样也会产生多重检验问题。
了解了多重检验问题在实践中的表现形式,那么在实践中该如何解决它呢?
首先我要提前说明的是,接下来我介绍的解决方法,只适用于前3种表现形式。对于第4种表现形式的解决办法,我已经在第7节课介绍了,那就是不要在A/B测试还在进行时就过早地去查看结果,一定要等样本量达到要求后再去计算结果,所以这里就不再赘述。
鉴于多重检验问题的普遍性,在统计上有很多学者提出了自己的解决方法,大致分为两类:
保持每个检验的P值不变,调整α。
保持α不变,调整每个检验的P值。
为什么会做这两种调整呢?
在第2节课,我们介绍了用P值来判断假设检验的结果是否显著时,是用检验中计算出的P值和α进行比较的。当P值<α时,我们才说结果显著。
所以,我们要么调整α,要么调整P值。前面我也说了,降低α是一种解决办法,最常用的调整α的方法是Bonferroni校正(Bonferroni Correction),其实很简单,就是把α变成α/n。
其中n是检验的个数。比如α=5%,那当我们比较20个检验时,校正之后的α=5%/20 = 0.25%,此时的FWER =$1-(1-0.25 \%)^{20}$ = 4.88% ,和我们最初设定的α=5%差不多。
Bonferroni校正由于操作简单,在A/B测试的实践中十分流行,但是这种方法只是调整了α,对于不同的P值都采取了一刀切的办法,所以显得有些保守,检测次数较少时还可以适用。
根据实践经验,在检测次数较大时(比如上百次,这种情况在A/B测试中出现的情况一般是做不同维度的细分分析时,比如对于跨国公司来说,有时会有上百个markets), Bonferroni校正会显著增加第二类错误率β,这时候一个比较好的解决办法就是去调整P值,常用的方法就是通过控制FDR(False Discovery Rate)来实现。
控制FDR的原理比较复杂,我就不展开讲了,你只需要记住它指的是一类方法,其中最常用的是BH法(Benjamini-Hochberg Procedure)就行了。BH法会考虑到每个P值的大小,然后做不同程度的调整。大致的调整方法就是把各个检验计算出的P值从小到大排序,然后根据排序来分别调整不同的P值,最后再用调整后的P值和α进行比较。
实践中,我们一般会借助像Python这样的工具来计算,Python中的multipletests函数很强大,里面有各种校正多重检验的方法,其中就包括我们今天讲的Bonferroni校正和BH法,我们使用时只需要把不同的P值输入,选取校正方法,这个函数就会给我们输出校正后的P值。
这里我总结一下,虽然Bonferroni校正十分简单,但由于过于严格和保守,所以在实践中我会更推荐使用BH法来矫正P值。
聊完了多重检验问题,我们再聊一下A/B测试中另一个常见问题——学习效应。
当我们想通过A/B测试检验非常明显的变化时,比如改变网站或者产品的交互界面和功能,那些网站或者产品的老客户往往适应了之前的交互界面和功能,而新的交互界面和功能对他们来说需要一段时间来适应和学习。所以往往老用户在学习适应阶段的行为会跟平时有些不同,这就是学习效应。
根据不同的改变,老用户在学习适应期的反应也不同,一般分为两种。
第一种是积极的反应,一般也叫做新奇效应(Novelty Effect),指的是老用户对于变化有很强的好奇心,愿意去尝试。
比如把点击按钮的颜色,由之前的冷色调变成了非常艳丽的大红色,在短期内可能会使诸如点击率之类的指标提升,但是当用户适应了新的大红色后,长期的指标也可能回归到之前的水平。
第二种是消极的反应,一般也叫做改变厌恶(Change Aversion)。指的是老用户对于变化比较困惑,甚至产生抵触心理。
比如你经常光顾的电商网站,之前的加入购物车功能是在屏幕的左上方,但是交互界面改变后加入购物车的位置变到了屏幕的右下方,这个时候你可能就需要在屏幕上找一阵子才能找到,甚至找了一圈没找到,因为烦躁就关掉了页面,那么这时候短期的指标就会下降。
可以想象,这些在学习适应期的不同反应一般是短期的,长期来看这些短期反应也是会慢慢消退的。但是要注意的是,这些短期的学习效应确实会给A/B测试的结果带来干扰,使结果变得过于好或者过于差。那么我们如何来及时发现学习效应,从而剔除学习效应带来的干扰呢?
在实践中,主要有两种方法可以用来检测学习效应。
第一种方法是表征实验组的指标随着时间(以天为单位)的变化情况。
在没有学习效应的情况下,实验组的指标随着时间的变化是相对稳定的。
但是当有学习效应时,因为学习效应是短期的,长期来看慢慢会消退,那么实验组(有变化的组)的指标就会有一个随着时间慢慢变化的过程,直到稳定。
当然我们在使用这个方法时需要注意:随着时间表征实验组的指标变化,但并不是让你每天去比较实验组和对照组的大小。如果每天都去比较,就会出现我们刚才讲的多重检验的问题。一定要记住,只有达到样本量之后才可以去比较两组大小,分析测试结果。
第二种方法是只比较实验组和对照组中的新用户。
学习效应是老用户为了学习适应新的变化产生的,所以对于新用户,也就是在实验期间才第一次登录的用户来说,并不存在“学习适应新的变化”这个问题,那么我们可以先在两组找出新用户(如果是随机分组的话,两组中新用户的比例应该是相似的),然后只在两组的新用户中分别计算我们的指标,最后再比较这两个指标。
如果我们在新用户的比较中没有得出显著结果(在新用户样本量充足的情况下),但是在总体的比较中得出了显著结果,那就说明这个变化对于新用户没有影响,但是对于老用户有影响,那么大概率是出现了学习效应。
在实践中我们可以用以上方法检测出学习效应,不过要想真正排除学习效应的影响,得到准确的实验结果,还是要延长测试时间,等到实验组的学习效应消退再来比较两组的结果。
今天这节课我们重点讲解了A/B测试中两个常见的实验误区:多重检验问题和学习效应。我把这两个问题出现的原理、在实践中的多种表现形式,以及相应的解决方法,都给你详细讲解了。
不过我还想特别强调一下多重检验问题。多重检验问题的表现形式多种多样,所以在A/B测试中尤为常见。我在刚接触A/B测试时就已经知道了这个问题的存在,不过当时了解到的是它会在A/B/n测试中出现,但后来才发现,原来在做细分分析时也会出现多重检验的问题。
幸好这个问题发现得及时,才没有让整个测试功亏一篑。现在再去复盘,主要还是因为当时只知道多重检验问题的存在,了解其中一两个表现形式。但对于为什么会出现多重检验问题,什么时候可能会出现多重检验问题,我都不清楚,所以在问题出现新的表现形式时就没有及时识别出来。
这也是我想要跟你强调的,知道为什么会出现这个问题,并且发现问题,和解决问题同样重要。
思考题
结合自己的经验,想一想过去有没有在A/B测试中遇到多重检验问题和学习效应?以及当时是如何处理的呢?
欢迎在评论区写下你学习本节课的收获和深度思考,如果今天的内容能帮你解答了一些困惑问题,也欢迎点击“请朋友读”,和他一起学习、成长。感谢你的收听,我们下节课再见。