你好,我是蒋德钧。
有序集合(Sorted Set)是Redis中一种重要的数据类型,它本身是集合类型,同时也可以支持集合中的元素带有权重,并按权重排序。
而曾经就有一位从事Redis开发的同学问我:为什么Sorted Set能同时提供以下两种操作接口,以及它们的复杂度分别是O(logN)+M和O(1)呢?
实际上,这个问题背后的本质是:为什么Sorted Set既能支持高效的范围查询,同时还能以O(1)复杂度获取元素权重值?
这其实就和Sorted Set底层的设计实现有关了。Sorted Set能支持范围查询,这是因为它的核心数据结构设计采用了跳表,而它又能以常数复杂度获取元素权重,这是因为它同时采用了哈希表进行索引。
那么,你是不是很好奇,Sorted Set是如何把这两种数据结构结合在一起的?它们又是如何进行协作的呢?今天这节课,我就来给你介绍下Sorted Set采用的双索引的设计思想和实现。理解和掌握这种双索引的设计思想,对于我们实现数据库系统是具有非常重要的参考价值的。
好,接下来,我们就先来看看Sorted Set的基本结构。
要想了解Sorted Set的结构,就需要阅读它的代码文件。这里你需要注意的是,在Redis源码中,Sorted Set的代码文件和其他数据类型不太一样,它并不像哈希表的dict.c/dict.h,或是压缩列表的ziplist.c/ziplist.h,具有专门的数据结构实现和定义文件。
Sorted Set的实现代码在t_zset.c文件中,包括Sorted Set的各种操作实现,同时Sorted Set相关的结构定义在server.h文件中。如果你想要了解学习Sorted Set的模块和操作,注意要从t_zset.c和server.h这两个文件中查找。
好,在知道了Sorted Set所在的代码文件之后,我们可以先来看下它的结构定义。Sorted Set结构体的名称为zset,其中包含了两个成员,分别是哈希表dict和跳表zsl,如下所示。
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
在这节课一开始,我就说过Sorted Set这种同时采用跳表和哈希表两个索引结构的设计思想,是非常值得学习的。因为这种设计思想充分利用了跳表高效支持范围查询(如ZRANGEBYSCORE操作),以及哈希表高效支持单点查询(如ZSCORE操作)的特征。这样一来,我们就可以在一个数据结构中,同时高效支持范围查询和单点查询,这是单一索引结构比较难达到的效果。
不过,既然Sorted Set采用了跳表和哈希表两种索引结构来组织数据,我们在实现Sorted Set时就会面临以下两个问题:
因为我已经在第3讲中给你介绍了Redis中哈希表的实现思路,所以接下来,我主要是给你介绍下跳表的设计和实现。通过学习跳表,你可以了解到跳表中保存的数据,以及跳表的常见操作。然后,我再带你来探究下Sorted Set如何将哈希表和跳表组合起来使用的,以及这两个索引结构中的数据是如何保持一致的。
首先,我们来了解下什么是跳表(skiplist)。
跳表其实是一种多层的有序链表。在课程中,为了便于说明,我把跳表中的层次从低到高排个序,最底下一层称为level0,依次往上是level1、level2等。
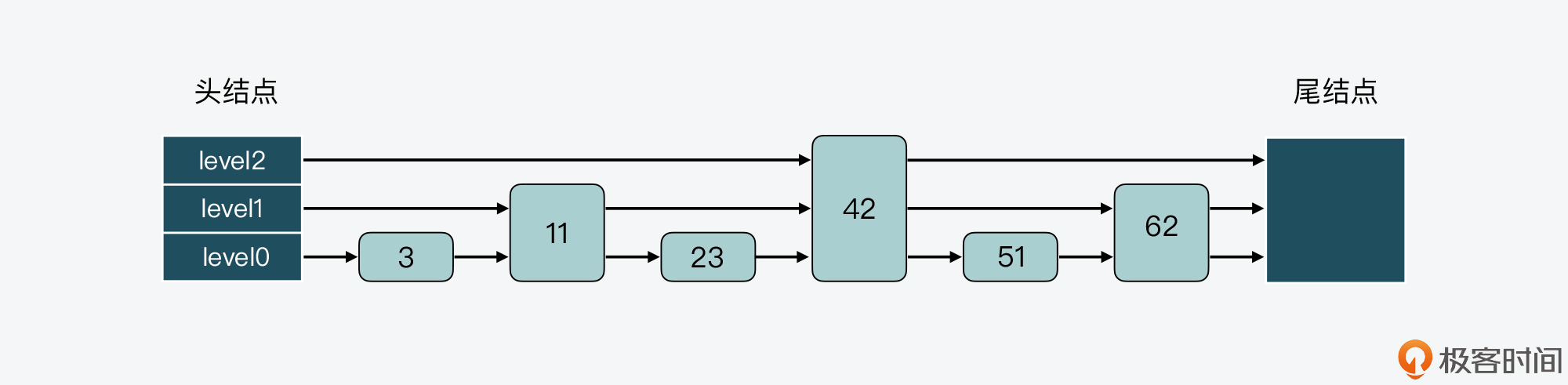
下图展示的是一个3层的跳表。其中,头结点中包含了三个指针,分别作为leve0到level2上的头指针。

可以看到,在level 0上一共有7个结点,分别是3、11、23、33、42、51、62,这些结点会通过指针连接起来,同时头结点中的level0指针会指向结点3。然后,在这7个结点中,结点11、33和51又都包含了一个指针,同样也依次连接起来,且头结点的level 1指针会指向结点11。这样一来,这3个结点就组成了level 1上的所有结点。
最后,结点33中还包含了一个指针,这个指针会指向尾结点,同时,头结点的level 2指针会指向结点33,这就形成了level 2,只不过level 2上只有1个结点33。
好,在对跳表有了直观印象后,我们再来看看跳表实现的具体数据结构。
我们先来看下跳表结点的结构定义,如下所示。
typedef struct zskiplistNode {
//Sorted Set中的元素
sds ele;
//元素权重值
double score;
//后向指针
struct zskiplistNode *backward;
//节点的level数组,保存每层上的前向指针和跨度
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
首先,因为Sorted Set中既要保存元素,也要保存元素的权重,所以对应到跳表结点的结构定义中,就对应了sds类型的变量ele,以及double类型的变量score。此外,为了便于从跳表的尾结点进行倒序查找,每个跳表结点中还保存了一个后向指针(*backward),指向该结点的前一个结点。
然后,因为跳表是一个多层的有序链表,每一层也是由多个结点通过指针连接起来的。因此在跳表结点的结构定义中,还包含了一个zskiplistLevel结构体类型的level数组。
level数组中的每一个元素对应了一个zskiplistLevel结构体,也对应了跳表的一层。而zskiplistLevel结构体定义了一个指向下一结点的前向指针(*forward),这就使得结点可以在某一层上和后续结点连接起来。同时,zskiplistLevel结构体中还定义了跨度,这是用来记录结点在某一层上的*forward指针和该指针指向的结点之间,跨越了level0上的几个结点。
我们来看下面这张图,其中就展示了33结点的level数组和跨度情况。可以看到,33结点的level数组有三个元素,分别对应了三层level上的指针。此外,在level数组中,level 2、level1和level 0的跨度span值依次是3、2、1。
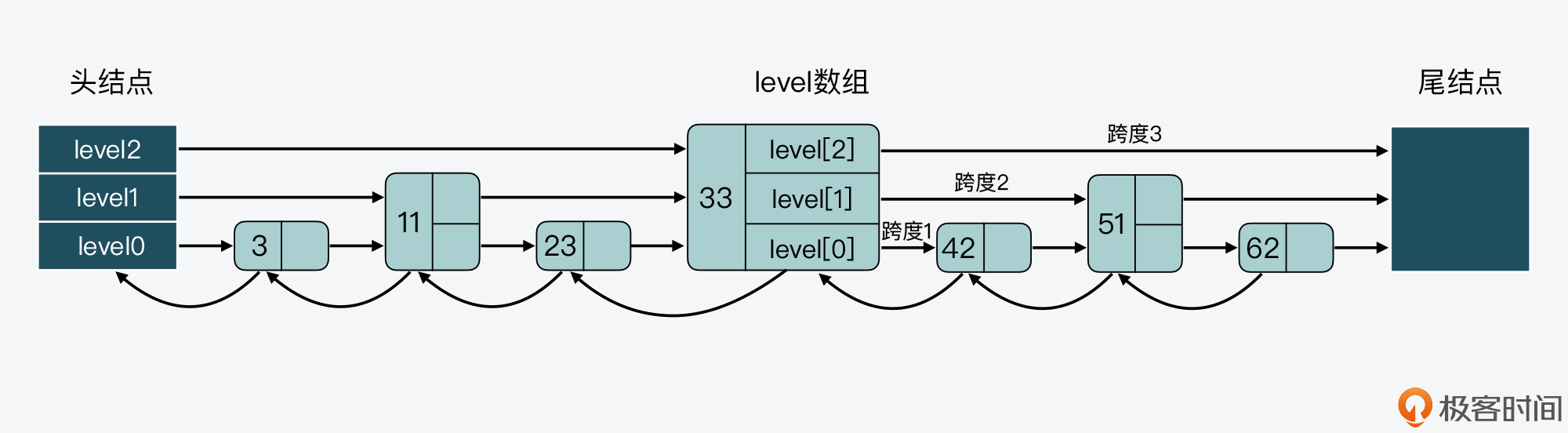
最后,因为跳表中的结点都是按序排列的,所以,对于跳表中的某个结点,我们可以把从头结点到该结点的查询路径上,各个结点在所查询层次上的*forward指针跨度,做一个累加。这个累加值就可以用来计算该结点在整个跳表中的顺序,另外这个结构特点还可以用来实现Sorted Set的rank操作,比如ZRANK、ZREVRANK等。
好,了解了跳表结点的定义后,我们可以来看看跳表的定义。在跳表的结构中,定义了跳表的头结点和尾结点、跳表的长度,以及跳表的最大层数,如下所示。
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
因为跳表的每个结点都是通过指针连接起来的,所以我们在使用跳表时,只需要从跳表结构体中获得头结点或尾结点,就可以通过结点指针访问到跳表中的各个结点。
那么,当我们在Sorted Set中查找元素时,就对应到了Redis在跳表中查找结点,而此时,查询代码是否需要像查询常规链表那样,逐一顺序查询比较链表中的每个结点呢?
其实是不用的,因为这里的查询代码,可以使用跳表结点中的level数组来加速查询。
事实上,当查询一个结点时,跳表会先从头结点的最高层开始,查找下一个结点。而由于跳表结点同时保存了元素和权重,所以跳表在比较结点时,相应地有两个判断条件:
但是,当上述两个条件都不满足时,跳表就会用到当前查找到的结点的level数组了。跳表会使用当前结点level数组里的下一层指针,然后沿着下一层指针继续查找,这就相当于跳到了下一层接着查找。
这部分的代码逻辑如下所示,因为在跳表中进行查找、插入、更新或删除操作时,都需要用到查询的功能,你可以重点了解下。
//获取跳表的表头
x = zsl->header;
//从最大层数开始逐一遍历
for (i = zsl->level-1; i >= 0; i--) {
...
while (x->level[i].forward && (x->level[i].forward->score < score || (x->level[i].forward->score == score
&& sdscmp(x->level[i].forward->ele,ele) < 0))) {
...
x = x->level[i].forward;
}
...
}
这样一来,有了level数组之后,一个跳表结点就可以在多层上被访问到了。而一个结点的level数组的层数也就决定了,该结点可以在几层上被访问到。
所以,当我们要决定结点层数时,实际上是要决定level数组具体有几层。
一种设计方法是,让每一层上的结点数约是下一层上结点数的一半,就像下面这张图展示的。第0层上的结点数是7,第1层上的结点数是3,约是第0层上结点数的一半。而第2层上的结点就33一个,约是第1层结点数的一半。
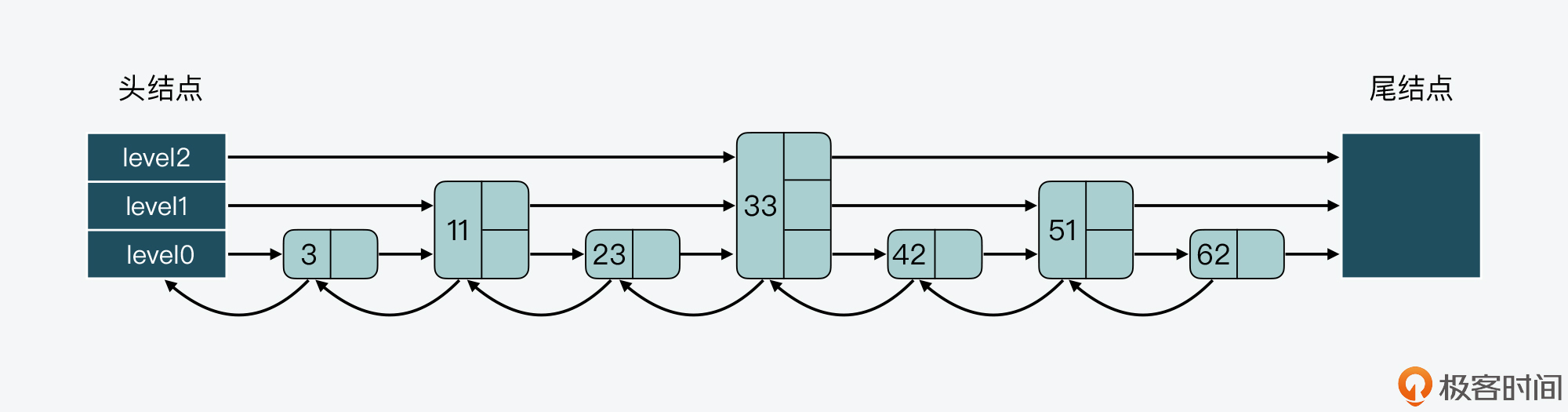
这种设计方法带来的好处是,当跳表从最高层开始进行查找时,由于每一层结点数都约是下一层结点数的一半,这种查找过程就类似于二分查找,查找复杂度可以降低到O(logN)。
但这种设计方法也会带来负面影响,那就是为了维持相邻两层上结点数的比例为2:1,一旦有新的结点插入或是有结点被删除,那么插入或删除处的结点,及其后续结点的层数都需要进行调整,而这样就带来了额外的开销。
我先来给你举个例子,看下不维持结点数比例的影响,这样虽然可以不调整层数,但是会增加查询复杂度。
首先,假设当前跳表有3个结点,其数值分别是3、11、23,如下图所示。
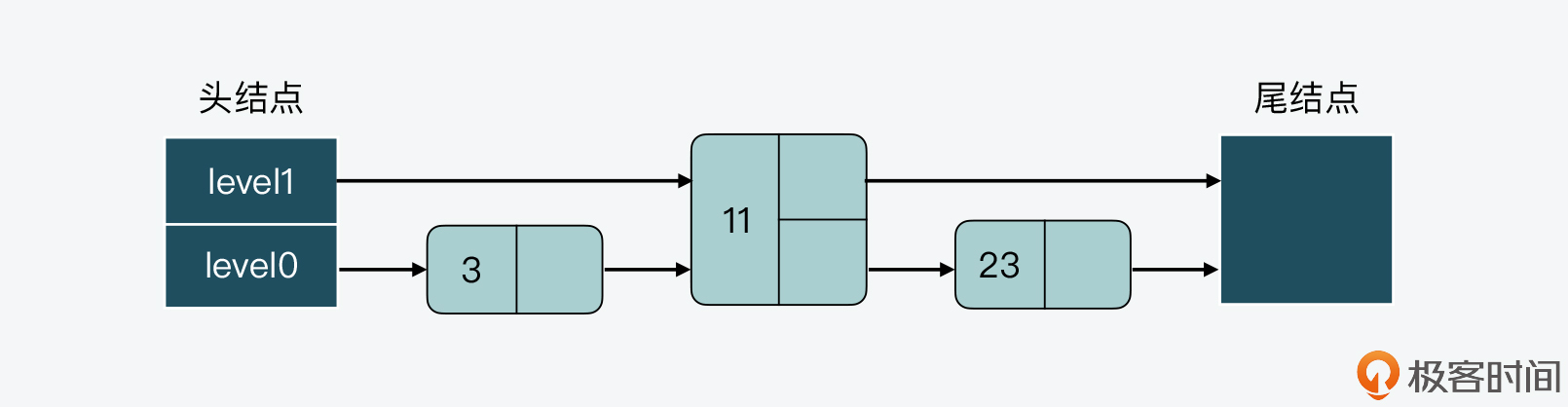
接着,假设现在要插入一个结点15,如果我们不调整其他结点的层数,而是直接插入结点15的话,那么插入后,跳表level 0和level 1两层上的结点数比例就变成了为4:1,如下图所示。
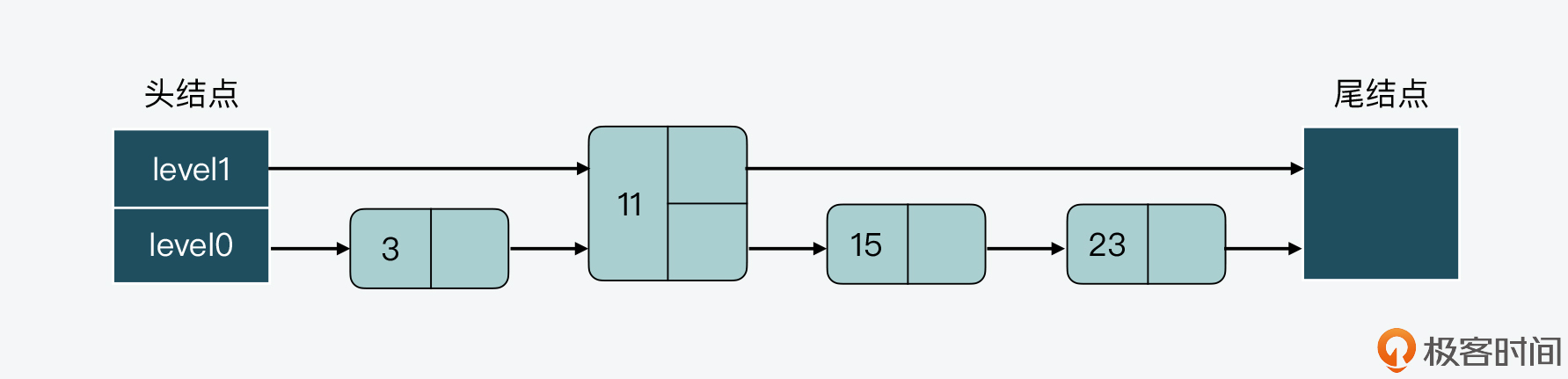
而假设我们持续插入多个结点,但是仍然不调整其他结点的层数,这样一来,level0上的结点数就会越来越多,如下图所示。
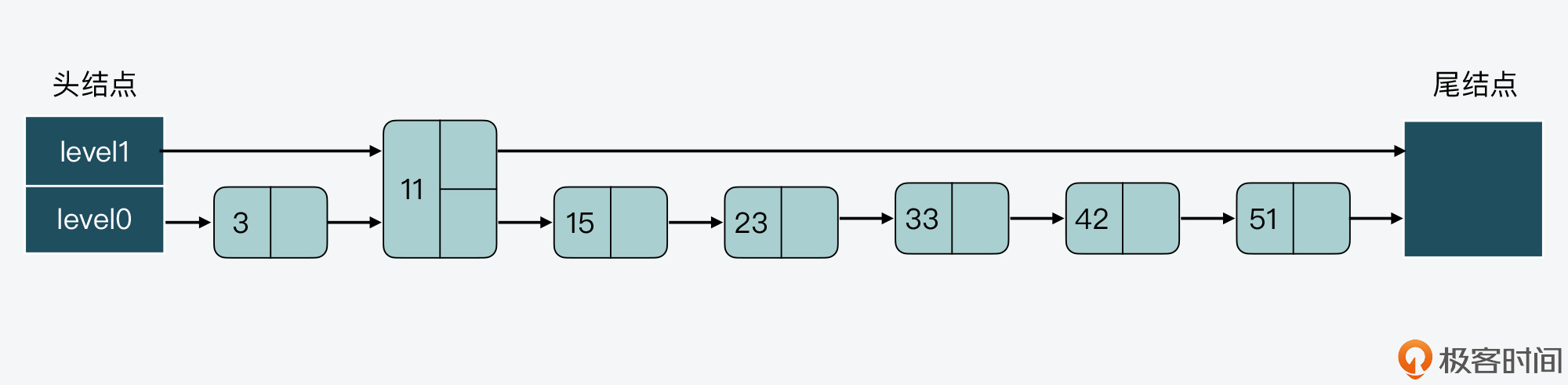
相应的,如果我们要查找大于11的结点,就需要在level 0的结点中依次顺序查找,复杂度就是O(N)了。所以,为了降低查询复杂度,我们就需要维持相邻层结点数间的关系。
好,接下来,我们再来看下维持相邻层结点数为2:1时的影响。
比如,我们可以把结点23的level数组中增加一层指针,如下图所示。这样一来,level 0和level 1上的结点数就维持在了2:1。但相应的代价就是,我们也需要给level数组重新分配空间,以便增加一层指针。
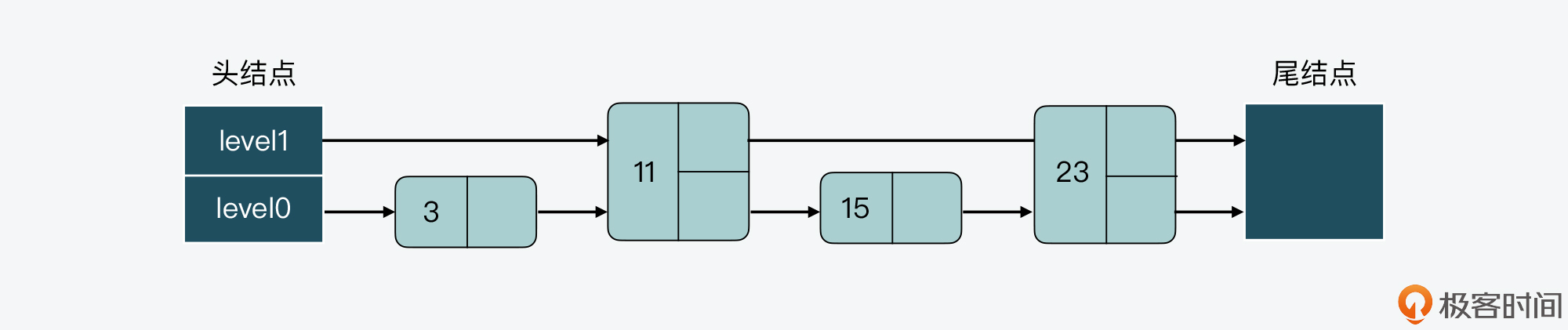
类似的,如果我们要在有7个结点的跳表中删除结点33,那么结点33后面的所有结点都要进行调整:
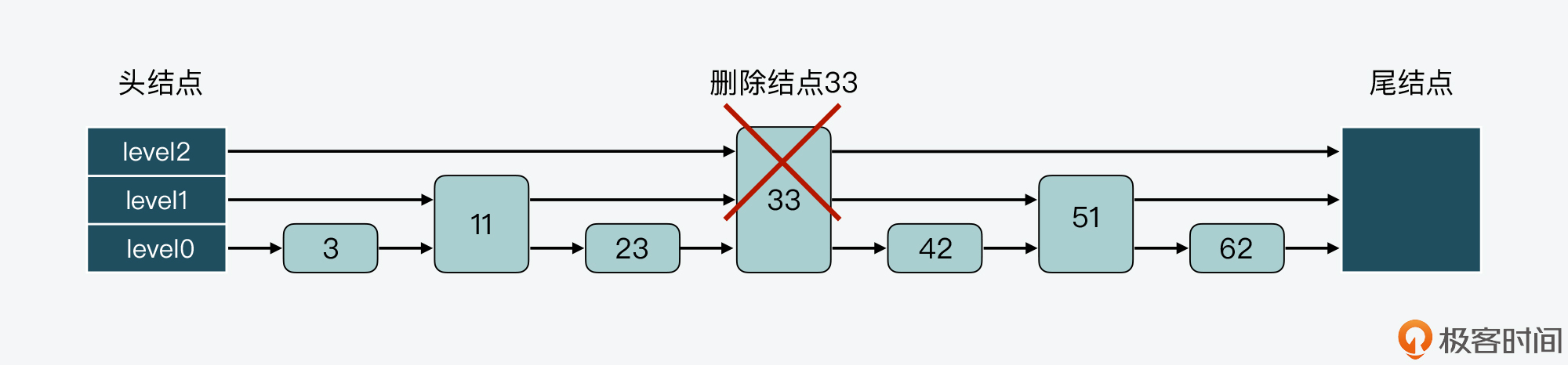
调整后的跳表如下图所示。你可以看到,结点42和62都要新增level数组空间,这样能分别保存3层的指针和2层的指针,而结点51的level数组则需要减少一层。也就是说,这样的调整会带来额外的操作开销。
因此,为了避免上述问题,跳表在创建结点时,采用的是另一种设计方法,即随机生成每个结点的层数。此时,相邻两层链表上的结点数并不需要维持在严格的2:1关系。这样一来,当新插入一个结点时,只需要修改前后结点的指针,而其他结点的层数就不需要随之改变了,这就降低了插入操作的复杂度。
在Redis源码中,跳表结点层数是由zslRandomLevel函数决定。zslRandomLevel函数会把层数初始化为1,这也是结点的最小层数。然后,该函数会生成随机数,如果随机数的值小于ZSKIPLIST_P(指跳表结点增加层数的概率,值为0.25),那么层数就增加1层。因为随机数取值到[0,0.25)范围内的概率不超过25%,所以这也就表明了,每增加一层的概率不超过25%。下面的代码展示了zslRandomLevel函数的执行逻辑,你可以看下。
#define ZSKIPLIST_MAXLEVEL 64 //最大层数为64
#define ZSKIPLIST_P 0.25 //随机数的值为0.25
int zslRandomLevel(void) {
//初始化层为1
int level = 1;
while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}
好,现在我们就了解了跳表的基本结构、查询方式和结点层数设置方法,那么下面我们接着来学习下,Sorted Set中是如何将跳表和哈希表组合起来使用的,以及是如何保持这两个索引结构中的数据是一致的。
其实,哈希表和跳表的组合使用并不复杂。
首先,我们从刚才介绍的Sorted Set结构体中可以看到,Sorted Set中已经同时包含了这两种索引结构,这就是组合使用两者的第一步。然后,我们还可以在Sorted Set的创建代码(t_zset.c文件)中,进一步看到跳表和哈希表被相继创建。
当创建一个zset时,代码中会相继调用dictCreate函数创建zset中的哈希表,以及调用zslCreate函数创建跳表,如下所示。
zs = zmalloc(sizeof(*zs));
zs->dict = dictCreate(&zsetDictType,NULL);
zs->zsl = zslCreate();
这样,在Sorted Set中同时有了这两个索引结构以后,接下来,我们要想组合使用它们,就需要保持这两个索引结构中的数据一致了。简单来说,这就需要我们在往跳表中插入数据时,同时也向哈希表中插入数据。
而这种保持两个索引结构一致的做法其实也不难,当往Sorted Set中插入数据时,zsetAdd函数就会被调用。所以,我们可以通过阅读Sorted Set的元素添加函数zsetAdd了解到。下面我们就来分析一下zsetAdd函数的执行过程。
注意,在不同编码方式下,zsetAdd函数的执行逻辑也有所区别。这一讲我们重点关注的是skiplist的编码方式,所以接下来,我们就主要来看看当采用skiplist编码方式时,zsetAdd函数的逻辑是什么样的。
zsetAdd函数会先使用哈希表的dictFind函数,查找要插入的元素是否存在。如果不存在,就直接调用跳表元素插入函数zslInsert和哈希表元素插入函数dictAdd,将新元素分别插入到跳表和哈希表中。
这里你需要注意的是,Redis并没有把哈希表的操作嵌入到跳表本身的操作函数中,而是在zsetAdd函数中依次执行以上两个函数。这样设计的好处是保持了跳表和哈希表两者操作的独立性。
如果权重值发生了变化,zsetAdd函数就会调用zslUpdateScore函数,更新跳表中的元素权重值。紧接着,zsetAdd函数会把哈希表中该元素(对应哈希表中的key)的value指向跳表结点中的权重值,这样一来,哈希表中元素的权重值就可以保持最新值了。
下面的代码显示了zsetAdd函数的执行流程,你可以看下。
//如果采用ziplist编码方式时,zsetAdd函数的处理逻辑
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
...
}
//如果采用skiplist编码方式时,zsetAdd函数的处理逻辑
else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) {
zset *zs = zobj->ptr;
zskiplistNode *znode;
dictEntry *de;
//从哈希表中查询新增元素
de = dictFind(zs->dict,ele);
//如果能查询到该元素
if (de != NULL) {
/* NX? Return, same element already exists. */
if (nx) {
*flags |= ZADD_NOP;
return 1;
}
//从哈希表中查询元素的权重
curscore = *(double*)dictGetVal(de);
//如果要更新元素权重值
if (incr) {
//更新权重值
...
}
//如果权重发生变化了
if (score != curscore) {
//更新跳表结点
znode = zslUpdateScore(zs->zsl,curscore,ele,score);
//让哈希表元素的值指向跳表结点的权重
dictGetVal(de) = &znode->score;
...
}
return 1;
}
//如果新元素不存在
else if (!xx) {
ele = sdsdup(ele);
//新插入跳表结点
znode = zslInsert(zs->zsl,score,ele);
//新插入哈希表元素
serverAssert(dictAdd(zs->dict,ele,&znode->score) == DICT_OK);
...
return 1;
}
..
总之,你可以记住的是,Sorted Set先是通过在它的数据结构中同时定义了跳表和哈希表,来实现同时使用这两种索引结构。然后,Sorted Set在执行数据插入或是数据更新的过程中,会依次在跳表和哈希表中插入或更新相应的数据,从而保证了跳表和哈希表中记录的信息一致。
这样一来,Sorted Set既可以使用跳表支持数据的范围查询,还能使用哈希表支持根据元素直接查询它的权重。
这节课,我给你介绍了Sorted Set数据类型的底层实现。Sorted Set为了能同时支持按照权重的范围查询,以及针对元素权重的单点查询,在底层数据结构上设计了组合使用跳表和哈希表的方法。
跳表是一个多层的有序链表,在跳表中进行查询操作时,查询代码可以从最高层开始查询。层数越高,结点数越少,同时高层结点的跨度会比较大。因此,在高层查询结点时,查询一个结点可能就已经查到了链表的中间位置了。
这样一来,跳表就会先查高层,如果高层直接查到了等于待查元素的结点,那么就可以直接返回。如果查到第一个大于待查元素的结点后,就转向下一层查询。下层上的结点数多于上层,所以这样可以在更多的结点中进一步查找待查元素是否存在。
跳表的这种设计方法就可以节省查询开销,同时,跳表设计采用随机的方法来确定每个结点的层数,这样就可以避免新增结点时,引起结点连锁更新问题。
此外,Sorted Set中还将元素保存在了哈希表中,作为哈希表的key,同时将value指向元素在跳表中的权重。使用了哈希表后,Sorted Set可以通过哈希计算直接查找到某个元素及其权重值,相较于通过跳表查找单个元素,使用哈希表就有效提升了查询效率。
总之,组合使用两种索引结构来对数据进行管理,比如Sorted Set中组合使用跳表和哈希表,这是一个很好的设计思路,希望你也能应用在日常的系统开发中。
在使用跳表和哈希表相结合的双索引机制时,在获得高效范围查询和单点查询的同时,你能想到这种双索引机制有哪些不足之处吗?
评论